加權回歸及權函數的變換在生物量建模中的應用

鄭 春 茂

（國家林業局華東林業調查規劃設計院 浙江杭州 310019）

1 加權回歸的概念

假定隨機變量y與x滿足下列模型：

式中：y為應變量；x位自變量；ε表示回歸模型的誤差項。采用普通回歸建立模型的先決條件，誤差項ε必須滿足“零數學期望、獨立、等方差”3個基本假設，才能獲得模型的最優估計。而誤差項的方差經常會隨著自變量的變化，產生規律性的增加或減少，回歸模型不滿足“等方差”的條件，也就是回歸模型存在異方差性，就不能獲得最優估計。

為解決誤差項ε的異方差性問題，應設法校正原有的模型，使校正后的模型其誤差項具有常數方差，而模型的校正取決于方差與自變量xi之間的關系。假設 εi的方差與xi的函數呈比例關系，即：

這里2σ 是一個有限常數。于是用去除原有模型，可使新模型的誤差項具有常數方差。用這種變換后的模型進行回歸估計，即為加權最小二乘法，簡稱加權回歸。

2 權函數的變換

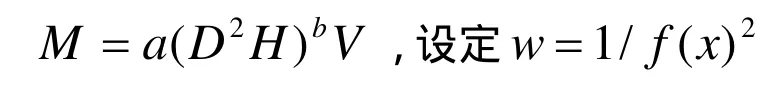
明確了權函數的結構式以后，需要將生物量模型進行變換，要求模型變換后實現系統誤差（σ）最小，使用表達式描述為：

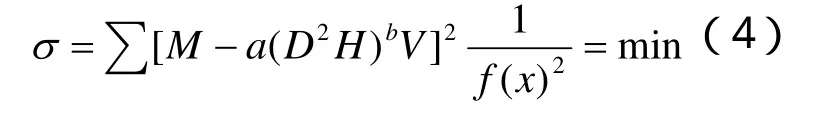
上式可以化為：

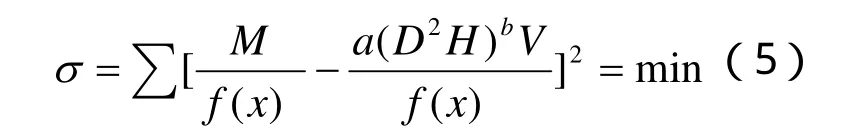
從（5）式可以看出，系統誤差最小的理想情況為：

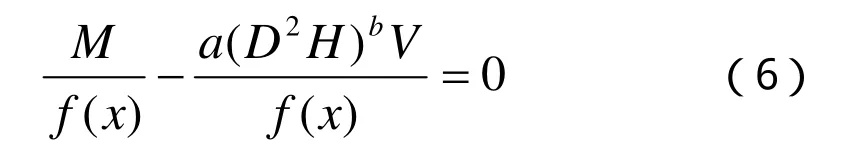
也就是滿足下面表達式為最佳：

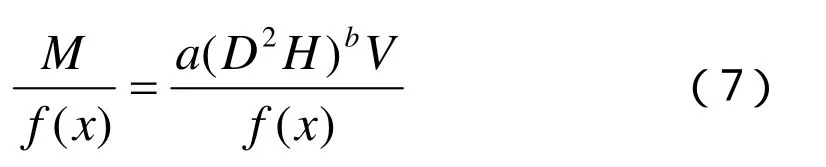
其中，f(x)為普通回歸的擬合值；M為樣本觀察值；D為胸徑；H 為樹高；V為材積。

3 實例分析

生物量建模數據，按樣本的部位可以分解為樹干、樹枝、樹葉和樹根，要求各部位單獨建立回歸模型，樣本樹枝的生物量因生長環境的不同，差異明顯，使用普通回歸的擬合結果存在異方差性，故選取2010年櫟類樹枝樣本數據，采用加權回歸估計，并對估計結果進行分析和對比。普通回歸和加權回歸擬合過程使用中國林業科學院編制的軟件ForStat 2.0版。

3.1 回歸結果

實際用于生物量建模的櫟類樹枝樣本數量n=145，自由度p=3，使用回歸模型結構式為：

其中，M表示生物量、D為樣本胸徑、H 為樹高、V為材積。

普通回歸的擬合結果如下：

附表一 普通回歸擬合結果表

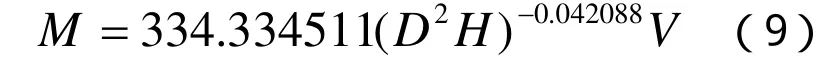
按普通回歸擬合結果建立的回歸方程，可以計算櫟類樹枝生物量的擬合值由此可以建立櫟類樹枝的回歸方程：，再將生物量觀察值與擬合值相除，其結果作為加權回歸的觀察值：

根據權函數的變換方法，可以將回歸模型結構式調整為：

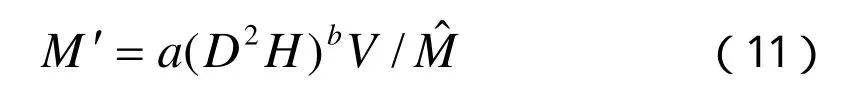
按此模型結構式進行回歸計算，得到加權回歸擬合結果：

附表二 加權回歸擬合結果表

加權回歸參數應用于普通回歸方程，建立櫟類樹枝的加權回歸方程：

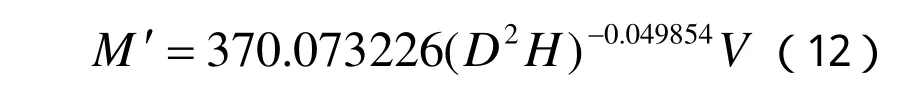
3.2 回歸模型指標評價

有許多指標對回歸模型的擬合結果進行評價，現選擇總相對誤差、總系統誤差、平均相對誤差、預估誤差、復相關系數等作為評價指標，對普通回歸和加權回歸的擬合結果進行分析對比，計算公式如下：

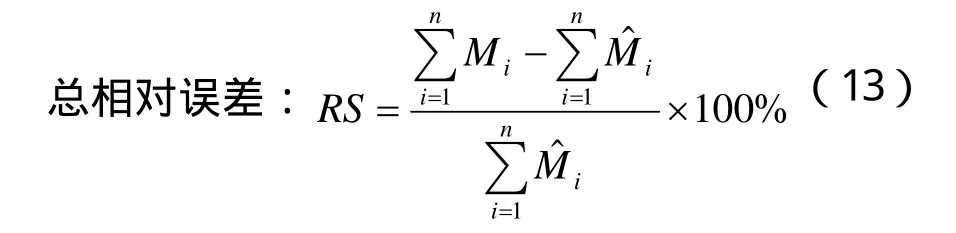
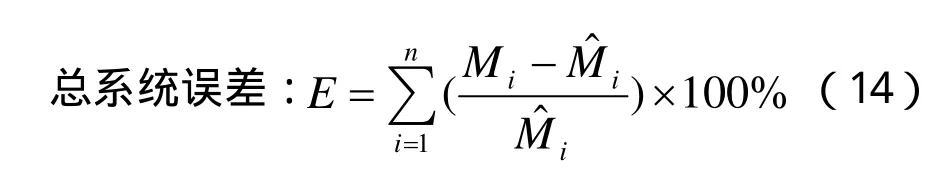
平均相對誤差：

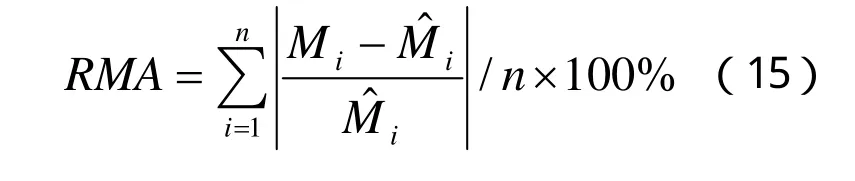
預估誤差：

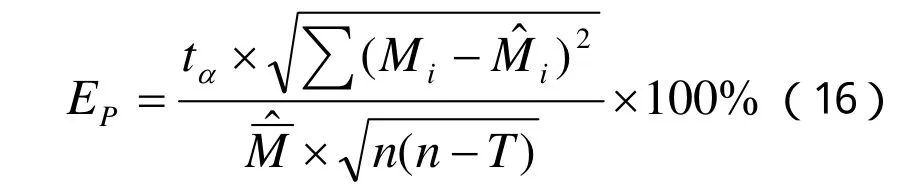
復相關系數：

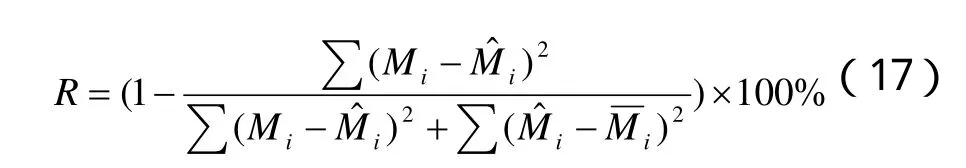
各項指標具體的計算結果如下：

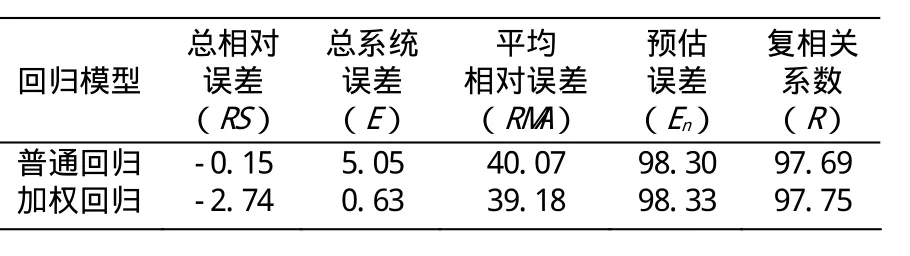
附表三 回歸模型評價指標

從表中分析，采用加權回歸，擬合結果的總相對誤差、總系統誤差、平均相對誤差指標不同程度下降，而預估誤差、復相關系數等指標有所提高，說明使用模型本身構造權函數對模型的變換，不僅消除了普通回歸存在的異方差性，同時可以提高模型擬合結果的質量。

[1] 唐守正.多元統計分析方法.北京：中國林業出版社,1984.

[2] 張會儒，唐守正，胥輝.關于生物量模型中異方差問題.林業資源管理，1999，01.

[3] 曾偉生，駱期邦，賀東.論加權回歸與建模.林業科學,1999，35.