低密度奇偶校驗碼構造及編譯碼研究進展

張用宇,吳東偉,左麗芬,劉 冰

(解放軍91469 部隊,北京100841)

1 引 言

回顧60 多年來編碼領域的發展,低密度奇偶校驗(Low-Density Parity-Check,LDPC)碼和Turbo 碼是到目前為止在糾錯編碼領域中最具代表性的成果。LDPC 碼是繼Turbo 碼之后的又一重大進展,也是目前距離Shannon 限最近的糾錯碼,是當今信道編碼領域的研究熱點之一。

1962 年,Gallager 在其博士論文中首次提出了LDPC 碼[1],并在論文中提出了兩種遞歸概率譯碼算法,但是由于當時計算機運算能力水平的限制,未能證明其具有接近Shannon 限的能力。Gallager 提出了兩個具有創造性的觀點[1]:一是用簡單稀疏校驗矩陣的隨機置換和級聯來模擬隨機碼;二是采用迭代譯碼的方法逼近最大似然譯碼。由于當時RS 碼和卷積碼的級聯被認為非常適于實際的差錯控制系統,致使Gallager 的工作被忽視了近30 年,在此期間,Zyablov、Pinsker、Margulis 以及Tanner 仍然還致力于LDPC 碼的研究。直到Turbo 碼提出以后,人們才發現Turbo 碼實質上就是LDPC 碼的一個特例,LDPC 碼又重新燃起了人們的興趣。1996 年,Mackay 等人的研究使LDPC 碼的研究跨入了一個新階段[2],他指出LDPC 碼可以像Turbo 碼一樣接近Shannon限。2001 年,Sae -Young Chung 將密度演化算法進行簡化,提出一種高斯近似(Gaussian Approximation,GA)的近似算法[3],將原來無限維的密度迭代計算轉化為一維的高斯期望計算,提高了求取LDPC 碼門限值的速度,在AWGN 信道下進行二進制傳輸,碼率為1/2 的最好不規則LDPC 碼的門限值距離Shannon 限僅僅0.004 5 dB, 仿真結果顯示, 碼長為107時,在誤比特率(Bit Error Rate,BER)為10-6的情況下,離Shannon 限的距離低于0.04 dB,這一結果超過了Turbo 碼。在近十幾年里,對LDPC 碼的研究主要集中于以下4 個方面[4]:校驗矩陣的構造、編譯碼算法的優化、性能分析和優化設計以及LDPC 碼在實際系統中的應用。本文對二進制和多進制LDPC碼的關鍵技術從構造、編碼和譯碼3 個方面進行了系統歸納和詳細探討,總結了目前已取得的最新成果,為進一步研究提供了思路。

2 校驗矩陣的構造

2.1 二進制校驗矩陣構造方法

LDPC 碼的結構決定了碼的性能,同時也決定了編譯碼方案的選擇和復雜度。LDPC 碼的校驗矩陣具有兩種形式:隨機化結構和結構化結構。到目前為止,有關LDPC 碼的構造方法數不勝數。二進制LDPC 碼校驗矩陣的構造方法主要可以分為兩大類:隨機化構造法和結構化構造法。隨機化構造法主要是按照特定的設計準則和Tanner 圖結構、度分布、停止集等條件來搜尋滿足要求校驗矩陣。典型方法主要有1962 年Gallger 提出的Gallager 構造法[1],其基本思想是第一個子矩陣采用滿足要求的固定設置,其余矩陣是第一個子矩陣的隨機列重排。1997年,Mackay 在Gallager 的基礎上給出了幾種校驗矩陣的隨機構造方法,使Tanner 圖中短環的數量最少,為了保證線性時間編碼復雜度,將校驗矩陣的構造強制為下三角陣的形式[2],但是這種約束太強,必然破壞校驗矩陣的girth 約束和變量節點及校驗節點的度數約束,從而導致性能下降。2001 年,Yongyi Mao 和Amir Banihashemi 提出一種通過girth 分布在碼字集合中尋求好碼的啟發式方法,Jorge Campello提出了具有啟發式的比特填充(Bit-Filling)算法,Xiaoyu Wu 提出了一種漸進邊增長(Progressive Edge Growth,PEG)方法[5],其在變量節點和校驗節點邊逐漸增加的過程,使Tanner 圖具有最大的girth,該方法可以產生具有線性編碼復雜度的下三角形式校驗矩陣,也可擴展到多進制LDPC 碼的構造上。結構化構造方法則是利用抽象代數、有限幾何和組合數學等數學理論構造出具有規律可循結構的校驗矩陣。在中、短碼長LDPC 碼的構造上,好的結構化構造可能會優于隨機化構造;在長碼長LDPC 碼的構造上,采用Thomas Richardson 的密度進化理論可以構造出誤碼性能很好的校驗矩陣,結構化構造校驗矩陣的性能很難與隨機構造的相媲美。但從實際角度來看,隨機化校驗矩陣缺少有規律的結構,致使LDPC碼編碼和譯碼過程變得復雜,且需要較大的存儲空間來存儲校驗矩陣,在中短碼長上隨著碼率的升高,隨機化構造法很難保證校驗矩陣的稀疏性,也難以避免Tanner 圖中的短環,構造出好LDPC 碼也就相對更難,這些缺陷都阻礙了隨機化構造的發展和應用。而結構化碼的優勢在于矩陣存儲空間小,編譯碼時延短,具有良好的最小距離和girth 特性,易于實現。2001 年,Yu Kou 提出了基于有限幾何(Finite Geometries)的LDPC 碼構造方法[6],該方法主要是利用歐氏和射影幾何中的點、線和超平面的關系,這種方法構造出的碼已經被美國國家航空航天局推薦在深空衛星通信中使用。2004 年,Bassem Ammar 提出了基于平衡不完全區組設計(Balanced Incomplete Block Design,BIBD)的LDPC 碼,BIBD 設計是組合數學中組合設計的一種方法,除此之處,相關的設計還有Steiner 和Kirkman 三 重系 統[7]、Bose 設計、反Pasch 技術等。同年,Fossorier 提出了基于循環置換矩陣的LDPC 碼構造方法,并給出了girth 為12 以下的充分必要條件或必要條件。2006 年,Lan Lan 提出了基于有限域(Finite Field)的LDPC 構造方法[8],這種方法奠定了準循環LDPC 碼構造的一種基調,后續一些學者深入研究采用不同的數學方法構造出滿足RD 約束的基矩陣。2007 年,Jun Xu 提出對LDPC碼的分解(Decomposition)和掩蔽(Masking)技術。2010 年,Jingyu Kang 提出了一種滿足RD 約束更大類構造LDPC 碼校驗矩陣的方法,其涵蓋了Lan Lan提出的有限域的第一類方法,同年,Li Zhang 對準循環校驗矩陣進行了秩分析,并給出了基于Latin 方格校驗矩陣具體秩表達式[9]。從上述的發展可以看出,Shu Lin 課題研究小組在二進制準循環LDPC 碼上的研究做出了開創和突出性的貢獻,并且其研究仍在繼續。2005 年到2008 年間,華中科技大學的彭立、朱光喜等人提出了基于等差數列、斐波那契數列、二次同余序列、Q 矩陣等LDPC 碼構造方法。2007 年,Norifumi Kamiya 提出了基于有限域仿射平面的高碼率QC LDPC 碼,并且給出了碼字的循環置換矩陣明確的秩公式,Li Zhang 對秩的分析正是來源于Kamiya 的啟示。QC LDPC 碼的構造方法層出不窮,如中國剩余定理、二次同余序列、量子理論、整數網格等,但是這些方法都是采用不同的數學方式來構造滿足RD 約束的基矩陣或是與之相關的擴展研究。

2.2 多進制校驗矩陣構造方法

二進制LDPC 碼的構造只需確定校驗矩陣中1(非零)的位置,多進制LDPC 碼的構造與二進制不同,除了位置的確定,還有數值的選取。近些年來,許多學者把目光從二進制投向到多進制上。多進制LDPC 碼的構造方法與二進制是一樣的,但為了更為明確,我們將多進制LDPC 碼的構造方法分為3 類:隨機化構造法、結構化構造法和混合構造法。這3種構造方法構造出的校驗矩陣只會具有兩種形式:隨機化結構和結構化結構,形成隨機碼和結構化碼。只有非零值的位置和取值兩個參數同時具有結構化的特性時,才認為矩陣是結構化的。多進制隨機化和結構化構造法的主要思路與二進制相同,混合構造法的主要思路是在結構化構造的基礎上融入隨機化方法,比如非零值位置的選擇采用結構化方法,數值的選取采用隨機方法,或是在結構化構造的基礎上采用隨機化方法進行處理,由此構造的碼可能是隨機碼,也可能是結構化碼。多進制LDPC 碼的構造吸取了二進制發展的經驗,大部分研究放在了結構化構造法上。2008 年,Lingqi Zeng 在二進制的基礎上提出了有限域和有限幾何的多進制QC LDPC碼構造方法[10-11]。2009 年,Bo Zhou 提出了基于有限歐氏幾何平面和陣列掩蔽(Array Masking)技術的多進制QC LDPC 碼的構造,其中采用的陣列掩蔽技術是在Jun Xu 基礎上的擴展,還提出了通過陣列分散(Array Dispersion)技術構造的多進制QC LDPC 碼,具有很好糾正突發錯誤的能力,實驗結果表明在AWGN 信道和衰落信道下,多進制QC LDPC 碼的性能明顯優于同碼長碼率的RS 碼。2010 年, Jingyu Kang 提出的滿足行距離(Row -Distance,RD)約束更大類QC LDPC 碼構造方法[12],其中包括了多進制的情況。上述方法是Shu Lin 課題研究小組在多進制LDPC 碼構造方面做出的主要工作,這些方法在繼承二進制LDPC 碼構造方法的同時,也繼承了其優缺點,有限幾何由于幾何結構的固定化,構造出的碼字數量有限,碼長碼率受限,但存在的好處在于校驗矩陣存在較多的冗余行,碼字在迭代譯碼過程中能更快地收斂;有限域法構造的具有多進制循環置換陣列結構的校驗矩陣具有較大的靈活性,輔以上述相關技術可以得到不同碼長、不同碼率、不同最小距離的規則和非規則多進制LDPC 碼。2008 年,北京理工大學劉珂珂、匡鏡明等人在滿足RD 約束要求基矩陣的框架下構造了6 種多進制QC LDPC 碼。2010年,西安電子科技大學的陳超、白寶明、王新梅等人提出了基于Singer 完備差分集構造的多進制QC LDPC 循 環碼[13],其Tanner 圖的girth 為12,最小符號Hamming 距離為6,同時也提出了基于循環最大距離可分碼的多進制QC LDPC 碼等。到目前為止,縱觀多進制QC LDPC 碼的發展,其基本思想還是停留在構造滿足RD 約束的基矩陣上,至于如何滿足,研究學者可謂各顯神通,從數學理論的各個角度設法進行挖掘研究。

2.3 girth 對校驗矩陣構造的影響

Tanner 圖中最短環的長度定義為girth。由于短環的存在會破壞變量節點和校驗節點信息傳遞的獨立性假設,使相關信息在兩類節點之間傳遞,影響碼字的迭代收斂過程。上述消除4 環的研究成果已經非常豐富,但是也有特例存在,Heng Tang 給出了存在4 環且性能優良的有限幾何LDPC 碼,定性地說明了產生的結果與多種因素有關,具體還不明確之間存在的關系。小girth 對低碼率、長度較短(103以下)的碼影響較大,消除這類碼的短環或減少其分布可以帶來明顯的性能改善,但是一味地增大girth 并不能一直提高碼字的性能。2007 年,電子科技大學的敬龍江提出了一大類基于圖形理論的無小環高度結構化的QC LDPC 碼構造方法,該方法通過設計一個有幾類特殊路徑的連接圖,來保證由此連接圖映射而得的校驗矩陣對應的Tanner 圖無小環。2009年,Xueqin Jiang 和Moon Ho Lee 提出了基于歐氏幾何兩個不同維超平面的大girth 多進制LDPC 碼構造方法,同年,也提出了基于中國剩余定理的大girth二進制QC LDPC 碼構造方法。2010 年,Morteza Esmaeili 分別提出了采用兩配置之積girth 為8 和基于兩個循環置矩陣的斜率和斜率矩陣girth 為18 的二進制QC LDPC 的構造[14]。

3 編碼設計

雖然LDPC 碼的校驗矩陣是非常稀疏的,但是其對應的生成矩陣卻并不稀疏,這使得LDPC 碼面臨著一個主要瓶頸——較高的編碼復雜度和編碼時延。目前,大部分編碼算法主要是集中在二進制LDPC 碼上,專門針對多進制LDPC 碼編碼方面的研究相對較少,對于多進制LDPC 碼編碼來說,主要思想與二進制LDPC 碼相同,只是數域和運算規則有所不同。一般來說,設計LDPC 碼編碼器存在以下4種方法。

(1)傳統的直接編碼方法

一種直接編碼方法是從生成矩陣出發,將信息位與生成矩陣相乘得到發送的碼字,其編碼的復雜度與LDPC 碼碼長的二次方成正比,而且直接編碼產生的生成矩陣過于稠密,存儲需要大量的空間;另一種是從校驗矩陣的角度出發,采用高斯消去法(加減消元法)將校驗矩陣變為下三角矩陣,進而采用遞推的方式獲得校驗位。這兩種直接方法從復雜度、時延和存儲量角度來看,完全不利于工程實現。

(2)Richardson-Urbanke(RU)方法

2001 年,由Richardson 和Urbanke 提出的基于近似下三角矩陣的編碼復雜度接近線性[15],其基本思想是利用LDPC 碼校驗矩陣的稀疏性去減小產生稠密矩陣逆矩陣的尺寸,很大程度上減輕了在編碼上巨大運算量和存儲量需求。RU 方法從校驗矩陣出發,只進行行列置換,不破壞校驗矩陣的結構,同時避開了采用非稀疏的生成矩陣對LDPC 碼進行編碼,充分利用了校驗矩陣稀疏的特點,是LDPC 碼一種通用的編碼方式,可應用于任何LDPC 碼。整體計算復雜度從O(n2)降低到了O(n +g2),其中g為校驗矩陣與近似下三角矩陣之間的“距離”。然而,RU 方法的缺點也是比較明顯的。首先,RU 方法的流水線安排不合理[16],每一級流水線復雜度不同會導致消耗的時鐘數相差比較大,降低了硬件資源的利用效率。其次,后向遞推方法在解決了下三角非稀疏矩陣與向量乘法的同時,也引入了串行的計算結構,使得目標向量中下一個分量的求解依賴于該向量之前求得的所有分量,因此后向遞推必須逐符號串行進行,大大限制了吞吐量的提升。最后,在-1沒有被強制設計為某些特殊簡單矩陣的情況下,它與向量的乘法沒有辦法做任何簡化,這使RU算法在支持自適應編碼時顯得力不從心。綜上所述,RU 算法只適合應用在碼長不太長、吞吐量要求不太高、不要求自適應編碼的場合。RU 方法只要求矩陣為非奇異稀疏矩陣,這一寬松的條件使其具有普適性,但同時也導致了該方法不會“隨機應變”,對一些特殊結構的校驗矩陣不會加以利用,可能會通過行列置換將其打亂。引入一些特殊矩陣結構可改進RU 方法,得到更為實用的編碼算法,復雜度可達到完全線性化程度,這種改進與下述構造特定的校驗矩陣實現線性化編碼的方法有交叉之處。2005年,Seho Myung 提出了一種二進制QC LDPC 碼的快速編碼方法,其校驗矩陣具有QC 形式,而且RU 算法中的 取的是單位陣,將計算校驗位的復雜度降至線性。2007 年,Sung -Eun Park 在Seho Myung 的基礎上提出了多進制QC LDPC 碼的有效編碼方法,其只是將 設計為GF(q)域下的單位陣,無需計算-1。2009 年,陳超、白寶明、王新梅提出了基于RU算法線性復雜度的多進制QC LDPC 碼有效編碼方法。RU 算法的改進是LDPC 編碼發展的一個分支方向,其編碼的方法及復雜度與碼的構造密切相關,比如塊LDPC 碼,分層近似規則LDPC 碼等都是采用RU 方法進行編碼。

(3)構造特定代數結構的校驗矩陣實現線性化編碼

特定結構中一類最重要的結構是循環或準循環結構,具有循環或準循環結構的校驗矩陣可以得到系統循環陣形式的生成矩陣,僅采用簡單的移位寄存器就可以實現線性編碼,是QC LDPC 編碼的一種有效實現方式。隨著QC 結構的流行,人們開始重新審視基于生成矩陣的編碼方法。此時的生成矩陣雖然仍是非稀疏矩陣,但是卻賦予了QC 結構的特點,只需存儲矩陣的第一行元素即可。這種QC LDPC 碼的有效編碼方法是由Zongwang Li 于2006 年提出的[17],對于串行編碼,復雜度與校驗比特的位數成正比;對于高速的并行編碼,復雜度與碼字的長度成正比。同年,Lingqi Zeng 在其博士論文中將上述二進制編碼方法擴展到多進制,實現了多進制QC LDPC 碼的高效編碼。基于QC 結構的編碼算法從系統型生成矩陣出發,計算步驟比從校驗矩陣角度出發的RU 算法顯得簡單明了。這種編碼方式可以根據實際需求控制吞吐量的大小,從串行結構到并行乃至全并行結構。由于通用的循環移位寄存器結構可以為不同的LDPC 碼所共用,因此很容易就能實現可變碼長、可變碼率的自適應LDPC 碼編碼。其不足之處在于,提升吞吐量所需要的代價是增加寄存器數量,兩者幾乎是呈線性關系的,難以滿足在有限資源下追求最大吞吐量的設計要求。除了重要的QC 結構,下面對其他一些用于有效編碼的典型校驗矩陣構造方法簡要地給予介紹。2003 年,Jin Lu提出了列重為2 的LDPC 循環碼的線性編碼方法。同年,Sarah Johnson 提出了一種采用循環碼編碼方式的準規則LDPC 碼構造方法。2006 年,Zhiyong He設計了一種具有下三角加雙對角線形式的校驗矩陣來實現線性遞推的編碼方式。2009 年,Norifumi Kamiya 提出了與循環最大距離可分碼相關的有效系統編碼方法[18],這種編碼方式的實現主要采用的循環碼的多項式乘除法電路。總之,基于特定結構校驗矩陣的LDPC 碼編碼,一類方法是從校驗矩陣的角度切入,采用遞推等方式得到校驗位;一類方法則是從生成矩陣或生成多項式的角度切入,采用反饋移位寄存器或多項式乘除法電路實現。

(4)基于迭代譯碼的編碼方法

基于迭代譯碼的編碼方法的主要原理是,把編碼過程看成是一個編碼后碼字經過二進制刪余信道(Binary Erasure Channel,BEC)后的置信傳播譯碼的恢復過程。具體來說,可認為編碼后碼字經過BEC后,所有信息位均得到保留,所有校驗位均被刪除,可以采用信度傳播譯碼算法來恢復未知的校驗位。這種迭代譯碼方式簡單,主要是由于變量節點和校驗節點之間傳遞的信息只有兩種:要么知道(概率為1)要么不知道(概率為0.5)。這種方法屬于校驗矩陣的編碼方式,不足之處在于不能保證迭代編碼能夠成功得到碼字,如果所有校驗位的節點組成的子集中存在停止集,迭代編碼很容易陷入其中。2002年,David Haley 受譯碼方式的影響,提出了LDPC 碼的迭代編碼方法,在有限的迭代次數下,采用Jacobi方法實現低復雜度編碼,而且可以與譯碼共用同一電路結構。2007 年,Mohamed Shaqfeh 和Norbert Goertz 提出了一種基于迭代譯碼的改進編碼算法,這種算法對校驗矩陣刪除相關行并添加很少的新行,以使得迭代算法不會陷入到停止集中,這種編碼復雜度是近似線性的,因為引入的新行是非稀疏的。目前,該類LDPC 碼編碼方法只應用于二進制,多進制上還未有發展。

從上述編碼方法來看,通用的方法適用范圍廣,可用于所有的LDPC 碼編碼,與碼的具體構造基本上沒有關系,其復雜度較高;而校驗矩陣具有特定結構的LDPC 碼則會充分利用其結構特性,把編碼過程的復雜度盡量降至最低,但是其可擴展性不強。

4 譯碼算法

衡量LDPC 碼譯碼方法的指標主要有:誤碼性能、計算復雜度、譯碼延遲、存儲容量,其中誤碼性能和計算復雜度是衡量的兩個最重要指標。根據實際需求的不同會有不同的LDPC 碼迭代方法,但是基本原理是相通的:在表示Tanner 圖中的變量(符號或比特)節點和校驗節點之間反復交換和更新信息。如圖1 所示,無論是二進制,還是多進制,對于LDPC碼的譯碼方法,大體可分為4 類:軟判決譯碼,該算法主要是處理接收到的符號軟信息,直接利用信道輸出的信息進行迭代譯碼;硬判決譯碼,該算法是處理接收到的符號硬判決信息,譯碼端處理的接收符號集合與發送符號集合相同,都為GF(q)(q ≥2)域中的元素,不需要信道的先驗信息;基于可靠性度量的譯碼,該算法是處理接收到符號的硬判決值,而且還要利用未作硬判決的軟信息作為可靠性度量,其目的是在少量增加硬判決算法的復雜度的前提下來提高糾錯性能,是軟判決和硬判決譯碼的折衷;混合譯碼,采用上述3 類算法中的兩種及兩種以上組合而成的譯碼算法,目的是為了在誤碼性能和計算復雜度上找到不同的權衡點。

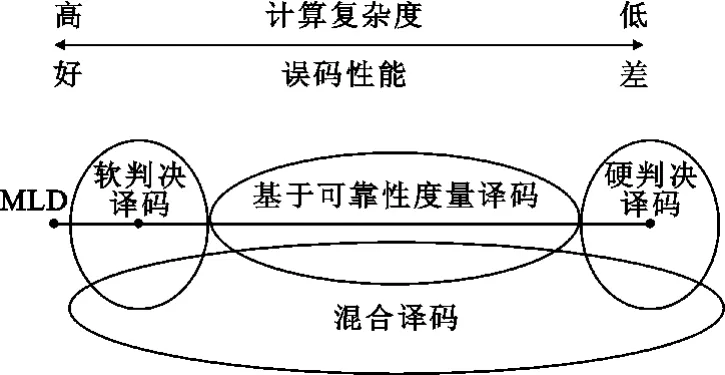
圖1 LDPC 碼的譯碼方法的分類Fig.1 Classification of decoding algorithms for LDPC codes

譯碼的任務是在已知接收碼字的條件下找出可能性最大的發送碼字作為譯碼碼字。最大似然譯碼(Maximum Likelihood Decoding,MLD)算法是在已知實際接收碼字序列的條件下使先驗概率最大的譯碼算法,該算法被認為是最好的譯碼方法,但對于LDPC碼來說,由于碼長較長,MLD 算法隨碼長呈現指數級增長導致復雜度極高而不利于實現。如圖1 所示,MLD 算法處于最高復雜度和最好性能的左端點上;軟判決譯碼是一種次最優譯碼,復雜度偏高,雖取得的性能與MLD 算法有一定差距,但卻是可實現譯碼中性能最好的譯碼方法;硬判決譯碼主要是處理接收到碼字的硬判決值,只需簡單的實數運算和邏輯運算,以犧牲性能為代價而具有很低的復雜度,適合于信道條件較好的高速通信系統;而介于軟、硬判決兩者之間的便是基于可靠性度量的譯碼。為了不同的目的而產生了兩種不同的思想,一個是從軟判決算法向下簡化,另一個是從硬判決向上優化,這兩種思想形成了兩種截然不同的發展方向,也提供了糾錯性能和算法復雜度兩者權衡的一系列滿足于不同需求的算法;而混合譯碼算法實際上是一種組合算法,其目的和基于可靠性度量譯碼一樣,而方式卻完全不同,為了得到性能和復雜度的折衷而采用兩種或兩種以上的算法,獲取兩者的優勢,削弱其劣勢,是算法的一種擴展手段。

4.1 二進制LDPC碼譯碼算法

二進制LDPC 碼可采用上述各種方式譯碼,第一個軟判決譯碼算法——概率譯碼方法是1962 年由Gallager 提出來的[1],從本質上來說,與1988 年Pearl 給出的信度傳播(Belief Propagation,BP)算法是一致的,只是兩者問題切入角度和應用環境不同罷了,前者是在LDPC 譯碼時充分利用了其他比特的相關性得到最佳后驗概率,后者是在人工智能領域用于Bayesian 網絡的消息傳遞。在Mackay、Neal、McEliece、Frey 和Kschischang 等人將信度傳播算法引入到Turbo 碼和LDPC 碼之前,廣泛應用于人工智能領域的信度傳播算法是不為信息理論學家所熟知的,其中Kschischang 證明了在因子圖上概率BP 算法或消息傳遞(Message Passing,MP)算法是和積算法(Sum-Product Algorithm,SPA)的特例,而這3 個概念在LDPC 碼譯碼中是等同的。由于概率BP 算法計算復雜,需耗費較多運算時間和硬件資源,表達形式也不夠簡潔,采用對數似然比(Log-Likelihood Ratio,LLR)后得到的LLR BP 算法誤碼性能不變,但具有更低的復雜度。從LLR BP 角度出發,多數研究學者都致力于降低復雜度而形成從LLR BP 向下簡化的軟判決算法。在LLR BP 的簡化上,Fossorier 做了大量且系統的工作,1999 年,Fossorier 提出了比特節點簡化處理的APP 譯碼算法、校驗節點簡化處理的BP-Based 譯碼算法、比特節點和校驗節點同時簡化的APP-Based 譯碼算法,這類算法有屬于軟判決譯碼的簡化算法,也有屬于基于可靠性度量的譯碼算法,但都是從LLR BP 信息的近似處理著手取得性能和復雜度的權衡,其中BP-Based 軟判決譯碼算法與Wiberg 提出的最小和算法(Min -Sum Algorithm,MSA)是同一概念。2002 年,Fossorier 研究小組中的Jinghu Chen 提出了Normalized BP-Based(或記為NMS,Normalized Min -Sum)算法和Offset BP -Based(或記為OMS,Offset M in -Sum)算法, 在原有BP-Based 譯碼算法的基礎上引入了校正因子和偏移因子,這兩種修正的譯碼算法以少量復雜度的增加取得了接近BP 譯碼算法的性能,而兩個因子參數的選取既可以通過數值仿真手段獲得,也可以通過理論推導得出。總的來說,Fossorier 的貢獻主要是對LLR BP 算法的簡化,其在校驗節點、變量節點或兩者的計算上做簡化近似或修正處理形成了一系列低復雜度的軟判決譯碼算法和基于可靠性度量的譯碼算法。譯碼算法的節點消息更新策略也是譯碼中的研究熱點之一,采用串行的方式可以比并行的方式獲得更好的性能,其主要思想是改變了變量節點和校驗節點之間全并行的消息傳遞方式,采用本次迭代中已更新的節點消息及時代替前次迭代中的節點消息參與本次更新。

第一個二進制LDPC 碼硬判決譯碼算法也是由Gallager 于1962 年提出[1]并命名為比特翻轉(Bit-Flipping,BF)譯碼算法,這種硬判決譯碼算法之后被Yu Kou 進行了改進,于2001 年提出了加權比特翻轉譯碼(Weighted Bit-Flipping,WBF)算法[6],該算法加入了比特度量信息,但卻仍保持了BF 譯碼算法低復雜度的優勢,屬基于可靠性度量譯碼。之后,許多通信學者對WBF 算法的誤碼率性能和計算復雜度加以改進。2002 年,Ahmed Nouh 提出了LDPC 碼的引導加權比特翻轉(Bootstrap WBF, BWBF)譯碼算法,在引導部分首先通過預設閾值來劃分可靠比特和不可靠比特,通過來自可靠比特的可靠校驗方程的信度傳播來重新對不可靠比特進行賦值,之后采用WBF 算法處理信息,屬混合譯碼算法,該算法在性能和復雜度上都取得了提升。2004 年, Juntan Zhang 提出了修正的加權比特翻轉(Modified WBF,MWBF)算法,該算法在WBF 的基礎上同時考慮了伴隨式的信息和每一比特自身包含的信息。F.Guo和L.Hanzo 提出了基于可靠率的加權比特翻轉(Re-liability Ratio based WBF,RRWBF)算法,其翻轉函數不需要任何的離線處理。次年,M ing Jiang 提出了改進的修正加權比特翻轉(Improved MWBF,IMWBF)算法。2005 年,Zhenyu Liu 提出了有限幾何碼的一種譯碼算法,在該算法中定義了一種新的翻轉函數,其比特選取準則綜合考慮了不滿足校驗方程的個數和接收比特的可靠性度量,并首次提出了環路檢測和規避方法,記為LP-WBF。2006 年,Inaba 和Ohtsuki提出的引導的修正加權比特翻轉(Bootstrap MWBF,BMWBF)算法不僅具有低的譯碼復雜度,而且其性能都優于WBF、MWBF 和BWBF 算法。2007 年, 吳曉富提出了并行加權比特翻轉(Parallel WBF,PWBF)算法, 在不損失性能的情況下加快了收斂速度。2009 年,吳曉富給出了不同WBF 算法和BP 算法的對偶映射關系,建立了基于可靠性度量譯碼算法和軟判決譯碼算法之間的橋梁[19]。李廣文、酆廣增提出了改進的并行加權比特翻轉算法(Improved PWBF,IPWBF),算法中融入了延遲處理方法, 將比特按照可靠性度量分為延遲處理集合和非延遲處理集合,在延遲處理集合中,只有比特輔助計數器達到某一預設閾值,才進行翻轉;而在非延遲集合中,則不需延遲直接翻轉。另一種經典的二進制LDPC 碼硬判決譯碼算法是一步大數邏輯譯碼(One -Step Majority -Logic -Decoding,OSMLD)。2009 年, Shu Lin 課題研究小組的Qin Huang 提出了基于軟可靠性度量和硬可靠性度量的兩種迭代大數邏輯譯碼算法,只需要低復雜度的邏輯運算和整數加法,其思路是從大數邏輯譯碼算法演變為基于可靠性度量的譯碼算法。

綜上所述,1962 年Gallager 給出了兩個譯碼算法發展的根節點——軟判決譯碼算法和硬判決譯碼算法。此后,Fossorier 研究小組在軟譯碼算法SPA上做了大量的簡化工作以及向下延拓了得到一些基于可靠性譯碼的算法;而Kou 則開啟了硬判決譯碼向基于可靠性譯碼算法發展的道路,引出了吳曉富、李廣文、Zhenyu Liu 和Ngatched 等人為代表在WBF算法所出的成果。如圖1 所示,二進制LDPC 碼的譯碼在各方面得到了全局性的發展,可以適用于不同通信系統LDPC 碼譯碼器的需求。

4.2 多進制LDPC碼譯碼算法

而多進制LDPC 碼譯碼器的發展不像二進制LDPC 碼發展那樣均衡,對于多進制LDPC 譯碼算法目前還處于發展研究階段,基本集中在軟判決譯碼算法方向。1998 年,Davey 和Mackay 在二進制SPA譯碼的基礎上提出了基于GF(q)(q >2)域的多進制LDPC 碼譯碼算法——QSPA,被稱為多進制經典譯碼算法,仿真表明相比于二進制LDPC 碼,Mackay法構造的列重不大于3 的多進制LDPC 碼可以在二進制對稱信道(Binary Symmetric Channel,BSC)和二進制高斯信道上取得更好的性能,這種算法導致校驗節點的計算復雜度為O(q2),正是由于這種高復雜度制約了多進制LDPC 碼的發展,因此如何降低譯碼復雜度成為多進制LDPC 碼發展的大勢所趨。在軟判決譯碼中,為減少其譯碼復雜度,對QSPA 的簡化主要從兩個分支上來進行研究:一是頻域,二是對數似然比(Log-Likelihood Ratio,LLR)域。在頻域中,2000 年,Mackay 提出了在GF(q)域上采用快速傅里葉變換(Fast Fourier Transform,FFT)的多進制譯碼算法FFT-QSPA,該算法通過FFT 轉換到頻域,從而使在校驗節點的卷積運算變成乘法運算,將計算的復雜度降低為O(q lb q),但是在FFT 和歸一化時仍需要大量的實數乘法和除法運算。2003 年,Barnault 和Declercq 采用張量表示法給出了快速譯碼算法FFT -QSPA 的實現步驟[20]。同年,Hongxin Song對FFT-QSPA 中變量節點和校驗節點的概率取對數,變乘法運算為加法運算,提出了Log -FFT-QSPA 譯碼算法,這種算法結合了傅里葉變換和對數計算的優勢,但其需要大量的對數和指數運算,不利于實用化,為了克服這個問題,可將對數和指數運算采用查找表(Look-Up Table, LUT)方式進行,但LUT的數量會隨著伽羅華域值以q lb q 的速度增長,只適合于伽羅華域元素較少的情況,同時LUT 的近似也會帶來誤碼性能的損失。在LLR 域中,2004 年,Henk Wymeersch 在二進制MS 譯碼算法的基礎上,提出了采用對數似然比的多進制LLR-QSPA,具有實現容易、復雜度低和數值穩定等特點,乘法和加法運算被加法和Jacobi 對數運算所取代,但其復雜度仍為O(q2)。2007 年,David Declercq 提出了擴展最小和(Extended Min-Sum,EMS)算法[21],為減少迭代中的復雜運算,采用LLR 域的對數似然比值作為傳遞的消息,在信度傳播校驗節點上只選取一部分(nmq)有用值來計算度量值,算法具有與FFT -QSPA近似的復雜度O(nmq),而且只有實數加法運算,沒有乘法和除法運算,復雜度大大降低, 但是相對于QSPA 譯碼而言,誤碼性能有一定的損失。受二進制BP-Based 和APP -Based 譯碼算法思想的啟發,加入校正因子和偏移因子給出了相應的修正算法。之后David Declercq 在EMS 算法的基礎上,將上述原理同時應用于校驗節點和變量節點,提出了低復雜度、低存儲容量的EMS 算法,具有O(nmlb nm)的復雜度。2008 年,北京郵電大學的周偉、全子一等人在FFT-QSPA 基礎上,提出了減小振蕩的改進算法,使每個發生振蕩的變量節點處輸出的信息包含上次信息和當前迭代后得到的信息。同年,陳昕、全子一等人提出了部分更新策略的低復雜度譯碼算法,對高可靠性的變量節點停止更新,并利用高可靠性信息進行更新的同時防止低可靠性變量節點錯誤信息的傳遞。

多進制硬判決譯碼算法2010 年才出現,其發展思路延續了二進制LDPC 碼硬判決譯碼的思路。西安電子科技大學陳超、白寶明、王新梅等人提出了多進制廣義比特翻轉(Generalized Bit Flipping,GBF)算法和修正的GBF(Modified GBF ,MGBF)算法[22],兩種算法的每一個符號都有一個整數度量值, 不同于QSPA 中傳播的實數概率值,每次迭代中對可靠的符號度量加1,最后做大數判決(或多數投票)來確定譯碼符號。GBF 和MGBF 算法的區別在于前者初始化條件直接采用了硬判決信息,而后者利用了信道軟信息值,算法都只需要有限域運算、整數加法和整數比較,屬基于可靠性度量的譯碼算法,其不足在于只針對校驗矩陣列重較大的情況。同年底,中山大學趙大源、馬嘯提出了大數邏輯可譯多進制LDPC碼的低復雜度譯碼算法[23],該算法的譯碼過程與文獻[22]提出算法一致,不同之處在于初始化選取,其采用星座圖上的歐氏距離作為初始化度量值,算法的不足之處在于只適用于大數邏輯可譯碼。Shu Lin課題研究小組的Chao-Yu Chen 提出了多進制LDPC 碼基于軟可靠性度量和硬可靠性度量的譯碼算法[24],兩種算法不同之處在于初始化信息不同,不足之處在于只適用于二進制相移鍵控(Binary Phase Shift Keying,BPSK)調制,不適用于高階調制,算法對列重很大的規則校驗矩陣更為有效。

5 結束語

本文綜述了LDPC 碼在構造、編碼和譯碼三方面的研究情況。在構造方面,主要存在隨機化和結構化兩種構造方法,目前的研究主要集中于結合代數或幾何方法的結構化構造方法;在編碼方面,考慮到編碼的復雜度,研究多集中于基于特定LDPC 碼結構的線性化編碼;在譯碼方面,衍生出了軟判決、硬判決、基于可靠性度量和混合的4 類主要算法,為減小譯碼復雜度,目前多在基于可靠性度量和混合算法上進行研究。LDPC 碼作為一種先進的編譯碼技術,是現代通信領域的研究熱點,雖然經歷了十幾年的發展歷程,但仍有很多技術有待研究,特別是多進制LDPC 碼還處在發展研究階段,有更多的未知領域亟待探索。隨著LDPC 碼的研究不斷深入下去,將為數據傳輸質量的提高提供可靠保證。

[1] Gallager R G.Low -density parity-check codes[ J] .IRE Transactions on Information Theory,1962,8(1):21-28.

[2] MacKay D J C.Good error-correcting codes based on very sparse matrices[ J] .IEEE Transactions on Information Theory,1999,45(2):399-431.

[3] Chung S, Jr Forney G D,Richardson T J,et al.On the design of low-density parity-check codes within 0.0045 dB of the Shannon lim it[ J] .IEEE Communications Letters, 2001, 5(2):58-60.

[4] Bonello N, Chen S, Hanzo L.Low -density parity-check codes and their rateless relatives[ J] .IEEE Communications Surveys &Tutorials,2011,13(1):3-26.

[5] Hu X,Eleftheriou E,Arnold D M.Regular and irregu lar p rogressive edge-grow th tanner graphs[ J] .IEEE Transactions on Information Theory,2005,51(1):386-398.

[6] Kou Y, Lin S,Fossorier M P C.Low-density parity-check codes based on finite geometries:A rediscovery and new results[ J] .IEEE Transactions on Information Theory,2001,47(7):2711-2736.

[7] Falsafain H, Esmaeili M.A new construction of structured binary regu lar LDPC codes based on Steiner systems with parameter t>2[ J] .IEEE Transactions on Communications,2012,60(1):74-80.

[8] Lan L,Zeng L,Tai Y Y, et al.Construction of quasi-cyclic LDPC codes for AWGN and binary erasure channels:A finite field approach[ J] .IEEE Transactions on Information Theory,2007, 53(7):2429-2458.

[9] Zhang L,Huang Q,Lin S, et al.Quasi-cyclic LDPC codes:An algebraic construction, rank analysis, and codes on Latin squares[ J] .IEEE Transactions on Communications,2010,58(11):3126-3139.

[10] Zeng L,Lan L,Tai Y Y,et al.Constructions of nonbinary quasi-cyclic LDPC codes:A finite field approach[J] .IEEE Transactions on Communications,2008,56(4):545-554.

[11] Zeng L, Lan L, Tai Y Y, et al.Construction of nonbinary cyclic, quasi-cyclic and regular LDPC codes:a finite geom-etry approach[ J] .IEEE Transactions on Communications,2008,56(3):378-387.

[12] Kang J, Huang Q, Zhang L, et al.Quasi-cyclic LDPC codes:An algebraic construction[ J] .IEEE Transactions on Communications,2010, 58(5):1383-1396.

[ 13] Chen C, Bai B, Wang X.Construction of nonbinary quasicyclic LDPC cycle codes based on singer perfect difference set[ J] .IEEE Communications Letters,2010,14(2):181-183.

[ 14] Esmaeili M, Gholami M.Structured quasi-cyclic LDPC codes with girth 18 and column-weight J ≥3[ J] .International Journal of Electronics and Communications,2010, 64(3):202-217.

[ 15] Richardson T J,Urbanke R L.Efficient encoding of lowdensity parity-check codes[ J] .IEEE Transactions on Information Theory,2001, 47(2):638-656.

[ 16] Zhang H,Zhu J, Shi H,et al.Layered approx-regu lar LDPC:code construction and encoder/decoder design[ J] .IEEE Transactions on Circuits and Systems I,2008,55(2):572-585.

[ 17] Li Z, Chen L, Zeng L,et al.Efficient encoding of quasicyclic low-density parity-check codes[ J] .IEEE Transactions on Communications, 2006,54(1):71-81.

[ 18] Kam iya N,Sasaki E.Efficient encoding of QC-LDPC codes related to cyclic MDS codes[ J] .IEEE Journal on Selected Areas in Communications,2009,27(6):846-854.

[ 19] Wu X, Ling C, Jiang M, et al.New insights into weighted bit-flipping decoding[ J] .IEEE Transactions on Communications, 2009, 57(8):2177-2180.

[ 20] Barnau lt L,Declercq D.Fast decoding algorithm for LDPC over GF(2q)[ C]//Proceedings of IEEE Information Theory Workshop.Paris,France:IEEE,2003:70-73.

[ 21] Declercq D,Fossorier M.Decoding algorithms for nonbinary LDPC codes over GF(q)[ J] .IEEE Transactions on Communications,2007,55(4):633-643.

[ 22] Chen C,Bai B,Wang X,et al.Nonbinary LDPC codes constructed based on a cyclic MDS code and a low-complexity nonbinary message-passing decoding algorithm[ J] .IEEE Communications Letters,2010,14(3):239-241.

[ 23] Zhao D,Ma X,Chen C,et al.A low complexity decoding algorithm for majority-logic decodable nonbinary LDPC codes[J] .IEEE Communications Letters,2010,14(11):1062-1064.

[24] Chen C,Huang Q,Chao C, et al.Two low-complexity reliability-based message -passing algorithms for decoding non-binary LDPC codes[J] .IEEE Transactions on Communications,2010,58(11):3140-3147.