有效數學作業講評及有關問題的研究

余啟友

(福建省廈門市華僑中學，福建順昌361005)

作業講評是數學教師每天必做的常規工作。常見教師在臺上講得大汗淋漓，但效果差強人意。如何讓作業講評更有效?是值得研究的問題。本學期筆者在一次作業講評時，由于未能及時解疑，從而引發全班學生課后的激烈討論，并積極參與了問題解決的探究活動。真是“不憤不啟，不悱不發”。

1 錯解展示

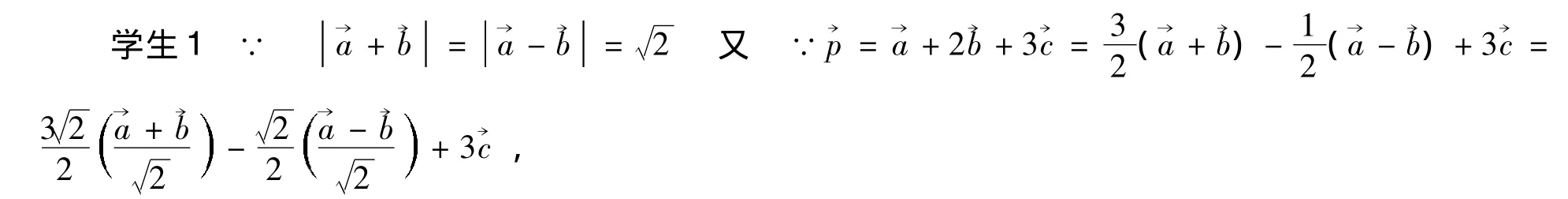
教師:誰對誰錯了呢?(學生思索中，一時回答不上)

教師:回到課本再看看定義。

學生3:我認為第二位同學是對的。因為參考答案是這么說的。原因我說不出來。

教師:究竟誰對誰錯了呢?請同學們回去查閱相關資料，下一節再討論。結果一下課，學生就分成好幾個小組在激烈爭論，并圍上來要老師評判。筆者看到學生的求知欲被激起，不愿意失去讓學生自主學習的機會。就推說自己也不知道……終于到了下一節課。

2 百家爭鳴

教師:上一節作業誰對誰錯了呢?有哪位同學已有答案了?

學生5:我查閱了高一學過的平面向量的正交分解及坐標定義:“在平面直角坐標系中，分別取與x軸、y軸方向相同的兩個單位向量作為基底。對于平面內的一個向量，由平面向量基本定理可知，有且只有一對實數x、y，使得。這樣，平面內的任一向量都可由x、y唯一確定，我們把有序數對(x，y)叫做向量的坐標，記作=(x，y)”。這里強調了表示向量的坐標必須是由單位正交基底生成的。所以我認為第一個同學是對的。

學生6:好象……不要垂直條件。請看高一必修4習題2。3B組第4題:"設Ox，Oy是平面內相交成60°角的兩條數軸分別是與x軸、y軸正方向同向的單位向量，若向量，則把有序數對(x，y)叫做向量的在坐標系中的坐標……”。

學生7:我認為垂直和單位條件都可以不要。我看了課本閱讀與思考《向量概念的推廣與應用》，并上網查了n維歐氏空間的基底與坐標定義:“若n維線性空間中任意n個線性無關的向量都可以作為線性空間的一個基。設向可由基向量組表示出，則x1，x2，…，xn稱為向量的坐標，記為(x1，x2，…，xn)”。因此我覺得向量的坐標不必是由單位正交基底生成，可以由任何基底生成的。所以第二個同學是對的。

學生8:我支持!什么是坐標?我查了現代漢語詞典坐標的定義:“能夠確定一個點在空間的位置的一個或一組數，叫做這個點的坐標”。所以我也認為第二個同學是對的。

3 水落石出

教師:同學們說得非常好，真理越辯越明。請同學們重新審題:求→在基底下的坐標。發現什么問題?(學生思索中…，突然一學生叫喊起來)

學生9:哦，我明白了!我們之前將基向量下的坐標與直角坐標系下的坐標混淆了。

教師:非常好，誰能告訴我這兩者有什么區別與聯系?

學生10:區別是:基向量下的坐標對基向量只要求不共線或不共面，而直角坐標系下的坐標必須要求基向量是單位正交基底。

學生11:聯系是:只有當基向量與坐標軸同向且是單位向量時，基向量下的坐標才等于直角坐標系下的坐標。

教師:很好，討論到現在我們可以肯定，上一節第二位同學的解答是對的。第一位同學錯在將求基向量下的坐標當成求直角坐標系下的坐標。

4 拓展練習

教師:通過今天學習，讓我們明確了:空間的一個“坐標系”可以由一個定點，三個不共面的向量，以及數乘向量和向量加法這兩個運算給出。在這樣的“坐標系”中，幾何元素及其關系不但可以得到定性刻畫，而且還能定量地表示。另外，我們可以根據面臨問題的具體條件，根據解決問題的需要(自由地)選擇“坐標系”，并且還可以在同一個平面上選擇多個“坐標系”［2］。

同時還應了解:空間點的坐標除了可以用距離來確定外，還可以用距離與角來確定。如今后將學習的極坐標、柱坐標和球坐標等。

5 教學啟示

如何有效講評數學作業呢?其實孔子在《論語·述而》中早已告訴我們:“不憤不啟，不悱不發，舉一隅，不以三隅反，則不復也。”“憤”就是學生對某一問題正在積極思考，急于解決而又尚未搞通時的矛盾心理狀態。這時教師應對學生思考問題的方法適時給以指導，以幫助學生開啟思路，這就是“啟”。“悱”是學生對某一問題已經有一段時間的思考，但尚未考慮成熟，處于想說又難以表達的另一種矛盾心理狀態。這時教師應幫助學生明確思路，弄清事物的本質屬性，然后用比較準確的語言表達出來，這就是“發”。“舉一隅，不以三隅反，則不復也。”舉出一個角為例來告訴學習的人，而他不能推斷其他三個角如何，就不用再教他了。因為他不用心思考。

數學作業講評是課堂教學的有機組成部分，是師生交流的平臺。通過數學作業講評，交流學生的學習成果，把學生作業中出現的想法、創見、存在的錯誤作為教學的資源，為矯正學生自己的學習缺陷服務，鞏固、充實、完善和強化數學知識技能，促使知識再整理、再綜合、再運用;學生通過自查錯誤，能培養自主學習能力，促進主體的自我發展;學生在辨析糾錯的過程中，能以數學概念定理為依據，修補認知上的缺陷，形成正確的認知;通過講評活動，提煉學生的思想方法及個性想法，使學生對所學知識融會貫通，培養學生的數學思維能力［3］。

［1］課程標教材研究所.數學選修2－1［M］.北京:人民教育出版社2010，10.

［2］課程標教材研究所.數學必修4教師教學用書［M］.北京:人民教育出版社，2010.

［3］任升錄，等.數學作業的設計與評價［M］.上海:人民教育出版社，2009.

［4］Paul R Burden，David M Byrd.Methods for Effective Teaching:Meeting the Needs of All Students［M］.Beijing:Pearson Education(Beijing)office，2008.

［5］Clarke D J，Keitel C，Shimizu Y.Mathematics Classrooms in Twelve Countries:The Insider’s Perspective［M］.Rotterdam:Sense Publishers，2006.