一種瞬時圓周加速度制導律設計

李偉，王志剛，蔣奇英

(1.西北工業大學航天學院，陜西 西安 710072;2.第二炮兵青州士官學校202教研室，山東 青州 262500)

引言

制導律的選擇對導彈能否精確打擊目標至關重要，而制導律的設計需要從導彈的飛行性能、作戰空域、技術措施、制導精度、制導設備、戰術使用等方面進行綜合考慮與衡量［1］。

隨著現代控制理論的發展，最優控制、滑模變結構控制、預測控制等諸多非線性控制方法也開始用于制導律設計，一些學者還研究了跟蹤某條特殊軌跡來產生制導指令的幾何曲線制導律［2］。其中最優制導律、變結構制導律、預測制導律由于制導形式過于復雜，制導參數難以選擇，不適合工程運用。幾何曲線制導律制導形式簡單，且減少對測距信息的要求，擴展了導引頭的選取范圍。

針對導彈和目標速度恒定的情況，Manchester等［3-4］根據平面彈道的幾何特性提出了一種具有終端角度約束的圓周制導律。其基本思想為:假定在每一時刻，導彈和目標的位置均處于同一個圓上，且所需的終端速度方向位于目標點的切線上(故每一時刻均可確定出唯一的圓)，因此只要控制導彈沿該圓飛行，即可命中目標。文獻［5］中將圓周加速度概念應用到三維方案彈道跟蹤，但其攻擊目標是固定的，這在實際應用中存在很大弊端。

本文依照導彈質心和目標質心相對位置關系，將文獻［6］中所提出的一種圓周加速度非線性制導律推廣到三維情況下攻擊運動目標的任務中，設計的制導律不但能夠準確命中目標，而且彈道較為平直。

1 瞬時圓周加速度制導原理

介紹瞬時圓周加速度制導原理前，需要引入一個新的坐標系——相對彈道坐標系Oxryrzr。原點O選取在導彈的質心上;Oxr軸與導彈質心相對目標質心的速度矢量vr重合;Oyr軸位于包含相對速度矢量vr的鉛垂平面內，且垂直于Oxr軸，向上為正;Ozr軸按右手定則確定。

制導原理如圖1所示。在任一瞬時，Oxr為導彈質心相對目標質心速度矢量方向;OT為目標的質心;O1為以OOT(線段r)為弦、以Oxr為外切線的圓的圓心，其半徑為R;η為垂直相對速度矢量的半徑與Ozr軸的夾角，其中OO1在Oyrzr平面內;η1為弦OOT與相對速度矢量的夾角;O2為目標質心OT在Oxrzr平面內的投影，O2O3垂直于Oxr軸。

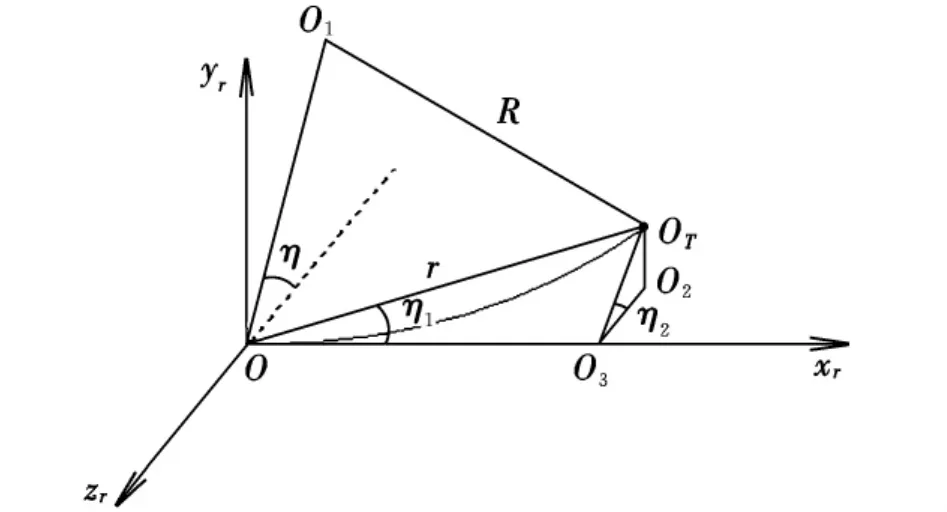
圖1 瞬時圓周加速度制導原理圖

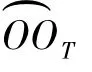
2 制導方程推導

將圖1中平面OO1OT取出放大后如圖2所示。

圖2 制導原理的幾何關系

根據圖2所示幾何關系，可得:

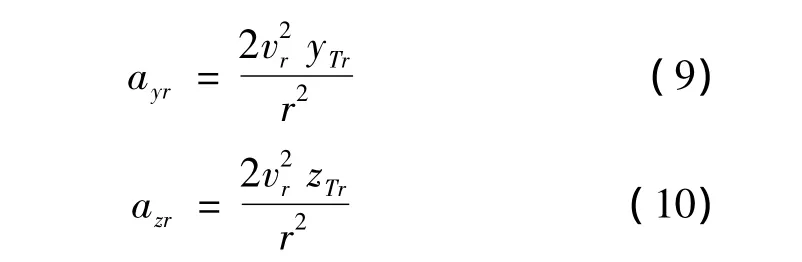
若要解算式(9)和式(10)，還需要 vr，yTr，zTr和r，其中r為彈目相對距離，可參見文獻［7］通過彈目相對運動方程求解得到。

導彈質心和目標質心相對速度的大小和相對地面坐標系的方位為:

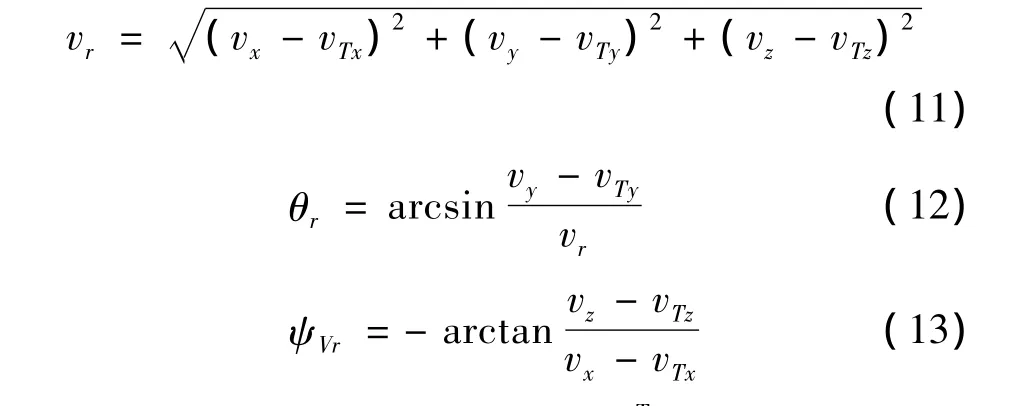
式(11)～式(13)中，［vxvyvz］T為導彈速度矢量v在地面坐標系中的分量;［vTxvTyvTz］T為目標速度矢量vT在地面坐標系中的分量。各分量的求解參見文獻［7］。

導彈質心和目標質心之間的相對位置關系如圖3所示。

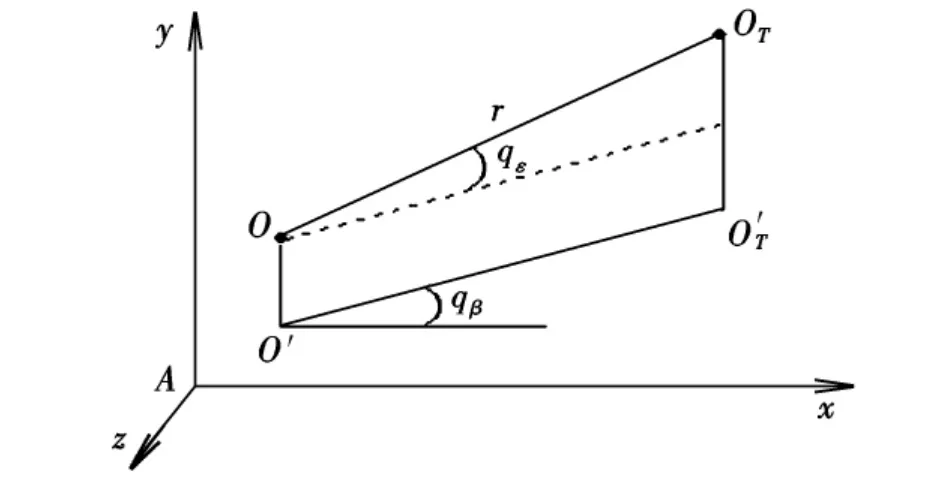
圖3 導彈和目標相對位置關系

圖3中，坐標系Axyz為地面坐標系，定義見文獻［7］，導彈和目標的相對距離在地面坐標系中的分量可由下式表示:

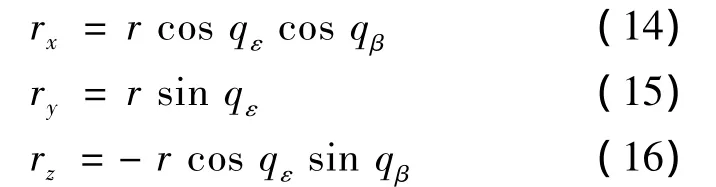
式中，qε為視線高低角;qβ為視線方位角。

彈目相對距離在相對彈道坐標系中的投影可通過地面坐標系與相對彈道坐標系之間的轉換矩陣求得，即:

式中，L(θr，ψVr)為地面坐標系和相對彈道坐標系之間的轉換矩陣，具體為:

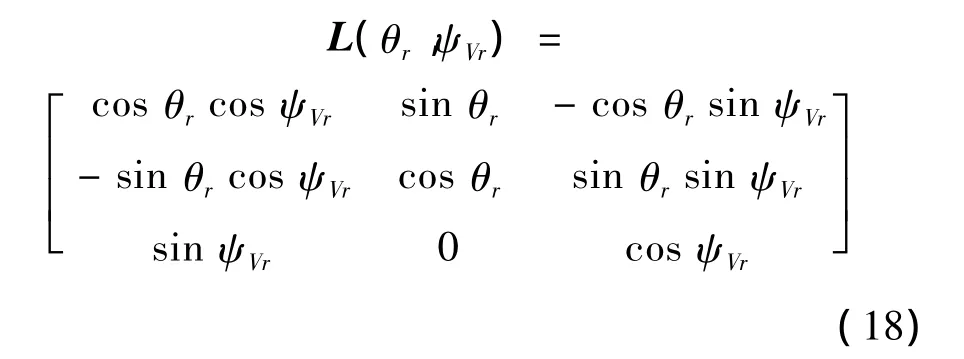
參照上述公式可以求解出在相對彈道坐標系下的加速度指令，但不能直接應用在導彈動力學方程中，需要將相對彈道坐標系中的加速度指令投影至彈道坐標系中才可以使用。因此需要做兩次坐標轉換，首先由相對坐標系轉至地面坐標系，再由地面坐標系轉至彈道坐標系，即:

3 仿真計算

假設導彈空中發射攻擊地面運動的武裝車輛。武裝車輛以勻速vT=11 m/s的速度沿著地面坐標系z軸負方向運動，武裝車輛質心的起始位置坐標為xT=3 500 m，yT=1.5 m，zT=0 m。導彈仿真初始參數如表1所示，三維彈道仿真曲線如圖4所示。

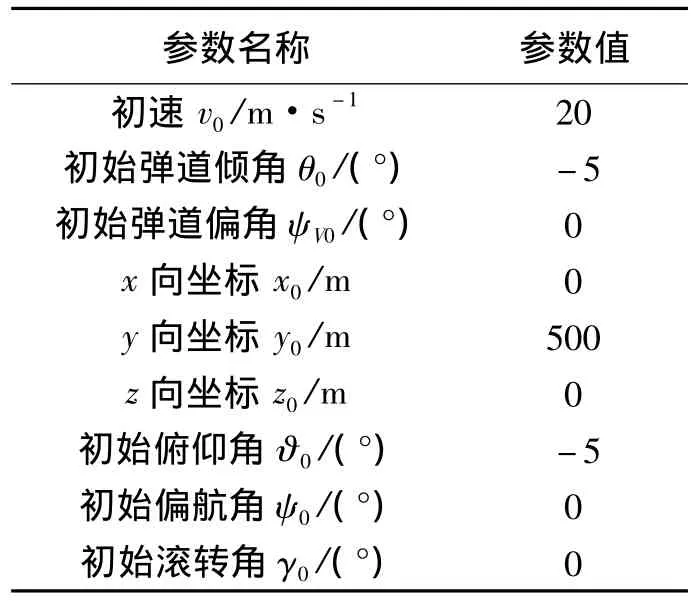
表1 導彈仿真初始參數

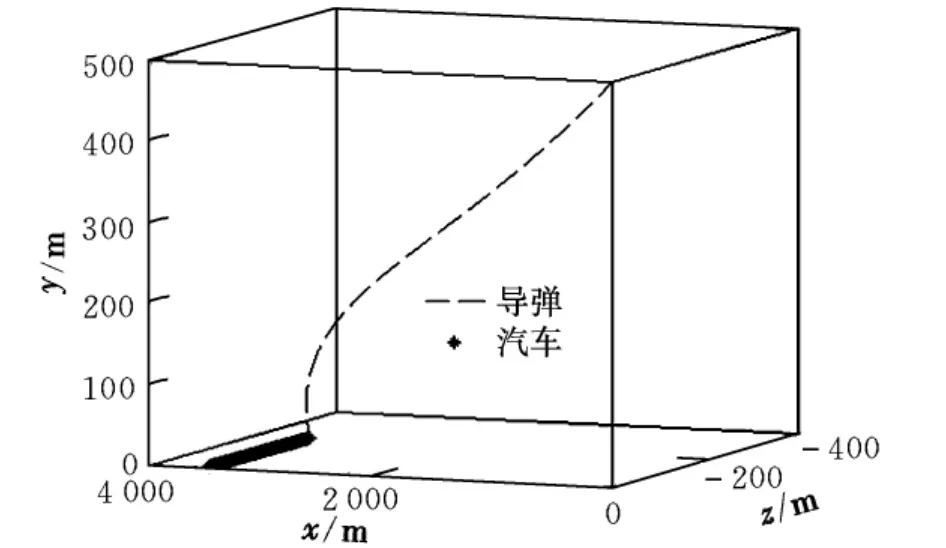
圖4 三維彈道仿真曲線圖

圖5～圖7給出了瞬時圓周加速度制導的彈道特性。在整個過程中，彈道角、姿態角和過載變化平滑，表明該制導方法可以得到較為平直的彈道。

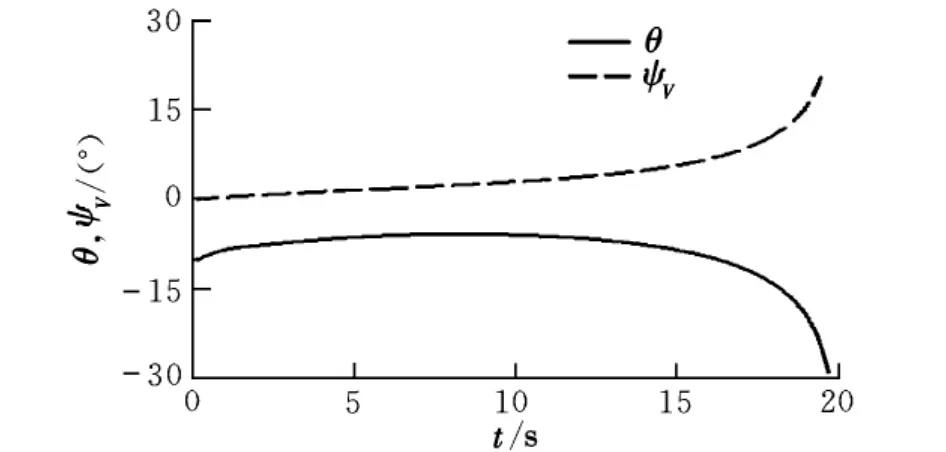
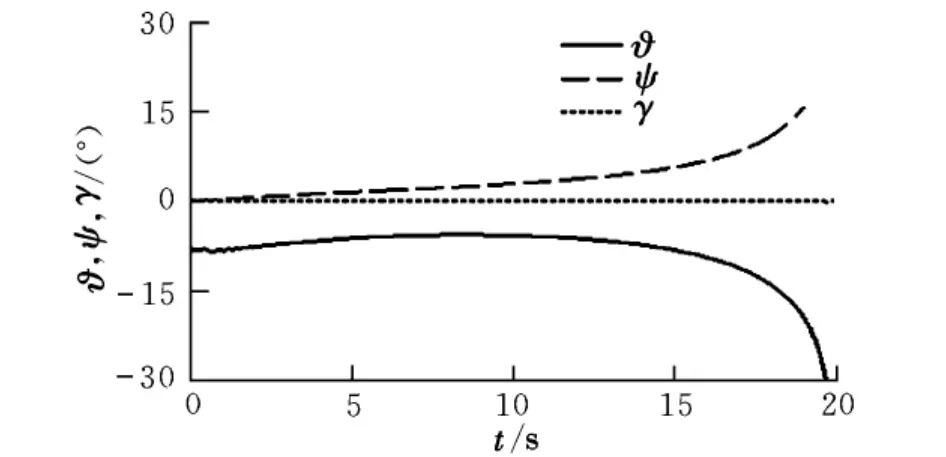
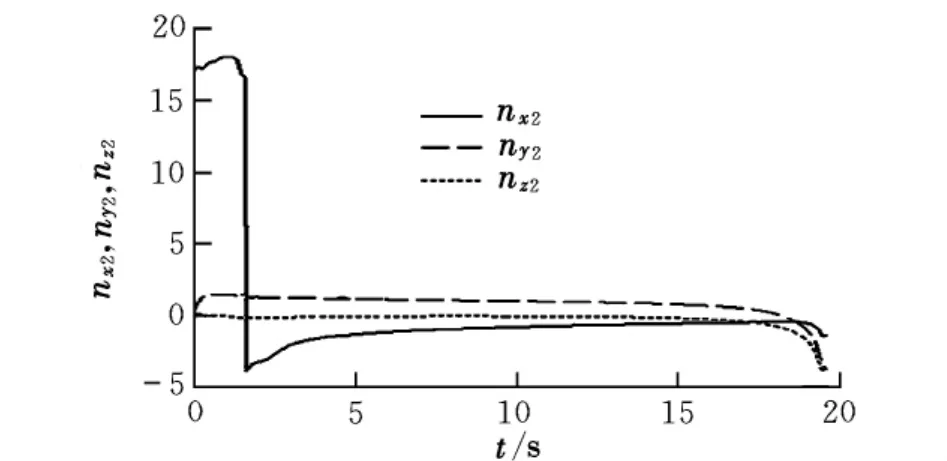
圖7 過載仿真曲線

仿真結果主要參數如表2所示。

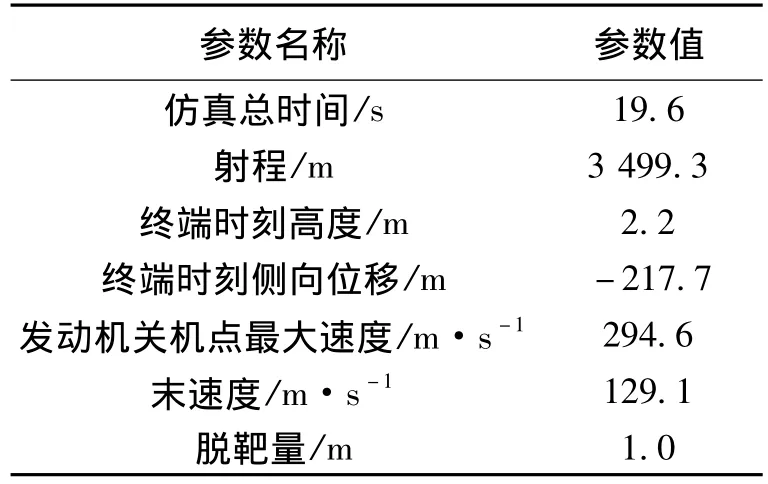
表2 仿真結果主要參數

可以看出，導彈最終命中目標，脫靶量僅為1.0 m，滿足最終精確制導的要求。

4 結束語

本文介紹了瞬時圓周加速度的制導原理，并推導了制導方程。以某型導彈為例進行了彈道仿真，結果表明所設計的制導方法在攻擊移動地面車輛時能夠準確命中目標，而且彈道較為平直，對實際的彈目追蹤問題具有一定的參考價值。

［1］ 王亞飛，方洋旺，周曉斌.比例導引律研究現狀及其發展［J］.火力與指揮控制，2007，32(10):8-12.

［2］ 蔡洪，胡正東，曹淵.具有終端角度約束的導引律綜述［J］.宇航學報，2010，31(2):315-323.

［3］ Manchester IR，Savkin A V.Circular navigation guidance law for precision missile/target engagement［C］//Proceedings of the 41st IEEE Conference on Decision and Control.Las Vegas，USA，2002.

［4］ Manchester IR，Savkin A V.Circular navigation missile guidance with incomplete information and uncertain autopilot model［J］.Journal of Guidance，2004，27(6):1078-1083.

［5］ 王旭剛，王中原，李小元.一種非線性方案彈道跟蹤算法［J］.彈道學報，2010，22(4):23-26.

［6］ Sanghyuk P，John D，Jonathan PH.A new nonlinear guidance logic for trajectory tracking［R］.AIAA-2004-4900，2004.

［7］ 李新國，方群.有翼導彈飛行力學［M］.西安:西北工業大學出版社，2004.