小衛星偏心分離動力學仿真模型的建立與驗證

沈曉鳳，肖余之，康志宇

(1.上海市空間飛行器機構重點實驗室，上海 201108;2.中國航天科技集團公司空間安全與維護總體技術研究中心，上海 201108)

引言

隨著現代航天技術的發展，小衛星由于發射方式靈活、研制成本低以及研制周期短等特點得到了廣泛應用。目前世界上已有十多個國家涉足小衛星研制領域，美國、俄羅斯、法國、英國、意大利等都有了自己的小衛星平臺或星座［1］。繼2000年美國國防高級研究計劃局(DARPA)成功以母子星方式一箭發射了五顆小衛星后，2005年俄羅斯一箭發射了九顆小衛星，其中一顆小衛星在軌釋放了三顆皮衛星。中國也十分重視小衛星及其應用的發展，2010年9月，“長征2號丁”運載火箭采用發射筒裝置成功搭載發射了浙江大學研制的兩顆“皮星1號A”衛星，通過星箭分離成功入軌。

小衛星入軌方式一般分為兩種:直接由地面運載火箭通過一箭多星技術發射入軌或者由上面級(機動平臺)搭載發射。后者由于多星釋放，必然存在偏心安裝，因此小衛星偏心分離動力學問題成為必須研究的內容。由于小衛星和分離平臺間安裝和連接方式的多樣性，不同的簡化模型和初始狀態對分離過程和最終精度有很大的影響，有時候甚至是決定性的［2］。本文以上面級平臺筒式分離機構方案為應用背景，對小衛星的偏心分離進行了動力學仿真研究。

1 偏心在軌分離模型

筒式偏心在軌分離問題可描述如下:小衛星2分離前安裝在釋放筒內部，底部作用分離彈簧，釋放筒偏心安裝在主平臺1上，其相對主平臺的安裝位置和坐標系定義如圖1所示。

圖1 偏心在軌分離模型

小衛星上分別設置了3個上支撐和3個下支撐與釋放筒上的3根導軌配合，上下支撐內部均裝有壓緊彈簧，與導軌間的壓力可根據需要進行調節，三方向設置如圖2所示。

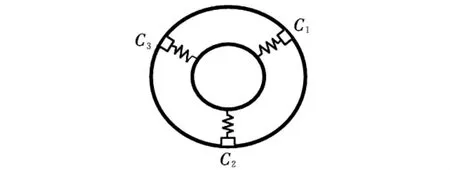
圖2 三方向支撐分布示意圖

2 筒式偏心分離動力學理論

文獻［3］提出的筒式偏心在軌分離是一類具有平移副約束的分離問題。為了更好地描述小衛星筒式偏心分離的動力學問題，本文在分離動力學建模中對文獻［3］中的簡化模型與未簡化的物理模型進行探討，分析平移副約束簡化模型，仿真該類分離動力學問題的有效性。

建立如圖1所示的坐標系，其中Oxyz為軌道慣性坐標系，O1x1y1z1為主平臺本體坐標系，O2x2y2z2為小衛星本體坐標系。建立分離動力學模型時，采用以下假設:

(1)小衛星為剛體，并將釋放筒與主平臺視為同一剛體，則分離過程可考慮為兩剛體運動過程;

(2)分析所得的轉動角度及轉動角速度均為相對分離時刻的瞬時軌道坐標系;

(3)在真空零重力條件下進行分離過程數學建模，不考慮攝動力影響［3］。

2.1 受力分析

為避免奇異點的出現，在數學模型推導過程中采用312坐標轉換順序，把握分離過程中各矢量的關系，對小衛星與主平臺進行受力分析:

式中，Fui為3個上支撐與導軌接觸力;Fdi為3個下支撐與導軌接觸力;Fs為分離彈簧力;ρ1ui，ρ1di分別為主平臺質心到上、下支撐作用點的矢徑在慣性坐標系下的投影;ρ2ui，ρ2di分別為小衛星質心到上、下支撐作用點的矢徑在慣性坐標系下的投影;ρ1s，ρ2s分別為主平臺質心、小衛星質心到分離彈簧作用點的矢徑在慣性坐標系下的投影。

2.2 接觸力模型

Khulief和Shabana基于Hertz定理與阻尼函數的運動副間隙模型，結合牛頓定理，將碰撞特性等效為無質量的線性彈簧阻尼器。在此基礎上，Lankarani和Herbert等提出了基于Hertz接觸理論和恢復系數的非線性彈簧阻尼模型［4］。

如圖3所示，將支撐活塞與導軌的接觸分析簡化為平面問題，忽略其y向厚度所帶來的影響。輔助支撐活塞與導軌的接觸包含兩種接觸方式:z向的雙面接觸和x向的單面接觸。根據接觸碰撞模型理論，采用非線性彈簧阻尼模型，利用一個三維力對支撐活塞與導軌間的接觸進行建模。將支撐活塞與導軌簡化為初始重合的兩質點，兩者x向與z向的接觸力可通過兩質點間的相對位移和相對速度來表示，y向表示為x向與z向接觸力所帶來的摩擦力。該三維力模型的力學表達式為:

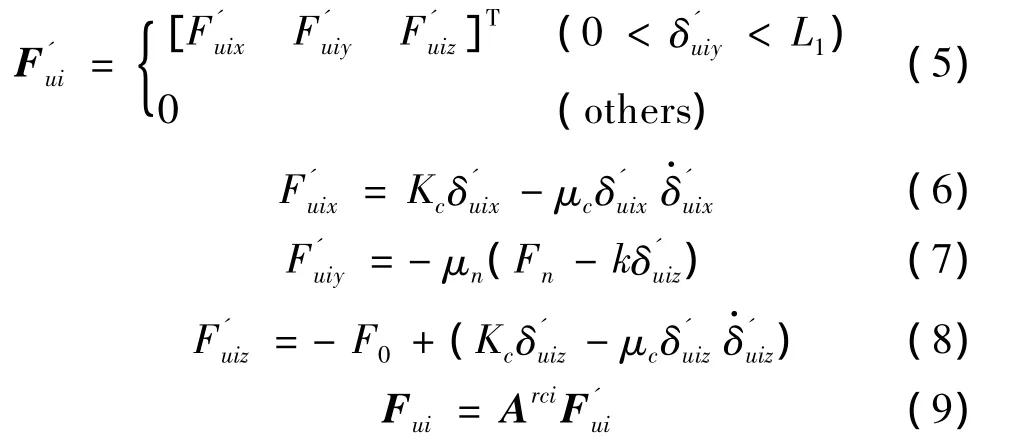
式中，Kc為等效接觸剛度;μc為阻尼系數;F0為初始預緊力。下支撐與導軌的接觸力表示同上。

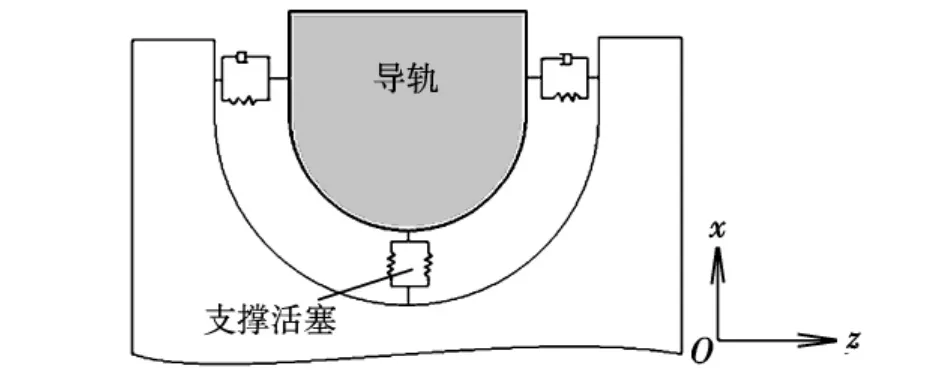
圖3 彈簧阻尼模型

2.3 牛頓歐拉方程

建立牛頓歐拉方程，通過四階龍格-庫塔法求解可得到試驗小衛星與主飛行器的分離姿態［5-6］:

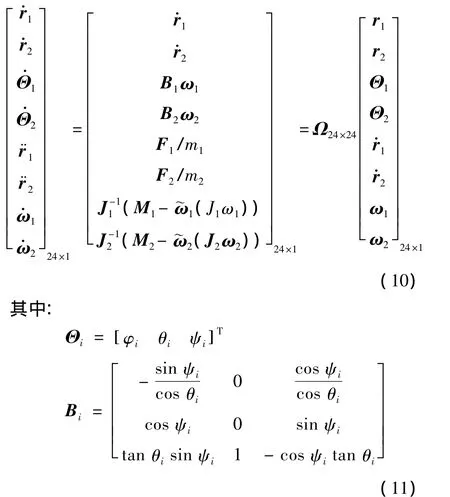
式中，i=1，2;φ，θ，ψ 分別為偏航角、滾轉角和俯仰角。值得注意的是:平動副約束簡化模型中無支撐與導軌接觸力作用，Fui和Fdi均為0，小衛星與主平臺具有相同的角速度，故滿足B1=B2。

3 算例及結果

仿真分析中，設上支撐預緊力100 N，下支撐預緊力為0 N，分離彈簧行程200 mm，分離力過質心，其中:

基于上述多體動力學理論依次對兩種模型進行仿真分析，觀察兩模型的出筒姿態規律。圖4為平動副約束模型(簡化模型)下的小衛星與主平臺分離角速度曲線，根據彈簧工作狀態可將分離過程分為彈簧分離行程與小衛星分離出筒時刻兩個階段。圖5為物理模型下兩者的分離角速度對比曲線，分離過程可簡單劃分為彈簧分離行程、上支撐出筒時刻和下支撐出筒時刻三個階段。

比較兩種模型的分離角速度曲線，其變化規律與幅值大小都存在較大差別。為了驗證數學模型的正確性，將利用地面試驗探尋筒式偏心分離小衛星的分離姿態規律。

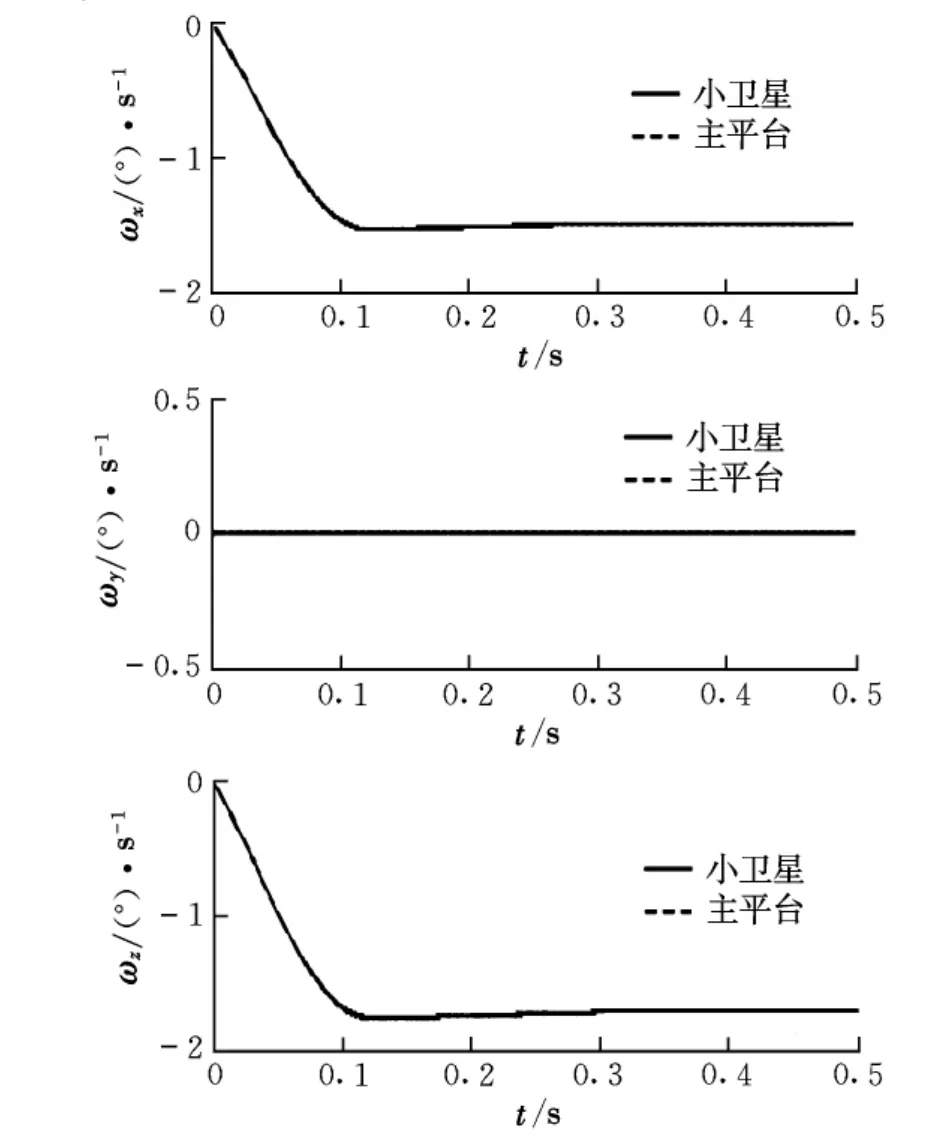
圖4 小衛星與主平臺分離角速度曲線(簡化模型)

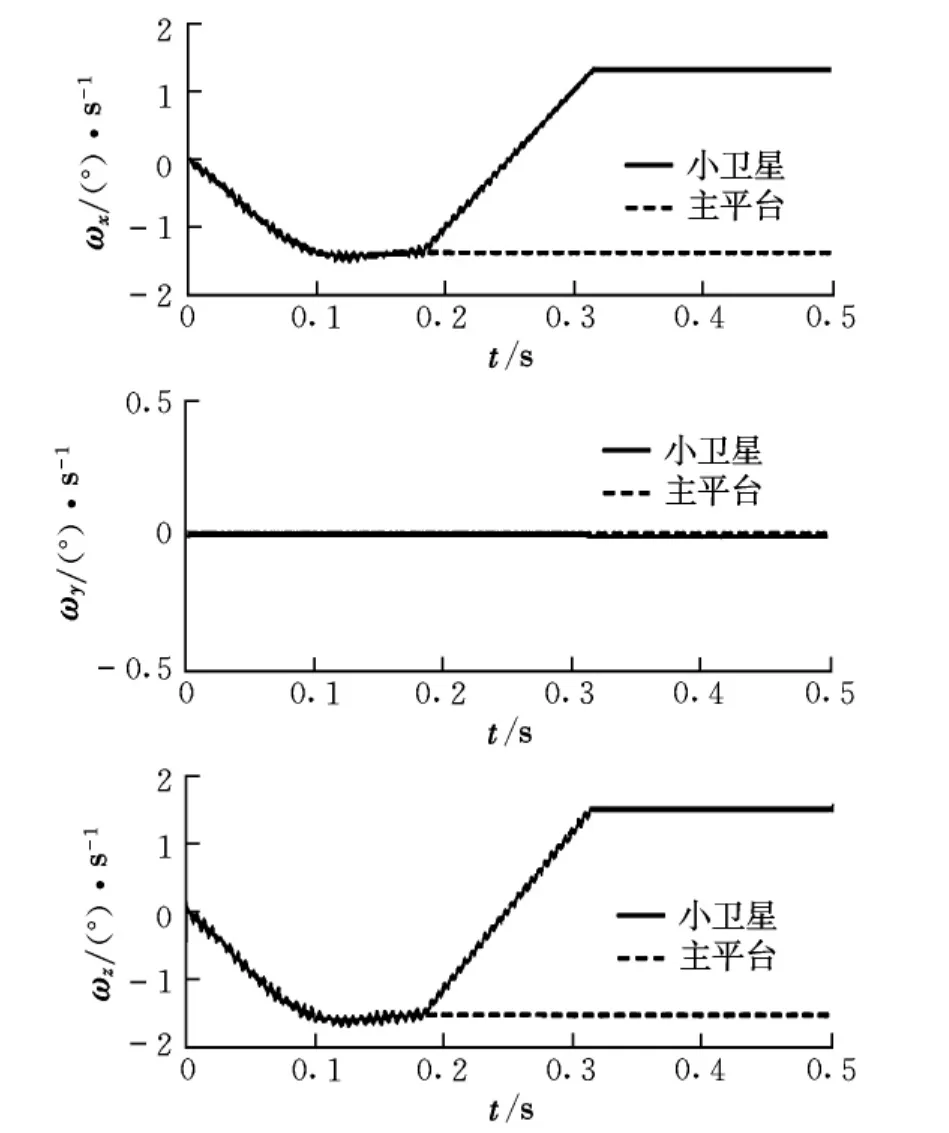
圖5 小衛星與主平臺分離角速度曲線(物理模型)

4 地面模擬試驗

地面試驗系統采用單點吊掛主平臺、依靠自由落體模擬主平臺的在軌失重狀態，在自由落體過程中完成小衛星與主平臺的解鎖分離，利用慣導測量系統測得小衛星與主平臺的位姿、速度等參數，試驗系統組成如圖6所示。綜合考慮，地面試驗分離流程采用兩步:首先釋放主平臺，小衛星跟隨主平臺自由落體運動;持續0.4 s后，偏心分離小衛星。

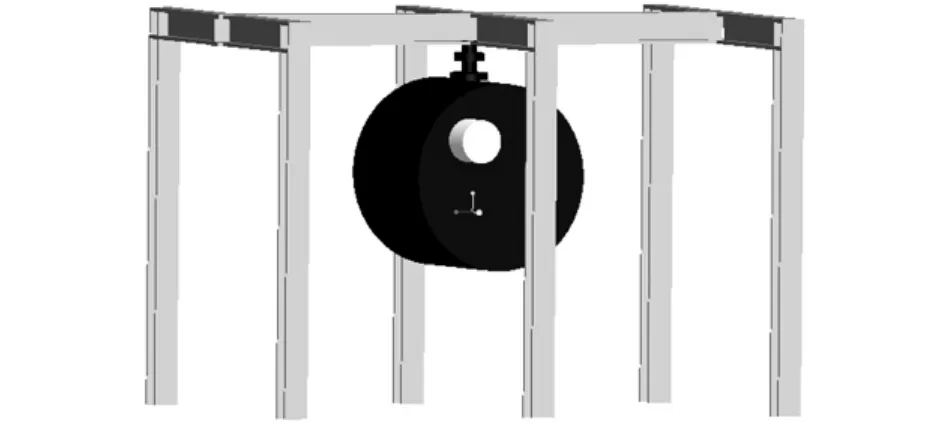
圖6 試驗系統組成

4.1 試驗系統基頻分析

在分離試驗系統中，采用設計接口與仿真模型一致，而質量、慣量略有出入的小衛星與主平臺模擬件。分析地面模擬試驗數據，發現試驗曲線存在一定的振蕩，故對其主平臺模擬件進行自由狀態的模態分析。

根據模態分析結果，除剛體模態外，主平臺前三階振型均為扭轉模態。定量分析，其滾轉、俯仰、偏航三方向均存在10 Hz左右的頻率，一階、二階、三階振型分別為:9.89 Hz，10.26 Hz，12.77 Hz。

系統單點吊掛釋放，由于電磁鐵消磁過程受力的不均勻性，主平臺引進三軸干擾角速度的同時會引起平臺自身的振動。

4.2 地面模擬試驗結果分析

觀察地面模擬試驗的分離角速度曲線，小衛星模擬件在上支撐出筒前與主平臺在滾轉與偏航方向存在10 Hz左右的振蕩頻率，如圖7(AC段曲線)所示。說明該振蕩為試驗系統自身引起，而非偏心分離過程機構運動導致，不影響利用地面試驗探尋筒式偏心分離小衛星的分離姿態規律。

盡管地面模擬試驗存在系統自振、風阻等干擾因素影響，但仍可從定性角度比較仿真與地面試驗結果，從小衛星的分離角速度曲線可明顯看到上支撐出筒點和下支撐出筒點曲線變化規律與物理模型仿真結果曲線基本一致。

地面試驗結果表明，對該類筒式偏心分離小衛星的分離動力學研究采用平動副約束的簡化模型與真實模型存在本質區別，是不可取的。

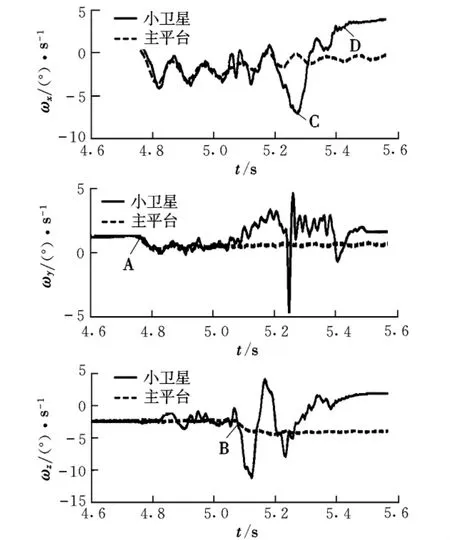
圖7 小衛星與主平臺角速度曲線

4.3 分離過程力學現象與機理

結合物理模型的仿真結果與地面模擬試驗結果，對筒式偏心分離小衛星的分離過程力學現象與機理進行分析和總結。分離過程中的力學現象如下:在上支撐出筒前，小衛星跟隨主平臺一起運動;上支撐出筒以后，小衛星三軸角速度反向增加，主平臺的三軸角速度基本維持不變，如圖8所示。

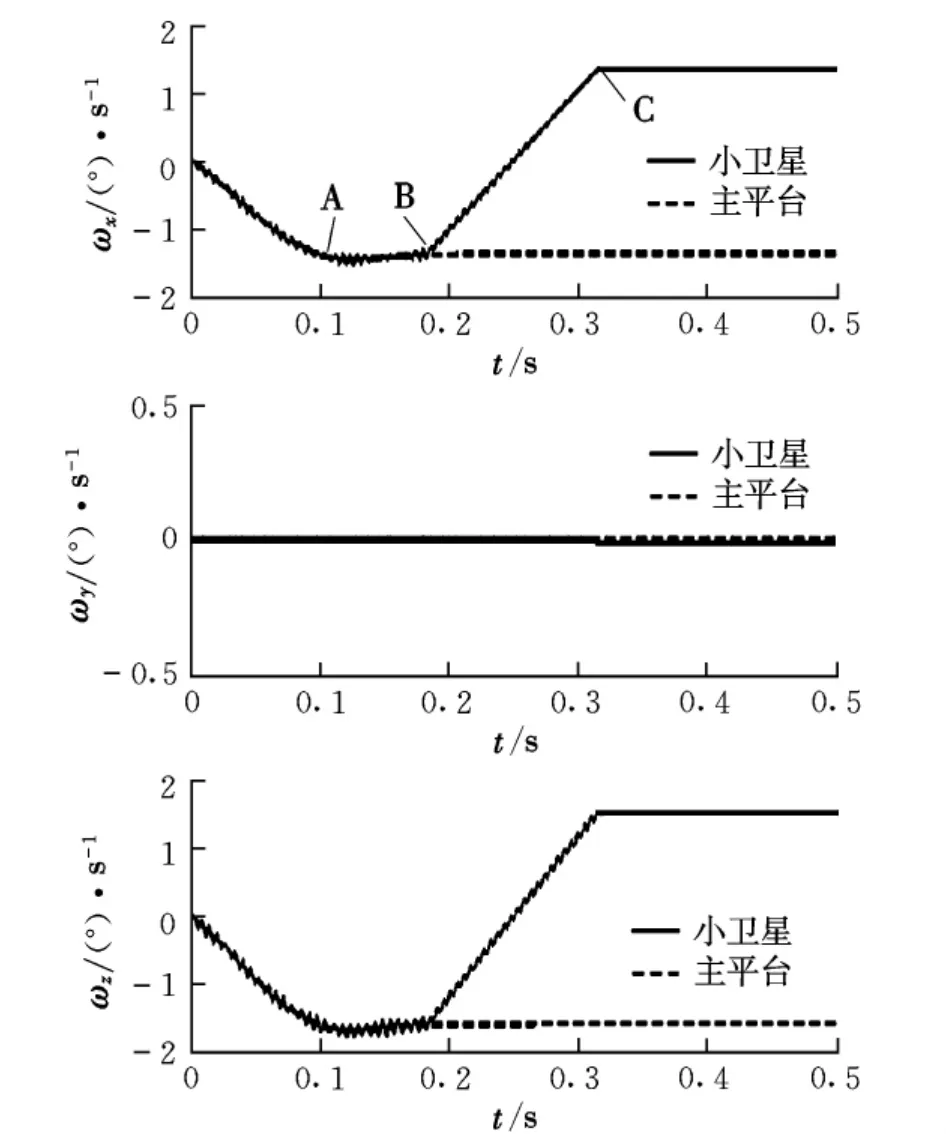
圖8 小衛星與主平臺分離角速度曲線

分離過程機理:偏心分離過程可看成類似平動與轉動牽連運動的組合運動過程。整個分離過程可簡單劃分為三個工作時段:分離彈簧作用行程、上支撐作用行程和下支撐作用行程。小衛星質心介于上下支撐間，當小衛星的上下支撐與釋放筒上的導軌同時作用，可近似等效為小衛星與釋放筒間為平動副作用，小衛星與主平臺有相同的角速度;上支撐出筒后，單獨在下支撐作用下，根據轉動牽連運動原理將使小衛星產生一個與主平臺方向相反的角加速度(科氏加速度)，小衛星的角速度反向增長。

5 結束語

本文從理論角度研究分析了筒式偏心分離小衛星的動力學過程，平動副約束簡化模型與物理模型的仿真結果存在較大差別，利用地面模擬試驗從定性角度較好地驗證了物理模型的仿真曲線規律，說明采用平動副約束模型來簡化該類筒式偏心分離過程的方法是不可取的。最后總結了該類偏心分離小衛星過程的力學現象與機理，為最終解決該類工程問題打下理論基礎。

［1］ 王功波.小衛星在軌釋放有關問題研究［D］.長沙:國防科學技術大學，2006:1-6.

［2］ 張華，肖余之，徐博侯，等.空間飛行器的對接分離與地面模擬試驗的仿真分析研究［J］.宇航學報，2008，29(6):1761-1765.

［3］ 蔣超，王兆魁，范麗，等.衛星筒式偏心在軌分離動力學分析［J］.飛行力學，2010，28(1):76-79.

［4］ Lee TW，Wang A C.On the dynamics of intermittent-motion mechanisms，Part1:dynamics model and response［J］.ASME Journal of Mechanisms，Transmissions and Automation in Design，1983，10(5):534-540.

［5］ 章為仁.衛星軌道姿態動力學與控制［M］.北京:北京航空航天大學出版社，1998.

［6］ 洪嘉振.計算多體系統動力學［M］.北京:高等教育出版社，2002.