動態環境下在線航跡規劃的滾動優化方法

魏鐵濤，王劍薇，屈香菊

(北京航空航天大學航空科學與工程學院，北京 100191)

引言

基于分層規劃的思想，飛行器的航跡規劃一般可分為離線航跡規劃和在線航跡規劃兩個階段［1］。其中，離線航跡規劃通常在起飛前進行，根據當時已知的環境和任務信息，生成折線形式的參考航跡，飛行器沿此參考航跡在安全走廊內飛行［2］。但由于離線航跡規劃通常沒有考慮飛行器的機動性約束，所以得到的航跡不可直接使用，還需要進一步進行更細致的規劃，即分層規劃的第二層——在線航跡規劃。

在線航跡規劃的任務，是在飛行過程中利用較細致的實時環境與任務信息，在以參考航跡為中線的安全走廊內規劃出一條安全可飛的可行航跡。可行航跡在飛行器的控制中起到導引的作用，飛控系統以此為指令信息引導飛行器按預定航跡飛行，通常也被稱為指令航跡。指令航跡應該盡量貼近參考航跡，使得兩者間的偏差盡可能小，并滿足飛行器的機動性能約束。因此，在線航跡規劃屬于帶約束的最優控制問題。當飛行器在動態環境下執行任務時，環境信息的改變有可能導致預先規劃得到的參考航跡不可用，需要重新規劃出新的參考航跡才能滿足環境約束。在這種情況下，在線航跡規劃需要兼顧快速性與精確性，在較短的時間內為飛行器生成新的指令航跡，引導飛行器安全飛行。

大多數軍用和民用的在線航跡規劃問題都是采用固定時域的優化方法，單純以指令航跡與參考航跡之間的航跡偏差最小為優化目標。由于飛行器的在線航跡規劃是在不斷運動中規劃前方航跡段的，采用固定時域的搜索尋優方法，指令航跡的實時性將會比較差［3-5］。參考航跡的突然變化，容易引起指令航跡與參考航跡之間的航跡偏差急劇增大，甚至飛出安全走廊，導致任務失敗。文獻［6］提出了一種偏差微分綜合控制方法，在性能指標中引入偏差微分項，能夠抑制解的振蕩，得到合理有效的控制律，該方法在靜態和已知環境中的應用具有較好的性能，但對于動態或未知的環境卻有很大的局限性。模型預測控制(Model Predictive Control，MPC)算法對于處理動態環境中的航跡規劃問題具有一定的優勢，滾動時域的在線優化能更好地適應系統參數以及環境的動態變化［7］。然而，傳統MPC的計算量較大，限制了它在很多動態系統中的應用。過去十年中，許多學者提出了許多改進的方法來解決MPC算法的精度和速度之間的矛盾。James和 Vesna［8］簡化了有限域MPC優化算法，使用末端懲罰來提高算法的解算速度。David等［9］基于MPC算法，引入一個勢函數(Potential Function)，該函數將可能運動障礙物或其它飛行器的狀態信息反映到代價函數中，計算量較小，可用于直升機的在線航跡規劃。文獻［10］用Gradient-Descent方法解決最小化問題，可以將計算量減少到一定程度以用于RUAV的實時航跡規劃。文獻［11］應用擾動分析理論將系統的非線性模型在標準軌跡(Nominal Trajectory)的基礎上線性化，將有限時域最優控制問題變為一個易處理的凸優化問題。

以上幾種改進的MPC方法在一定程度上降低了計算量，可應用于低速飛行器的在線航跡規劃問題。但是，在飛行速度較大，或參考航跡的航向改變較大的情況下，上述方法的精度可能變低。針對此問題，本文提出一種動態環境下在線航跡規劃的滾動優化方法，通過引入一個新的終端懲罰項，使得指令航跡的性能指標能夠更好地反映飛行器在未來飛行段指令航跡與參考航跡發生偏差的趨勢。有助于飛行器對前方變化后的航跡方向提前作出反應，以提高動態環境下的在線航跡規劃性能。

1 飛行器模型

在平面笛卡爾坐標系內建立飛行器的運動學模型。飛行器的運動用其位置(ξ，η)、速度(V)和偏航角(χ)描述。飛行器的運動學離散模型為:

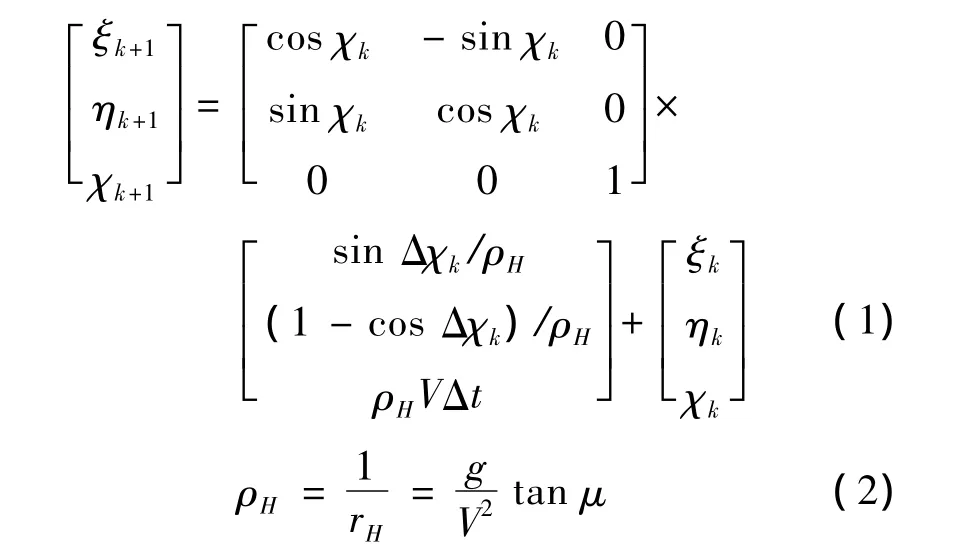
式中，χk為偏航角;(ξk，ηk)為飛行器在采樣時刻 k的位置;ρH為水平航跡的曲率半徑。飛行器協調轉彎飛行，χk+1是經歷時間間隔Δt后的偏航角，相對于k時刻的增量為Δχk。圖1顯示了上述變量的幾何關系。

圖1 變量幾何關系圖

飛行器在采樣時刻k+1的狀態，包括χk+1，ξk+1和ηk+1，可以通過下述公式計算:

2 滾動優化方法

2.1 模型預測控制

模型預測控制是一種滾動的、有限時域內的優化控制算法，使用被控對象的預測模型來預測其未來的響應和狀態。在滿足輸入和狀態限制約束下，在有限時域內對控制量進行滾動優化［4］。

模型預測控制在每一個采樣時刻，將系統的當前狀態作為初始條件，計算在有限控制時域內系統的未來響應，再根據該優化對象的性能指標，求解一個開環最優化問題，得到一個控制量的輸入序列，并將該控制序列的第一項作用于被控對象。在下一采樣時刻，用新的飛行器狀態，重復求解上述優化問題，從而形成閉環控制。圖2直觀地顯示了模型預測控制的基本思想。

圖2 模型預測控制基本思想

2.2 性能指標的建立

首先，為了使飛行器的指令航跡盡可能貼近參考航跡，應該尋求最優控制使指令航跡與參考航跡之間的偏差最小。所以，在建立性能指標函數時，首先考慮到在性能指標中對控制域內的航跡偏差進行加權，即按航跡偏差最小確定性能指標。該指標為:

在按航跡偏差最小確定性能指標時，控制變量往往會出現劇烈振蕩。為了抑制解的振蕩，可以在性能指標中增加一個偏差微分項，對變化過程進行控制［5］。增加微分項后的性能指標可表示為:

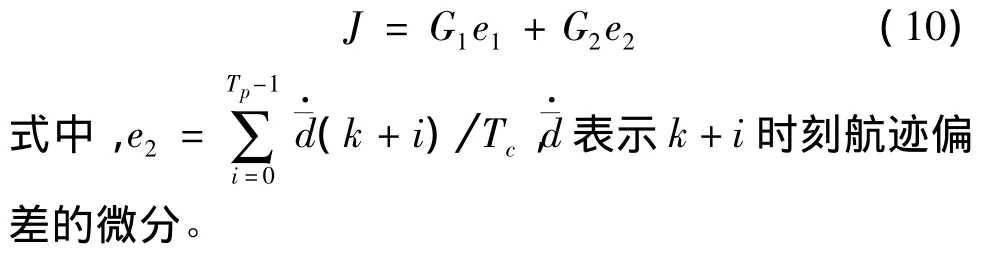
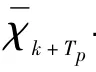
2.3 算法流程

基于模型預測控制的動態環境下在線航跡規劃方法包含以下步驟:

(1)更新預測時域內的環境信息和參考航跡。(2)在每個采樣點k，計算未來有限控制時域內可能的飛行器狀態。

(5)從時刻k+1開始，重復上述步驟，直到任務完成。

3 影響因素分析

3.1 滾動優化的影響

假定某型飛行器執行動態環境下的飛行任務，參考航跡會根據前方環境的變化而實時更新，最終執行的參考航跡如圖3所示。要求在線航跡規劃能夠及時精確地跟蹤調整后的參考航跡，生成合理的指令航跡。

分別采用傳統的固定域內的在線航跡規劃方法和本文提出的動態環境下的在線航跡規劃方法，對此航跡規劃問題進行仿真計算。飛行器采用式(1)的運動學模型，可得指令航跡與參考航跡之間的航跡偏差(e)隨時間變化情況如圖4所示。仿真結果表明，采用模型預測控制進行在線航跡規劃時，指令航跡與參考航跡的偏離程度要比傳統的固定時域的控制方法明顯改善。

圖3 參考航跡

圖4 指令航跡偏離誤差對比

3.2 控制域長度的影響

控制時域長度Tc的選擇對指令航跡偏離程度和計算時間有很大影響。經過多次試算，取預測時域長度Tp=6 s，對3.1節提出的航跡規劃任務進行仿真。圖5和圖6分別給出了在速度為150 m/s，125 m/s，100 m/s，85 m/s 時，采用不同控制域長度情況下的指令航跡偏差和計算時間t。在預測時域給定的前提下，控制時域選得越小，意味著對未來飛行器狀態的控制能力越弱，反映在性能指標中效果也就越差。同時較大的控制時域長度將使計算量增加，影響在線航跡規劃的實時性。故控制時域長度的選取要在算法的快速性和精確性之間綜合權衡，根據具體的飛行任務來確定。

在本例中，綜合考慮航跡偏差程度和計算時間的大小，控制時域長度選為4 s時綜合性能最好。

圖5 不同控制域的航跡偏離誤差

圖6 不同控制域的計算時間

3.3 預測偏航角偏差權重的影響

綜合考慮間隔時間ΔT和性能指標對優化結果的影響，取ΔT=1 s，根據多次的試算，取各項權重G1=0.6，G2=0.3，G3=0.1，對 3.1 節提出的在線航跡規劃任務進行仿真。當在預測時域內發生前方參考航跡的方向變化時，才給G4賦值，G4分別取為0.1，0.3，0.6 和 0.9。

圖7表示在不同權重G4條件下，指令航跡與參考航跡之間的航跡偏差;圖8為不同G4條件下，在參考航跡轉折點附近的指令航跡細節圖。可以看出，G4越大，在預測時域內發生參考航跡的轉折時，飛行器對前方參考航跡的方向改變能夠更早作出相應反應，使得指令航跡與參考航跡的偏差更小。

圖7 航跡偏差情況

圖8 參考航跡航向變化點附近指令航跡細節圖

4 仿真示例

假設飛行器進入一個如圖9所示的存在若干需要規避的障礙物(用陰影表示)的未知區域，由于探測能力的限制，飛行器只有在接近障礙物時才能發現并對其當前參考航跡作出調整。要求為飛行器在線規劃一條滿足機動性能約束的指令航跡，并保證其與不斷更新的參考航跡之間的偏差盡可能小，各參數的取值如表1所示。

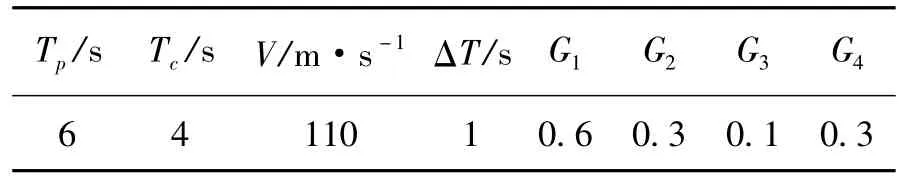
表1 各參數取值

采用本文提出的在線航跡規劃滾動優化方法和傳統的固定時域規劃方法分別進行仿真計算，規劃結果如圖9所示。其中傳統固定時域的規劃方法耗時245.6 s，平均航跡偏差42.8 m;而滾動優化方法耗時175.5 s，平均航跡偏差13.9 m。

圖9 在線航跡規劃結果

在動態環境下，由于飛行器是在不斷運動中規劃前方可行航跡的，這時如果采用傳統的規劃方法，在線規劃的實時性將比較差，參考航跡的突然變化，容易引起飛行器指令航跡的航跡偏差急劇增大，甚至偏離出安全走廊的范圍導致任務失敗，如圖9中的A點所示。而采用在線航跡規劃的滾動優化方法，在參考航跡方向發生突然改變時，能夠迅速作出相應反應，航跡偏離程度有了很大改善，規劃速度與固定時域的規劃方法相比也有所提高。

5 結束語

本文以平面內的固定翼飛行器為例進行研究，但提出的動態環境下在線航跡規劃的滾動優化方法可以擴展應用于更廣泛的領域，包括三維空間內、水下、空間及地面交通工具的航跡規劃等。但是，三維空間內的航跡規劃問題對規劃速度的要求將會更高，并且滾動優化方法的影響因素也呈現出一些特點，這些需要進一步的研究。

［1］ Shim D H，Kim H J，Sastry Shankar.Hierarchical control system synthesis for rotorcraft-based unmanned aerial vehicles［C］//AIAA Guidance，Navigation and Control Conference.Denver，CO，2000.

［2］ 魏鐵濤，屈香菊.多機協同與多目標分配任務規劃方法［J］.北京航空航天大學學報，2009，35(8):917-920.

［3］ Ross IM，Fahroo F.Pseudo spectral knotting method for solving non-smooth optimal control problems［J］.Journal of Guidance，Control，and Dynamics，2004，27(3):397-405.

［4］ Schouwenaars Tom，How Jonathan，Feron Eric.Receding horizon path planning with implicit safety guarantees［C］//Proceeding of the 2004 American Control Conference.Boston，2004.

［5］ 王忠俊.非線性飛行控制方法研究概述［J］.飛行力學，1995，13(3):24-28.

［6］ 何佩，屈香菊，武哲.航跡跟蹤的優化方法研究［J］.北京航空航天大學學報，2003，29(7):599-601.

［7］ Wang Liu-ping.Model predictive control system design and implementation using MATLAB ［M］.London:Springer，2008.

［8］ Primbs JA，Nevistic V.A new approach to stability analysis for constrained finite receding horizon control without end constraints［J］.IEEE Transactions on Automatic Control，2000，45(8):1507-1512.

［9］ Shim D H，Kim H J，Sastry Shankar.Decentralized nonlinear model predictive control of multiple flying robots［C］//IEEE Conference on Decision and Control.Hawaii，2003.

［10］ Kim H J，Shim D H，Sastry Shankar.Nonlinearmodel predictive tracking control for rotorcraft-based unmanned aerial vehicles［C］//American Control Conference.Anchorage，AK，2003.

［11］ Singh Leena，Fuller James.Trajectory generation for a UAV in urban terrain，using nonlinear MPC ［C］//Proceedings of the IEEE American Control Conference.Arlington，VA，2001:2301-2308.