極大似然法在飛機起飛性能參數辨識中的應用

于雪梅，程偉，谷偉巖

(1.北京航空航天大學航空科學與工程學院，北京 100191;2.中航通用飛機有限責任公司試飛交付中心，廣東珠海 519015)

引言

飛行器氣動參數辨識自 Warner和 Norton［1］的早期工作以來，已經有九十多年的歷史。以往飛行器氣動參數的確定是通過理論計算和風洞試驗進行的，而理論計算有其局限性，風洞試驗與實際飛行條件也存在差異，兩者所得到的氣動特性均難以準確反應實際飛行特性。因此，飛行試驗是確定飛機飛行性能最有效的方法，應盡可能在飛行試驗的基礎上確定飛機在使用范圍內的飛行性能，但這樣不可避免地存在耗資大、周期長的問題。

隨著計算機和數值計算技術的發展，系統辨識理論在飛行器設計和研制過程中的作用越來越大，尤其是經過20世紀60年代后期以來的研究，飛機氣動參數辨識已發展成為一個較為獨立的系統辨識分支［2］。極大似然法是參數辨識領域中常用的一種方法，理論上已經證明參數的極大似然估計是一致漸進、有效、無偏的估計，且具有良好的收斂性［3-4］，因而該方法在飛行器參數估計中得到廣泛應用。目前，世界發達國家對飛機狀態估計和參數辨識的研究已發展到實用水平［5-6］。我國學者在飛行器的飛行試驗參數識別方面也進行了許多研究，但總體來說，大部分研究都集中于操縱特性的氣動導數和模態特性研究上［7-8］，對于飛行性能的氣動參數識別和總體特性研究并不多見。

本文結合Y12飛機雙發起飛飛行試驗實測數據，研究了利用極大似然法進行飛機起飛性能參數辨識的問題，建立了Y12飛機起飛性能的數學模型，并從簡化靈敏度導數計算角度提出了以飛機在起飛滑跑過程中速度增量為觀測量的觀測方程［9］，分析給出待辨識參數和利用極大似然法進行起飛參數辨識的方法，采用Matlab軟件進行了系統仿真［10］，并針對主要辨識影響因素變化對結果的影響進行了討論。

極大似然法與以前關于飛機起飛性能的數據處理方法相比具有較高的處理效率和辨識精度，因此，將極大似然法應用于飛機起飛性能參數辨識具有一定的現實意義，既可提高工作效率，又可節約試驗成本。

1 飛機起飛性能建模

起飛性能涉及的內容包括:全部發動機工作正常起飛、一臺發動機失效繼續起飛、一臺發動機失效中斷起飛。本文僅研究利用極大似然法對全發起飛地面滑跑起飛性能的辨識。

1.1 起飛性能數學模型

從動力學角度分析，在不考慮跑道坡度的情況下，飛機在滑跑過程中承受的力有:飛機重力(G)、發動機推力(P)、氣動阻力(D)、地面摩擦力(Ff)、地面對機輪的支持力(N)、機翼升力L。飛機起飛滑跑段的運動方程可簡化為［10］:

式中，CL，CD分別為飛機起飛構型狀態下(襟翼在起飛位置、起落架放下等)對應于停機迎角的升力系數、阻力系數;f為地面滑跑摩擦系數;ρ為大氣密度;SW為機翼面積。一般情況下，發動機推力P是飛行速度、高度的函數，由發動機廠家提供。

飛機在滑跑過程中各力隨飛行速度的變化如圖1所示。圖中，Q為總阻力;VLOF為離地真速。在起飛離地點處有:V=VLOF，L=G。

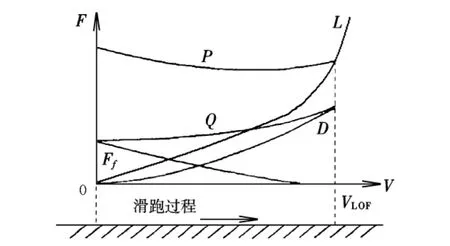
圖1 起飛滑跑過程中各力隨速度的變化曲線

式(1)和式(2)中的速度均為飛行真速(VT)。因為飛機升力、阻力的大小只與真速有關，而起飛滑跑距離的大小卻與地速(VG)有關，因此需考慮風對起飛距離的影響。真速和地速的關系為VG=VT±VW(逆風取“－”，順風取“+”)。起飛滑跑距離可表達為d S=VGd t，積分則可獲得起飛地面滑跑距離為:

將各參數的表達式帶入式(1)，并除以G，有:

式中，CL，LOF為離地瞬間的升力系數。

由式(3)可見，影響起飛滑跑距離的主要因素有:起飛質量、襟翼狀態、跑道條件(粗糙度、場壓)、外界大氣環境(場溫、風速風向)等。起飛滑跑距離表達式中有3個未知參數(CD，CL，f)，如取綜合阻力系數 A=(CD－fCL)，則待辨參數變為 f，A。

1.2 起飛性能辨識模型及辨識方法

根據極大似然法的辨識原理，在進行參數辨識前，首先需要選擇觀測量并給出觀測方程［3］。如將式(3)作為觀測方程，將L視為觀測量，則待辨識參數f和A值位于分母中，計算中發現，此時靈敏度導數不易計算。因此，分析后選擇起飛滑跑過程的速度增量為觀測量，以簡化觀測方程，便于進行靈敏度導數計算和參數辨識。

將起飛滑跑過程分為足夠多的小段，每一小段均可視為勻加速過程，則由式(3)可得速度增量為:

由式(8)可見，代價函數相當于測量量和觀測量的累計差值，根據模型要求，其值可以適當變化。一般計算時，當|Jj+1－Jj|/|Jj|＜ε(迭代精度)時停止迭代，亦可事先定義代價函數或迭代次數進行迭代并檢查收斂情況。

2 起飛性能飛行試驗及數據采集

起飛性能飛行試驗測試的目的就是通過準確測量飛機在起飛過程中的滑跑距離、速度、姿態、發動機功率等參數的變化規律來確定起飛性能。Y12飛機起飛性能的測試參數包括:飛機起飛質量、起飛襟翼偏度、大氣溫度、機場場壓高度、風速、風向、指示空速、水平滑跑距離、發動機功率(包括螺旋槳轉速和扭矩)、起飛松剎車信號、前輪離地信號等。以Y12飛機雙發起飛性能為例，某一狀態(起飛質量5 300 kg，起飛襟翼0°，大氣溫度 －14℃，機場高度145 m，逆風風速0.5 m/s)的指示空速、高度、發動機扭矩測試結果如圖2所示(由于篇幅限制，其它參數未繪出)。

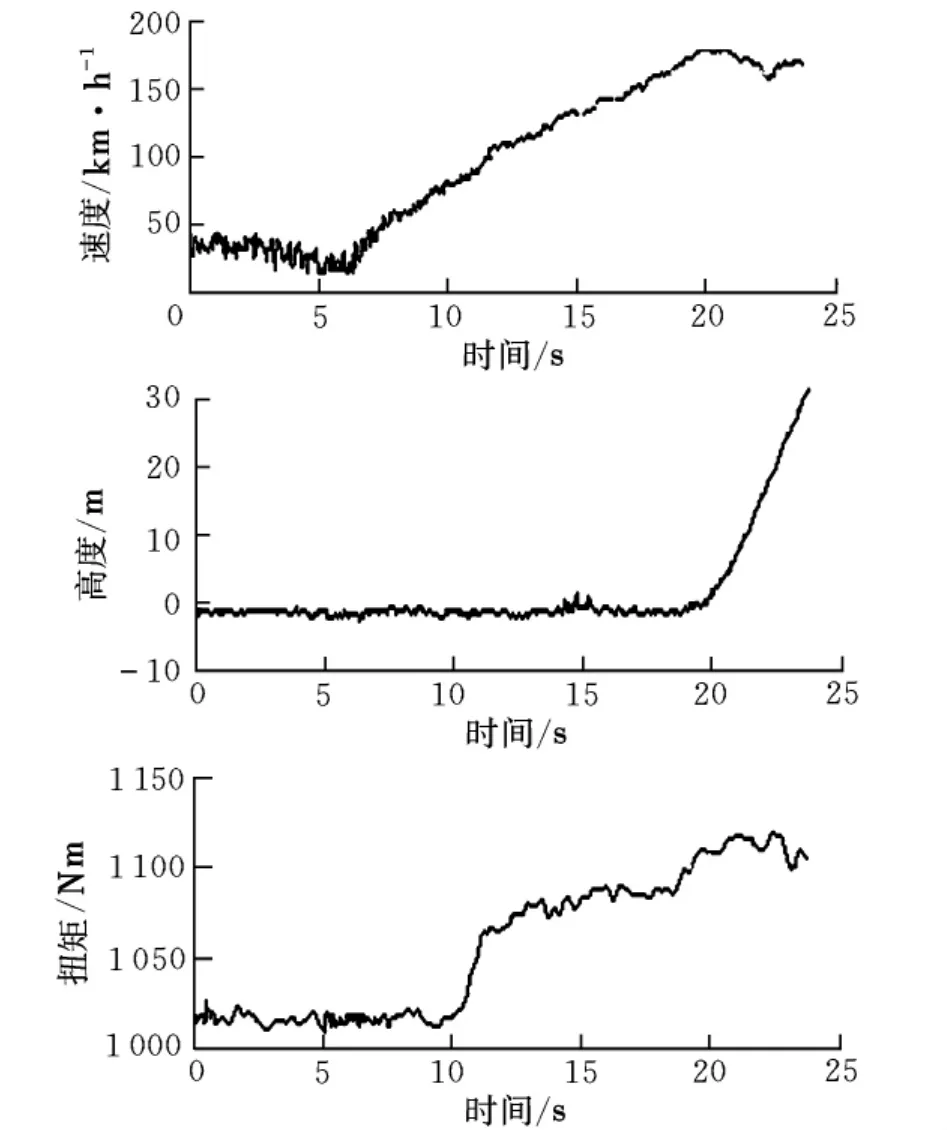
圖2 飛機起飛測試結果

以上僅給出一組測試數據，實際辨識過程中采用取多組測試數據進行，將辨識結果取平均值作為這一狀態飛行的待辨參數值。

3 極大似然法參數辨識

采用Matlab軟件進行編程，具體辨識步驟如下:

(1)對機載測試數據(圖2)進行預處理(主要包括濾波、中值、曲線擬合)，并將校正空速轉換成真速，選取合適辨識數據段，建立測試結果數據文件。

(2)根據試驗狀態、飛機參數和發動機參數，計算對應試驗狀態的發動機推力和大氣密度。

(3)根據待辨識參數的理論計算結果和工作經驗，選取待辨識參數的迭代初值。對于Y12飛機，在起飛地面滑跑過程中，有關參數的取值范圍為:

地面滑跑摩擦系數:f=0.03～0.04

機翼面積:SW=34.27 m2

阻力系數:CD=0.16～0.20

升力系數:CL=1.2～1.4

計算得綜合阻力系數:A=4.1～5.2

因此，在迭代初始，兩個待辨識參數f和A的初值應在上述范圍內取值。

(4)將飛行速度隨時間的變化轉換為速度增量隨時間的變化并作為觀測量，建立數據文件。

(5)選擇樣本長度N=100。

(6)合理選擇代價函數和迭代精度或迭代次數，按極大似然法計算待辨參數的靈敏度導數和代價函數，進行迭代計算。最終使辨識參數經過有限次數的迭代后，收斂于一個合理、可信的結果。在本文的參數辨識過程中，經過比較，選用了人工控制迭代次數的方法。

經上述步驟，得到辨識結果如表1所示。

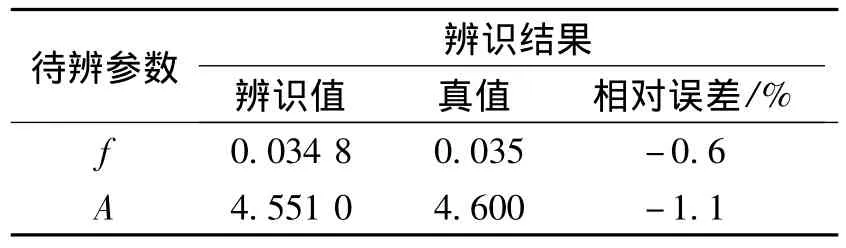
表1 起飛參數辨識結果

真值是Y12飛機經過多年飛行試驗確定的結果，比較真實可信。從表中可見:辨識結果與真值的相對誤差約為1%。將試驗時飛機的狀態參數、飛行參數和辨識值/真值分別代入式(3)中進行計算，可得到起飛滑跑距離的擴展結果分別為407 m，419 m，從工程應用角度看，該辨識結果能夠滿足性能試飛精度要求。

辨識參數迭代結果如圖3所示。

圖3 辨識參數迭代結果曲線(J=0.01)

由圖3可見，經過30次的迭代后，辨識參數已基本趨于穩定。迭代過程的變化趨勢說明了迭代的收斂性。由于迭代曲線縱坐標的取值范圍很小，因此，曲線在迭代到30次后雖然看似有一定的波動，但其實際變化范圍已經很小，可以認為曲線收斂。

4 辨識結果影響因素分析

4.1 迭代初值影響

將地面滑跑摩擦系數f和綜合阻力系數A的迭代初值分別有意識地放大和縮小，采用同樣的數據處理和辨識方法進行辨識。結果表明，經過40次左右的迭代后，迭代參數的波動范圍已趨正常范圍，因此，本文采用的方法對迭代初值偏差具有良好的適應性。

4.2 代價函數影響

分別采用J=0.05，J=0.01和J=0.005三種代價函數進行對比計算，結果表明:代價函數越小，迭代次數越多，但迭代結果并沒有顯著提高，f基本在0.034 6～0.035 0之間波動，波動幅度為1%，A基本在4.550 5～4.551 3之間波動，波動幅度小于0.1%。因此，選擇合適的代價函數可以經過較少次數的迭代就可以獲得滿意的結果。

4.3 迭代次數影響

分別采用50，100和500三種迭代次數進行計算，結果表明:迭代次數增多對迭代結果沒有顯著影響。因此，在進行參數辨識時，應選擇合適的迭代次數，可以通過較少次數的迭代獲得滿意的結果。

4.4 敏感參數影響

在進行測試數據參數辨識初期，對測試數據進行預處理后，參數辨識結果很不理想，辨識結果在一個較大的范圍內波動，有時還出現發散現象。

經過對觀測方程式(5)的分析發現，對Y12飛機的狀態參數和試驗數據而言，方程式(5)中的ΔV和C0兩項為同一量級，C1θ1項比ΔV低一個量級，而C2θ2U項則低至少兩個量級。在開始進行實測數據參數辨識時，觀測量ΔV的有效位數取值到10－1，這樣，其它參數的變化就被ΔV的取值誤差吃掉了。因此，觀測量ΔV和C0的精度對辨識結果具有重要影響。結果表明，將觀測量ΔV和C0的有效位數取到10－3，參數辨識結果明顯改善。

因此，觀測方程中各個參數對辨識結果的影響作用是不一樣的。在參數辨識前，應初步對觀測方程中的各個參數進行敏感性分析，以保證測試數據的選取有足夠的精度。

4.5 試驗數據段的選取

對Y12飛機起飛性能測試而言，由于速度傳感器有效工作范圍的限制(小速度指示誤差較大)，起飛滑跑段速度的有效范圍基本在50 km/h以上，從該速度到飛機起飛離地，對應的時間歷程約為10 s左右。測試系統的采樣率較高(通常50～100 Hz)，雖然理論上選取任意幾秒作為數據段測試數據點都足以進行參數辨識，但實際上數據段的選取對辨識結果有一定影響，應當有目的地選取測試數據段。

從觀測方程式(5)可見，式中C2θ2U項比觀測量ΔV低一個量級甚至更多，而U為起飛滑跑速度的平方，因此，為使C2θ2U項與觀測量ΔV項具有更接近的量級，試驗數據段應盡量在較大速度范圍內選取。

4.6 樣本長度影響分析

極大似然法在理論上希望樣本長度越大越好，然而實際樣本過長不僅會增加計算量，而且數據中非理想誤差的增加也會影響參數辨識結果。為確定樣本長度對辨識結果的影響，本文進行了不同樣本長度的對比辨識，在同樣的測試數據段內，分別進行樣本長度N=100和N=500情況的迭代，迭代結果表明:對Y12飛機起飛性能進行辨識，在同樣迭代次數的情況下，樣本長度的增加并沒有使迭代收斂增快，在樣本長度N=100的情況下，已具有比較滿意的辨識結果，當樣本長度N=500時，辨識結果精度并沒有顯著提高，而迭代計算需要的時間卻顯著增加。

5 結束語

本文研究了利用極大似然法進行飛機起飛性能飛行試驗數據參數辨識的問題，確立了辨識模型和待辨參數，采用Matlab軟件進行計算，結果表明極大似然法可以快速、準確地辨識出起飛性能所需的參數，并具有較高的精度。從工程實用的角度出發，辨識中所使用的觀測方程應具有簡單的形式，以便于靈敏度導數的計算。在觀測方程中，各參數對辨識結果的影響是不一樣的，為保證辨識結果的準確性，應進行敏感參數分析，確保測試數據的記錄具有足夠的精度。另外，代價函數、迭代次數、樣本長度、數據段的選取等對參數辨識結果精度都可能有影響，在參數辨識過程中應注意分析，以盡可能經過較少迭代獲得最優結果。與傳統方法相比，極大似然法具有數據處理效率高、辨識結果精度高的特點，在今后的飛機起飛性能數據分析中應進一步推廣，并應探索將其應用到其它性能分析中的方法。

［1］ Warner E P，Norton F H.Preliminary report on free flight test［R］.NASA Report No 70，1919.

［2］ 蔡金獅.飛行器系統辨識學［M］.北京:國防工業出版社，2002:287-294.

［3］ 葉建華.過程辨識技術［M］.上海:上海大學出版社，2007:59-82.

［4］ 王志賢.最優狀態估計與系統辨識［M］.西安:西北工業大學出版社，2004:223-243.

［5］ Klein V，Mogan DR.Estimation ofbias errors inmeasured airplane responses using maximum likelihood method［R］.NASA TM-89059，1987:79-82.

［6］ Maine R E.Programmer’smanual for MMLE3，a general FORTRAN program formaximum likelihood parameter estimation［R］.NASA TP-1690，1981.

［7］ 全昌業.氣動參數辨識飛機飛行試驗研究回顧［J］.飛行試驗，1999，15(2):8-14.

［8］ 劉興堂，萬少松.一種估計飛行器運動特性的實用極大似然法［J］.飛行力學，1999，17(3):65-70.

［9］ 谷偉巖.運十二飛機起飛性能參數辨識研究［D］.北京:北京航空航天大學，2000.

［10］ 張靜.Matlab在控制系統中的應用［M］.北京:電子工業出版社，2008:364-83.