不同網格劃分方式的圓柱型舵桿繞流數值模擬結果比較
周上然
(海軍上海地區裝備修理監修室,上海 200000)
船舶在航行時,流體經過舵桿會產生渦。雷諾數在一定范圍時,流體在舵桿表面的后駐點附近脫落,脫落漩渦以周期性的交替方式離開圓柱表面,形成渦泄。渦泄的存在使得舵桿表面周期性變化的升力和阻力增加,從而導致物體的振動,影響了舵桿的穩定性。本文將舵桿簡化為二維圓柱模型,運用兩種網格劃分方式模擬Re=200時二維靜止圓柱的繞流情況,對模擬出的升力與阻力系數進行比較與分析。
1 數值建模
1.1 基本方程及邊界條件
對不可壓縮粘性流體,在直角坐標系下,其運動規律可用N-S方程來描述,連續性方程和動量方程分別為
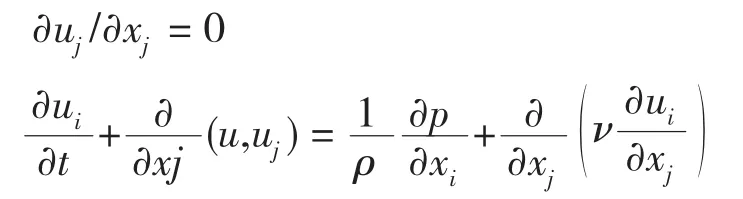
式中:
ui、uj分別為 x、y 方向的速度;
ρ為空氣密度;
p為壓力;
ν為流體動力粘度系數。
選取整個流場區域大小為30 D×55 D(D為立管直徑,D=0.02 m,ν=0.010 03 m/s),其中,上游為15 D,下游為40 D,立管圓心距上下兩側各15 D,左側、上側與下側設為速度入口,流體自左向右流動,右側為速度出口,圓柱壁面滿足無滑移固壁條件。本算例中雷諾數為200為層流流動,因此,在粘性模型的選取上采用Laminar層流模型。在計算方法上采用SIMPLEC方法,由于流動為非定常流動,為模擬瞬態流動,時間離散方式采用二階隱式,對壓力項離散格式采用二階精度。
1.2 網格劃分
流場計算區域選為55 D×30 D,圓柱距入口邊界為15 D,上下邊界距圓柱為15 D,D為物體垂直于來流方向平面上的特征尺寸,對圓柱一般取直徑,D=0.02 m,ν=0.010 03 m/s。
網格高度對于計算結果是否精確有著決定性的作用,對于層流模型,圓柱近壁處第一層網格高度需要滿足y+≈1,根據如下公式估算第一層網格控制點離開壁面距離△y:

第一種方法對計算區域進行了劃分,中心圓柱采用O型網格并進行局部加密,右側采用漸變的結構網格以提高計算效率,如圖1所示。第二種方法將全流場分為9個區域,采用四邊形結構網格對中間圓柱周圍4D區域及尾流區進行局部加密,如圖2所示。
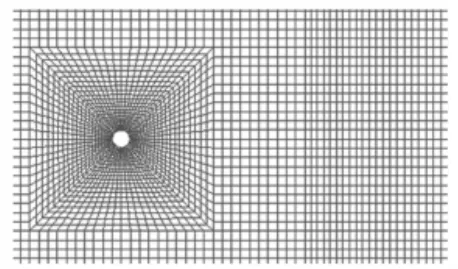
圖1 網格劃分

圖2 網格劃分
1.3 計算結果及分析
圖3、4分別為第一種與第二種網格劃分(Re=200)時的渦街脫落圖。

圖3 渦街脫落圖

圖4 渦街脫落圖
兩種網格模擬的現象清晰,基本相同,可以認定兩種方式均可以模擬光滑圓柱舵桿繞流。
2 模擬結果的比較與分析
2.1 升力系數與阻力系數的分析
圖3、圖4的現象清晰的模擬了光滑立管尾流場,因此,可認為兩種劃分方式均可行。圖5、圖6分別給出了兩種不同劃分格式的圓柱阻力系數與升力系數的時程曲線。從圖上可以看出圓柱尾流形成了卡門渦街,流動在150 s后趨于穩定,當位于圓柱上側的旋渦脫落后,圓柱上方壓力增加,此時圓柱下方旋渦還未脫落,壓力較小,上下兩側產生負的壓力差,反之當位于圓柱下側的旋渦脫落時,產生正的壓力差,因此,升力系數以y=0為平衡位置進行周期性震蕩,升力系數的均值為0。升力系數與阻力系數曲線在渦穩定脫落后,均呈現周期性變化[1]。兩種劃分方式計算出的結果:
(1)升力系數幅值為0.51,阻力系數在渦脫達到穩定后的均值為1.23。
(2)升力系數幅值為0.53,阻力系數在渦脫達到穩定后的均值為1.32。
從升力系數和阻力系數的周期性變化中,可以清楚的反映出圓柱上旋渦脫落的特性。均勻來流經過圓柱表面時,流動發生變化,產生邊界層分離后,在逆壓梯度的作用下,于圓柱上下兩個表面附近產生旋渦,旋渦在來流的作用下隨著流體向后運動,然后脫落。由于圓柱上下兩側的旋渦變化對流動方向上的壓差影響是一樣的,所以來流壓力差的變化,較垂直來流方向的壓力差變化快,變化速度是它的兩倍,這就很好的解釋了阻力系數的振蕩周期為升力系數振蕩周期的二分之一。
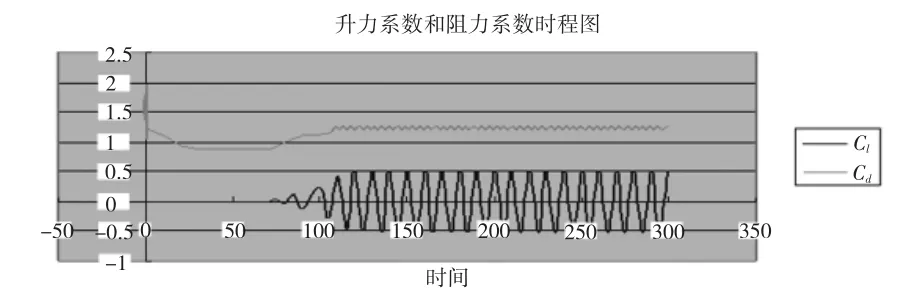
圖5 第一種劃分方式
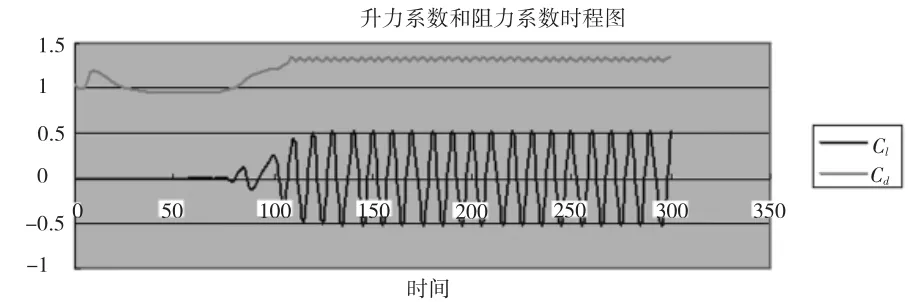
圖6 第二種劃分方式
對升力系數時程曲線做傅里葉變換,從時域轉換到頻域,第一種劃分方式計算出的主頻率為0.095 Hz,如圖7所示,第二種劃分方式計算出的主頻率為0.102 Hz,如圖8所示。
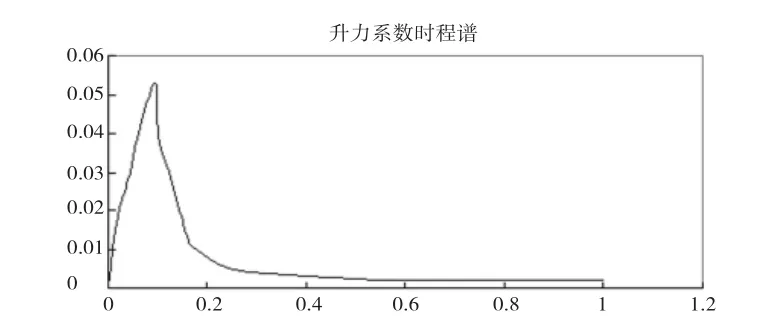
圖7 第一種劃分方式升力系數時程譜
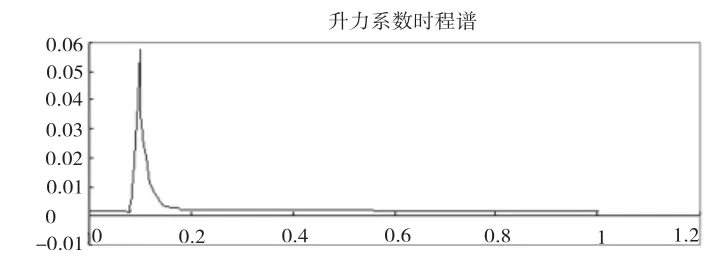
圖8 第二種劃分方式升力系數時程譜
2.2 斯特勞哈數(St)
St數是描述圓柱繞流的一個重要參數,其將邊界層分離及流動的不穩定性這些微觀的隨機特性,與表現相對穩定性的渦泄頻率聯系在一起[2],其定義為
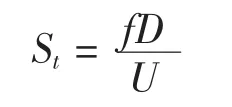
式中:
St為Strouhal數,表示旋渦的脫離情況;
f為圓柱渦泄頻率;
U為未受干擾的自由來流速度。
一般而言,在絕大多數的Re數區域內,St數相對穩定,這意味著渦泄有序。第一種劃分方式計算出Strouhal數為0.19,第二種劃分方式計算出Strouhal數為0.2。
2.3 結果比較
表1中給出了國內外的研究學者對雷諾數為200時的圓柱繞流數值計算[3]與實驗結果,通過比較,第二種劃分方式的計算出的Cl與Cd的值與實驗結果相接近,可以認為第二種劃分方式計算精度較高。
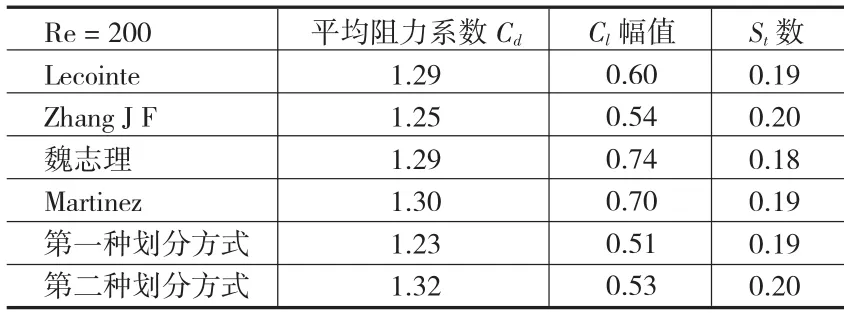
表1 Re=200時圓柱繞流數值計算結果與文獻數據比較
3 結束語
通過以上分析,我們得出以下結論:
(1)對Re=200的低雷諾數圓柱舵桿繞流,采用層流模型并結合合理的網格劃分,可以很好地模擬舵桿渦流運動,并通過對升力系數、阻力系數的分析,得到渦的脫落頻率。
(2)雖然兩種劃分方式都可以模擬出圓柱舵桿繞流運動,但是第二種方法計算出的升力系數、阻力系數更加接近實驗結果,因為,其在來流方向與垂直來流方向均加密了網格,較好的覆蓋了圓柱舵桿的分離區域。
(3)本文只對靜止的二維圓柱模型作了數值計算,未考慮圓柱的運動對流場產生的影響與三維模型的尺度效應。
[1]李 田,張繼業,等.二維彈性圓柱渦致振動尾渦模態[J].空氣動力學學報,2010,(06):25-26.
[2]顧 罡.二維圓柱繞流、雙圓柱繞流問題和三維垂蕩板運動的數值模擬[J].上海交通大學,2007,23-24.
[3]苑健康,黃維平.二維立管Helical Strakes繞流場的ANSYSCFD 分析[J].船海工程,2010,(04):26-27.

