被動聲納方位估計的寬帶盲源分離算法

范文濤，章新華，康春玉，蔣 飚

（1.海軍大連艦艇學院 博士生隊，大連 116018；2.海軍大連艦艇學院 信息與通信工程系，大連 116018）

方位估計，或稱波達方向估計（Direction of Arrival，DOA）是被動聲納表現目標態勢的方式之一［1］，其中又以方位估計精度和方位分辨率作為衡量DOA估計性能的重要指標。但是在淺海環境下，尤其是航道附近，往往存在各種強干擾源，嚴重影響了被動聲納對于弱目標的方位分辨性能和估計精度［1］，因此改善現有被動聲納方位估計性能顯得尤為迫切。

常規波束形成［2］是被動聲納中用于目標方位估計的常用方法，其優勢在于與環境無關，性能穩健。但是受到孔徑的限制，使得常規波束形成的方位分辨率始終無法突破瑞利限［2］。Capon［2］和 Schmidt［3］先后提出的基于陣列觀測數據協方差矩陣的高分辨方位估計算法，即 MVDR［2］和 MUSIC［3］算法，彌補了常規波束形成在方位估計方面的缺點。然而受到低信噪比、陣形失配或者源數目的限制，使得高分辨類算法在處理實際被動聲納數據時表現不夠穩健［4］。

近些年發展起來的盲信號處理［5］技術得到了研究者的廣泛關注，其中尤以對盲源分離技術［6-8］的研究居多。由于盲源分離算法所具有的特殊優點［6］，一些研究者將其引入到了水聲信號處理中［7］。文獻［6-9］成功地從多個輻射噪聲混合后的信號中分離出了所需源信號，驗證了盲源分離用于分離水下目標源的有效性，同時指出盲源分離算法可以分離空間上幾乎重疊的多目標源［9］。然而，這些方法同時存在對于海洋多途信道影響下的寬帶卷積混合源分離［7］研究較少的局限性。日本Sawatari課題組［10］針對室內多途混響下的源分離問題，提出了多種波束形成與盲源分離融合的處理結構，但是這些方法中的目標DOA估計均是為解決寬帶頻點間次序模糊而服務的。范文濤［11］、康春玉［12］針對被動聲納DOA估計與波形恢復，分別提出了將高分辨DOA估計算法與基于卷積混合的頻域盲源分離算法進行融合，改善了傳統高分辨算法的DOA估計性能。可是對于寬帶頻域盲源分離算法存在的頻點間次序模糊和頻點內尺度模糊問題［9］，依舊沒有較好的解決辦法。

基于時間結構的盲源分離算法［11］使用多個時間延遲二階相關矩陣來完成目標源的提取。但是這類算法同時存在時滯量選取難，對沒有時間結構特征的聲源的分離效果差等問題［11］。近期提出的非參數化獨立分量分析算法［13］可以對目標源的統計特性沒有任何先驗知識的前提下完成目標源的提取，是一種真正意義上的盲處理算法。考慮將兩者融合，既利用了目標源的時間結構特性，又可以在不需預知目標源統計特性的前提下完成源信號的分離，為了仿真比較方便，本文算法簡稱為時間結構非參數盲分離算法（Blind Temporal Structure Non-parametric Separation，BTSNPSEP）。本文根據寬帶卷積混合［14］，在每個子帶內將基于時間結構與非參數化特性的兩種盲源分離算法進行融合，建立新的解混矩陣代價函數，然后根據非線性最優化得到的解混矩陣得到子帶內方位能量譜，最后仿照寬帶頻域波束形成對所有子帶方位能量譜累加，得到總的寬帶方位譜。通過計算機仿真與實際海試數據，分別同經典MUSIC算法和MVDR方法進行了比較，結果表明本文方法能夠用于寬帶被動方位估計，尤其是強干擾背景下的弱目標檢測。

1 寬帶盲源分離算法

1.1 問題描述

考慮滿足半波長且陣元間距為d的均勻線列陣（Uniform Iinear Array，ULA），陣元數為N，各陣元之間無互耦。遠場寬帶目標源數目小于陣列陣元數目，即（Q＜N）。由此可以得到第i個陣元的卷積混合為［12］：

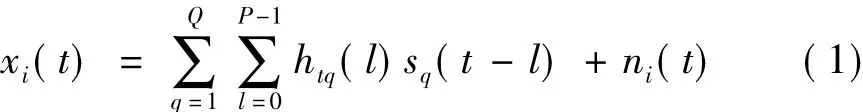
其中：htq（l）表示從目標源q到陣元i之間的沖激響應；P表示沖激響應的長度，ni（t）為疊加在每個陣元上的噪聲。

由于大部分盲源分離算法是基于瞬時混合模型的［7］，因此通過短時傅里葉變換 （Short-time Fourier transform，STFT）將時域卷積混合xi（t）變換為頻域信號xi（k，fj），可以表示為：

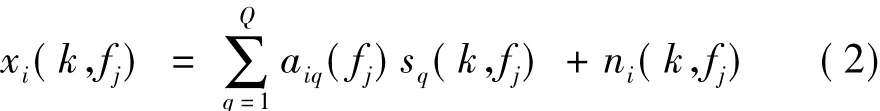
其中：fj表示第j個頻點，j=1，…，J；k=1，…，K表示頻域快拍數。aiq（fj）為從目標源q到陣元i之間的頻率響應。sq（k，fj），ni（k，fj）分別為sq（t）和ni（t）的短時傅里葉變換。由此可以得到第j個頻點的陣列頻域觀測數據快拍矩陣［12］：

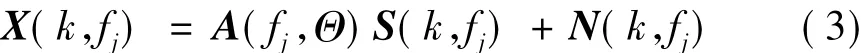
其中：X（k，fj）=［x1（k，fj），…，xN（k，fj）］T為陣列觀測數據矩陣，S（k，fj）=［s1（k，fj），…，sQ（k，fj）］T為源信號矩陣，N（k，fj）=［n1（k，fj），…，nN（k，fj）］T為加性噪聲矩陣。A（fj，Θ）=［aθ1（fj），…，aθQ（fj）］T表示陣列流形矩陣，其中aθ（fj）為：

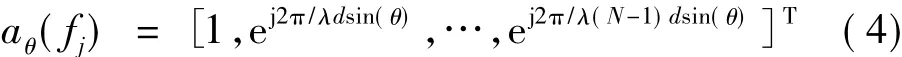
1.2 基于時間結構的非參數盲源分離算法

根據文獻［13］和式（3）可知，傳統瞬時盲源分離算法通過求取解混矩陣來完成對目標源的分離和混合系統的辨識，即：

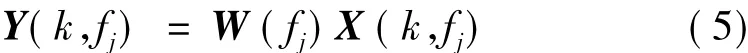
其中：Y（k，fj）=［y1（k，fj），…，yN（k，fj）］T為恢復出的目標源信號。W（fj）表示解混矩陣。

圖1為本文所提算法框架。如圖1所示，利用每個子帶內估計的解混矩陣W（fj）和目標源信號Y（k，fj），求取目標方位能量譜，最后將所有子帶內方位能量譜累加，即可得到總的寬帶方位能量譜。

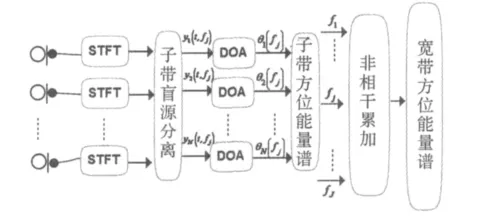
圖1 算法框架Fig.1 The framework of the algorithm

文獻［11］介紹了利用觀測數據的時間結構特性進行盲源分離的思想，其代價函數：

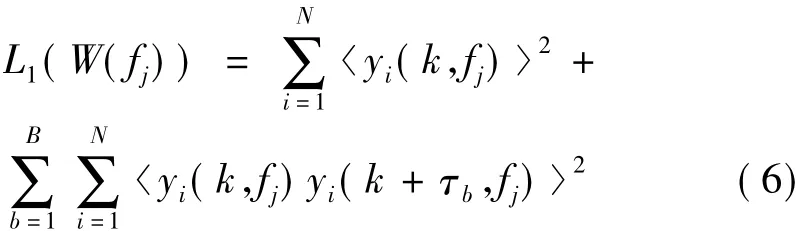
其中：τb，b=1，…，B表示頻點fj處的第b個時間延遲量，又稱時滯量。

根據文獻［13］，利用得到基于信息論準則的盲源分離代價函數：

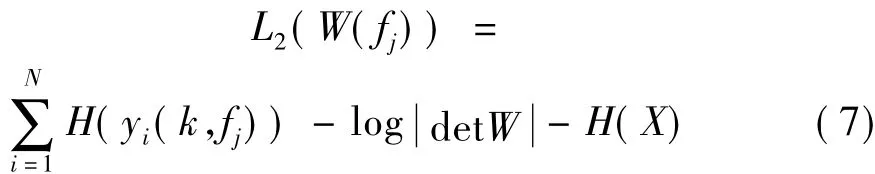
其中：H（·）表示信息熵，H（X）為關于解混矩陣W的常量。

將式（6）與式（7）所表示的代價函數融合，可以得到基于時間延遲結構的盲源分離最優化問題：

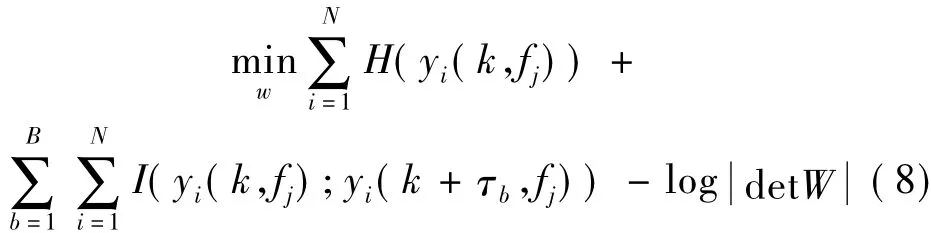
其中：I（yi（k，fj）；yi（k+τb，fj））為：

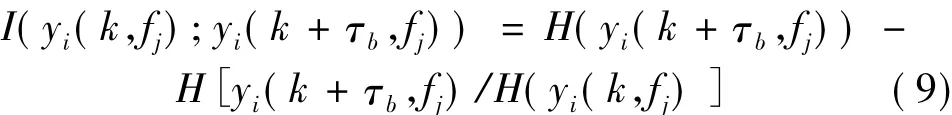
由式（7）和（8）易得式（8）所對應的代價函數：

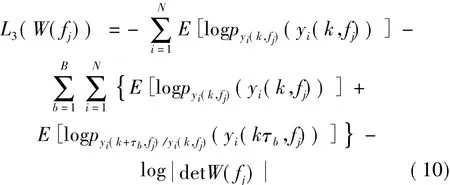
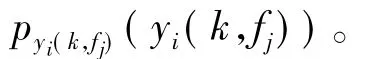
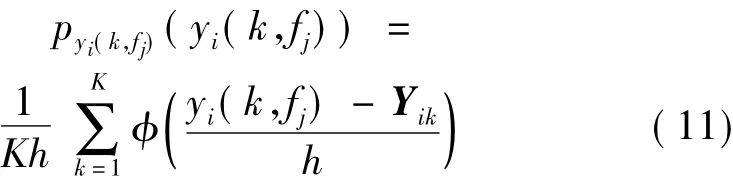
其中：h為內核帶寬［13］，φ（·）為高斯核［13］：

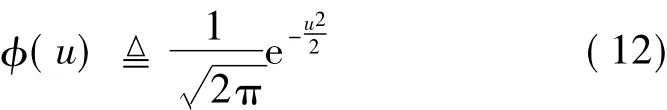
Yim為內核質心［13］：

其中：X（m）（fj）表示每個子帶內觀測數據矩陣的第m個頻域快拍。Wi（fj）表示解混矩陣W（fj）的第i行向量。

根據式（5），則yi（k，fj）=Wi（fj）X（fj），將式（13）代入式（11），可得：

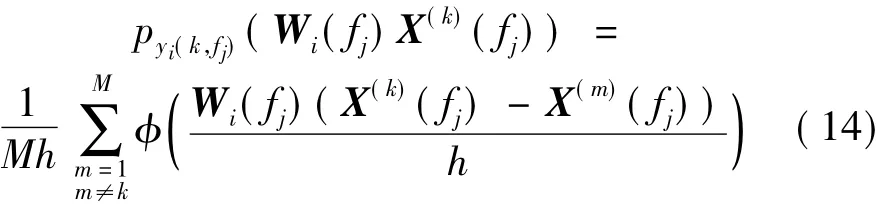
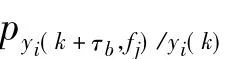
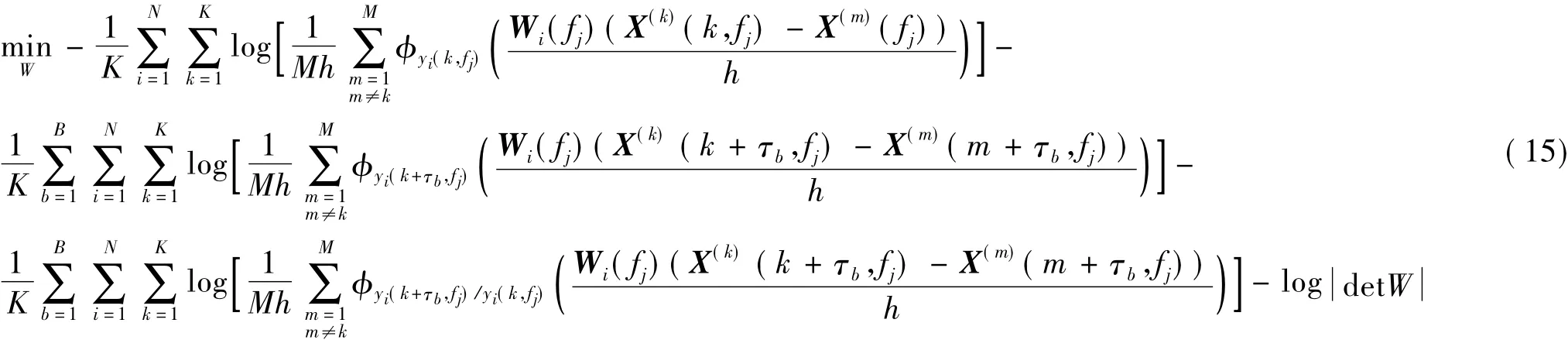
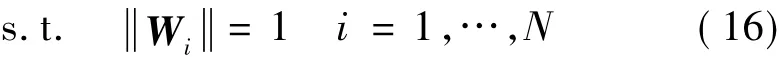
目標函數（15）是解混矩陣W的非線性函數，約束（16）將最優化問題的可能解空間限定到一個有限集內。目標函數（15）可以通過牛頓法對代價函數（10）的非線性最優化解混矩陣Wopt，最優化求解過程同文獻［12］類似。由此估計出的源信號Y（k，fj）=WoptX（k，fj）。

對于盲源分離恢復的結果，每一路輸出的方位都能估計出來：

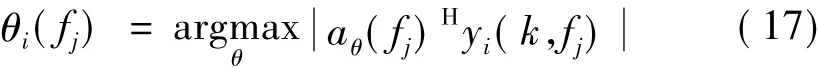
由式（17）在每個頻點fj處估計出的N個θi（fj）值，將每個θi（fj）值在θ=-90°，…，90°方位空間中進行搜索匹配，找到其對應的方位位置，該方位位置的能量值為該路恢復出的源信號的能量。因此可以在每個子帶內構造出類似于波束形成的方位能量譜：

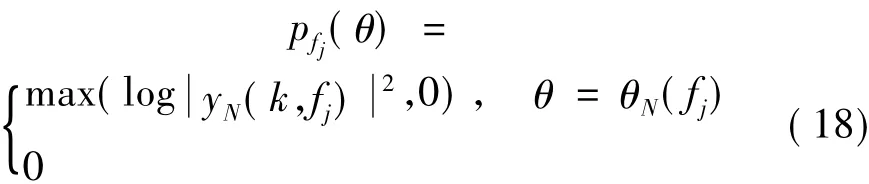
對于式（18）需要說明的是，每個子帶內盲源分離算法估計的N個θi（fj）值有可能會出現重復的情況，本文采取累加的辦法。頻域卷積盲源分離算法普遍存在頻點間次序和頻點尺度模糊的問題。然而式（18）并不受這兩個問題的影響，即使是相鄰頻點間盲源分離輸出次序不一致，對于最后的方位能量譜的構建不構成影響。仿照頻域寬帶波束形成的非相干累加的思想，最后總的方位能量譜為：

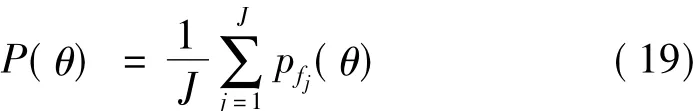
2 數據檢驗

2.1 仿真數據

寬帶仿真實驗考慮均勻線列陣位于兩寬帶目標源的遠場，兩目標源均用海上實錄艦船輻射噪聲代替。兩目標源的原始時域波形與頻譜如圖2所示。寬帶分析頻段為800～1 600 Hz，陣元數為32，陣元間距滿足分析頻段最高頻率對應的半波長。采樣頻率為25 kHz。環境噪聲添加方式使用 MATLAB中 Awgn函數［12］對寬帶陣列數據整體添加加性高斯白噪聲。

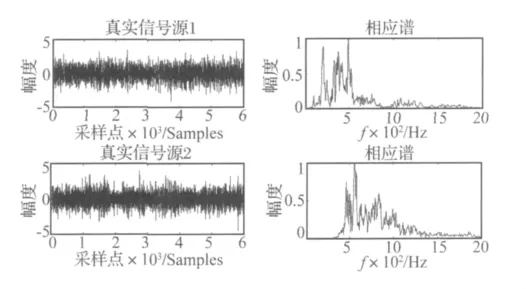
圖2 兩目標源原始時域波形與頻譜Fig.2 The original time domain waveform and frequency spectrum of the two targets

2.1.1 不同信噪比下方位分辨率比較

兩個目標等功率，分析數據長度為1 s，變換不同環境噪聲信噪比（-20 dB～10 dB），采用兩種方位間隔，測試BTSNPSEP與MVDR的方位分辨性能，其中每個信噪比處的估計運行100次蒙特卡洛仿真［12］。圖3為8°目標與11°目標（3°間隔）在不同信噪比條件下的方位分辨性能。圖3（a）為BTSNPSEP方法結果，圖3（b）為MVDR方法結果。比較圖2中兩個子圖可以看出，BTSNPSEP方法在低信噪比時的分辨率要好于MVDR方法。

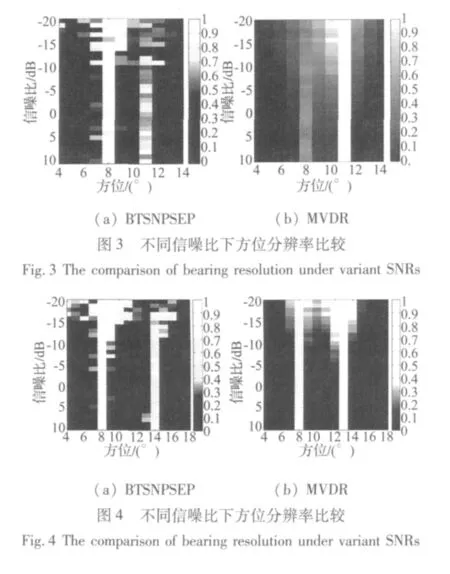
圖4為8°目標與13°目標（5°間隔）在不同信噪比條件下的方位分辨性能。圖4（a）為BTSNPSEP方法結果，圖4（b）為MVDR方法結果。比較圖3中兩個子圖可見當目標間距拉大以后，MVDR的性能變得較好，BTSNPSEP能夠在低信噪比時能夠區分兩個目標，但對于13°目標的估計誤差了1°。

2.1.2 不同目標源數目下方位分辨率比較

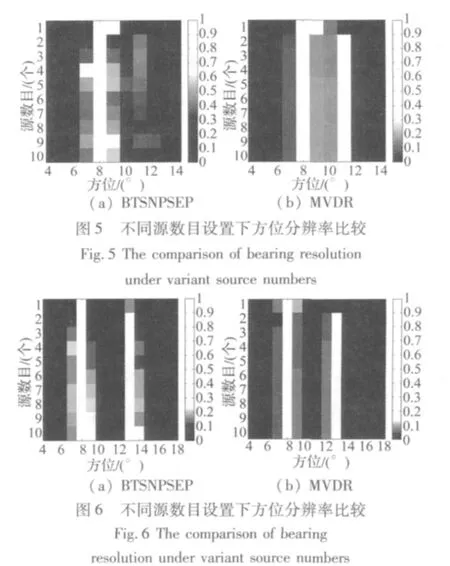
考慮到陣元數較多時的BTSNPSEP方法運算速度問題，通過加入白化預處理步驟［7］，使得BTSNPSEP方法也涉及到源數目設置的問題，由此同MUSIC方法比較不同源數目設置時的方位分辨率。兩個目標依舊等功率，同時環境噪聲信噪比固定為-5 dB，其中每個源數目設置處的估計運行100次蒙特卡洛仿真［12］。圖5為8°目標與11°目標（3°間隔）在不同源數目設置下的方位分辨性能。圖5（a）為BTSNPSEP方法結果，圖5（b）為MVDR方法結果。圖6為8°目標與13°目標（5°間隔）在不同源數目設置下的方位分辨性能。圖6（a）為BTSNPSEP方法結果，圖6（b）為MVDR方法結果。從圖5（a）可以看出，當方位間隔3°時，源數目設置的變化對于BTSNPSEP方法影響還是非常大的，對11°目標的估計不如MUSIC算法。從圖6可以看出當方位間距擴大（5°間隔），BTSNPSEP方法能夠在各種源數目設置下區分兩個目標，尤其是當源數目為1個時（欠定情況）要好于MUSIC。

2.1.3 信干比為-6 dB下弱目標檢測能力

設定8°聲源為干擾源，11°聲源為所需目標源，信干比［12］為 -6 dB，環境噪聲信噪比固定為 -5 dB，BTSNPSEP采用預白化處理源數目設置為3，MUSIC方法同之。共進行20次仿真，每次為100次蒙特卡洛仿真結果。圖7為分別為BTSNPSEP、MVDR、MUSIC三種方法估計結果。比較圖7三個圖可以看出BTSNPSEP對于弱目標的檢測效果要好于MVDR與MUSIC。

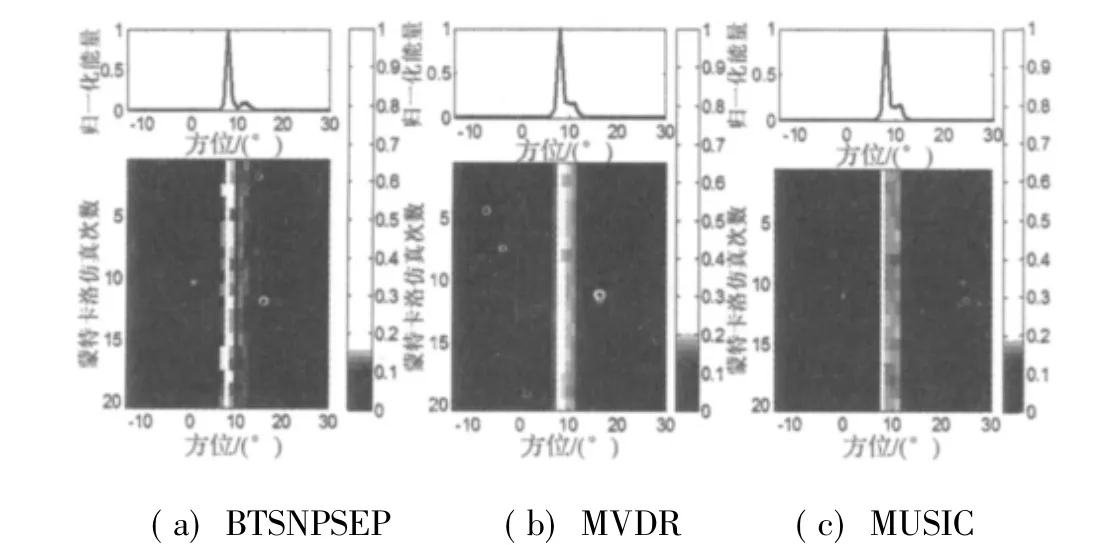
圖7 信干比為-6 dB下弱目標檢測能力比較Fig.7 The comparison of weak target detection capability under SIR=-6dB.

2.2 海上實測數據

試驗海區位于東經121°33＇～121°42＇，北 38°46＇～38°52＇的主航道附近，海區平均水深46 m，聲傳播速度約1 500 m/s。海區地形復雜，水流急，過往船只多，離岸近、干擾源多，屬典型的復雜海區［11］。接收陣列由28個水聽器等間隔組成，陣元間距0.225 m，接收陣列深度約為20 m。水聽器接收信號經信號調理機后到Sony sir1000i錄音機磁帶記錄，整個記錄數據期間，接收船一直輔機發電，有較大噪聲。試驗時目標船在大約5.3 km的距離沿正橫經過接收船［11］。同時，目標船運動時在視覺范圍內還發現有漁船目標運動，而且漁船先于目標船經過接收船正橫。

圖8為三種方法的估計得方位歷程圖比較，其中BTSNPSEP與MUSIC的源數目均設置為20。從圖中可以看出對于-80°～-40°區域的弱干弱目標BTSNPSEP的估計結果相對清晰。第0～100 s時間，對于20°～40°區域的目標船和漁船的估計BTSNPSEP方法也比MUSIC、MVDR方法要清晰，空間增益提高比較明顯。

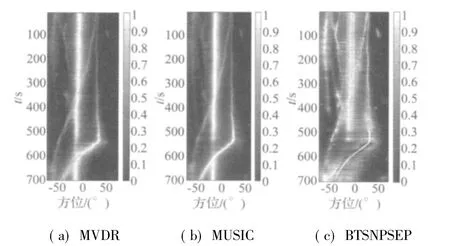
圖8 三種方法海試數據比較Fig.8 The comparison of sea trial result during three methods

3 結論

本文針對被動聲納信號的特殊性，結合兩種盲源分離算法的特點，提出了一種融合時間延遲結構和非參化特性的盲源分離算法（BTSNPSEP），并將其用于被動聲納方位估計。分別利用寬帶仿真和海試數據與經典MVDR和MUSIC高分辨方位估計方法進行了比較，得到以下結論：

（1）BTSNPSEP方法能夠突破瑞利限的限制分辨空間接近的多目標，且在低信噪下的方位分辨性能要好于MVDR方法。

（2）BTSNPSEP方法能夠在欠定條件下分辨出多目標源。

（3）BTSNPSEP方法比起MVDR和MUSIC方法，對于強干擾背景下的弱目標檢測具有一定的優勢。

［1］Meng T Z，Buck J R.Rate distortion bounds on passive sonar performance［J］.IEEE Trans.on Acoustics.Speech and Signal Processing，2010，58（1）：326-336.

［2］ Capon J.High resolution frequency wavenumber spectrum analysis［C］//Proc.of the IEEE，1969，57（8）：1408-1418.

［3］Stoica P，Nehorai A.Music，maximum likelihood，and cram r-rao bound［J］.IEEE Trans.on Acoustics.Speech and Signal Processing，1989，37（5）：720-741.

［4］ Bao C Y.Adaptive beamforming for sonar audio［J］.Proc.of ACOUSTICS 2005.Australia：Australian Acoustical Society Press，2005：483-485.

［5］蔡艷平，李艾華，石林鎖，等.基于盲解卷積的柴油機振動信號分離研究［J］.振動與沖擊，2010，29（9）：38-41.

［6］Benchekroun N，Mansour A.A general structure for the separation of underwater acoustic signals［C］//Proc.of Symposium on Communications，Control and Signal Processing.Marrakech：IEEE Press，2006：273-278.

［7］De Moura，Seixas N N，Filho J M.Independent component analysis for optimal passive sonar signal detection［C］//Seventh International Conference on Intelligent Systems Design and Applications.Rio de Janeiro：IEEE Press，2007：671-678.

［8］雷衍斌，李舜酩，門秀花，等.基于自相關降噪的混疊轉子振動信號分離［J］.振動與沖擊，2011，30（1）：218-222.

［9］張安清.盲分離技術及其在水聲信號中的應用研究［D］.大連：海軍大連艦艇學院，2006.

［10］Saruwatari H，Kurita S，Takeda K.Blind source separation combining independent component analysis and beamforming［J］.EURASIP Journal on Applied Signal Processing，2003，1135-1146.

［11］康春玉，章新華，韓 東.盲源分離與高分辨融合的DOA估計與信號恢復方法［J］.自動化學報，2010，36（3）：443-445.

［12］章新華，范文濤.波束形成與獨立分量分析融合的寬帶高分辨方位估計方法［J］.聲學學報，2009，34（4）：175-180.

［13］ Boscolo R，Pan H，Roychowdhury V P.Independent component analysis based on nonparametric density estimation［J］.IEEE Trans.on Neural Networks，2004，15（1）：55-65.

［14］范 濤，李志農，岳秀廷.基于變分貝葉斯算法和MLP網絡的后非線性混合盲源分離方法研究［J］.振動與沖擊，2010，29（6）：21-24.