水下目標在水下爆炸作用下的毀傷指標研究

李 萬，張志華，梁勝杰，胡俊波

(海軍工程大學 兵器工程系，武漢 430033)

炸藥在水下爆轟瞬間產生的能量可以使爆炸產物氣泡瞬時達到高溫高壓，產生的沖擊波、氣泡和壓力波等會對水下目標造成毀傷。因此人們十分關注水下爆炸對水下目標的毀傷效果的研究，其研究成果廣泛應用于民用和軍事領域，如在民用上通過水下檢測儀器的抗毀傷研究，可以確定臨近水下設施的安全距離；在軍事上通過研究艦船的抗毀傷［1－2］，可以確定船體的薄弱環節從而進行改進；而深入研究水下目標的抗毀傷，不僅在反艦作戰時，能有效增強水中兵器抗毀傷能力，同時也能在反水中兵器攻擊中發揮重要作用。

對水下爆炸比較系統的研究可以追溯到庫爾于1949年出版的《水下爆炸》［3］，該書論述了水下爆炸的基本物理現象以及傳播機理。隨著計算機的高速發展，采用建立動力學方程并進行數值計算，模型試驗和數值計算［4－6］成為研究者常用的研究手段，這樣可以節省試驗經費提高效率。黃曉明等［7］對建立的箱型梁模型在近距水下爆炸作用下的中垂破壞模式進行了試驗研究，張振華等［8］利用有限元程序MSC.DYTRAN中強大的流固耦合功能研究船體的結構毀傷，牟金磊等［9］利用有限元軟件ABAQUS/EXPLICIT計算固支方板破口大小。然而，在實際之中，特別是水下目標，人們積累的經驗很少，邊界條件難以確定以及毀傷機理十分復雜，利用數值仿真難以實現，為避免數值計算，研究者常采用毀傷指標來描述目標的毀傷效果，姚熊亮等［10－12］采用不同的沖擊因子指標來分析結構毀傷情況；張志華等［13］根據試驗獲得的加速度峰值指標，利用統計的方法對目標毀傷的有效性問題進行定量分析，給出了目標毀傷曲線。為了描述毀傷效果，還有利用沖擊波速度峰值、沖擊波壓力峰值等指標來表征毀傷程度，但針對不同的毀傷目標，如何客觀全面的選擇有效毀傷指標集是目前急需解決的問題。

本文針對某水下目標傳感器毀傷的抗爆炸試驗數據，通過對其毀傷指標如加速度峰值和速度峰值指標的分析，研究這些指標之間的相關關系，在此基礎上進一步利用高維壓縮方法，確定影響水下目標毀傷的主要特征指標集，揭示水下目標毀傷的影響機理，為客觀全面準確地描述毀傷效果奠定基礎。

1 水下目標的抗毀傷爆炸試驗

1.1 水下爆炸對目標毀傷的毀傷指標

水下爆炸對水下目標的殺傷機制研究主要是依靠水下爆炸沖擊波載荷對其外殼或傳感器造成沖擊毀傷，使傳感器失靈而失效。

炸藥在水下爆炸時，通常產生沖擊波、氣泡和壓力波。高溫高壓氣泡強烈擠壓周圍的水并向外擴散，于是便形成了初始沖擊波。沖擊波傳播的同時還會伴隨有氣泡的脈動作用，并產生二次壓力波，也會對目標造成破壞作用。但是由于脈動壓力幅值較小，且作用時間較長，在爆炸瞬態動力響應分析時，氣泡脈動產生的影響可不予考慮。與此同時，爆炸破片速度在水中衰減得很快，它也很難在一定距離上對水下目標造成毀傷。所以水下爆炸對水下目標的毀傷主要依靠沖擊波［14］。

針對某種傳感器而言，在水下爆炸的沖擊作用時，由于其外殼的防護作用，如果想通過沖擊波在水下傳播、流固耦合和空氣傳播的過程建立動力學方程進行數值求解將會非常困難，此時需要選擇合適的毀傷指標來分析目標的毀傷效果。傳感器在沖擊作用時會造成如根部脫掉、底座螺釘松動、聯接點斷裂、元器件失效、波形產生漂移和電路板移位等多種毀傷模式，為正常反映傳感器受沖擊和振動的數據，一般選擇測量傳感器加速度和速度［15］作為毀傷指標來反映水下目標受沖擊的程度。加速度和速度一般分為軸向、徑向和周向3個方向，為全面描述反映傳感器毀傷效果，在實驗中選擇這3個方向的加速度峰值和3個方向的速度峰值作為需要測量的數據。

1.2 試驗方案和數據收集

試驗在大型水下爆炸試驗水池中進行，考察小藥量炸藥的水下爆炸對某水下目標的毀傷效果。該水池水面直徑85 m，池底直徑10 m，水深15 m，呈倒圓臺型。將目標固定在水下8 m處。考慮到工程實際，在試驗中的藥包以2 kg球鑄裝TNT藥包作為標準藥包，由于是小藥量炸藥爆炸，本試驗中的自由表面和水底的影響可忽略，可近似認為炸藥在無限、均勻、靜止的水介質中爆炸。

根據爆炸理論和實際經驗可認為影響目標損壞的主要因素是TNT質量、水深、爆炸距離R、方向角α等。本試驗固定了其它主要影響因素水平，僅考慮爆炸距離R和方向角α(藥包與目標中心連線和目標軸線的夾角，也稱爆炸角度)影響因素。實驗時在目標內的元件底板上布設一個安裝塊，在相互垂直的3個方向各安一個加速度傳感器，并計算獲得3個方向的速度值。為了比較各次試驗的毀傷效果，共進行了11次試驗，測得目標處的3個加速度峰值和計算得到的3個速度峰值，判別了目標毀傷效果，為分析方便進行歸類和編號，試驗結果中，有7次目標未發生毀傷，4次目標發生毀傷，如表5。

2 因子分析方法

因子分析法是通過尋找公共因子來綜合反映全部指標的大部分信息的統計方法，找出與公共因子載荷較大的原始指標作為特征指標，利用選擇的特征指標分析問題其可信度仍然很高。

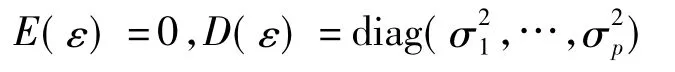
假定隨機向量X滿足以下的模型：

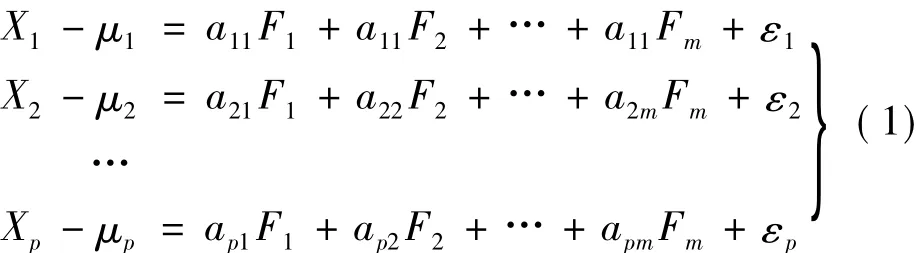
則稱模型(1)為正交模型，用矩陣表示為：

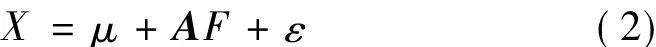
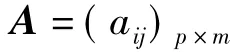
基本步驟：

(1)設x是具有p維(列)向量元素的隨機向量。x(1)，x(2)，…，x(n)是隨機向量x的n個樣本。將原始數據進行標準化處理，消除量綱的影響。

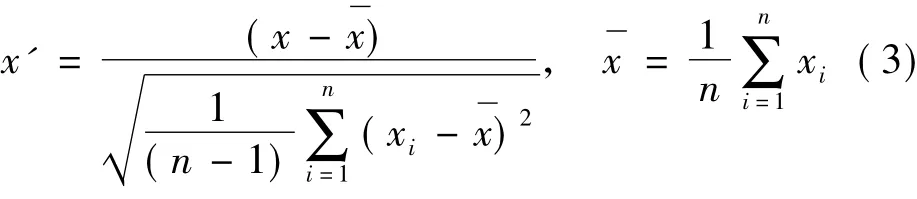
(2)計算x的相關系數矩陣Cx=E{x'x'T}；利用相關函數進行相關性分析。

將每一個指標看做關于n的時間序列值，則第i個指標表示為：xi(n)。利用第i個指標與第j個指標之間的相關函數，可判斷兩者相關性的強弱。相關函數為：

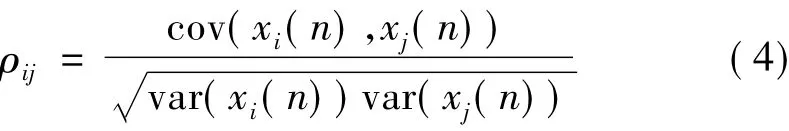
其中，var(xi(n))、var(xj(n))分別是 xi(n)、xj(n)的方差，cov(xi(n)，xj(n))是 xi(n)、xj(n)的協方差。

(3) 計算矩陣 Cx的特征值 λ1，λ2，…，λp(λ1≥λ2≥…≥λp)，并根據累積貢獻率：

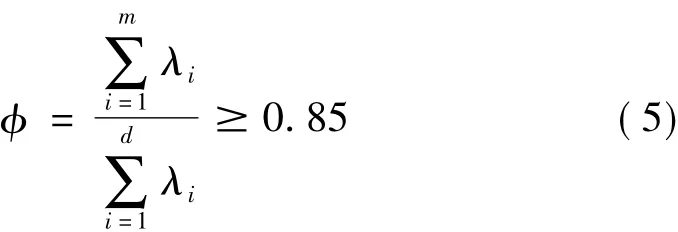
確定m取值，找出前m個公共因子。

(4)計算因子載荷矩陣。

(5)對因子載荷矩陣進行旋轉變換，得到方差極大正交旋轉因子載荷陣。

為了使因子有明顯的含義，需對因子載荷矩陣進行正交旋轉，則在保持各指標的公因子方差不變的條件下使載荷矩陣通過旋轉變換使因子載荷矩陣每一列各元素向0和1兩極分化，突出每個公共因子和其載荷較大的原始指標的聯系，從而可選擇出特征指標。

(6)將因子變為原始指標的線性組合，計算因子值。具體計算步驟見文獻［16］。

3 數據處理

3.1 相關性分析

在對目標毀傷效果進行定量分析時，將以實驗測得的軸向加速度峰值X1、徑向加速度峰值X2、周向加速度峰值X3、軸向速度峰值X4、徑向速度峰值X5、周向速度峰值X6六個變量為原始指標進行相關性分析。

利用相關函數對這些指標進行相關性分析，如表1。

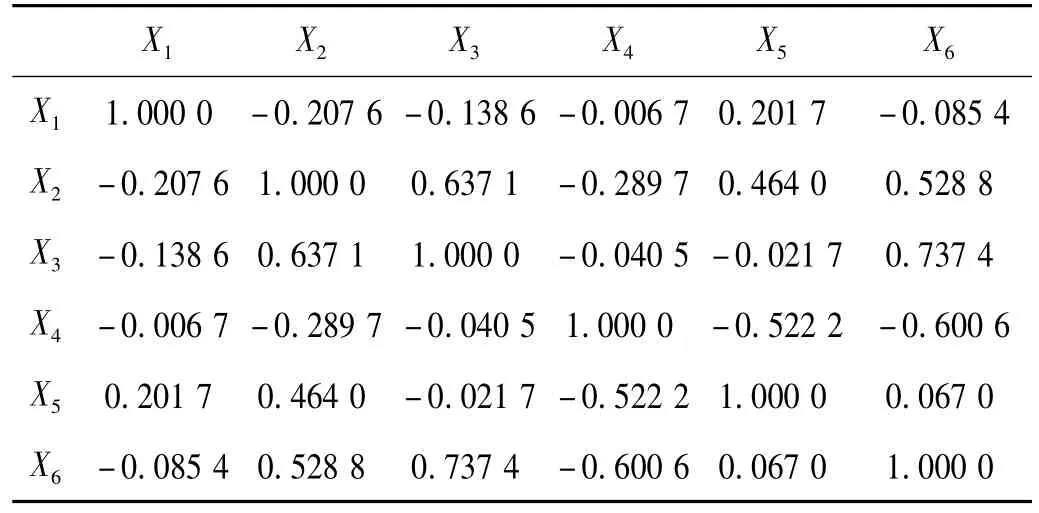
表1 六個原始指標之間的相關函數值Tab.1 Correlative function data of character variable among the six primitive indexes

(1)加速度峰值指標之間。徑向加速度峰值X2與周向加速度峰值X3線性相關值為0.637 1，有較大的線性正相關。軸向加速度峰值X1與徑向加速度峰值X2、周向加速度峰值X3的線性相關值都很小。X1與X2幾乎不存在線性相關。

(2)速度峰值指標之間。軸向速度峰值X4與徑向速度峰值X5，軸向速度峰值X4與周向速度峰值X6的線性相關值都較大，分別為－0.522 2和－0.600 6，有較大的線性負相關。而軸向速度峰值X4與周向速度峰值X6的線性相關值為0.067 0，不存在線性相關。

(3)各個方向上加速度峰值指標與速度峰值指標之間。軸向加速度峰值X1與軸向速度峰值X4不存在線性相關，徑向加速度峰值X2與徑向速度峰值X5為較大線性相關，周向加速度峰值X3與軸向速度峰值X6的線性相關值高達0.737 4。

由上面分析可知各個指標間有較強的相關性，說明這些數據之間信息有重疊，為找出影響目標毀傷的主要指標，本文使用因子分析方法選擇特征指標。

3.2 特征指標的分析與選擇

對數據進行因子分析，前4個因子的累積方差貢獻率為96.79%，說明這4個因子已包含了關于原始指標的主要信息，故確定公共因子為 F'1，F'2，F'3，F'4，如表2，得到的因子載荷陣如表3。

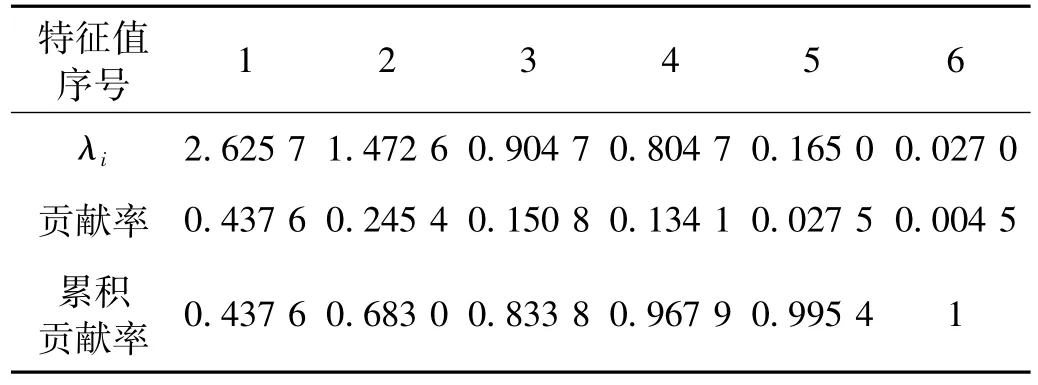
表2 公共因子的特征值和貢獻率Tab.2 Contributing ratio of public factors

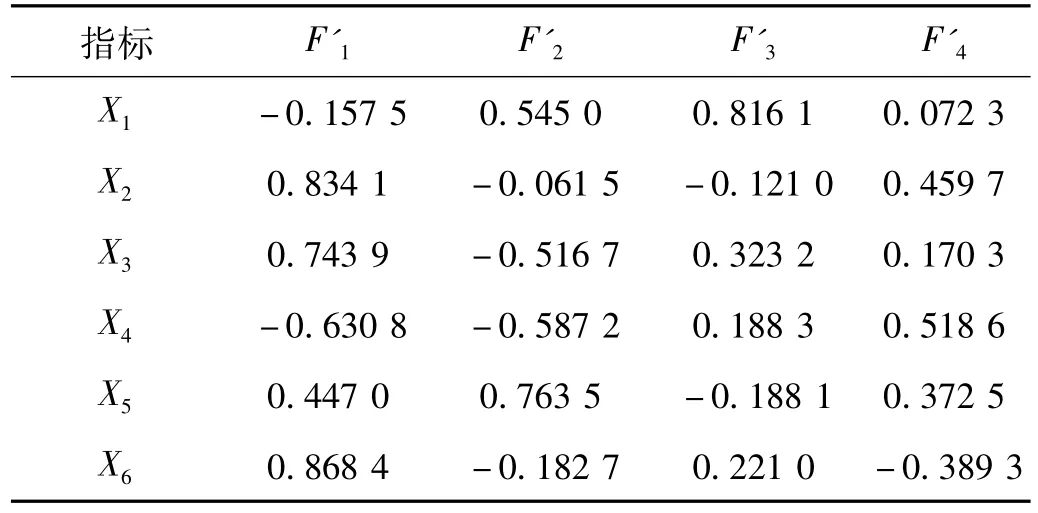
表3 因子載荷陣Tab.3 Factor loading matrix

由于公共因子載荷中出現了相當多的中等載荷，使各個公共因子的含義含糊不清，不利于對因子進行解釋。公共因子載荷陣經過方差極大正交旋轉以后，所得出的正交因子載荷矩陣如表4所示。在正交因子載荷矩陣中，每個因子對于各個指標的載荷有了明顯的差異，對同一個因子而言，載荷向兩極分化，中等載荷傾向于消失，這就大大有利于分析解釋公共因子和其載荷較大的那些指標的聯系，有利于將特征指標提取出來，并且經計算各個指標的共同度都達到92%以上，反映了原始指標對公共因子F的依賴程度高。

(1)公共因子代表了原始指標的大部分信息，所以與公共因子載荷越大的原始指標，包含了目標毀傷的大部分信息。軸向加速度峰值X1與軸向速度峰值X4分別和公共因子F4與F2因子載荷達到了0.992 4和0.941 6。周向加速度峰值X3與徑向速度峰值X5分別和公共因子F1與F3的因子載荷達到了0.973 1和0.931 1，由此可知 X1、X3、X4和 X5相對于 X2、X6對目標毀壞的影響更大。

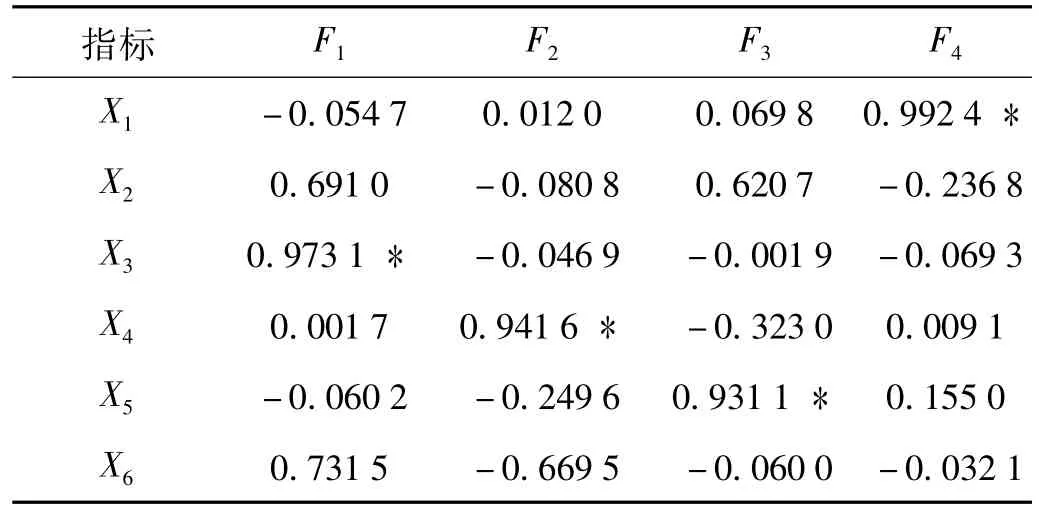
表4 方差極大正交旋轉因子載荷陣Tab.4 Factor loading matrix of orthogonal varimax rotation for the data

公共因子的特征量越大代表了方差越大，也即代表了這個公共因子所包含信息越多。公共因子F1比F2，F3，F4的特征值大很多，說明X3所包含的信息最多，而F2相對綜合了X4和X6兩個指標的信息，F3相對綜合了X2和X35兩個指標的信息，雖然F4的特征值最小，但它相對只綜合了X1的信息，從一定程度上F4比F2與F3更重要。

(2)F2，F3，F4這三個公共因子的特征值相差不大。F1除了代表X3信息外還與X2、X6的載荷很大，而X2與代表X5信息的F3的載荷很大，X6與代表X4信息的F2載荷很大，說明F1在一定程度上反映了F3和F2的信息。并且F4與除X1的其它原始指標的載荷都很小，也即與F1，F2，F3所反映的信息重疊得不多，故選擇F1與F4作出得分圖1。根據虛線除了第6次試驗外能較好的區分目標毀傷類和非毀傷類，而F1與F4主要代表了X3與X1的信息，所以X3與X1相對于X4和X5能更好地表征目標毀傷效果。而且由3.1節的相關性分析知X1與X3幾乎不存在線性相關，于是可選擇軸向加速度峰值X1與周向加速度峰值X3作為特征指標。

(3)傳感器的毀傷模式有很多種，如根部脫掉、底座螺釘松動、聯接點斷裂是由于軸向方向沖擊擠壓所造成；而元器件失效、波形產生漂移、電路板移位是由于徑向方向振動所造成，可見軸向加速度峰值X1與周向加速度峰值X3這兩個指標分別代表了傳感器毀傷的兩種最重要的毀傷模式。

3.3 判別分析

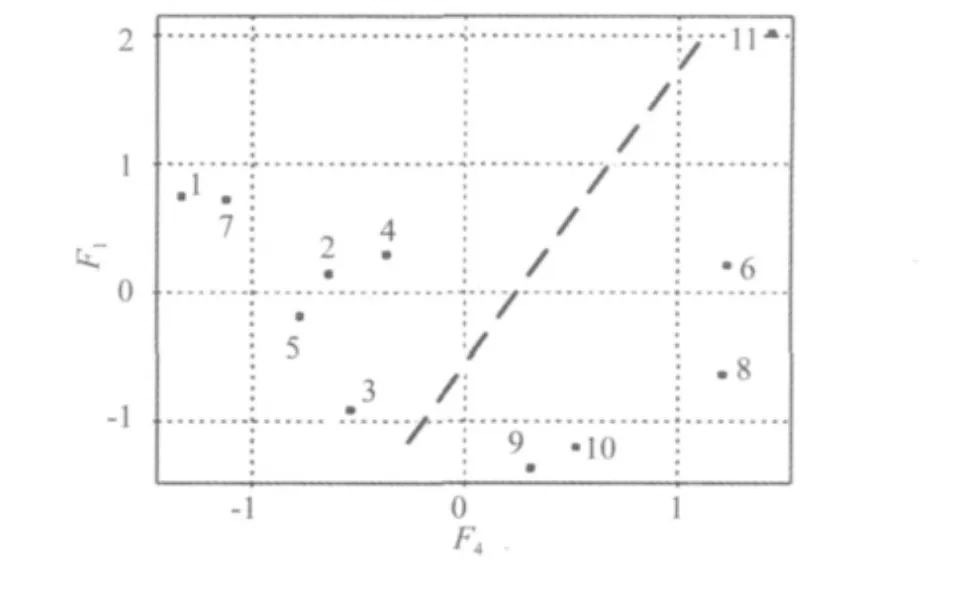
圖1 F1與F4的得分圖Fig.1 The scoring figure of F1and F4

為進一步探討上述用軸向加速度峰值X1與周向加速度峰值X3作為特征指標是否合理，首先選用4個公共因子 F1，F2，F3，F4，利用費歇爾判別法［16－17］對目標毀傷進行判別分析，然后用X1和X3這兩個指標進行費歇爾判別分析，如果判別結果大部分相同，就在一定程度上客觀地表明X1和X3代表了目標毀傷的大部分信息。

先處理第1組數據，為了判別目標是否毀傷，將峰值向量分為2類：不能使目標毀傷峰值向量和能夠使目標毀傷的峰值向量，可以建立水下目標毀傷費歇爾判別模型：

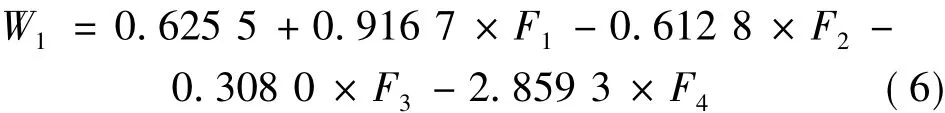
其中 F1，F2，F3，F4由 3.3 節利用因子分析法數據重構而來。根據提出的水下目標毀傷費歇爾判別模型，將11次試驗的指標值代入這兩個判別函數模型，若W1＞0大，則歸入未毀傷類；若W1＜0大，則歸入毀傷類。

同樣對第2組也進行費歇爾判別分析得到判別模型：

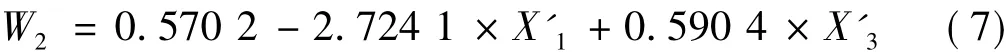
其中X'1，X'3是X1，X3的標準化數據。再按上面方法進行歸類，如表5。

(1)從表5的判斷結果可以看出，兩個判別模型判斷結果都與實際結果一致的有10個，正確率達到90.9%，只有第6號試驗的判斷結果與實際試驗結果不一致。對這個判斷出現錯誤的試驗進行分析發現：對于第6號試驗，試驗結果盡管是傳感器未毀傷，但在通電檢查中出現誤動現象，說明傳感器已達到臨界毀傷狀態。而且這個結果與3.2節中分析的一致。

(2)通過這兩組數據判別分析對比結果來看，只利用原始指標X1，X3進行判別分析的結果與用因子分析法重構數據F1，F2，F3，F4進行判別分析的結果一致，這就充分說明了X1，X3包含了目標毀傷的絕大部分信息，選用軸向加速度峰值X1與周向加速度峰值X3作為特征指標是合理的。

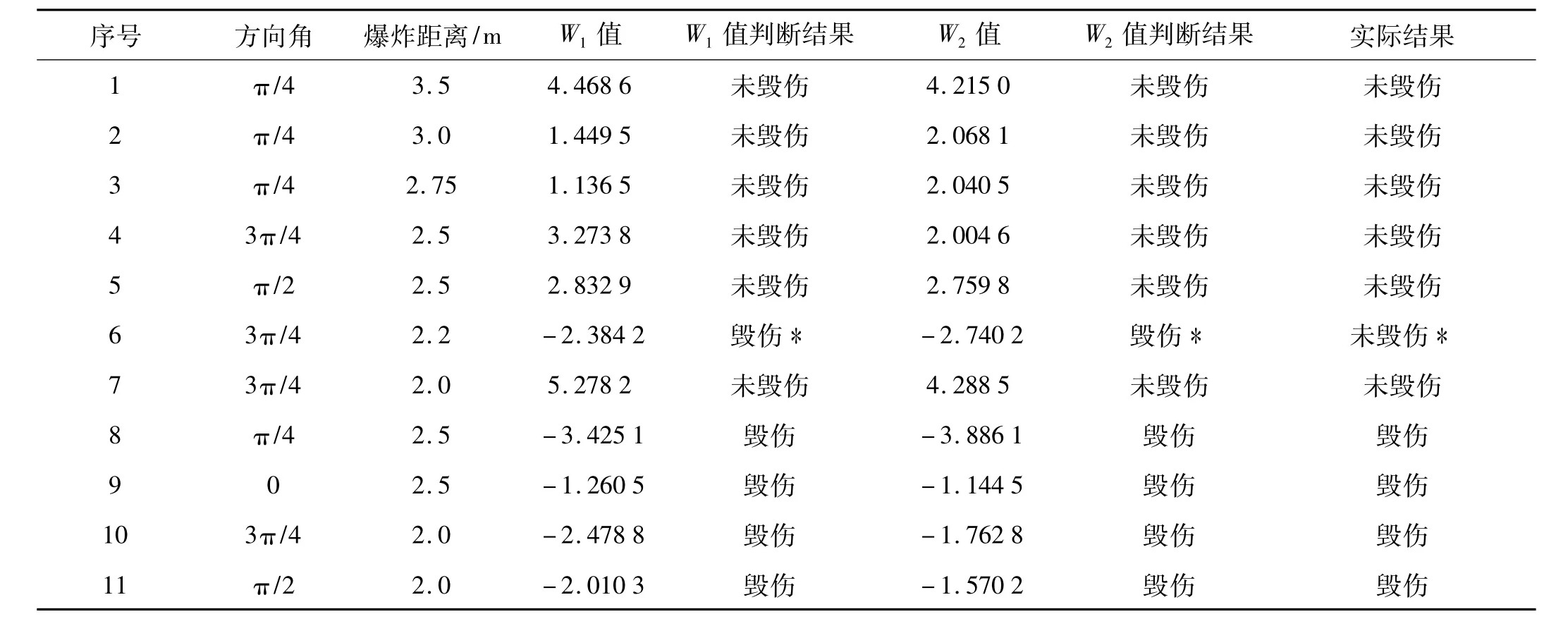
表5 不同方向角和爆炸距離的目標毀傷效果Tab.5 Damage results of the target at different direction angle and explosion distance

4 結論

(1)針對某水下目標傳感器毀傷的抗爆炸試驗數據，通過用相關函數法對加速度峰值和速度峰值指標進行相關分析，表明這些指標之間相關值很大，在此基礎上進一步利用因子分析法，確定了影響水下目標毀傷的特征指標集軸向加速度峰值X1與周向加速度峰值X3，并利用費歇爾判別法證明了選用這兩個指標作為特征指標是合理的。

(2)一方面研究者在選擇影響水下目標毀傷指標測量時可以只選用這兩個指標。另一方面在設計內部傳感器時軸向和周向兩個方向上時既要由良好的抗沖效果外同時也要有良好的減振效果。

［1］劉建湖.艦船非接觸水下爆炸動力學的理論與應用［D］.無錫：中國船舶科學研究中心，2002.

［2］劉潤泉，白雪飛，朱 錫.艦船單元結構模型水下接觸爆炸破口試驗研究［J］.海軍工程大學學報，2001，13(5)：41－46.

［3］Cole.Underwater explosions［M］.Princeton：Prince-ton University Press，1948.

［4］Hammond L，Grzebieta R.The requirement for hydrostatic initialization in LS-DYNA/USA finite element models［J］.Shock and Vibration，2000，7(2)：57 －65.

［5］Cho C L，Yuh S T.Shock response of a surface ship subjected to noncontact underwater explosions［J］.Int J Impact Engng，2006，33：748 －772.

［6］李 健，榮吉利.水下爆炸圓柱殼塑性動態響應實驗及數值計算［J］.北京理工大學學報，2008，28(8)：659 －662.

［7］黃曉明，朱 錫，牟金磊，等.近距水下爆炸作用下箱型梁模型中垂破壞試驗研究［J］.振動與沖擊，2011，30(2)：19－23.

［8］張振華.艦艇結構水下抗爆能力研究［D］.武漢：海軍工程大學，2004.

［9］牟金磊，朱 錫，黃曉明，等.水下近場非接觸爆炸作用下固支方板破口計算［J］.振動與沖擊，2011，30(1)：37－39，55.

［10］姚熊亮，曹 宇，郭 君，等.一種用于水面艦船的水下爆炸沖擊因子［J］.哈爾濱工程大學學報，2007，28(5)：501－509.

［11］姚熊亮，郭 君，曹 宇，等.在水下爆炸沖擊波作用下的新型沖擊因子［J］.中國造船，2008，49(2)：52 －60.

［12］姚熊亮，許維軍，梁德利.水下爆炸時艦船沖擊環境與沖擊因子的關系［J］.哈爾濱工程大學學報，2004，25(1)：6－12.

［13］張志華，鐘強暉，李慶民.小藥量水下爆炸對水下目標的毀傷有效值評估［J］.兵工學報，2009，30(10)，1344 －1348.

［14］姚熊亮，楊樹濤，張阿漫，等.水下爆炸載荷作用下魚雷結構優化設計［J］.艦船科學技術，2009，31(4)：75 －80.

［15］王貢獻，褚德英，張 磊，等.艦船設備沖擊試驗機研究進展［J］.振動與沖擊，2007，26(2)：152 －159.

［16］高惠璇.應用多元統計分析［M］.北京：北京大學出版社，2005.

［17］余 頌，陳善雄，余 飛，等.膨脹土判別與分類的Fisher判別分析方法［J］.巖土力學，2007，28(3)：499－504.