速度剪切流中圓柱體繞流特性的數值模擬

周 強，曹曙陽，王 通，周志勇

（同濟大學 土木工程防災國家重點實驗室，上海 200092）

自然界的風場主要有良態風場和特異風場。現行的橋梁與結構抗風設計方法主要是針對常規良態風場，而實際風災害絕大多數是由極端風氣候、突變風等特異風引起的，如龍卷風、臺風、下擊雷暴風等。特異風通常具有強速度剪切特性、特殊風速剖面、強旋轉氣流以及復雜的時空分布特性。目前國內針對特異風的研究很少。瞿偉廉等［19］通過數值方法模擬了作用在某輸電塔結構上的下擊暴流荷載時程。趙楊等［18］利用主動控制風洞模擬出了雷暴沖擊風陣風剖面（如圖1所示）；然后，采用“階躍流法”模擬了風速突變的時程；最后將高層結構模型置于該突變氣流中，觀測在特殊氣流中結構表面風壓以及結構空氣動力學參數的變化特征。本文針對其中風速剪切特性，對置于剪切流中的圓柱體氣動力特性、尾流特性展開研究。

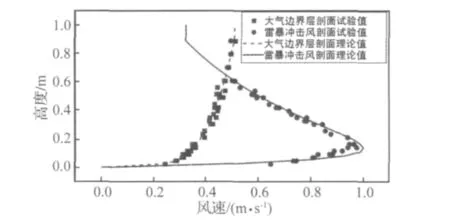
圖1 雷暴沖擊風風速剖面理論和試驗值［18］Fig.1 The wind profile of thunderstorm and Boundary layer

目前針對考慮速度剪切效應的圓柱體繞流問題的研究主要集中在航空航天領域，但由于其所關心的問題是升阻比，和風工程存在差異，因此需要從風工程角度對置于剪切流中的圓柱體繞流問題進行研究。在這方面國外學者已有一些試驗研究，Adachi和Kato［1］研究了在 Re=2.67×103～1.07×104和0＜β＜0.05范圍內的圓柱體繞流問題，結果表明阻力和升力都隨著β的增加而增加，且升力的方向是由高速側指向低速側。Hayashi和 Yoshino［4］對在 Re=6 ×104，β=0.25 的流場中的圓柱氣動力問題進行了研究，發現阻力相比于均勻流是減少的，但升力方向仍然是由高速側指向低速側。Sumner和 Akosile［12］在小的剪切參數范圍（0.02 ＜β＜0.07）和雷諾數 Re=4.0 ×104～9.0 ×104條件下的研究發現阻力與升力的結果和Hayashi和Yoshino［4］的結果基本相同。但是目前對這一問題的數值模擬研究較少，且都是進行二維的計算。Tamura等［14］對處于Re=40，80，0 ＜β＜0.20 的剪切流中的圓柱體繞流問題進行了數值模擬研究。Lei等［9］采用上游差分法對Re=50～160，0＜β＜0.2的流動進行了二維數值模擬。Lei和Tamura都預測在剪切流中前端的駐點位置會向高速側移動；但是Lei的結果表明升力方向是指向低速側的，而Tamura則認為是相反的方向。由此可見，對這種流場還有許多問題沒有澄清，因此很有必要采用三維數值模擬方法對其進行進一步的細節研究。

本文針對上述4個氣流特點中的風速剪切特性，對置于剪切流中的圓柱體氣動力特性展開研究，并且引入剪切參數β表示速度剪切強度，β=G（D/Uc），其中G是速度梯度，D是圓柱直徑，Uc是圓柱正前方來流的平均風速，如圖2所示。雷諾數為Re=UcD/ν，因此當Uc不變時，可以通過改變速度梯度G來改變剪切參數，即可以在雷諾數不變的情況下改變剪切參數。本文計算的雷諾數分別為 Re=60，80，150，200，220，500 和 1 000，其中當 Re=60，80，150，200和220時采用三維直接數值模擬（DNS），Re=500和1 000時采用基于Smagorinsky動態亞格子模型的三維大渦模擬（LES）。本文主要研究氣動力特性隨剪切參數β和雷諾數的變化情況，并分析產生這些氣動現象的物理機理。

圖2 剪切流示意圖Fig.2 Schematic of shear flow configuration

1 控制方程與建模

1.1 控制方程

本文采用廣義曲線坐標系來表示流體控制方程。DNS的連續性方程和N-S方程如式（1）和（2）所示：

式中：

式中：J為物理空間和計算空間之間Jacobian行列式，Um為廣義曲線坐標下的逆變速度分量，Gmn為網格劃分的偏度張量。

LES的連續性和N-S方程為：

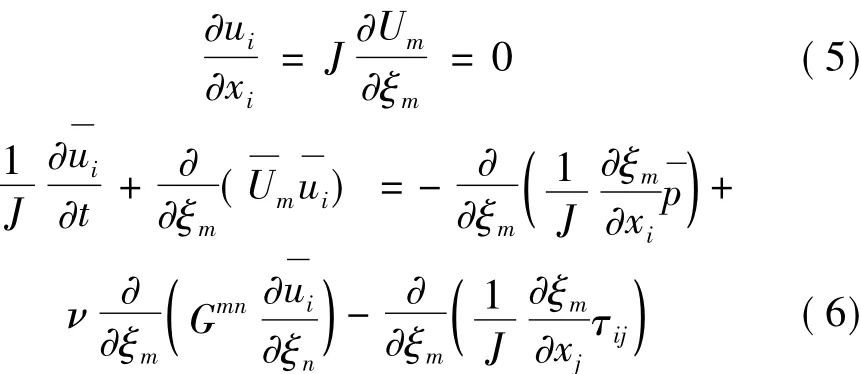
式中：～表示測試過濾操作。如Germano等［3］建議的，這里唯一的參數——測試過濾與格子過濾比率取2.0。同時為避免出現數值不穩定，在計算中負的SGS渦粘性系數取為0。

1.2 網格劃分和算法

本文用Zang等［13］開發的基于 Co-located網格的數值模擬方法，在曲線坐標系下，求解三維非定常不可壓縮N-S方程。在計算空間中，以控制體的中心作為定義點來定義速度分量和壓力，而以相應的單元壁面中點為定義點來定義體積通量。用四階中心差分和四階中心插值離散對流項，用二階中心差分和二階中心插值離散擴散項。關于時間發展，對流項采用Adams-Bashforth差分格式，而擴散項則采用半隱式的Crank-Nicolson格式。

首先，笛卡爾坐標系下中間速度分量可由式（11）得到：

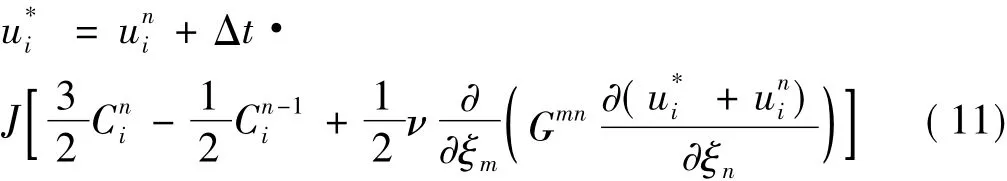
通過坐標轉換可以得到單元中心的逆變速度分量，從而插值得到單元壁面上的逆變速度分量。采用SOR法求解Poisson方程得到下一步的勢場：

然后，本文可以根據式（13）、式（14）得到笛卡爾坐標系的速度分量和逆向速度分量：

上述算法已廣泛應用于湍流場的數值模擬中。

1.3 數值模型和邊界條件

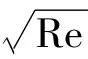
本文采用計算區域及邊界條件如圖3所示。

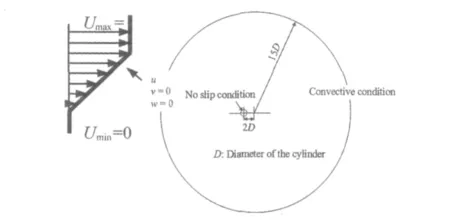
圖3 計算區域和邊界條件Fig.3 Computational domain and boundary conditions

圓柱體表面邊界條件：速度ui無滑移條件和擬壓φ的Neumann條件。

來流邊界條件：如圖2所示，采用速度剪切流作為來流，即U=1+Gy，v=0和w=0；擬壓的Neumann條件。同時為了避免在來流中出現反向流，當y＜-1/G時，來流速度取為0。

展向邊界條件：速度和擬壓應滿足周期性邊界條件。

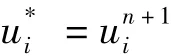
2 數值驗證

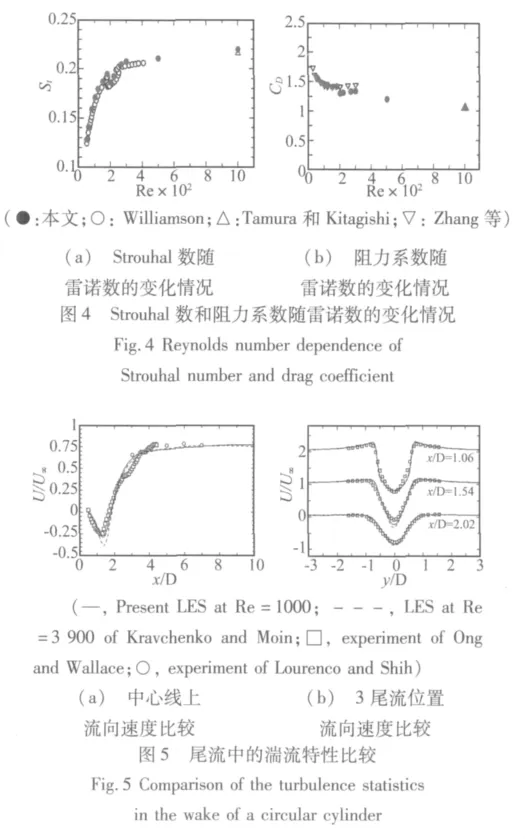
比較圓柱體近端和遠端尾流的一階和二階湍流特性是理想的驗證方法。但由于缺少在這雷諾數范圍內的試驗數據，因此本文首先在Re=50～1 000區域內比較了Strouhal數和阻力系數，結果如圖4所示。然后圖5比較了本文在Re=1 000時得到的湍流特性結果、Kravchenko等［8］用大渦模擬得到的結果（Re=3 900）以及Ong和Wallace［11］等的試驗結果。由此可見，本文進行的直接模擬和大渦模擬是有效和可靠的。

3 數值結果及討論

本節主要研究了速度剪切流對圓柱繞流尾流結構特征及氣動力特性的影響。

3.1 繞流結構特征

圖6給出了在不同的雷諾數下，Strouhal數隨剪切參數的變化情況。可以看出，Strouhal數基本不隨剪切參數變化，其大小只取決于雷諾數的大小。這一結果與 Sumner和 Akosile［12］、Cao 等［2］的試驗結果相一致；與 Lei［9］、Kang［5］的數值模擬結果有細微差別，其原因可能在于他們進行的是二維數值模擬。

圖7給出了瞬時尾流結構隨剪切參數的變化情況，可以發現，高、低速兩側脫落的旋渦的不對性隨著剪切參數的增加而增大，Karman渦脫被抑制。

駐點漂移是剪切流中重要的現象之一，圖8給出了駐點位置隨著剪切參數變化的情況，其中θ0表示駐點位置所對應的圓心角（高速側為正）。可以看出，隨著β的增大駐點位置不斷向高速側移動，且變化基本和β成線性關系。同時還可以從圖9看出，在低雷諾數下，駐點位置隨著雷諾數的增加而顯著改變，但是當Re＞500后，其位置基本保持不變。所以本文認為在較大雷諾數下，駐點位置基本不再受雷諾數效應的影響，而主要由剪切系數β決定。

本文發現一個重要現象——兩側分離點隨剪切參數的變化規律。圖10給出了圓柱體兩側分離點位置隨剪切參數的變化情況。可以看出高速側的分離點向下游移動，而低速側的分離點則向上游移動，且隨著剪切參數呈線性變化。由于駐點和分離點位置的漂移，因此圓柱體周圍流場特征也發生了改變，分離邊界層的強度和厚度以及分離邊界層中產生的旋渦在圓柱兩側也不相同，從而在兩側形成不對稱的流動。這些流場特征都將會影響圓柱體上氣動力的產生，這些本文將在下面進一步討論。

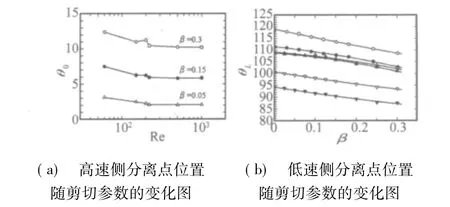
圖10 分離點位置隨剪切參數的變化圖（符號意義同圖6）Fig.10 Variation of separation point with shear parameter

3.2 氣動力特性

作為一個例子，圖11給出了Re=1000時的圓柱體高速側和低速側的壓力系數分布圖。可以看出，兩側的壓力分布不對稱，而且明顯可以發現駐點的位置向高速側移動。同時還可以發現，壓力分布會隨著剪切參數變化。根據兩側壓力的相對大小，可見在從駐點到最小壓力點之間區域（A區），其特點為高速側的壓力更大；在由最小壓力點到分離點之間區域（B區），低速側的壓力更大；在兩側流動的相互作用區域（C區），所以兩側壓力幾乎相同。A區的壓力分布主要是由駐點位置移動引起的；而B區的壓力分布主要是由于整個流場中的速度剪切和分離點位置移動的共同作用而產生的。在其他雷諾數下的壓力分布隨剪切系數的變化情況和Re=1000下的情況基本一致。

圖11 不同剪切參數下的圓柱體周圍壓力分布及其分區Fig.11 Variation of pressure distribution with shear parameter and its zoning

在剪切流中由于壓力分布不對稱性，導致升力產生。在B區，由于速度剪切的影響，低速側的壓力較大，從而產生一個由低速側向高速側作用的升力；而在A區，由于駐點漂移的影響，高速側的壓力較大，從而產生一個由高速側向低速側作用的升力。由于A區的作用更顯著，所以綜合的升力方向是由高速側指向低速側，如圖12 所示。Sumner等［12］、Cao 等［2］的試驗研究，以及Lei等［9］數值模擬也都發現了類似的結論，但由于長寬比和紊流水平的不同，本文與上述文獻中的升力變化率有所不同。

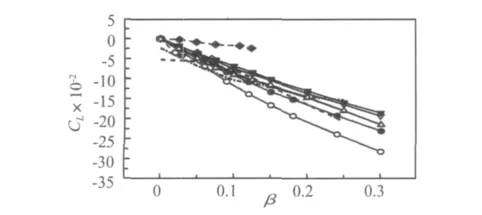
圖12 升力系數隨剪切參數的變化Fig.12 Variation of lift coefficient with shear parameter at different Reynolds numbers

4 結論

本文采用三維直接數值模擬（DNS）和大渦模擬（LES）研究了雷諾數Re=60～1 000范圍內速度剪切特性對圓柱繞流問題的影響，得到以下有益結論：

（1）在剪切流中的駐點向高速側移動，且其對應的圓心角隨剪切參數的增大而增大。

（2）分離點在高速側向下游移動，在低速側向上游移動，且分離點移動的角度隨剪切參數的增加而增大，同時發現雷諾數對分離點移動的影響很大。

（3）駐點以及分離點位置的移動導致圓柱表面壓力發生變化，且這種變化對升力的貢獻要大于兩側速度不對稱性的貢獻，所以升力的作用方向由高速側指向低速側，而且隨著剪切參數的增加，升力系數也隨之增加。

（4）在Re=60～1 000范圍內，Strouhal數基本不隨剪切參數變化，其大小取決于Re數的大小，而且隨著剪切參數的增加，Karman渦脫將會被抑制。

［1］Adachi T，Kato E.Study on the flow about a circular cylinder in shear flow［J］.Transactions of the Japan Society for Aeronautical and Space，1975，256：45-53.

［2］ Cao S，Ozono S，Hirano K，et al.Vortex shedding and aerodynamic forces on a circular cylinder in linear shear flow at subcritical Reynolds number［J］.Journal of Fluids and Structures，2007，23：703-714.

［3］Germano M，Piomelli U，Moin P，et al.A dynamic subgridscale viscosity model［J］.Physics of Fluids，1991，3（7）：1760-1765.

［4］Hayashi T，Yoshino F.On the evaluation of the aerodynamic forces acting on a circular cylinder in a uniform shear flow［J］.Transactions of the Japan Society for Mechanical Engineering，1990，56（552）：31-36.

［5］ Kang S.Uniform-shear flow over a circular cylinder at low Reynolds numbers［J］.Journal of Fluids and Structures，2006，22：541-555.

［6］Kim J，Moin P.Application of a fractional-step method to incompressible Navier-Stokesequations［J］. Journalof Computational Physics，1985，59：308-323.

［7］Kwon T S，Sung H J，Hyun J M.Experimental investigation of uniform shear flow past a circular cylinder［J］.ASME Journal of Fluids Engineering，1992，114：457-460.

［8］Kravchenko A G，Moin P.Numerical studies of flow over a circular cylinder at Re=3 900［J］.Physics of Fluids，2000，12（2）：403-417.

［9］Lei C，Cheng L，Kavanagh K.A finite difference solution of the shearflow overa circularcylinder［J］. Ocean Engineering，2000，27：271-290.

［10］Lilly D K.A proposed modification of the Germano subgridscale closure model［J］.Physics of Fluids，1992，4（4）：633-635.

［11］ Ong L，Wallace J.The velocity field of the turbulent very near wake of a circular cylinder［J］.Exp.Fluids，1996，20：441-453.

［12］Sumner D，Akosile O O.On uniform planar shear flow around a circular cylinder at subcritical Reynolds number［J］.Journal of Fluids and Structures，2003，18：441-454.

［13］ Zang Y，Street R L，Koseff J R.A non-staggered grid，fractional step method for time-dependent incompressible Navier-Stokes equationsin curvilinearcoordinates［J］.Journal of Computational Physics，1994，114：18-33.

［14］Tamura H，Kiya M，Arie M.Numerical study of viscous shear flow past a circular cylinder［J］.Transactions of the Japan Society for Mechanical Engineering，1994，46（404）：555-564.

［15］ Tamura T，Kitagishi T.Application of the interpolation method in generalized coordinate system to wake flows around a circular cylinder［J］.J.Struct.Constr.Eng.，AIJ，2001，545：27-34.

［16］ Williamson C H K.Vortex dynamics in the cylinder wake［J］.Annu.Rev.Fluid Mech，1996，28：477-539.

［17］ Zhang H Q，Fey U，Noack B R.On the transition of the cylinder wake［J］.Phys.Fluids，1995，7（4）：779-794.

［18］趙 楊，曹曙陽，Tamura Y，等.雷暴沖擊風模擬及其的風洞試驗研究［J］.振動與沖擊，2009，28（4）：1-3.

［19］瞿偉廉，王錦文.下擊暴流的風荷載模擬［J］.武漢理工大學學報，2008，30（2）：70-74.