考慮受壓屈曲的圓鋼管桿單元等效彈塑性滯回模型

謝道清，沈 金，鄧 華，張 瑞

(1.浙江大學 空間結構研究中心，杭州 310058;2.浙江大學 建筑設計研究院，杭州 310027)

網架、網殼等網格結構的彈塑性地震響應分析受到越來越多的重視，主要有兩個方面的原因。首先，作為應用最廣的一類大跨度結構形式，網格結構被普遍認為有相當好的抗震性能。然而近些年的震害情況表明［1］，網格結構發生各種程度破壞的情況并不少見，而定量分析這些震害發生的原因(包括設計的不合理性)就不能回避彈塑性分析的問題。其次，對于按非地震作用或僅考慮小震作用來設計桿件截面的網格結構，在中震或大震條件下會呈現怎樣的動力響應特點以及破壞形態，這也必須進行彈塑性分析。

關于網格結構彈塑性地震響應方面的研究總體上還比較薄弱，這也導致了我國相關抗震設計規范對網格結構在中震和大震下的抗震措施基本上缺乏詳細規定。此外在具體進行彈塑性分析時，目前的文獻中桿單元普遍采用的是理想彈塑性本構模型(圖2)，即拉壓極限狀態均為軸向屈服［2-4］。然而在中震、大震等強震作用下，網格結構中桿件在受壓狀態下顯然發生的是屈曲破壞，因此理想彈塑性模型并不能客觀地反映壓桿的實際工作性態。正是出于對此基本問題的考慮，本文將對網格結構中常用規格的圓鋼管桿件進行不同長細比條件下的非線性屈曲分析，重點考察這些桿單元的受壓極限承載力、平衡路徑以及屈曲后卸載路徑，并繪制拉壓往復作用下桿件軸力P和兩端節點相對位移Δ的滯回曲線。進一步統計這些不同規格鋼管桿單元的滯回曲線控制點與桿件長細比λ之間的關系，將P-Δ曲線轉換成統一描述的應力-應變(σε)曲線，以此提出一個能夠同時考慮受拉屈服和受壓屈曲的圓鋼管桿單元的等效彈塑性滯回模型。文中以一個球面網殼作為算例，應用該等效彈塑性滯回模型進行了網殼在罕遇地震作用下的彈塑性時程響應計算。通過與理想彈塑性模型計算結果的比較，分析了桿件應力應變反應和結構薄弱區域分布上的差異，以此來考察本文提出的等效彈塑性滯回模型的有效性。

1 桿件有限元分析

1.1 考察的鋼管規格

根據網格結構常用鋼管規格，選擇表1所列的46根不同截面和長度的圓鋼管桿件作為考察拉壓滯回規律的樣本桿件。鋼管材質為Q235鋼，屈服強度fy=235 MPa，彈性模量E=2.06e5 MPa，泊松比為 0.3。表1中樣本桿件的長細比范圍在40～180之間。

表1 樣本桿件的長細比λ及其對應的截面和長度Tab.1 Slenderness ratios of steel circular-tube specimens and their corresponding cross sections and lengths

1.2 有限元模型

鋼管桿件的計算簡圖如圖1所示，兩端鉸接，受軸向荷載P作用。采用LS-DYNA軟件建立鋼管桿件的有限元模型，管壁采用Shell163殼單元模擬。殼單元分別沿截面周圈和桿長方向按16和80等分劃分，單元總數共計1 280個。殼單元采用理想彈塑性本構模型(圖2)，符合Von Mises屈服準則。受壓屈曲分析時計入桿件初彎曲的影響［5］，初彎曲形狀按該殼單元有限元模型的一階特征值屈曲模態引入，最大撓度取v0=L/1 000［6］。

1.3 桿件加載和卸載

使用LS-DYNA軟件進行加卸載計算。加卸載按位移控制，速度為10-3m/s。首先計算桿件受壓屈曲前后的平衡路徑，并獲得受壓臨界荷載Pcr。受壓屈曲后的最大加載位移為8Δcr，其中Δcr為Pcr對應的桿端相對位移。然后再考察桿件在屈曲后平衡路徑上2Δcr、4Δcr、8Δcr位移點處的卸載情況，跟蹤卸載路徑直至受拉屈服。最后再從受拉屈服段反向卸載并重新加壓至桿件屈曲，以得到完整的拉壓P-Δ滯回曲線。

1.4 拉壓滯回特點

在46根樣本桿件中選擇三根典型長細比桿件來闡述圓鋼管桿單元的加載和卸載滯回曲線特點。三根桿件的規格分別為:Ф180×8(L=2.5 m，λ =41)、Ф140×4.5(L=5.0 m ，λ =104)和 Ф75.5 ×3.75(L=4.5 m，λ=177)。圖3給出了三根桿件在不同加、卸載情況下的P/Py-Δ/Δcr曲線，其中Py=-Afy，A為桿件截面積。為方便對比，故圖3中的縱橫坐標均用相對值來表達，如橫坐標Δcr/Δ=1對應的縱坐標值為Pcr/Py。

圖1 鋼管桿件的計算模型Fig.1 The computational model of circular-tube members

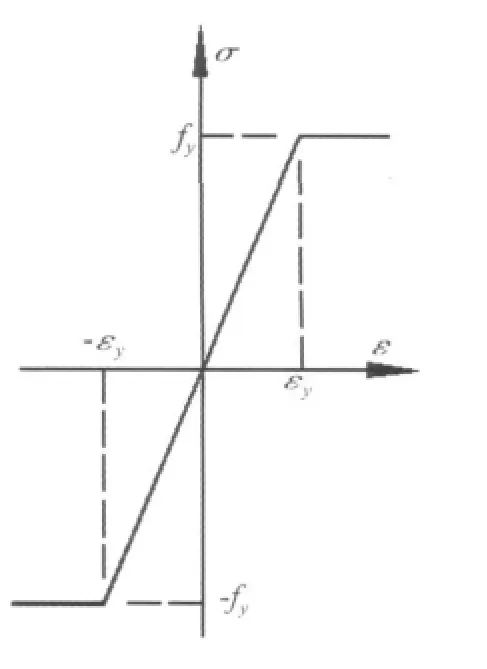
圖2 理想彈塑性模型Fig.2 The ideal elasto-plastic model

(1)單向受壓加載

圖3(a)為三根桿件僅在壓力加載下的P/Py-Δ/Δcr曲線。可以看出，小長細比(λ=41)桿件的屈曲臨界荷載與極限屈服荷載之比(Pcr/Py)高達0.988 7，到達臨界點前基本呈線彈性反應，但屈服后承載力較快下降。對于中等長細比(λ=104)桿件，Pcr/Py下降至0.641 6，屈曲前還基本呈線彈性反應，屈曲后承載力也較快下降，但后段的下降速度相對趨緩。對于λ高達177的桿件，Pcr/Py下降到0.278 6，屈曲前后曲線過渡平緩，臨界點并不明顯，且屈曲后路徑下降平緩。

(2)2Δcr處卸載

圖3 三根典型桿件在加卸載作用下的P/Py-Δ/Δcr曲線Fig.3 The P/Py-Δ/Δcrcurves of three circular-tube specimens under loading and unloading

在三根桿件受壓屈曲后變形至2Δcr時，進行卸載并拉至屈服，然后再反向卸載和加壓以形成一個拉壓循環，其P/Py-Δ/Δcr滯回曲線如圖3(b)所示。可以看出，屈曲后路徑上的卸載曲線并不像理想彈塑性模型那樣呈直線變化。對于小長細比(λ=41)桿件，卸載初期基本還按直線卸載，曲線斜率接近彈性加載斜率，但是在受拉狀態后期至屈服前，曲線斜率快速減小。而大長細比(λ=177)桿件的卸載特點卻相反，卸載曲線前期斜率小，在進入受拉區后斜率增大并總體呈線彈性變化。對于中等長細比(λ=104)桿件，卸載曲線在到達受拉屈服前斜率雖有所變化，但幅度很小。

當卸載至受拉屈服后，再反向卸載，此時受拉區的P/Py-Δ/Δcr曲線基本上和理想彈塑性模型一樣呈線性變化。繼續反向卸載進入受壓狀態時，屈曲前后曲線形狀也基本和初始的加壓曲線相同，無非是由于受拉屈服使得曲線沿橫坐標向左平移了一個相對伸長值。

(3)4Δcr和 8Δcr處卸載

圖3(c)和(d)分別為三根桿件在受壓屈曲后路徑上的4Δcr和8Δcr位移點進行卸載，并反向加載的P/Py-Δ/Δcr滯回曲線圖。總體上看，滯回曲線的變化規律和2Δcr處卸載的滯回曲線相差不大。小長細比桿件卸載曲線在受壓區斜率較大，在受拉區后期斜率變小。而大長細比桿件在卸載初期曲線斜率較小，進入受拉區后斜率增大。中等長細比桿件的卸載曲線斜率總體變化依然相對較小。此外，8Δcr位移點的卸載曲線斜率相對4Δcr位移點的卸載曲線變化平緩些。當桿件由受拉屈服段反向卸載至受壓屈曲時，P/Py-Δ/Δcr曲線變化規律和2Δcr處卸載的滯回曲線基本一致。

2 等效彈塑性滯回模型

2.1 基本思路

從圖3中可以看出，考慮受壓屈曲的圓管桿單元P-Δ滯回曲線與理想彈塑性模型的主要不同之處是受壓區的臨界點、屈曲后路徑以及屈曲后的卸載路徑，而且以上三方面內容與桿件長細比λ密切相關。而在受拉區，P-Δ曲線是基本符合理想彈塑性模型的。因此為便于計算機處理，可采用如圖4所示(以拉為正、壓為負)的分段線性化辦法來描述受壓屈曲后路徑和卸載路徑。首先，將桿件屈曲后路徑用 Δcr、2Δcr、4Δcr、8Δcr對應的坐標點來分段模擬，即圖4中的3～6點。其次，考慮到不同長細比桿件屈曲后卸載曲線的斜率變化情況，將 2Δcr、4Δcr和 8Δcr處的卸載曲線按兩個直線段來模擬，即通過增加如圖4所示的7～9三個過渡點來定義。如果屈曲后的卸載點在3～6點之間，可相應在2、7～9點間按等比例線性插值來確定該卸載曲線的過渡點，并最終定義其卸載路徑。至此，考慮受壓屈曲的圓鋼管桿單元滯回模型實際上就可通過圖4中的1～9號點來描述。

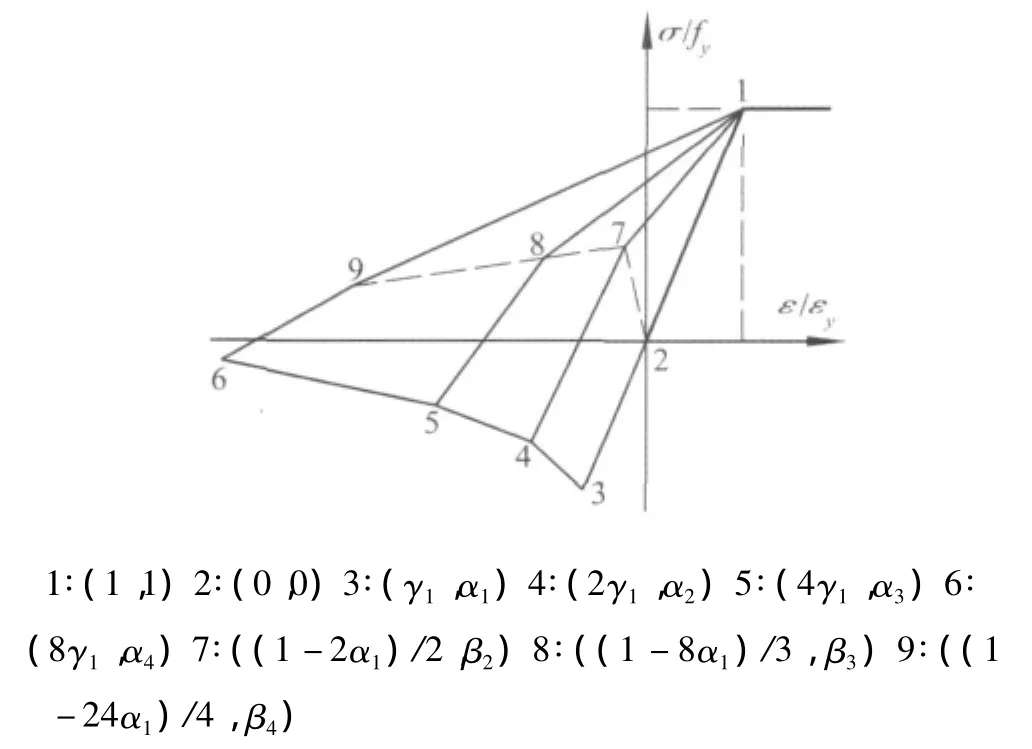
圖4 等效彈塑性滯回模型Fig.4 The equivalent elasto-plastic hysteretic model

進一步將表1所列46根樣本桿件的P-Δ曲線按圖4形狀進行無量綱歸一化處理，即縱坐標表示桿件的名義應力σ=(P/A)和fy的比值，橫坐標表示桿件的名義應變ε=(Δ/L)和εy的比值，其中εy=fy/E。通過歸一化，易知九個控制點中，點1和點2的坐標分別為(1，1)、(0，0)。設臨界點 3 的坐標為(γ1，α1)，則點4 ～6的坐標可表示為(2γ1，α2)、(4γ1，α3)和(8γ1，α4)。根據對46根桿件的歸一化滯回曲線分析，確定卸載路徑上7～9過渡點的相對應變值取(1-2α1)/2、(1-8α1)/3、(1-24α1)/4比較恰當，而此三點的相對應力值分別定義為 β2、β3、β4，如圖 4。

2.2 控制參數的擬合

在圖4定義的圓鋼管桿單元等效彈塑性滯回模型中，有八個控制參數需要確定，即 γ1、α1、α2、α3、α4、β2、β3、β4。于是在46根樣本桿件的歸一化滯回曲線上，確定該八個控制參數并統計其與長細比λ的關系，見圖5(a)～(h)所示。可以看出，有些控制參數和長細比λ的關系為單調遞減，而有些為先遞減再遞增，因此統一采用簡單的多項式形式進行擬合，并發現三次曲線就能達到較好的擬合精度。于是，進一步可得出以上八個參數和長細比λ∈［40，180］的近似關系為:

圖5 八個控制參數和長細比λ的關系Fig.5 The relationships between 8 governing parameters and slenderness ratios λ

2.3 等效彈塑性模型的校驗

用表1所列樣本桿件以外的多根圓鋼管桿件來考察等效彈塑性滯回模型的有效性。首先采用殼單元有限元法計算出這些桿件的拉壓滯回曲線，然后將計算結果和等效彈塑性滯回模型的擬合結果進行比較。結果表明，等效彈塑性模型的計算結果和有限元法的計算結果非常吻合，特別在控制點處。考慮到篇幅限制，本文僅給出了一根校驗桿件Ф127×4.5(L=3.25 m，λ=75)的計算結果，見圖6。

其次，臨界點控制參數α1實際上與我國《鋼結構設計規范》(GB50017-2003)中的壓桿穩定系數φ有非常相近的含義，盡管后者是根據邊緣屈服準則確定的。由于本文桿件的初始缺陷僅考慮了初彎曲，接近GB50017-2003規定的A類截面［7］，故將 α1和A類截面的穩定系數φ進行比較，如圖7。可以發現，α1和φ在長細比λ∈［40，180］區域的誤差在5%之內，吻合很好。

3 罕遇地震作用下的球面網殼計算

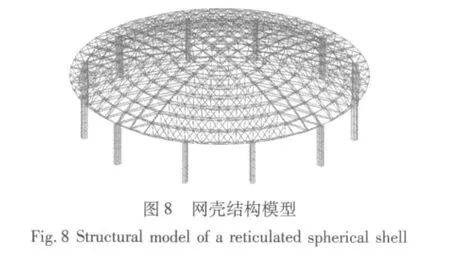
3.1 網殼模型

圖8所示為一個Kiewitt型雙層球面網殼屋蓋。網殼跨度為60 m，矢高6 m，厚度2 m。屋蓋均勻支承在周邊12根10 m高的C30混凝土柱上，柱截面為1.2 m×0.8 m。網殼承受的荷載標準值為:靜荷載 0.5 kN/m2(不包括結構自重);活荷載為1.0 kN/m2;溫度差為±20℃;風荷載0.5 kN/m2。考慮以上非地震荷載的工況組合，采用Mstcad軟件對該網殼進行滿應力設計以確定桿件的截面，其中滿應力設計時所選擇的鋼管截面規格如表1。

3.2 地震波

參照我國《建筑抗震設計規范》(GB50011-2001)，對結構進行8度罕遇地震下的彈塑性時程分析。地震加速度時程采用Big-bear波［8］，按三向輸入(X為主方向，如圖9)。截取了該波的前38 s記錄(共1 900個點)，X向加速度最大值按8度罕遇地震取400 cm/s2，三向加速度峰值的比例調整系數為1∶0.85∶0.65，結構阻尼比取0.035。在輸入Big-bear波之前的2 s內，先以漸增豎向加速度的方式施加重力荷載代表值(1.0靜+0.5活)，然后再疊加上Big-bear波的加速度時程，以此同時考慮結構的重力荷載代表值和地震動的作用。

3.3 結構響應計算

采用Ansys軟件進行結構在Big-bear波作用下的彈塑性時程計算。網殼桿件考慮兩種材料模型:模型一為圖2所示的理想彈塑性模型;模型二為圖4所示的考慮壓桿屈曲的等效彈塑性模型。在采用模型二計算時，利用Ansys軟件的APDL語言控制計算流程，即不斷記錄每一個荷載步所求得的桿件變形量，然后通過重啟動(restart)命令并利用前一荷載步的桿件變形量來修改材料本構模型，以此實現等效彈塑性模型加、卸載迭代求解。

(1)失效桿件分布和薄弱區域分析

從理想彈塑性模型的計算結果發現，在罕遇地震作用下網殼桿件始終處于線彈性階段，即最大拉壓應力絕對值均沒有超過屈服應力fy。而等效彈塑性模型的計算結果中，有110根桿件出現了受壓屈曲，并最終存在殘余塑性應變(指名義應變Δ/L)。發生受壓屈曲的桿件主要分布在由外至內的2～4環的上下弦層內，尤其是下弦層以及部分支座附近(如圖9)，其中最大名義塑性應變(總名義應變扣除彈性應變)為-1.015×103με。進一步考察這些桿件的非地震作用控制內力，發現其中大多數桿件位于殼體邊緣彎矩效應和薄膜內力效應相互抵消的區域，桿件(特別是弦桿)軸力較小，因此在滿應力設計時其截面配置主要由長細比控制，截面普遍較小。

(2)桿件的應力和應變

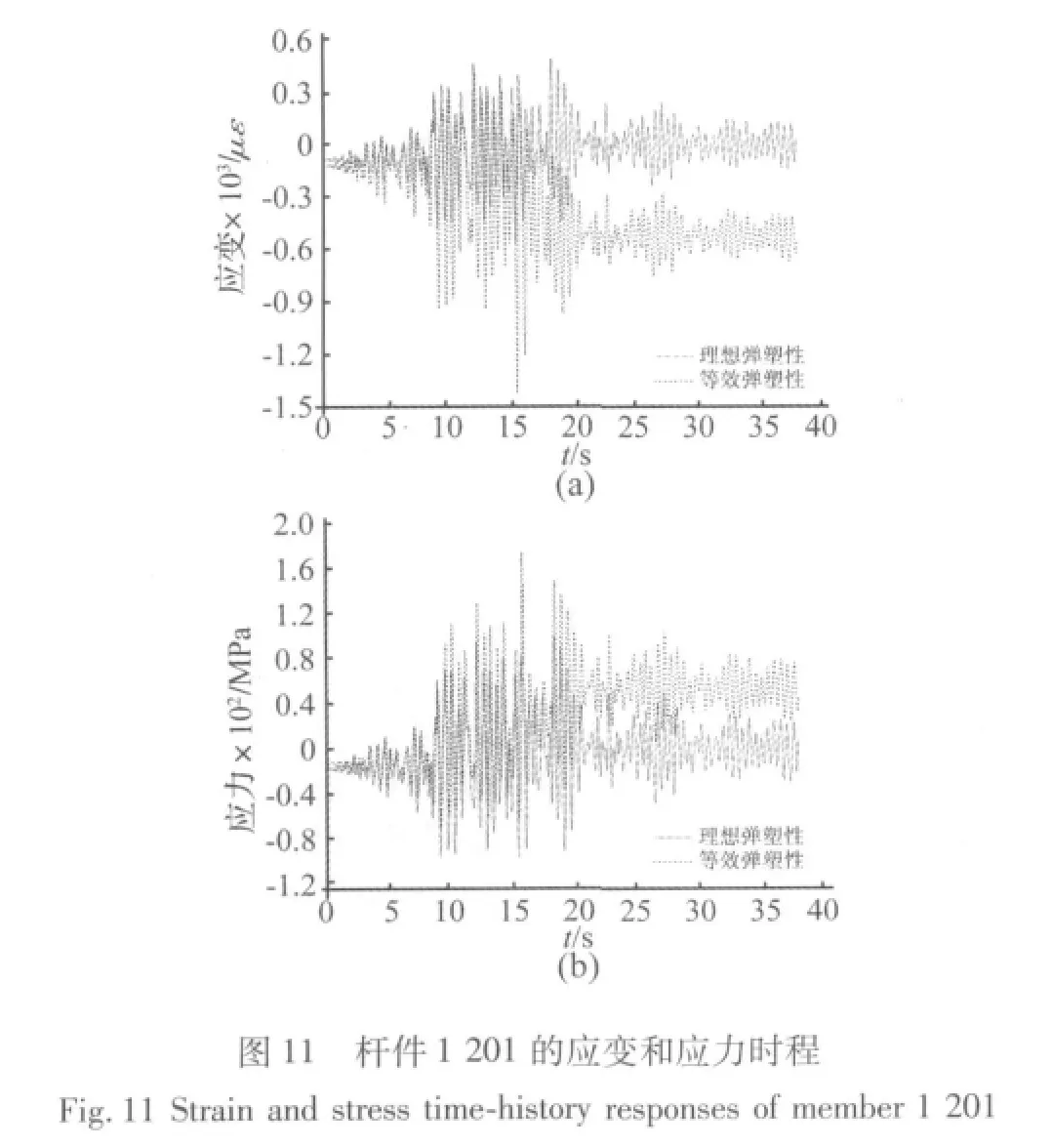
圖10和11分別給出了名義塑性應變最大的兩根桿件1 191、1 201(如圖9)的應力、應變時程曲線。可以看出，采用等效彈塑性模型所求得的桿件名義壓應變要大于理想彈塑性模型的計算結果，兩者最大值相差2倍以上。而采用等效彈塑性模型所求得的名義壓應力要小于理想彈塑性模型的結果。究其原因，主要是因為等效彈塑性模型中當桿件發生受壓屈曲后，其承載力和軸向剛度將大大低于不考慮屈曲的理想彈塑性模型。此外，理想彈塑性模型中構件的時程響應始終處于彈性狀態，而等效彈塑性模型的結果是構件最終存在明顯的殘余應變和應力。

4 結論

要研究網格結構對應于中震、大震設防水準的抗震措施，就不能回避對結構進行動力彈塑性性能分析。而現代數值計算技術的快速發展，為網格結構動力彈塑性響應的精細化分析提供了有力支持。本文的目的就是試圖將強震作用下網格結構中桿件受壓屈曲這一基本問題盡可能細致考慮，以克服理想彈塑性模型高估了桿件受壓承載力的缺點。較為有利的是，無論是受拉屈服還是受壓屈曲，桿單元實際上僅需通過桿件軸力和伸長量這兩個簡單參數來定義其受力狀態，因此形式上就可以將屈服和屈曲問題進行統一描述，而且是在構件層面上。此外，計算分析也發現盡管考察的桿件規格不同，但它們的受壓屈曲路徑和屈曲后卸載路徑從大的趨勢上看是相同的，P-Δ曲線的控制參數也主要跟長細比相關，這也為建立能同時考慮受拉屈服和受壓屈曲的圓鋼管桿單元等效彈塑性滯回模型提供了條件。

本文提出的等效彈塑性滯回模型與理想彈塑性模型的差別主要反映在桿件受壓時的加、卸載曲線上，特別是屈曲后的卸載路徑隨桿件長細比不同存在一些差異，即小長細比桿件的初期卸載剛度(曲線斜率)大而后期小，而大長細比桿件正好相反，因此在等效彈塑性模型中引入了八個控制參數來加以描述，形式上略顯復雜。但是，由于這八個參數僅與長細比相關，在實際計算(包括插值計算)時并不復雜，用較短的程序段就可以實現。更為重要的是，只要在常規的結構彈塑性分析中對材料的本構模型進行修改就能將桿件屈曲問題加以考慮，總體上應該是方便的。此外，與理想彈塑性模型相比，本文算例結果表明了采用等效彈塑性滯回模型確實能夠有效地反映網格結構在地震作用下的受壓屈曲桿件分布情況，并有助于分析結構的薄弱區域。

［1］中國建筑科學研究院編.2008年汶川地震建筑震害圖片集［M］.北京:中國建筑工業出版社，2008.

［2］范 峰.空間網殼結構彈塑性地震響應及抗震性能分析［J］.哈爾濱建筑大學學報，1999，32(1):132-37.

［3］薛素鐸，王建寧，曹 資，等.鋼網殼彈塑性地震反應分析［J］.北京工業大學學報，2001，27(1):50-53.

［4］沈世釗，支旭東.球面網殼結構在強震下的失效機理［J］.土木工程學報，2005，38(1):11-20.

［5］ Kala Z. Sensitivity assessmentofsteelmembersunder compression［J］.Engineering Structures，2009，31:1344-1348.

［6］陳 驥.鋼結構穩定-理論與設計［M］.北京:科學出版社，2001.

［7］夏志斌，姚 諫.鋼結構——原理與設計［M］.北京:中國建筑工業出版社，2010.

［8］ PEER Strongmotion database［EB OL］. http://peer.berkeley.edu/products/strong_ground_motion_db.html.