計及陀螺效應的翼吊式機翼-發動機系統結構動力學特性研究
周健斌,章俊杰,孟 光
(1.中國商用飛機有限責任公司 上海飛機設計研究院,上海 200232;2.上海交通大學 機械系統與振動國家重點實驗室,上海 200240)
現代大型客機設計廣泛采用機翼下吊發動機的布局形式。隨著飛機設計技術的發展,現代大型客機朝著加大機翼展弦比、采用輕質材料、減小結構剛度、采用高涵道比大推力發動機的方向發展,因此翼下吊發動機不僅影響飛機的氣動力布局,發動機轉子產生的陀螺效應對飛機結構動力學特性以及氣動彈性特性的影響也日益突出。王彬文[1]等用有限元方法研究了轉子陀螺效應對帶有翼吊發動機系統振動特性的影響,結果表明陀螺效應對其固有特性的影響是不可忽略的。
具有陀螺效應的彈性體問題可歸結為陀螺彈性系統問題。Eleuterio[2-6]和 Hughes[7]首次提出了陀螺彈性系統問題并針對自旋航天器研究了一類具有分布陀螺力矩的彈性系統的動力學特性。Peck等[8,9]在此基礎上提出了運用嵌入在結構中的角動量來實現結構自適應調諧,如頻移、模態耦合和解耦、相位調整等。針對一類帶有旋轉部件的機械臂,Yamanaka[10-11]分析了端部帶有轉子的均質梁的動力學和穩定性問題,其轉子轉軸沿梁的軸向。Li等[12]研究了端部帶有任意方向旋轉軸的轉子的柔性連接的穩定性問題。
本文從陀螺彈性系統理論出發,以帶有橫向轉子的Bernoulli-Euler懸臂梁為研究對象,運用Hamilton變分原理建立了計及發動機陀螺效應的機翼彎扭耦合動力學模型,分析了系統的動力學特性,研究了發動機陀螺效應對系統固有特性的影響。
1 陀螺效應的耦合作用
如圖1所示,轉子垂直于梁展向安裝,設轉子自轉角速度為Ω,極慣性矩為Jp,則轉子對其質心的動量矩為:

當梁發生y方向(面內)的彎曲振動以及扭轉振動時,轉子轉動方向將隨梁振動而發生改變,此時轉子做繞y方向的橢圓進動。根據轉子動力學理論,該橢圓進動由正進動和反進動合成。設轉子繞y方向的進動角速度為ω,則轉子產生陀螺力矩:

其方向垂直于Ω與ω組成的平面。設Ω與ω夾角為φ(φ?1),則陀螺力矩大小可表示為:

該力矩與φ成正比,相當于彈性力矩。在正進動情況下(如圖1),陀螺力矩作用使得梁的剛度提高;反之,在反進動情況下,梁的剛度減小。由此,陀螺力矩使得梁的面內彎曲模態和扭轉模態發生耦合,并影響系統的剛度。

圖1 陀螺力矩耦合作用示意圖(正進動)Fig.1 Illustration of the mechanism of the gyroscopic coupling effect
2 動力學模型
為研究發動機陀螺效應對機翼動力學特性的影響,將機翼-發動機系統簡化為一端固支的彎扭耦合Bernoulli-Euler懸臂梁結構,忽略發動機與機翼間的連接剛度,如圖2(a)所示。機翼翼展為l,半弦長為b,右手坐標系o-xyz原點o位于機翼根部,ox軸與機翼剛軸重合,oy軸沿飛機航向。發動機重心位置為(xs,ys,zs),機翼重心軸在-y方向的距離為e。圖2(b)所示為變形后x=xs處機翼弦向截面示意圖。o'為機翼剛軸與截面交點,截面位移為v、w,截面繞o'轉角為 θ。Cw為截面重心,發動機重心位置Cs,發動機重量為ms,轉子轉速為Ω,轉動矢量方向與剛軸垂直。

圖2 機翼-發動機系統示意圖Fig.2 Illustration of the wing-engine system
由Hamilton變分原理

可推導得系統動力學方程,其中 δU、δTw、δTs和 δW分別為機翼勢能、機翼動能、發動機動能和非保守外力做功的變分。由彎扭耦合懸臂梁動力學分析,機翼勢能的變分為:
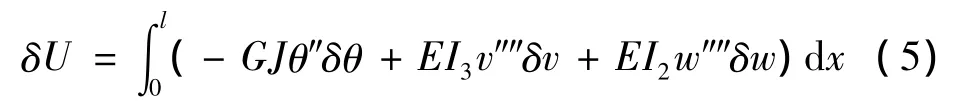
其中,EI2為梁的面外彎曲剛度,EI3為梁的面內彎曲剛度,GJ為梁的扭轉剛度。
機翼動能的變分可表示為:
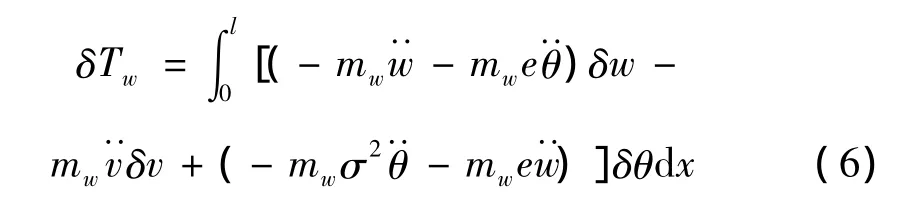
其中,mw為機翼單位長度質量,e為機翼截面重心與剛軸的距離(重心在剛軸前為正),σ為機翼單位長度截面繞剛軸的慣性半徑。
對發動機動能分析可知,發動機的動能的變分由兩部分組成,δTs=δTm+δTr,其中 δTm為發動機集總質量的動能的變分,δTr為發動機轉子的轉動動能的變分。

由轉子動力學理論,當機翼變形時,向量Ω的偏轉角在oxy和oyz平面的投影分別為v'和θ,由此,發動機轉子的轉動的動能可表示為:

其中,Jp為轉子繞其轉軸的極轉動慣量,Jd為轉子的赤道轉動慣量。對Tr求變分可得:

將式(5)~(7)和(9)代入式(4)可得如下計及發動機陀螺效應的系統動力學方程:


式中,δD()為 Dirac函數。“'”表示對X求導,“·”表示對τ求導。
3 動力學特性分析
采用extended Galerkin[13]方法對系統動力學方程進行離散化,令:

選取如下滿足邊界條件的函數作為基函數:

代入方程(13)~方程(15),積分可得離散后的系統方程:
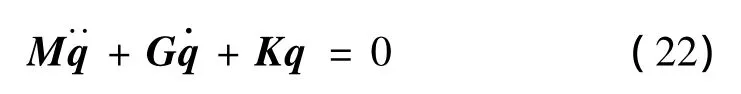
為驗證系統模型,選取 Goland[14]機翼模型參數EI2=9.76 ×106N·m2,EI3=9.76 ×106N·m2,GJ=9.88 ×105N·m2,mw=35.75 kg/m,σ =0.49 m,e=0.18 m,l=6.10 m,計算發動機位于機翼根部且 Ω=0 rad/s時系統前五階固有頻率,結果如表1所示。根據梁的動力學特點,取N1=5、N2=5、N3=3。通過對比可知,本文計算結果與文獻相吻合,數學模型及計算方法具有較高的精度。

表1 Goland梁前五階固有頻率Tab.1 Modal frequency of the first 5 modes for the Goland wing
3.1 轉速對系統固有特性的影響


表2 轉子結構參數Tab.2 Structural parameters of the engine rotor
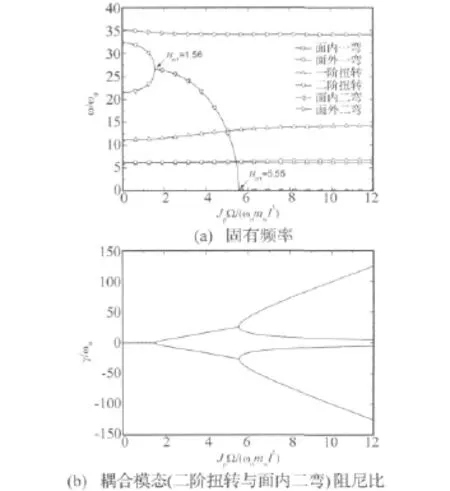
圖3 Goland機翼固有頻率和阻尼比隨發動機無量綱慣性矩變化曲線Fig.3 Modal frequency and damping ratio vs.nondimensional rotor moment of inertia of the Goland wing
由圖3可知,隨著發動機轉子慣性矩的增大,在發動機陀螺力矩作用下,當系統二階扭轉模態與面內二階彎曲模態相鄰時,該兩階模態相互耦合,系統二階扭轉模態頻率增大、面內二階彎曲模態頻率減小,即在陀螺力矩作用下,系統二階扭轉模態剛度增大,而二階彎曲剛度減小;此時系統特征值為純虛數,各階振型有固定節線,即發動機陀螺力矩影響系統的剛度。當轉子慣性矩增大至=1.56時,上述耦合模態對應的特征值為共軛復數重根,模態頻率重合,模態阻尼分岔并出現負阻尼,系統處于動態失穩狀態;如圖4所示為=2.52時系統前六階振型,此時系統第四階模態與第五階模態相互耦合,具有相同的振型曲線,且振型無固定的節線。重合后該模態頻率隨著發動機轉速的增大而加速降低=5.55時,該耦合模態出現過阻尼,模態頻率為零,相應模態阻尼進一步分岔。

圖4 H=2.52時系統前六階振型圖Fig.4 Mode shapes of the first 6 modes with=2.52
3.2 臨界轉速
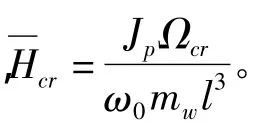
以上如圖5所示為臨界無量綱慣性矩及=0時系統模態頻率ω/ω0隨機翼剛軸與重心軸距離e/l的變化曲線。由圖可知=0時系統面外彎曲模態及扭轉模態的頻率隨著e/l的增大而變化,當其中某一階頻率曲線接近并與面內彎曲模態頻率曲線相交時,將相交點臨近區域稱為頻率相交影響區域,如圖5中陰影區域Ⅰ和Ⅱ所示。在頻率相交影響區域內,隨著發動機轉子轉速的提高,發動機陀螺效應使得頻率相交模態參與耦合,系統動態失穩,此時系統臨界轉速快速降低,且在頻率相交點臨界頻率達到最小值,如圖6所示為e/l=0.01時,系統模態頻率隨發動機轉子轉速變化Campbell圖,從圖中可以看出,由于系統結構參數使得系統面內一階彎曲頻率和面外一階頻率耦合,在陀螺效應的作用下,系統第一、二階頻率在=0.02 時即出現共軛特征值,導致動態失穩。在非頻率相交影響區域內,系統臨界阻尼不隨e/l變化。


如圖7所示為臨界無量綱慣性矩及=0時系統模態頻率ω/ω0隨機翼慣性半徑σ/l的變化曲線。與前述情況類似,由于慣性半徑的變化系統在0≤≤0.15范圍內出現頻率相交影響區域Ⅰ、Ⅱ、Ⅲ和Ⅳ,在這些區域內系統臨界轉速快速下降,而在頻率相交影響區域內,系統臨界轉速隨慣性半徑的增大而增大。

圖7 Goland機翼臨界無量綱慣性矩隨變化曲線Fig.7 Critical nondimensional rotor moment of inertia vs. σ of the Goland wing
4 結論
本文運用Hamilton原理建立了計及發動機陀螺效應的機翼動力學數學模型,通過系統特性分析、研究得到如下結論:
(1)受發動機陀螺力矩的耦合作用,隨著發動機陀螺慣性矩的增大,機翼面內彎曲模態頻率增大,扭轉模態頻率降低,且模態振型相耦合。
(2)當面內彎曲模態與扭轉模態相鄰時,且發動機陀螺無量綱慣性矩大于臨界穩定值時,系統特征值出現共軛復重根,參與耦合的模態頻率重合,系統動態失穩。
(3)在非頻率相交影響區域內,系統動態臨界穩定無量綱慣性矩隨機翼慣性半徑σ的增大而增大,而剛軸與重心軸的距離e對無影響。
[1]王彬文,孫俠生,齊丕騫.轉子陀螺效應對系統振動特性的影響[J].振動工程學報,2010,23(增刊):63-67.
[2] D'Eleuterio G M T.On the theory of gyroelasticity[J].Journal of Applied Mechanics,Transactions ASME,1988,55(2):488-489.
[3]D'Eleuterio G M T,Hughes P C.Dynamics of gyroelastic spacecraft[J].Journal of Guidance,Control,and Dynamics,1987,10(4):401-405.
[4]D'Eleuterio G M T,Hughes P C. General motion of gyroelastic vehicles in terms of constrained modes[C].1985,384-390.
[5] D'Eleuterio G M T,Hughes P C.Dynamics of gyroelastic continua[J].Journal of Applied Mechanics,Transactions ASME,1984,51(2):415-422.
[6] D'Eleuterio G M T.Dynamics of gyroelastic vehicles[R].UTIAS Report(University of Toronto,Institute for Aerospace Studies),1986.
[7]Hughes P C,D'Eleuterio G M T.Modal parameter analysis of gyroelastic continua[J].Journal of Applied Mechanics,1986,53(4):918-924.
[8]Peck M A,Cavender A R.Structural tuning through embedded angular momentum[C].44th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,2003,2:1462-1469.
[9]Peck M A,Cavender A R.Practicable gyroelastic technology[C].27th Annual AAS Rocky Mountain Guidance and Control Conference,2004,118:239-253.
[10]Yamanaka K,Heppler G R,Huseyin K.On the dynamics and stability of a beam with a tip rotor[C].the 35th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics,and Materials Conference,1994,2:1031-1038.
[11] Yamanaka K, Heppler G R, Huseyin K. Stability of gyroelastic beams[J].AIAA Journal,1996,34(6):1270-1278.
[12] Li L,Heppler G R,Huseyin K.Stability of a flexible link with an arbitrarily oriented tip rotor and a conservative tip load[C].2000,2:1472-1477.
[13] Fletcher C.Computational Galerkin methods[M].Springer-Verlag New York,1984.
[14] Goland M.The flutter of a uniform cantilever wing[J].Journal of Applied Mechanics,1945,12(4):197-208.
[15] Banerjee J,Su H.Dynamic stiffness formulation for beams undergoing free transverse and lateral vibration with torsional coupling[C].44th AIAA/ASME/ASCE/AHS Structures,Structural Dynamics,and Materials Conference,2003.

