考慮玻璃剛度的高層幕墻地震響應數(shù)值分析

楊顏志，金先龍，2，王 建，李 燁

(1.上海交通大學 機械與動力工程學院，上海 200240;2.上海交通大學 機械系統(tǒng)與振動國家重點實驗室，上海 200240;3.華東建筑設計研究院有限公司，上海 200002)

玻璃幕墻作為一種新型建筑結構，由于具有其它結構無法比擬的優(yōu)點已被廣泛地應用于建筑物的外部裝飾［1-2］。然而玻璃幕墻本身的結構特點，給工程設計尤其是災害條件下的極限設計帶來了一定的挑戰(zhàn)。

一般認為玻璃幕墻結構的力學性能主要由幕墻支承結構決定，玻璃本身對幕墻影響不大，因此在相關研究中往往忽略玻璃因素，或者將玻璃等效為質量施加于幕墻支承結構［3］。然而對于超高層懸掛式幕墻結構，由于幕墻整體面積大結構復雜，當承受較大風載和地震作用時，幕墻支承結構將產(chǎn)生較大變形，此時是否需要考慮玻璃剛度對幕墻整體的貢獻就值得探討了。國內外目前對于玻璃參與工作后對幕墻結構力學性能的影響研究不多。文獻［4-6］僅討論了考慮玻璃剛度對于幕墻結構靜力與基礎振動特性的影響，對于幕墻設計較為關鍵的地震荷載，未發(fā)現(xiàn)考慮玻璃剛度的幕墻地震響應研究。

本文針對上述問題，依托上海某在建超高層大廈，建立了包含大廈主體結構、幕墻支承結構和幕墻玻璃結構的三維精細有限元模型，并計算了三者相互作用情況下的地震響應。計算在上海超級計算中心“魔方”超級計算機上利用顯式并行計算軟件LS-dyna完成。同時為分析玻璃參與工作后對幕墻結構的影響，將考慮玻璃剛度模型的幕墻地震響應結果與未考慮玻璃剛度模型的結果進行了對比分析，其中未考慮玻璃剛度模型將玻璃等效為質量施加于幕墻支承結構。

1 顯式有限元方法

某一時刻變形體的運動方程可表示為:

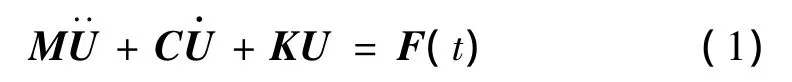
采用顯式中心差分方法［7-8］求解運動方程(1)，在已知0，…，tn時間步解的情況下，求解tn+1時間步的解，運動方程為:

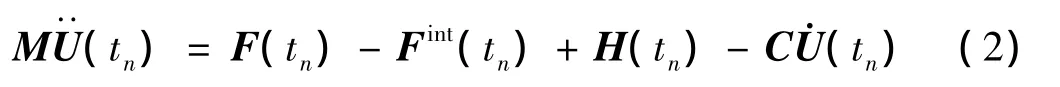
式中:F(tn)為外力向量列陣，F(xiàn)int(tn)為內力矢量，H(tn)為沙漏阻力。可求得時刻tn的加速度:

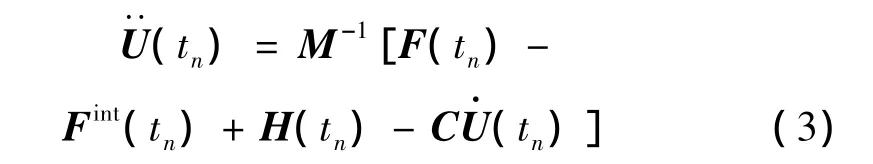
tn+1時刻的速度和位移由下面公式求得:

式(1)中的阻尼矩陣C常采用Rayleigh阻尼模型:

其中，ω1、ω2分別為系統(tǒng)的一階、二階陣型的頻率;ξ為系統(tǒng)的阻尼比。

由于采用集中質量矩陣，運動方程的求解是非耦合的，無須組集總體剛度矩陣，并且采用中心單點積分，因此顯式有限元方法大大節(jié)省了存儲空間和求解機時。

2 工程實例

2.1 工程簡介

上海某在建超高層建筑位于浦東新區(qū)陸家嘴中心位置。整個大廈高632 m，共126層，最高樓層高度582.5 m，高寬比達到7。大廈由主體結構和外部懸掛式幕墻結構組成，沿豎向分為8個區(qū)域和塔冠部分。在每個區(qū)域均布置有設備層，將主體結構和外部幕墻分為9個幕墻區(qū)域。

大廈幕墻通過大廈主體的參考中心，從建筑底部逐層扭轉縮小直到頂部，每層扭轉約1°左右，總扭轉角約120°;每層縮小比例約0.5%，總縮小比例約52.8%，從而使大廈形成獨特的扭轉外型。由于其幕墻結構的特殊性，幕墻抗震設計成為關注的重點。圖1為大廈結構剖面圖。

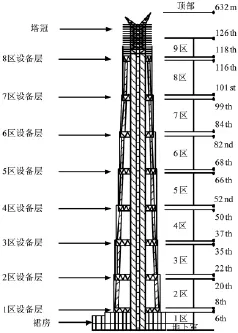
圖1 大廈結構剖面圖Fig.1 Structure profile of the building

2.2 三維有限元模型

根據(jù)大廈設計資料，采用三維建模方法建立全尺寸大廈三維有限元模型，包括大廈主體結構模型，幕墻支承結構模型和幕墻玻璃結構模型。模型采用實體單元模擬巨型柱，用殼單元模擬核心筒、樓板與玻璃，用三維梁單元模擬桁架結構和幕墻支承結構。對于附加恒載和活載，將其換算為相應質量，并用等效質量單元模擬。如圖2為大廈整體三維有限元模型。

圖2 大廈整體三維有限元模型Fig.2 Global 3-D finite element model of the building

大廈有限元模型真實還原了建筑的“巨型框架-核心筒-伸臂桁架”結構體系。按照真實尺寸建立了8根巨型柱模型和4根角柱模型，同時建立了全尺寸的核心筒模型，巨型柱和核心筒之間通過環(huán)帶桁架模型、伸臂桁架模型和徑向桁架模型連接，從而構成主體結構模型。圖3為大廈局部三維有限元模型，給出了大廈模型體系的構成。

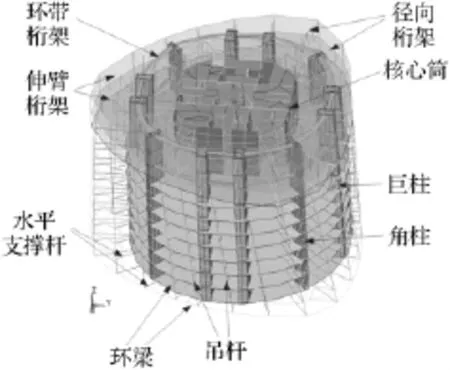
圖3 大廈三維局部有限元模型Fig.3 Local 3-D finite element model of the building

大廈外部幕墻采用懸掛式結構體系，有限元模型真實還原了建筑幕墻的結構。圖4為幕墻結構有限元模型。其中圖4(a)為幕墻結構精細有限元模型，圖4(b)為幕墻結構局部放大后的精細有限元模型。從圖中可知，幕墻玻璃固定于周邊曲梁上，通過豎向吊桿懸掛于本區(qū)的設備層樓板。大廈樓層沿徑向布置有多根水平支撐桿，連接周邊曲梁和樓板，從而為幕墻結構提供水平向支撐，水平支撐桿與周邊曲梁采用固連連接，與樓板采用鉸接連接。懸掛式幕墻重力荷載通過布置于設備層的徑向桁架傳遞給環(huán)帶桁架，然后將荷載傳遞至巨型柱與核心筒。相鄰玻璃模型間布置了龍骨模型。由于幕墻結構隨樓層逐漸扭轉收縮，因此造成相鄰兩層間幕墻玻璃的交錯，為還原真實構造特點連接相鄰兩層幕墻玻璃模型，在相鄰兩層幕墻玻璃間建立了連接曲梁模型。

大廈主體結構，如巨柱、剪力墻等均由不同強度等級的混凝土構成，所使用的混凝土等級有C50、C60和C70。巨型鋼桁架和幕墻支承結構為不同截面形狀的結構鋼，其型號為Q235、Q345和Q390。玻璃龍骨為鋁合金材料，玻璃為剛化玻璃。由于本文主要研究小震彈性狀況下幕墻結構的地震響應，此時大廈主體結構和幕墻結構均處于彈性狀態(tài)，因此主要材料均采用線彈性模型模擬，表1列出了主要混凝土材料的計算參數(shù)，表2列出了主要金屬材料的計算參數(shù)。玻璃材料密度為2 560 kg/m3，彈性模量為 7.2E+10Pa，泊松比為 0.2。

建筑整體三維有限元模型單元數(shù)511 392，節(jié)點數(shù)602 716。其中實體單元數(shù)9 592，殼單元數(shù)316 610，梁桿單元數(shù)167 621，質量單元數(shù)17 569，模型總重量約72.6 萬噸。

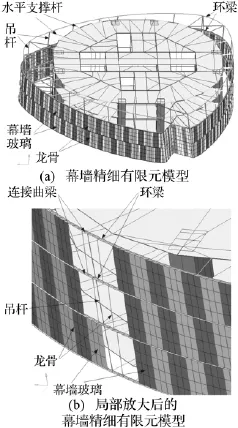
圖4 幕墻結構有限元模型Fig.4 Curtain wall finite model of the building

表1 混凝土材料參數(shù)Tab.1 Mechanic parameters of concretes

表2 金屬材料參數(shù)Tab.2 Mechanic parameters of metals

3 數(shù)值計算結果與分析

3.1 數(shù)值計算概況

選取模型結構響應較大的1985年墨西哥地震波(MEX波)作為輸入地震波，采樣時間間隔為0.02 s，并按照50年超越概率63%的常遇地震烈度對其進行調幅處理。為考慮三向地震波交互作用下的地震響應，地震波三向同時輸入，其中X向:Y向:Z向(豎向)按1∶0.85∶0.65的峰值關系進行整體調幅，主向加速度調幅峰值為0.035 g。圖5為調幅后MEX地震波的加速度時程，總計算時間為30s。對于高層鋼筋混凝土結構，結構阻尼比依據(jù)規(guī)程［9］取5%。本次計算在上海超級計算中心“魔方”超級計算機上利用顯式計算軟件LS-dyna完成，計算采用區(qū)域分解的并行算法，實際使用了32個CPU。

圖5 MEX地震波調幅后加速度時程Fig.5 Time history of scaled MEX wave

3.2 結構動力特性

對大廈結構的動力特性進行了計算分析，并將考慮玻璃剛度大廈模態(tài)與未考慮玻璃剛度大廈模態(tài)進行對比，其中未考慮玻璃剛度模型將玻璃等效為質量施加于幕墻支承結構。圖6為考慮玻璃剛度大廈前6階振型，其中1、4階振型為X向平動，2、5階振型為Y向平動，3、6階振型為Z向(豎向)扭轉。

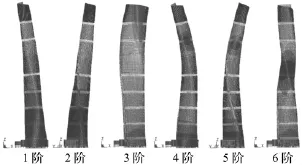
圖6 大廈模型前6階振型Fig.6 The first six vibration mode of the building

表3中列出了考慮玻璃剛度大廈前6階自振周期，并與未考慮玻璃剛度大廈對比。從表中可知，大廈低階模態(tài)反映了主體結構固有特性，外部幕墻跟隨主體結構運動。兩組計算結果偏差小于5%，可認為是否考慮玻璃剛度對大廈主體無明顯影響。

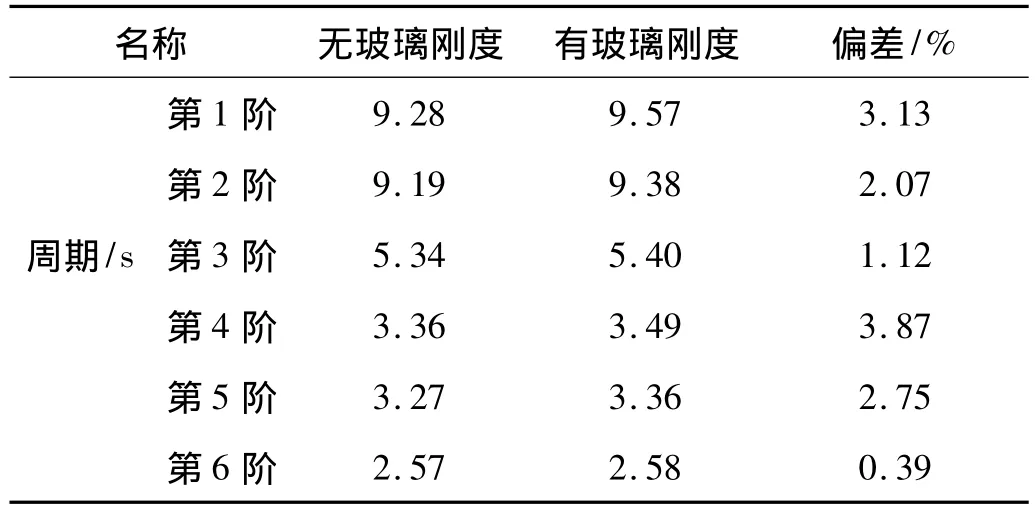
表3 大廈前6階自振周期對比Tab.3 The first six vibration period of the building

3.3 幕墻結構加速度響應分析

本次計算以X向地震波為主向，重點分析了X向相關地震響應。加速度指標是幕墻結構設計的重要因素之一，本文重點分析了小震工況下幕墻結構的加速度分布。并將考慮玻璃剛度幕墻加速度響應與未考慮玻璃剛度幕墻加速度響應進行對比。

圖7分別給出了考慮玻璃剛度模型和未考慮玻璃剛度模型大廈頂層(126層)幕墻結構X向最大加速度時程，即最大加速度節(jié)點的加速度時程。可知無玻璃剛度模型頂層的加速度響應大于有玻璃剛度模型。

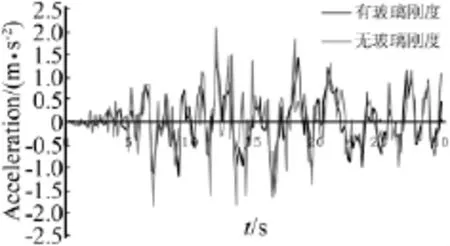
圖7 頂層幕墻結構X向最大加速度時程Fig.7 Time history of the maximal X-direction acceleration at top story

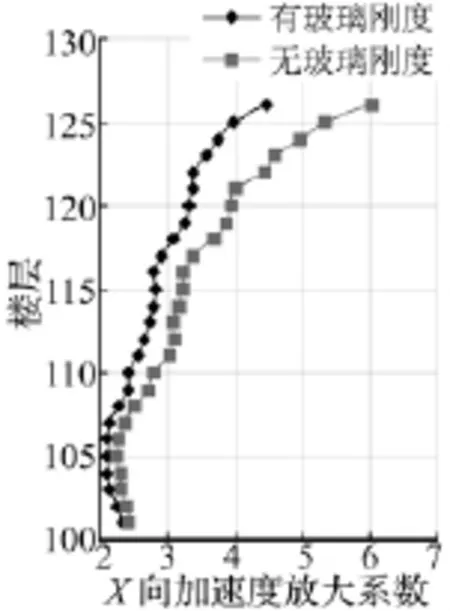
圖8 幕墻結構X向加速度放大系數(shù)分布Fig.8 X-direction acceleration magnification of curtain wall

對于高層建筑結構，往往在建筑頂部位置會出現(xiàn)較大的動力放大效應，因此本文重點分析了8區(qū)和塔冠部分幕墻結構的加速度放大系數(shù)，圖8分別給出了考慮玻璃剛度模型和未考慮玻璃剛度模型幕墻結構X向加速度放大系數(shù)隨樓層的分布。可知從101層開始兩組計算結果偏差逐漸增大，在頂層126層位置考慮玻璃剛度模型X向加速度放大系數(shù)為4.48，未考慮玻璃剛度模型最大加速度放大系數(shù)為6.03，偏差達到25.6%。可認為玻璃在高樓層加速度放大系數(shù)較大區(qū)域對加速度響應抑制作用明顯，此結論與文獻［6］的研究成果有一定相似性。

3.4 幕墻結構變形響應分析

地震作用下幕墻結構的變形也是設計中需要考慮的重要因素。如圖9所示，大廈單塊幕墻玻璃與樓層高度相等，本文主要分析單層幕墻模型頂部節(jié)點與底部節(jié)點間X向相對變形，例如節(jié)點a和b間的變形，c和d之間的變形，相對變形與樓層高度的比值就是幕墻的層間位移角，單層幕墻不同節(jié)點處層間位移角最大值即為該層最大層間位移角。

圖10分別給出了8區(qū)幕墻和5區(qū)幕墻X向最大層間位移角隨樓層分布，并將考慮玻璃剛度大廈模型與未考慮玻璃剛度大廈模型最大層間位移角對比。可知考慮玻璃剛度后幕墻最大層間位移角偏小5%～10%，這是由于玻璃本身剛度限制了幕墻結構形變。因此忽略玻璃剛度可能導致幕墻形變計算值偏大，使設計結果偏保守。此外隨著樓層增高，最大層間位移角逐漸增大，無玻璃結構模型8區(qū)幕墻X向最大層間位移角為1/555，出現(xiàn)在第110層;5區(qū)幕墻X向最大層間位移角為1/674，出現(xiàn)在第62層。不同分區(qū)X向最大層間位移角符合規(guī)范［10］和相關文獻［11］研究的限值(1/500)。

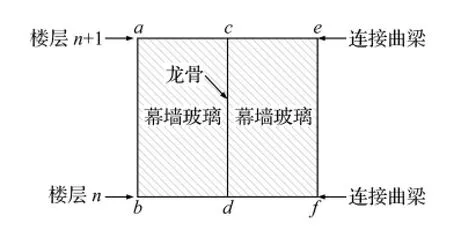
圖9 幕墻結構相對變形測量節(jié)點Fig.9 Measuring nodes of relative deformation in curtain wall

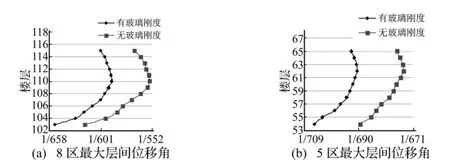
圖10 不同幕墻分區(qū)X向最大層間位移角Fig.10 X-direction maximal inter-story drift ratio of different sub-zone curtain wall

3.5 幕墻支承結構應力分析

幕墻支承結構由不同鋼梁組成，包括吊桿、環(huán)梁和水平支撐桿。本文重點選取8區(qū)幕墻中變形響應較大的第110層作為關鍵分析對象，并將考慮玻璃剛度幕墻支承結構應力與未考慮玻璃剛度進行對比。圖11給出了單層幕墻支承結構平面內關鍵位置的編號，幕墻結構在關鍵位置2、4和6處設置有三根限位桿。

圖12分別給出了110層幕墻支承結構關鍵位置處吊桿、環(huán)梁和水平支撐桿的應力，并對比兩組模型的結果。可知由于無玻璃剛度模型幕墻變形相對較大，因此造成其對應的桿件應力相對偏大，對應桿件應力增大為15% ～25%。關鍵位置1、3和5處吊桿應力較大，應力較大吊桿出現(xiàn)在幕墻曲率較大位置。由于分區(qū)幕墻局部結構低階模態(tài)振型均為曲率較大位置的豎向振動，因此主要豎向受力構件吊桿在此處應力偏大。關鍵位置2、4和6處環(huán)梁和水平支撐桿應力較大，由于限位桿的存在造成局部的應力集中，導致附近桿件應力偏大。主要桿件在小震作用下應力均小于50 MPa，符合抗震性能要求。

圖11 單層幕墻支承結構關鍵位置編號Fig.11 Number of key position in single story of curtain wall supporting structure

圖12 110層幕墻結構關鍵位置桿件應力Fig.12 Stress of beam in key positions for 110th story

4 結論

(1)考慮玻璃剛度模型與未考慮玻璃剛度模型大廈低階模態(tài)吻合較好，說明是否考慮玻璃剛度對大廈主體結構影響較小。

(2)考慮玻璃剛度后幕墻最大層間位移角比未考慮玻璃剛度偏小5%～10%，說明玻璃剛度增大了幕墻整體剛度，對于幕墻結構的抗震設計是有利的。忽略其影響可能導致設計結果偏保守。

(3)較高樓層位置，兩組模型加速度放大系數(shù)隨著樓層的增高偏差逐漸增大，在頂層126層位置考慮玻璃剛度模型加速度放大系數(shù)較未考慮玻璃剛度模型偏小25.6%，說明玻璃在高樓層加速度放大系數(shù)較大區(qū)域對加速度響應抑制明顯。

(4)考慮玻璃剛度后幕墻主要桿件應力比未考慮玻璃剛度偏小15%～25%。應力較大吊桿出現(xiàn)在幕墻曲率較大位置，應力較大環(huán)梁和水平支撐桿出現(xiàn)在限位桿附近。最終計算結果均滿足抗震設防要求，可作為該工程幕墻抗震設計參考依據(jù)。

［1］ Behr R A，Asce P E F.Design of architectural glazing to resist earthquakes［J］.Journal of Architecture Engineering，2006，12(3):122-128.

［2］石永久，李 勇，王元清.點支式幕墻單層索網(wǎng)諧波地震響應的幾何非線性研究［J］.振動與沖擊，2009，28(10):31-35.

［3］李 勇，石永久，王元清.單層索網(wǎng)玻璃幕墻與主體結構地震響應的整體分析［J］.建筑科學，2009，25(7):5-10.

［4］馮若強，武 岳，沈世釗.單索幕墻體系中的玻璃與索協(xié)同工作機理研究［J］.西安建筑科技大學學報，2006，38(5):619-623.

［5］馮若強，武 岳，沈世釗.考慮玻璃參與工作的單層平面索網(wǎng)幕墻結構靜力性能研究［J］.建筑結構學報，2005，26(4):99-106.

［6］馮若強，花定興，武 岳.單層平面索網(wǎng)幕墻結構玻璃與索網(wǎng)協(xié)同工作的動力性能研究［J］.土木工程學報，2007，40(10):27-33.

［7］金先龍，李淵印.結構動力學并行計算方法及應用［M］.北京:國防工業(yè)出版社，2008.

［8］丁峻宏，金先龍，郭毅之.沉管隧道地震響應的三維非線性數(shù)值模擬方法及應［J］.振動與沖擊，2005，24(5):18-22.

［9］JGJ3—2003高層建筑鋼筋混凝土結構技術規(guī)程［S］.北京:中國建筑工業(yè)出版社，2002.

［10］JGJ102—2003玻璃幕墻工程技術規(guī)范［S］.北京:中國建筑工業(yè)出版社，2003.

［11］黃寶鋒，盧文勝，曹文清.建筑幕墻抗震性能指標探討［J］.土木工程學報，2009，42(9):8-12.