人均用電量法在區域飽和負荷預測中的應用研究

王 偉，房婷婷

（東南大學 電氣工程學院，南京 210096）

改革開放30多年來，我國工業化和城市化水平不斷提高，各大區和省級電網的負荷水平也節節攀升，負荷峰谷差不斷拉大，電網面臨的擴建任務艱巨而緊迫[1]。

過去為了給電網擴容的順利進行提供有價值的參考，規劃和建設部門普遍會預先組織開展一系列針對性的中長期負荷預測工作。近年來學術界提出了飽和負荷的概念和不少有別于中長期負荷預測的新的飽和負荷預測方法[2—3]，但相關預測工作的重視程度和推廣應用仍相對偏弱。

飽和負荷概念的提出確有其必然性和實效性。受土地面積、環境資源、規劃定位等多方面因素的制約，一個國家（地區、城市）的經濟總量不可能無限制的增長，負荷水平當然也一樣。用電量和經濟發展水平之間是相輔相成的關系，二者的增長趨勢也基本相同，都可以用飽和增長S形曲線（通常可以通過logistic曲線擬合）來加以描述。從圖1中可以很直觀的看出相關變量的變化趨勢，最終趨于有限值，即達到飽和。

基于上述背景，給出人均用電量法預測飽和負荷的數學模型及其主要參數的確定方法，并通過一個實例驗證了該模型的預測精度。

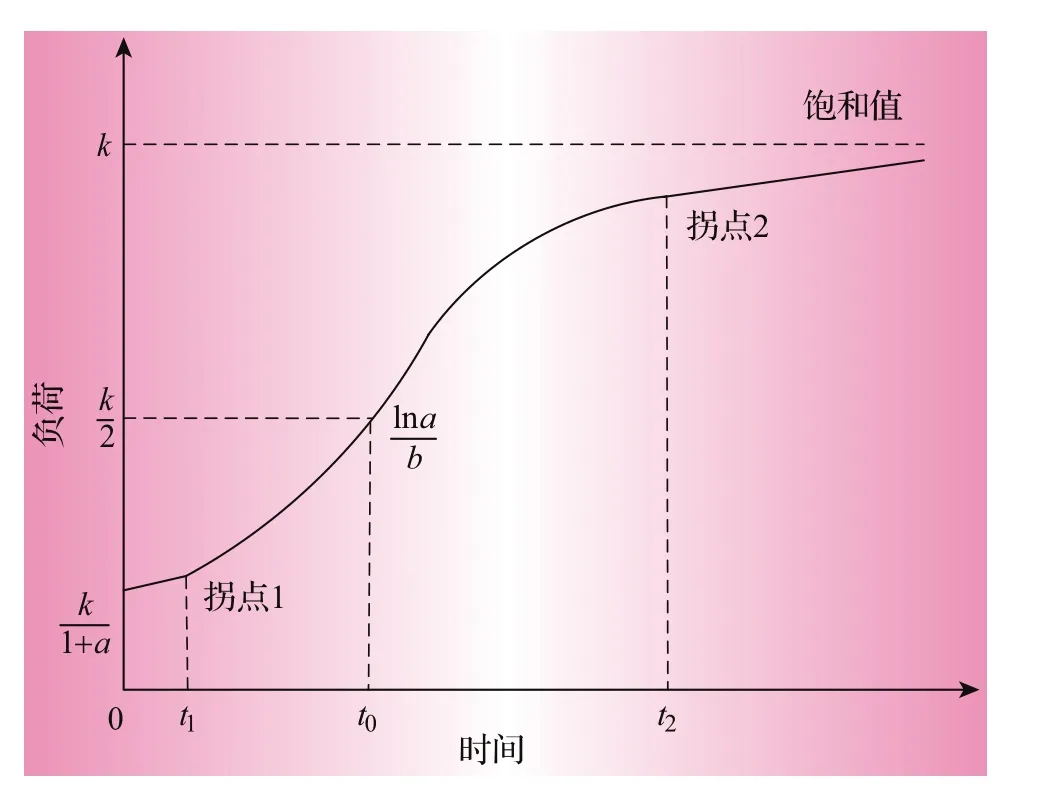
圖1 飽和增長S型曲線（logistic曲線）

1 預測思路

基于人均用電量方法預測飽和負荷的初步思路是：從宏觀預測的角度出發，以某地區的人均用電量We和該地區人口總量Nt的歷史統計數據為基礎，從中分析挖掘We和Nt的增長規律，建立各自的預測子模型，預測出二者未來若干年各自的增長趨勢，然后根據一定的飽和判定條件判定出人口達到飽和的年份并取該年的人口總量與預測出的飽和人均用電量值相乘，即得該地區的全社會飽和用電總量，進而根據式（1）求出飽和負荷的預測值。

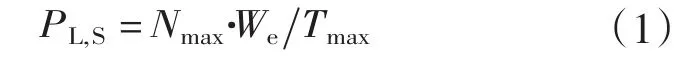
式中：PL，S表示飽和負荷；Nmax表示飽和人口；Tmax表示最大負荷利用小時數。如果能分別對上式中的3個量We、Nmax、Tmax的變化趨勢做出較為精確的預測，則PL，S的預測值也有望獲得較高的預測精度。

2 飽和人口的預測

如今，許多發達國家和地區的人口早已進入了增速緩慢甚至是負增長的階段，我國自計劃生育國策實施以來，人口的自然增長率呈現出逐年下降的趨勢，特別是部分沿海經濟發達省份，低生育率帶來的社會人口老齡化問題已十分突出。可以預見的是，受資源環境、土地面積等硬性條件的天然限制，一個地區的人口總量不可能無限制的增長，最終人口的自然增長率會無限趨近于0，人口總量將達到一個完全飽和的極限值并在其附近擺動。

針對人口總量增長趨勢的預測，選擇采用飽和增長趨勢預測中的一種較為成熟的模型——修正指數曲線[4—5]來建模預測。修正指數曲線適用于對一類特殊增長現象的描述，即初期增長相對迅速，隨后增長率逐漸趨緩，最終以k為增長極限。其模型表達式如式（2）所示

式中：k＞0；a＜0；0＜b＜1。

模型參數的確定采用“三和法”進行估算。所謂“三和法”就是把觀測值區間等分為3段，每段含有n個數據，對各段數據求和，分別記為S1、S2、S3，然后解含有3個未知數的方程組，各參數的表達式如式（3）—式（5）所示

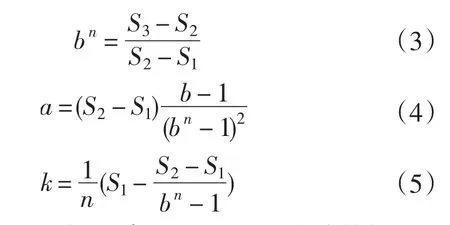
以1980—2009年福建省人口歷史統計數據[6]為例，代入式（3）—式（5）計算，可以算得修正指數模型各參數的估計值為：a=-1 942.354 7，b=0.969 9，k=4 444.436 9。

圖2為1980—2009年福建省人口總量和預測人口總量的增長趨勢。從圖中可以看出，依據該模型對1980—2009年的福建省人口做出的預測誤差很小，絕大多數年份的絕對百分誤差小于1%，與實際值的擬合度好，可信度高。

西方現代人口理論一般認為，人口自然增長率降至2‰以下時，該區域人口就基本達到了飽和狀態。篇幅所限，僅給出2010—2050年部分年份的福建省人口預測值（每5年為一個單位），如表1所示。按照自然增長率2‰的判斷標準，福建省人口總量達到飽和的年份應為2045年，預測的飽和人口為4 178萬人左右。上述飽和人口只是在理想條件下的預估值，還需要在未來根據實際情況的變動做出及時的、必要的修正。

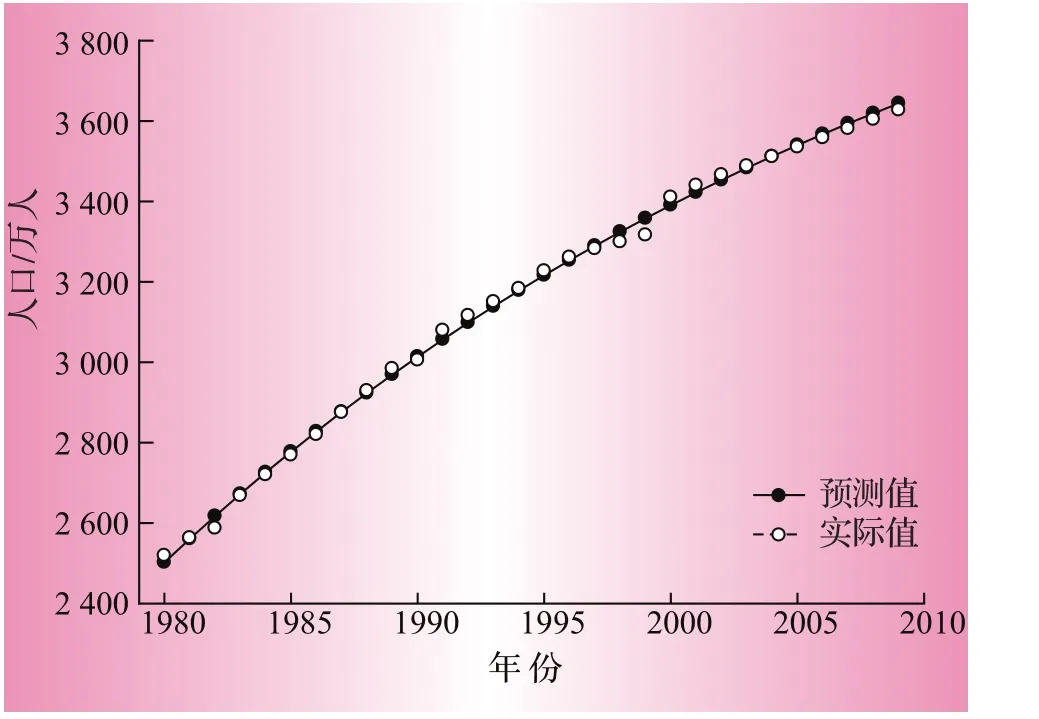
圖2 1980—2009年福建省人口增長實際值與預測值的比較

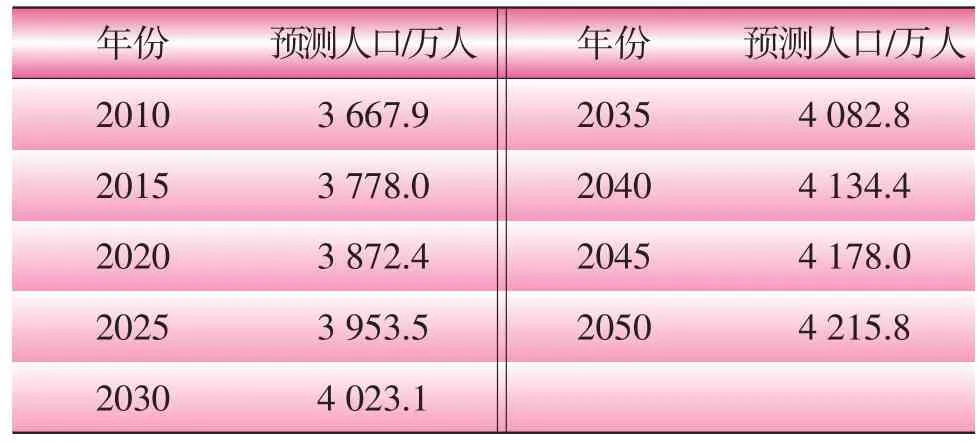
表1 2010—2050年福建省人口預測值

3 飽和人均用電量的預測

選用線性擬合建模法預測飽和人均用電量。借助MATLAB軟件的CETOOL工具箱，以歷史統計數據為依據擬合S型曲線方程，獲取到方程所需的參數，然后通過該模型方程進一步推算出未來飽和人均用電量的值。

上文提到的logistic曲線可以應用于此。logistic曲線是一類內線性模型，或稱作可化為線性模型的回歸問題。變形后的logistic曲線可化為線性函數

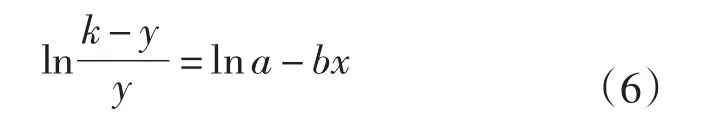
式中：x為年份；y為人均用電量。

仍然以福建省為例，將1980—2009年福建省人均用電量數據[6]輸入工具箱，使用線性擬合功能，很容易就能得到式（6）中所需的參數值a=e218,b=-0.108,k=11 000。該工具箱給出的擬合曲線和實際曲線的相關系數為0.985，表示擬合效果良好。曲線的最大值為k=11 000，即借助MATLAB的CETOOL工具箱預測出福建省的飽和人均用電量為11 000 kWh/人。

一個國家或地區的人均用電量水平可以在很大程度上反映出其當前的經濟實力。對比發達國家諸如日本[7]、韓國[8]近些年的人均用電量數據（東亞一帶的消費習慣和社會結構相似，具有較高的可借鑒性）不難發現，我國的人均用電量水平雖比之過去已有較大幅度的提升[9]，但總體上還是相對落后的。一旦區域經濟達到真正意義上的相對飽和以后，各發達經濟體最終人均用電量數據的差異性應該不會太大。

4 飽和負荷預測

由于不同行業之間的最大負荷利用小時數差別明顯，產業結構的不斷調整和需求側管理手段之間的相互作用，以及負荷特性的實時變動等因素給直接預測Tmax的變化趨勢帶來不小的阻力，因此采用文獻［10］中提出的基于概率論與數理統計知識的預測方法，以全社會總用電量的預測結果為自變量，來建模預測相應年份的最大負荷值。可以認為，當全社會總用電量達到飽和時所對應的年最大負荷即為該區域的飽和負荷預測值。導出的預測模型方程

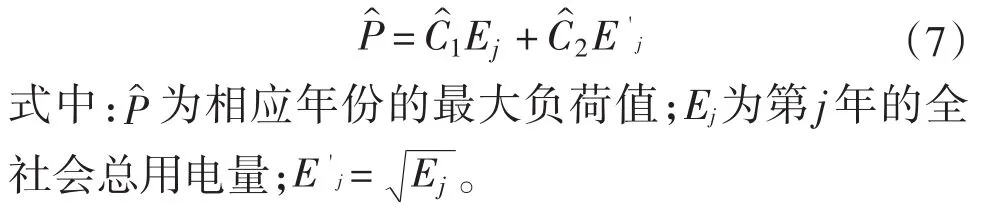
將福建省2000—2009年的用電量和最大負荷歷史統計數據[6]代入，可以算出預測模型方程的參數C=［17.954 1，-47.489 9］T，代入式（7）即可得福建省電力系統最大負荷預測的模型。

按照公式（7）計算，可以求得2000—2009年的福建省最大負荷的預測值，并結合實際值給出相應的預測誤差，如表2所示。從表2中的預測誤差來看，大部分年份的誤差都在1%～3%左右，與實際值非常接近，模型的預測效果良好。

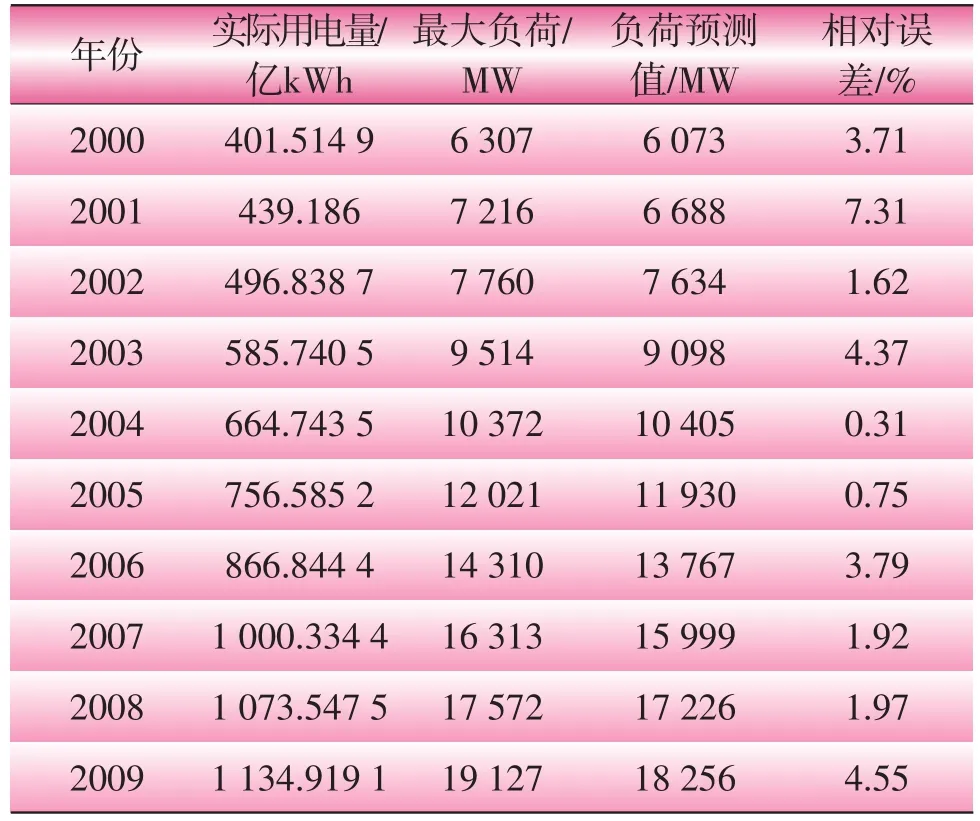
表2 福建省全社會用電量和最大負荷

式（1）中的3個量現已分別完成直接或間接性的預測，結合式（7），即可求出最終的飽和負荷預測值。對于福建省而言，取2045年的預測人口4 178萬人，飽和人均用電量11 000 kWh/人，二者相乘得出最終福建省全社會飽和用電總量，約4 595.8億kWh。代入式（9）中算得福建省的飽和負荷約為7 718.45萬kW。

5 結束語

本文介紹了人均用電量方法在飽和負荷預測中的應用，該方法的優勢劣勢都十分明顯。它的最大優勢在于清晰直觀、原理簡單易懂。它的缺點也十分明顯，例如：①模型參數是根據固定的歷史統計數據來確定的，因而很難根據未來的情況變化做出及時的調整；②模型的使用過程相對死板，難以靈活的利用專家經驗和意見；③未能將影響負荷的多方面因素都系統的考慮進去。

鑒于上述問題的存在，想要達到更高的預測精度，就必須采用新的、更為合理的預測方法。隨著人工智能、系統動力學等模型精度更高的預測方法逐漸被學術界開發出來并開始獲得實際應用，飽和負荷預測領域的研究之路必將越走越寬。

［1］ 楊又華，張銀芽.問診華中電力緊張新局勢[J].國家電網，2010（7）：51-53.

［2］ 江新琴，李喜蘭.基于空間飽和負荷密度的城市遠景飽和負荷預測[J].福州大學學報：自然科學版，2008,36(4)：532-536.

［3］ 何永秀，吳良器，戴愛英，等.基于系統動力學與計量經濟模型的城市飽和負荷綜合預測方法[J].電力需求側管理，2010,13(1)：21-25.

［4］ 王吉全.修正指數曲線在電力負荷預測中的應用[J].計算機工程，2006,32(18)：253-254.

［5］ Alexander Horch,Alf J Isaksson.A modified index for control performance assessment[J].Journal of Process Control,1999,9(6)：475-483.

［6］ 林文芳.崛起的海峽西岸經濟區——新中國60年的福建[M].北京：中國統計出版社,2009.

［7］ 張干周.日本電力工業概況(I)[J].國際電力，2003(5)：4-9.

［8］ 劉育新.韓國電力工業現狀以及電力體制改革[J].華北電業，2002(1)：44-46.

［9］ 朱成章.中國未來十五年電力需求試測[J].節能，2006（5）：3-5.

[10］ 傅文峰.年電量作為自變量預測年最大負荷[J].華中電力,1993,6(3)：58-59,71.

（本欄責任編輯陳 穎 劉嘉婧）