附參數的條件平差與按行獨立的加權總體最小二乘法估計的一致性研究

周擁軍，朱建軍，鄧才華

1.上海交通大學船舶海洋與建筑工程學院，上海200240；2.中南大學地球科學與信息物理學院，湖南長沙410083

1 引 言

經典測量平差方法是假設觀測誤差服從正態分布，以觀測值的加權最小二乘條件為目標函數，以觀測值與參數之間的函數模型線性化為約束條件，并根據約束條件的不同形式得到各種平差模型。文獻［1］于20世紀80年代提出了統一的平差模型——附限制條件的條件平差法，經典攝影測量平差理論均以此模型為基礎。由于附限制條件的條件平差問題解算較復雜，目前諸多測量平差軟件和理論大多以間接平差模型為基礎，現代測量平差與數據處理理論仍然是以高斯－馬爾可夫模型為核心，通過該模型在不同層面上的擴充、發展形成的若干新理論、新方法［2－3］。近年來雖然出現了一些擴展模型，但應用上仍相對較少［4－6］。近年來，國內外許多學者采用總體最小二乘（total least squares，TLS）估計方法解算諸如曲線擬合、坐標變換等問題［7－10］。TLS法是文獻［11］于1980年提出的對線性變量含誤差（errors－invariables，EIV）模型的參數估計方法，該方法考慮了系數矩陣的誤差，是一種不同于經典測量平差原理的新方法。文獻［12］從理論上證明：對于Y≈Dθ（Y、D分別表示含誤差的系數矩陣，θ表示待估計參數）的線性EIV模型，當增廣系數矩陣［D Y］的所有元素均服從獨立等精度分布時，TLS方法與經典最小二乘的估計結果一致。但這種假設在實際應用中往往不成立，因此需要采用加權總體最小二乘方法（weighted total least squares，WTLS）。由于實際問題中系數矩陣元素間的方差關系極為繁雜且難以準確求定，文獻［13］根據系數矩陣權的結構將加權總體最小二乘問題簡化為：廣義TLS方法、按元素獨立（element－wise）的WTLS方法、按列獨立（columnwise）的WTLS方法、按行獨立（row－wise）的WTLS方法等，在已有的應用中往往采用簡化權結構或等價權［14－16］方法解決具體問題。而許多包含不等精度觀測值的EIV模型如曲線擬合、坐標變換、直接線性變換等可近似假定條件方程間獨立或分塊獨立，從而簡化為RWTLS問題。本文以按行獨立的EIV函數模型為背景，給出了利用RWTLS方法和附參數的條件平差方法在解決該問題的原理和解算方法，證明二者的平差結果是一致的，最后以兩個典型實例驗證。

2 附未知參數的條件平差模型及其解法

對于經典測量平差問題，設觀測值的總個數為m，必要觀測數為t，此時多余觀測數r＝m－t，若引入u個獨立的參數，可以列出c＝r＋u個條件方程式，用表示觀測值真值表示參數，函數模型可表示為

由于觀測值有誤差，從而導致參數也含有誤差，因而也稱為EIV模型［11］。設觀測值Δ（L表示觀測值，Δ表示誤差），測量平差的目的就是找到最佳估計值經典測量平差理論以Δ服從數學期望為零的正態分布為前提，以C［L］∈Rm×m表示觀測值的協方差陣，L的概率密度函數為

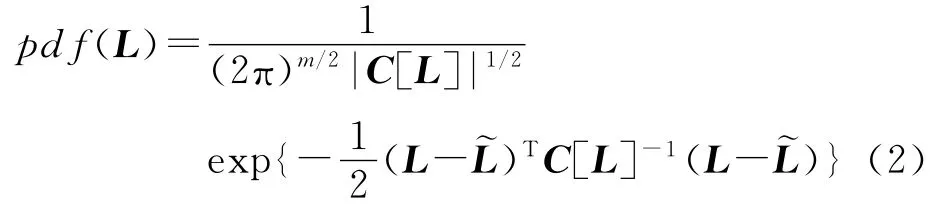
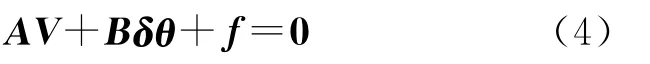
式中

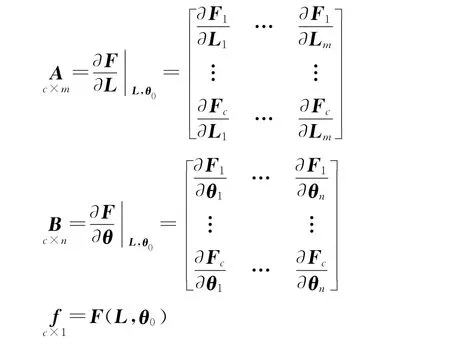
綜合式（3）、式（4）得到附參數的條件平差模型

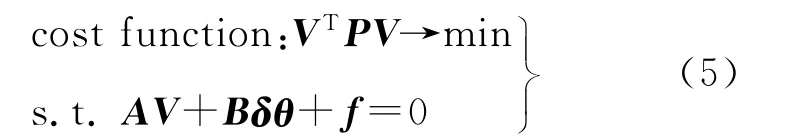
式（5）是一個求條件極值問題，按拉格朗日乘數法求條件極值的原理

式中，K∈Rc×1表示聯系數，將上式分別求V、δθ、K偏導并令其等于0，得到［1］

根據誤差傳播定律得到參數的協方差陣為

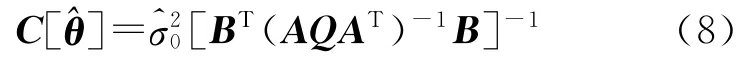
用df表示自由度，在經典測量平差問題中等于多余觀測數，即df＝r＝c－u，單位權中誤差為

3 按行獨立的加權總體最小二乘方法

簡單總體最小二乘問題通常可表示為求解一個Y≈Dθ形式的超定方程，若在函數模型中引入全部參數，此時u＝t，條件方程個數c＝r＋u＝m，即條件方程的個數等于觀測值的個數，若只考慮參數的誤差，將式（1）在參數初值處線性化，式（4）可寫成

此時，B∈Rm×n；δθ∈Rn×1；f∈Rm×1。由于m≥n，因此求解δθ的問題是一個求解超定方程解的問題。僅考慮f的誤差，在ΔfTΔf→min準則下的估計稱為簡單最小二乘估計，同時考慮B和f的誤差在tr（ΔBTΔB）＋ΔfTΔf→min準則下的參數估計稱為簡單TLS估計，得到的參數分別為［11］

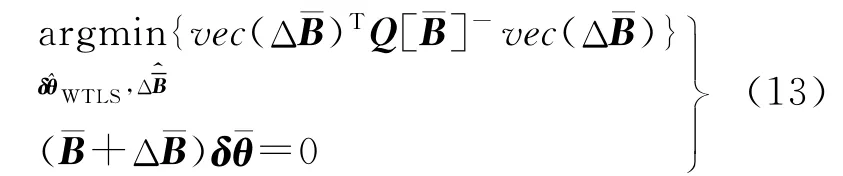
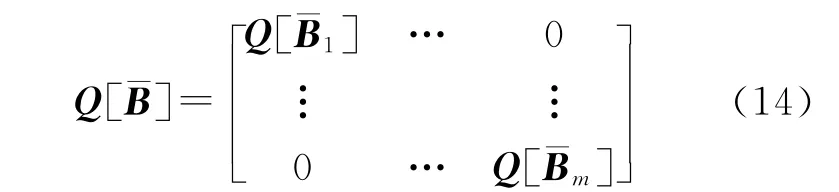
文獻［11］將WTLS的解算分成兩個計算步驟，簡化為求解一個無約束條件的極值問題，用數值迭代計算來實現。其核心思想是不直接求系數矩陣每個元素的改正值，而是先假定參數固定，僅考慮系數矩陣的方差，經誤差的線性傳播得到殘差的方差，用殘差的加權最小二乘代替系數矩陣元素的加權最小二乘，得到參數的估值，然后進一步求出系數矩陣元素的改正值，經迭代直至收斂。令表示殘差，若不考慮參數的誤差，殘差的協因數陣為

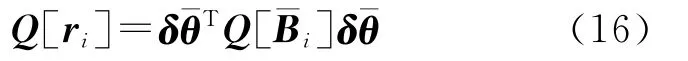
此時Q［ri］不再是奇異矩陣，原問題等價于以下子問題

然后得到參數和系數矩陣的改正數

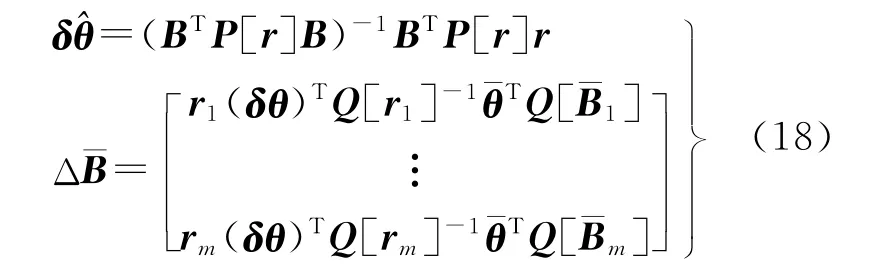
若要進一步求觀測值的改正數，顧及式（5）、式（10）得到

根據式（19）無法得到V的唯一解，根據最小二乘準則VTPV＝min（P＝Q－1表示觀測值的權陣），相當于經典條件平差問題，得到觀測值的改正數［1］

4 一致性證明及分析

由式（5）和式（10）得到以下關系

根據誤差傳播定律，得到殘差協因數陣的表達式應為

在總體最小二乘方法中，由于不求Ai，此時殘差的誤差不宜采用式（22）計算，若用上標“～”表示真值，則殘差與系數矩陣和觀測值之間的關系表示為

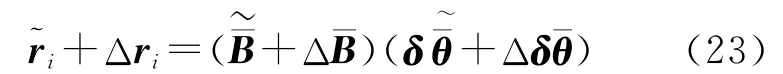
忽略高次項，得到真誤差之間的關系

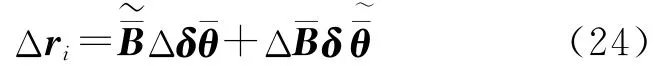
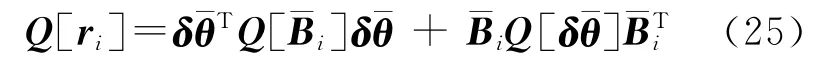
在數值計算過程中，通常先考慮其中的一項誤差，即固定參數或固定系數矩陣，通過迭代方法實現。在經典間接平差模型中，是不考慮系數矩陣的誤差，先求出參數的改正值后再更新系數矩陣然后進行下一次迭代。而在總體最小二乘迭代算法中固定參數值，得到殘差的近似協因數陣后再求參數，然后迭代。若采用式（22）計算殘差的方差并假設各行獨立，得到殘差向量的協因數陣為Q［r］＝AQAT，顧及P［r］＝Q［r］－1，代入式（18）得到

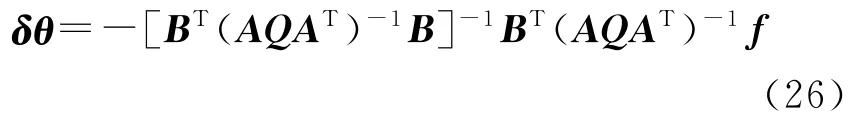
式（26）與式（7）的解析表達式相同，從而證明RWTLS與附參數的條件平差法的結果一致。若不采用式（22）計算殘差的方差而按式（16）計算，由于滿足式（21）的線性關系，兩種計算方法得到的殘差的協因數陣相等。無論是殘差的方差還是系數矩陣元素的方差都是由觀測值的誤差傳播得到，均滿足誤差傳播律，因而RWTLS的結果與附參數的條件平差結果一致。下面針對幾種特殊情況來說明：

（1）A＝I的情況（I為單位矩陣），此時的問題為經典間接平差問題，根據誤差傳播原理，此時殘差的權即為觀測值的權，代入兩種計算方法的參數表達式，得到的結果一致。

此時即為簡單總體最小二乘問題，將Q［r］＝I代入式（18）中，得到兩種方法的計算結果一致，這符合文獻［12］的結論，即當系數矩陣的所有元素均服從獨立等精度分布時，TLS方法與經典最小二乘方法的估計結果一致。

（3）精度評定問題，按上述計算原理，RWTLS的單位權中誤差的計算式應為

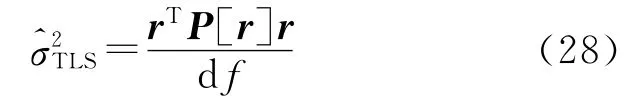
5 算 例

5.1 經典測量平差算例

如圖1水準網，其觀測值和已知數據見表1，為保證系數矩陣各行之間不相關，先按經典間接平差方法列出誤差方程，觀測值的權取路線長度的倒數。然后按下面的計算過程進行加權總體最小二乘解算，計算結果取小數點后5位有效數字，兩種方法得到的參數和及其中誤差見表2，數據表明二者的結果是完全一致。

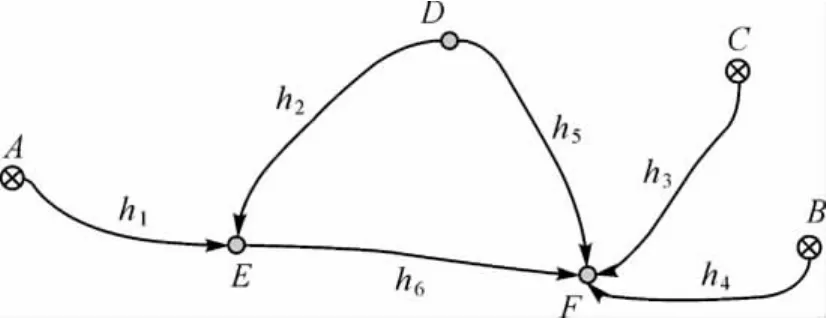
圖1 水準控制網形Fig.1 The configuration of a level control network

表1 觀測數據和已知數據Tab.1 Measurements and known data

表2 兩種方法得到的參數及其中誤差Tab.2 Estimated value and covariance with two methods m

（1）先取參數的初值HE＝29.980、HF＝30.877、HD＝30.121。按傳統間接平差原理得到誤差方程，此時殘差等于觀測值的改正數：r＝Bδθ－f，其中

（2）按簡單TLS方法得到參數初值。

（3）為了得到殘差的協因數陣，先計算f的協因數陣

（4）得到殘差的協因數陣

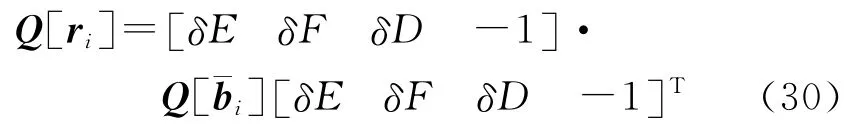
式中

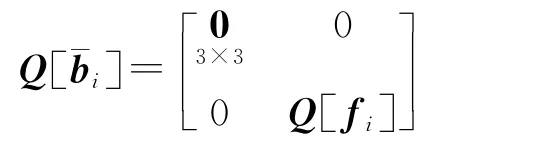
（5）求出參數，本算例由于殘差的誤差不受參數影響，不需要迭代。

5.2 最小二乘擬合算例

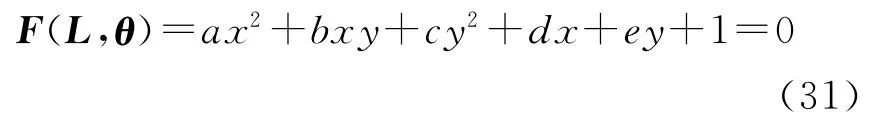
式中

將各點分別線性化

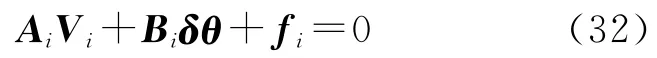
式中

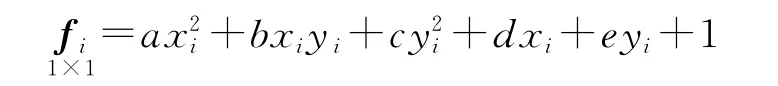
將上面的方程作為約束條件并考慮觀測值的權后得到附參數的條件平差的解算結果，由于Ai的系數與參數有關，因此也需要迭代計算。而在進行加權總體最小二乘計算時，需要得到的協方差陣，而的協方差陣是觀測值傳播得到的，其計算式為

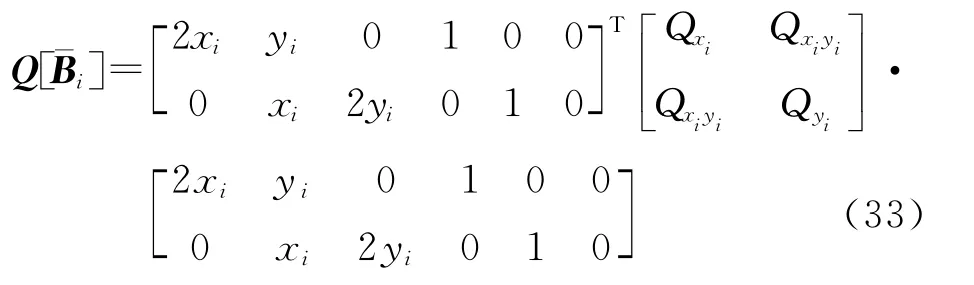
根據上述計算步驟，取簡單TLS的結果為初值，以‖δθ‖＜10－8作為迭代結束標志，本算例一般經3～4次迭代即可收斂，模擬1000次，兩種方法得到參數及其誤差的差值都在10－9數量級以下，說明主要是數值計算誤差。表3是隨機選取的一組觀測數據，解算結果見表4（取小數點后6位有效數字），表明估計結果完全一致。

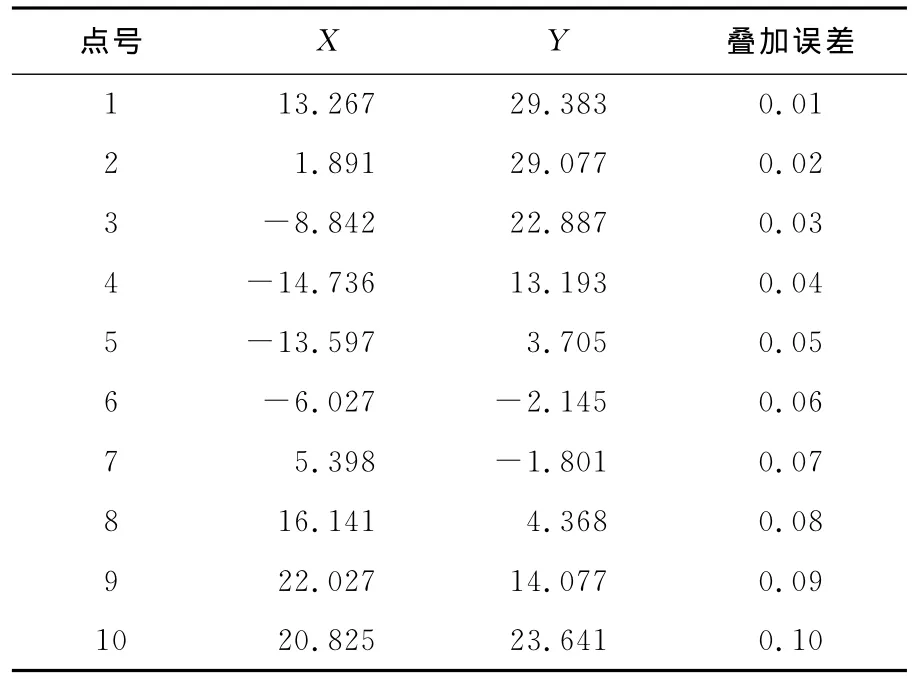
表3 模擬觀測數據Tab.3 The simulated measurements 像素

表4 不同方法的估計結果Tab.4 The results estimated by different methods

5.3 算例分析

以上選用了兩個比較典型的算例，算例1選用經典間接平差問題并且采用實測數據，由于水準測量的條件方程本身就是線性的，可以避免線性化對估計結果可能造成的影響，計算過程中不需要迭代。第2個算例選擇曲線擬合問題，采用不等精度的模擬數據，并采用迭代方法來求解，兩個算例得到的參數值及其方差完全一致。結合前面的理論分析可知：加權總體最小二乘與經典附參數的條件平差是同一模型的兩種不同解法。附參數的條件平差法以一個等式條件為約束，以原始觀測值的加權最小二乘條件為目標函數，加權總體最小二乘是以加權增廣系數矩陣的最小二乘條件為目標函數，以一個齊次線性方程為約束條件，而在計算中，將每行元素的改正數和對應的方差轉換為等價的殘差和對應的權，而這些誤差均是由觀測值的誤差傳播得來的，因而估計結果是一致的。但有些研究成果表明二者的結果并不完全一致，這可能是以下原因造成的：① 若增廣系數矩陣各元素服從獨立等精度分布，則簡單TLS估計和LS估計結果應一致，但實際應用中由于矩陣元素有很多常數，導致每個元素并非服從獨立等精度分布，從而引起差異；② 假設元素之間按行或按列獨立，殘差等精度等，而未考慮元素之間準確的相關關系；③ 未進行迭代計算；④ 單位權中誤差的計算方法不一致。

6 結 論

（1）對于EIV問題，加權總體最小二乘與經典附參數的條件平差問題估計結果一致，二者是同一測量平差問題的兩種不同解法。

（2）在進行加權總體最小二乘時，關鍵在權陣的選取，必須分清觀測值、參數、系數矩陣元素、殘差之間的誤差傳播關系，特別是矩陣元素的方差，否則將會導致總體最小二乘方法與經典平差結果不一致。

（3）由于RWTLS估計方法中，殘差與參數初值有關，因此需要迭代計算，而且需要注意參數初值可能導致的迭代發散問題。

（4）兩種估計方法雖然在理論上是一致的，但計算的復雜程度不相同，建議根據不同的函數模型選用平差方法。對于經典大地測量問題，由于線性化后系數矩陣元素的誤差關系復雜，建議選用原有經典平差方法。而對于數字攝影測量、三維激光掃描數據等中的數據擬合、坐標變換、核線估計等問題，系數矩陣大多只包含觀測值且按行分塊獨立，則選用RWTLS方法更為方便。

［1］ YU Zongcou，YU Zhenglin.Principle of Surveying Adjustment［M］.Wuhan：Publishing House of Wuhan Technology University of Surveying and Mapping，1990.（於宗儔，于正林.測量平差原理［M］.武漢：武漢測繪科技大學出版社，1990.）

［2］ ZHU Jianjun，SONG Yingchun.Progress of Modern Surveying Adjustment and Theory of Data Processing［J］.Geotechnical Investigation and Surveying，2009，37（12）：1－5.（朱建軍，宋迎春.現代測量平差與數據處理理論的進展［J］.工程勘察，2009，37（12）：1－5.）

［3］ OU Jikun.Uniform Expression of Solutions of Ill－posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights［J］.Acta Geodaetica et Cartographica Sinica，2004，33（4）：283－288.（歐吉坤.測量平差中不適定問題解的統一表達與選權擬合法［J］.測繪學報，2004，33（4）：283－288.）

［4］ OUYANG Wensen，ZHU Jianjun.Expanding of Classical Surveying Adjustment Model［J］.Acta Geodaetica et Cartographica Sinica，2009，38（1）：12－15.（歐陽文森，朱建軍.經典平差模型的擴展［J］.測繪學報，2009，38（1）：12－15.）

［5］ FENG Guangcai，ZHU Jianjun，CHEN Zhengyang，et al.A New Approach to Inequality Constrained Least－squares Adjustment［J］.Acta Geodaetica et Cartographica Sinica，2007，36（2）：120－123.（馮光財，朱建軍，陳正陽，等.基于有效約束的附不等式約束平差的一種新法［J］.測繪學報，2007，36（2）：120－123.）

［6］ PENG Junhuan，ZHANG Yali，ZHANG Hongping，et al.The Solution of Inequality－contrained Least Squares Problem and Its Statistical Properties［J］.Acta Geodaetica et Cartographica Sinica，2007，36（1）：50－55.（彭軍還，張亞利，章紅平，等.不等式約束最小二乘問題的解及其統計性質［J］.測繪學報，2007，36（1）：50－55.）

［7］ LU Tieding，TAO Benzao，ZHOU Shijian.Modeling and Algorithm of Linear Regression Based on Total Least Squares［J］.Geomatics and Information Science of Wuhan University，2008，33（5）：504－507.（魯鐵定，陶本藻，周世健.基于整體最小二乘法的線性回歸建模和解法［J］.武漢大學學報：信息科學版，2008，33（5）：504－507.）

［8］ LU Jue，CHEN Yi，ZHENG Bo.Applying Total Least Squares to Three Dimensional Datum Transformation［J］.Journal of Geodesy and Geodynamics，2008，28（5）：77－81.（陸玨，陳義，鄭波.總體最小二乘方法在三維坐標轉換中的應用［J］.大地測量與地球動力學，2008，28（5）：77－81.）

［9］ SCHAFFRIN B，WIESER A.On Weighted Total Leastsquares Adjustment for Linear Regression［J］.Journal of Geodesy，2008，82（7）：415－421.

［10］ SCHAFFRIN B，FELUS Y A.On the Multivariate Total Least－squares Approach to Empirical Coordinate Transformations——Three Algorithms［J］.Journal of Geodesy，2008，82（6）：373－383.

［11］ GOLUB G H，VAN LOAN C F.An Analysis of the Total Least Squares Problem［J］.SIAM Journal on Numerical Analysis，1980，17：883－893.

［12］ VAN HUFFEL S，VANDEWALLE J.The Total Least Squares Problem［M］.Philadelphia：SIAM，1991.

［13］ MARKOVSKY I，VAN HUFFEL S.Overview of Total Least Squares Methods［J］.Signal Process，2007，87：2283－2302.

［14］ MARKOVSKY I，RASTELLO M，PREMOLI P，et al.Element－wise Weighted Total Least Squares Problem［J］.Computational Statistics and Data Analysis，2006，50：181－209.

［15］ MüHLICH M，MESTER R.Subspace Methods and Equilibration in Computer Vision［C］∥Proceedings of 12th Scandinavian Conference on Image Analysis.Stavanger：［s.n.］，2001：415－422.

［16］ SCHAFFRIN B，FELUS Y A.On Total Least－squares Adjustment with Constraints［C］∥Proceedings of Windows on the Future of Geodesy.Berlin：IAG－Symp，2005：417－421.