基于星型結構的虛擬參考站網絡實時動態測量關鍵算法研究

沈雪峰，高成發，潘樹國

1.東南大學交通學院，江蘇南京210096；2.東南大學儀器科學與工程學院，江蘇南京210096

1 引 言

隨著網絡技術的飛速發展，以虛擬參考站技術（VRS）［1－2］為代表的網絡RTK技術有效地彌補了常規RTK的不足，成為GNSS厘米級高精度實時定位的一種重要手段。與常規RTK相比，網絡RTK技術具有精度和可靠性高、服務范圍廣、精度分布均勻等優點［3－4］。隨著互聯網與移動通信技術的普及，作為最具代表性的網絡RTK技術——VRS技術，其性能越來越穩定，應用范圍越來越廣泛［5－7］。常規網絡RTK技術一般采用三角形結構進行單基線模式模糊度網解［8－10］和誤差建模［11－12］。這種三角形網絡結構也有一些不足之處，特別是相對于作為將來主要發展趨勢的大規模、長基線網絡RTK系統，該方式沒有充分利用多參考站冗余觀測信息，降低了系統模糊度解算速度以及改正數的可靠性，從而嚴重影響流動站定位速度及可靠性。為了確保大規模網絡RTK定位的精度與可靠性，筆者提出了構建星型結構的VRS網絡來取代傳統VRS三角形網絡結構，同時針對星型結構提出了相應的VRS關鍵算法，并進行了試驗分析與比較。

2 星型拓撲結構VRS網絡構建

目前，網絡RTK系統都是在連續運行參考站系統（CORS）基礎上建立起來的。CORS基準站的分布情況將直接影響到基線模糊度解算效率和精確誤差建模。在GPS差分定位中，影響定位精度的誤差主要是距離相關誤差，因此基準站間距離和網絡分布情況均會影響誤差建模的精確性［13］，為此構建最優的基準站網絡極其關鍵。由于傳統VRS技術是以三角形為基本解算單元［13－14］，因此不規則三角形網絡方法常常用于CORS基準站網絡的構建，其中以Delaunay三角網最佳［13－14］。

傳統VRS技術，以用戶所在三角形為基本解算單元建立網絡改正模型，它僅選擇用流動站所在的三角形區域的3個參考站及基線數據，建立覆蓋三角形區域的改正計算模型。如圖1所示，圖中陰影部分區域就是其中的基本解算單元。

這種解算單元能保證改正區域與流動站最大程度的符合，只要該三角形解算單元網絡初始化正常，就能保證較優的網絡改正精度和可靠性，同時也不受其他單元初始化錯誤的影響。但在實踐過程中筆者發現這種三角形網絡結構也有一些不足之處，主要表現在：① 它采用的是單基線解算模式，沒有充分利用多參考站多余觀測信息，導致對于長基線和低高度角衛星的模糊度固定時間較長，不利于大規模基準站網絡的初始化；② 獨立基線信息較少（2條基線），因此限制了內插計算時可供選擇的數學模型（模型參數≤2）的精確性［15］，因而在一定程度上影響了改正數的精度，特別是對于高程差異較大區域的定位精度會有所降低；③ 對于基本解算單元以外的區域，其改正精度隨距離的增加大幅下降。

本文針對傳統VRS技術的基本解算單元的不足，在Delaunay三角網的基礎上，提出一種星型結構的VRS網絡基本解算單元。如圖2所示，為一個星型結構的基本解算單元。

星型VRS網的建立方法是先將整個CORS網絡按Delaunay三角網構網原則建立不規則三角網，然后以參考站關聯的基線數以及參考站位置作為選取原則，選擇其中n個參考站作為中心參考站，將與任一中心參考站形成Delaunay三角網的其余參考站作為輔助參考站，形成一個星型結構基本解算單元，從而可以將整網分成n個子網，而這些子網以星型拓撲結構構建，以中心參考站命名，具體流程圖如圖3所示。

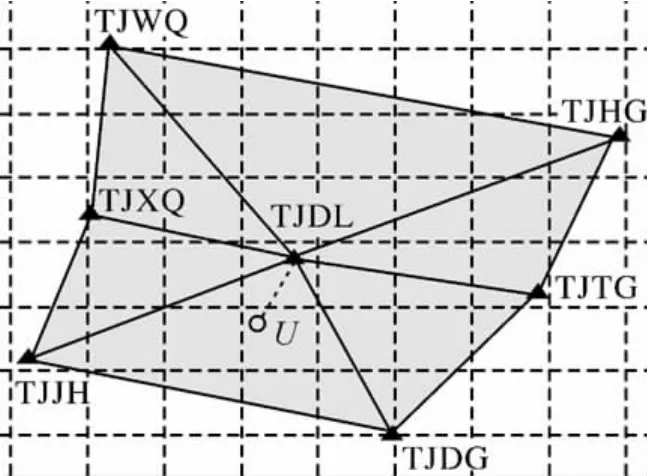
圖2 星型基本解算單元Fig.2 Basic solving unit of star

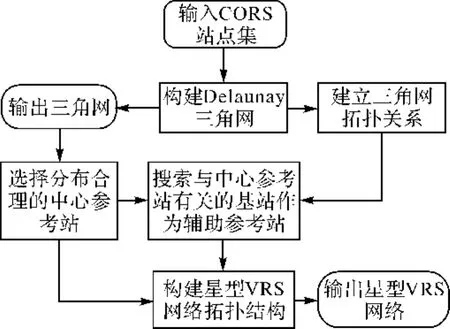
圖3 星型VRS網絡結構生成流程Fig.3 Flow chart for the growth of star structure VRS network

如圖4所示，選擇江蘇CORS的7個參考站先建立Delaunay三角網，然后選擇其中的參考站NJZX站和NJTS站作為中心參考站，即可形成兩個星型拓撲結構的基本解算單元，即解算單元NJZX和解算單元NJTS，如圖5所示。

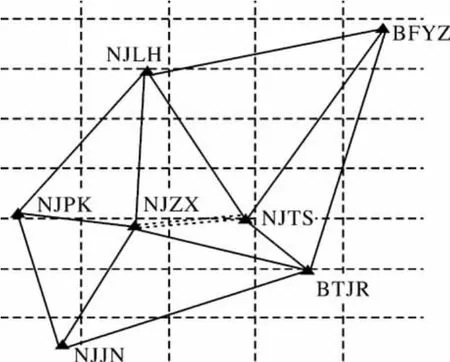
圖4 JSCORS站分布圖Fig.4 Distribution of JSCORS stations

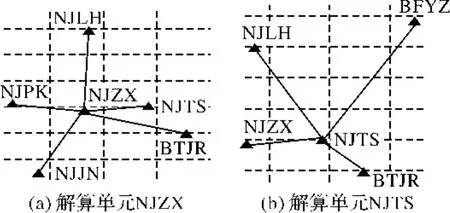
圖5 JSCORS星型基本解算單元Fig.5 Basic solving unit of star of JSCORS

采用上述星型拓撲結構作為基本解算單元，它既繼承了傳統VRS三角形解算單元改正相關性強、共視衛星多的優點，又能充分利用多基站多余觀測信息，提高模糊解算效率，使得內插模型靈活多樣，保證了內插模型具有較好的數據冗余，提高了誤差改正的精度和可靠性，同時這種星型基本解算單元有唯一的參考衛星，解算基線獨立。

3 星型VRS網絡模糊度解算策略

對于大規模參考站網絡（CORS）而言，網絡模糊度解算主要是指參考站間的基線模糊度解算。無論是建立誤差模型，還是計算高精度的綜合誤差，參考站間基線模糊度解算［8－10］是重要的前提條件。

對于傳統VRS三角形解算單元來說，一般采用單基線解算模式，但這種單基線解算模式有其一定的不足。由于在三角形解算單元中，相鄰的兩條基線估計模糊度時存在共同的參數。該參數的估值誤差對于低高度角以及長基線模糊度解算來說影響很大，大大影響了基線模糊度的解算速度，嚴重影響網絡RTK系統的初始化。

本文提出的星型基本解算單元較傳統VRS三角形解算單元具有更多的多余觀測值。采用多基線解算模式，充分考慮多基線的共有參數，加快L1模糊度解算速度，特別是加快了長基線以及低高度角衛星模糊度解算速度，以利于大規模網絡RTK系統的初始化。

采用兩步法［10］解算策略：① 由于寬巷雙差模糊度能在較短時間內固定且不同衛星間相關性較小，因此直接采用單基線模式，利用寬巷組合的長波特性快速固定寬巷模糊度，本文不再詳述；②本文重點介紹采用多基線模式，利用無電離層組合、寬巷模糊度與L1、L2模糊度之間的關系解算出L1、L2雙差模糊度ΔΔN1、ΔΔN2。

對于星型解算單元中每一條基線在固定寬巷模糊度之后，都可采用無電離層組合分離出L1雙差模糊度，其計算公式為

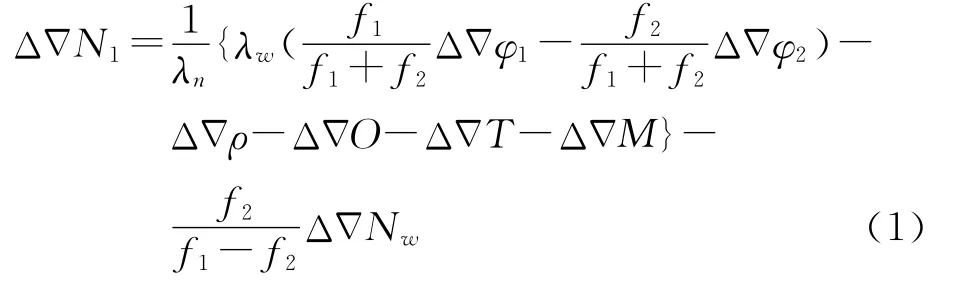
由式（1）可見，采用無電離層組合可以有效地消除電離層的影響。其中軌道誤差O、多路徑效應M可以忽略不計，因此影響精度的主要為對流層延遲，雙差對流層延遲可表示為

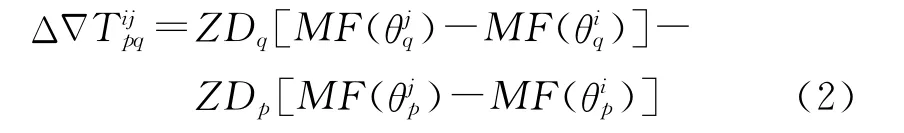
式中，ZDq和ZDp分別為p站與q站的天頂延遲；MF（·）為投影函數。

由于在星型解算單元中共有中心參考站的信息，故可對式（2）進行如下處理，即分離出中心參考站q的待估計參數天頂對流層延遲ZDq，如式（3）所示。

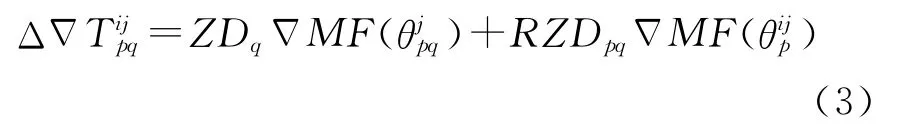
式中，RZDpq為相對天頂對流層延遲。

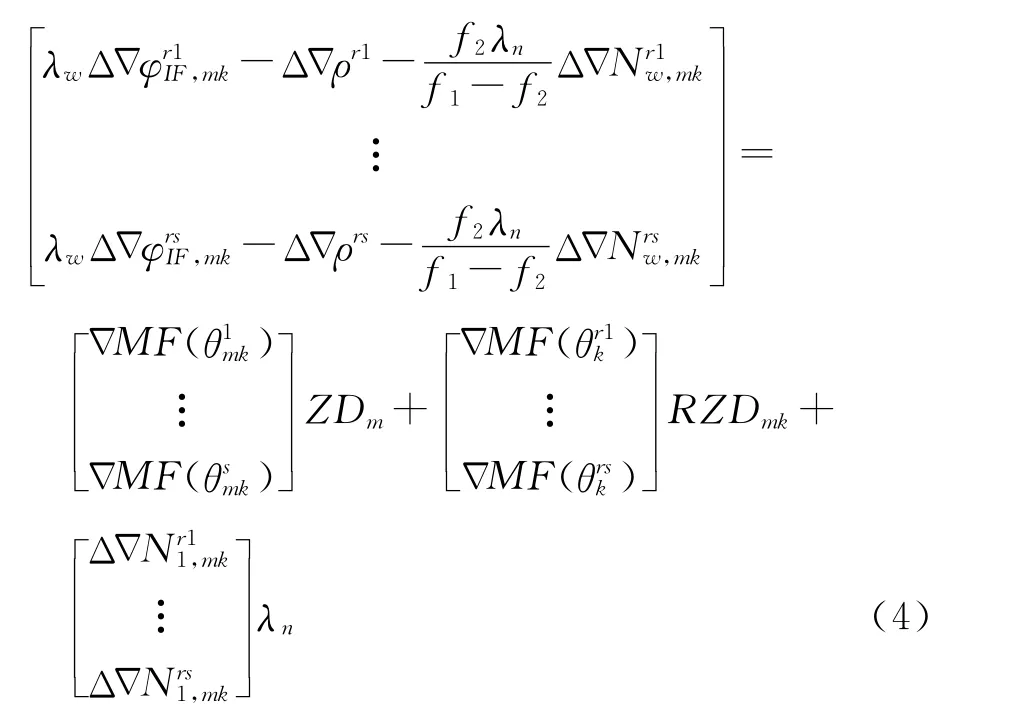
故任意第k條基線多衛星模糊度解算模型如下

式中，r為參考衛星；s為非參考衛星；m為中心參考站；k為輔助參考站。

在此基礎上，采用以下策略：首先選擇星型基本解算單元中基線最短的基線進行模糊度解算，構建卡爾曼濾波器［10］，即可快速估計出中心參考站m的天頂對流層延遲ZDm、m與k兩站相對天頂對流層延遲RZDmk以及模糊度浮點解。

由于ZDm變化非常緩慢，可把它看做隨機游走過程，故設定ZDm與RZDmk的狀態轉移噪聲方差為1cm2／h、2cm2／h，其初值由Hopfield模型獲得；模糊度的狀態轉移噪聲為零，其狀態噪聲方差也為零。

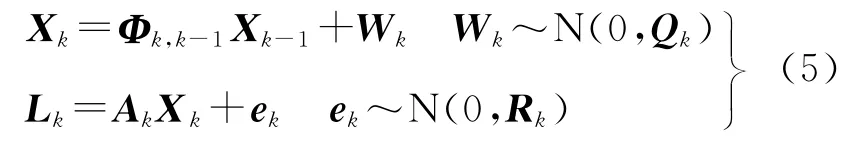
式中，Xk為tkΔ時刻的狀態向量；Xk＝［ZDmRZDmkΔN1… ］T；Lk為觀測向量，

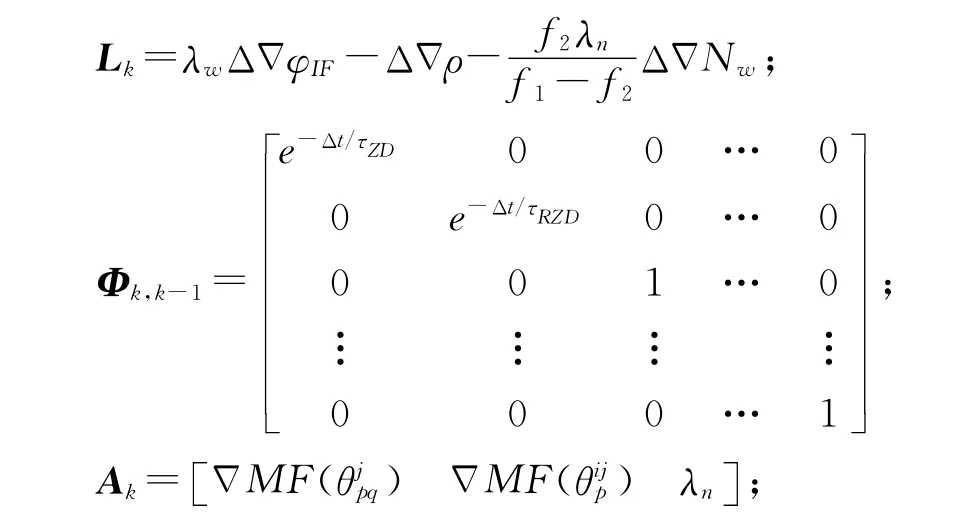
Qk為觀測誤差方差陣，采用基于高度角信息的隨機模型［11］。

由于星型基本解算單元具有同一中心參考站m，所以可以將已估計出的天頂對流層延遲ZDm實時應用于其余基線的解算，加快模糊度浮點解解算效率，構造新的卡爾曼濾波器。此時只估計相對天頂對流層延遲RZDmk和模糊度浮點解，相關的狀態噪聲方差與觀測值隨機模型與第一個濾波器一致，與最后采用LAMBDA算法加快模糊度固定速度。

4 星型VRS網絡改正數計算模型

在VRS網絡模糊度固定之后，則需要進行VRS網絡誤差改正數的計算建模［16－17］。目前VRS的誤差改正數計算模型大多采用常規內插模型，就是將所有誤差綜合起來進行綜合誤差的內插或擬合計算。但是由于多種誤差之間的變化規律及相關特性存在差異，使用單一修正模型計算VRS改正數的方法在精度和可靠性上均存在不足。為此，必須對VRS誤差分離進行分類建模，以利于VRS誤差改正數的精化。

4.1 電離層改正數星型內插模型（SIM）

由于電離層延遲誤差的色散性，在固定模糊度之后，采用雙頻相位觀測值可以計算參考站網絡各基線上的電離層延遲，忽略觀測噪聲和高階電離層延遲誤差的影響，就可以得到基線上的電離層雙差改正數，如下式

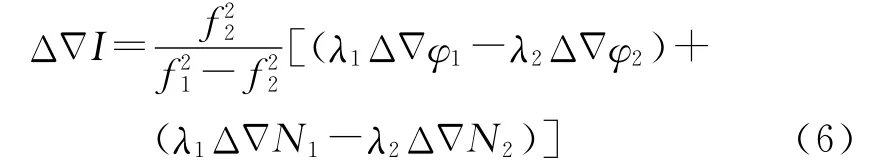
由于線性內插法LIM可以很好地逼近電離層平靜時段電離層延遲在參考站網絡區域范圍內的空間分布相關特征，且具有較強的適用性，尤其在中緯度地區，其改正數精度可達2～4cm［15］。故本文首先利用LIM模型來計算電離層雙差改正數，由此可建立基于星型解算單元的LIM模型，如式（7）所示。

式中

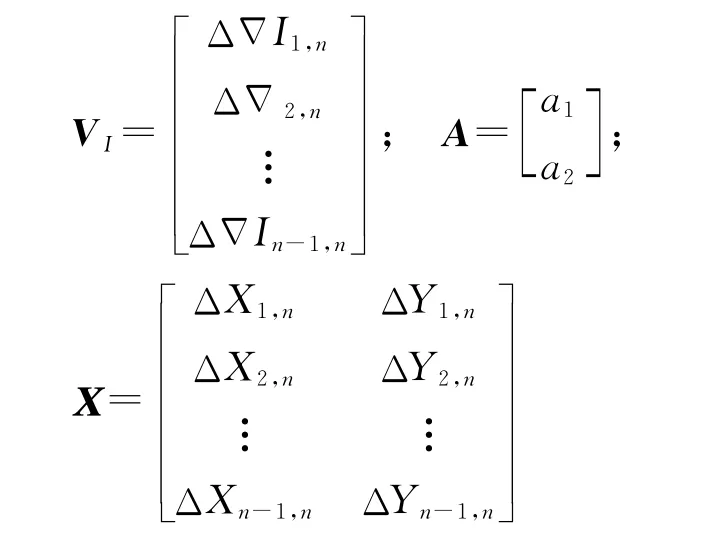
式中，i＝（1，…，n－1）；n代表中心參考站；1，…，n－1代表n－1個輔助參考站。如圖6所示，a1、a2為內插系數，ΔXi，n、ΔYi，n為平面坐標差。

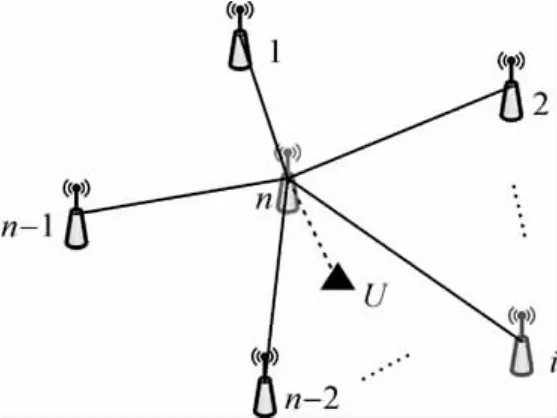
圖6 星型解算單元站點分布圖Fig.6 Distribution of stations in solving unit of star

則對于用戶u，根據LIM特性以及式（7）可得到電離層雙差改正數的空間相關線性項即

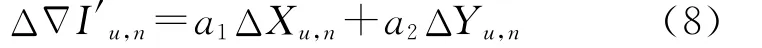
在此基礎上，依次以i＝（1，…，n－1）作為監測站，其余參考站作為輔助站，由式（8）內插監測站i，可得到

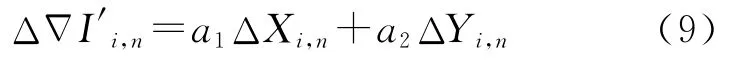
故可建立星型解算單元所有εi，n的擬合模型εi，n＝從而可得到用戶u的內插殘差項εu，n，則用戶其電離層改正數為

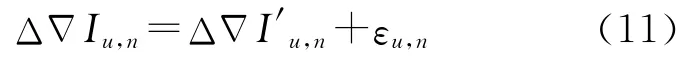
4.2 對流層改正數星型內插模型（SHM）

由于對流層延遲誤差受高程因子影響顯著，使其在水平方向和高程方向空間相關特性存在明顯差別，因此參考站與流動站間的高程差異會引起對流層誤差改正數中存在系統偏差的影響，使對流層改正精度降低，故對流層改正數內插建模需要考慮高程偏差。本文提出構建三維內插模型，以建立對流層改正數星型網絡內插模型。

針對圖6的星型解算單元，利用式（3）和式（4）可得到任意基線i、n的對流層雙差改正數，即

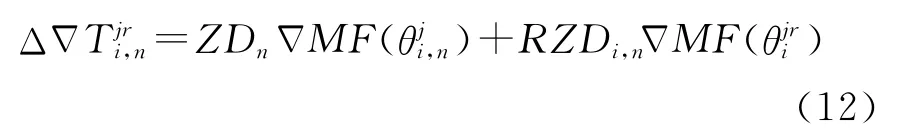
并假設任意改正數滿足下式

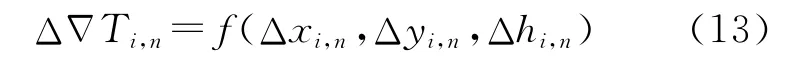
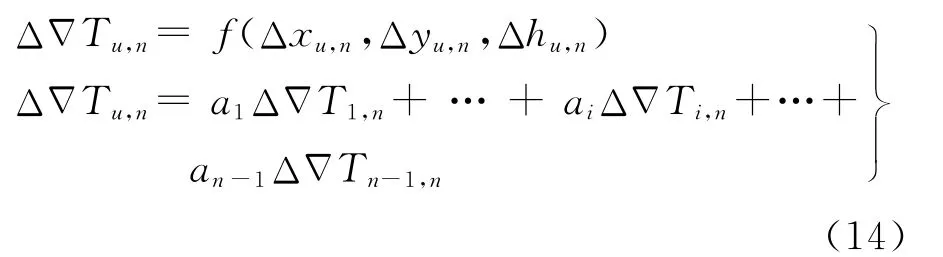
并在LCM模型上［16］添加高程因子h，設其內插系數ai滿足以下約束條件

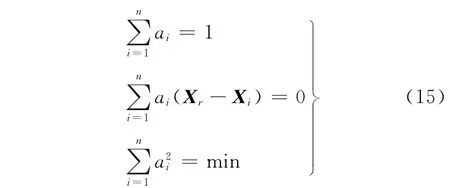
5 數據處理試驗與分析比較

5.1 星型VRS網絡模糊度固定試驗與分析

采用重慶市國土資源GNSS網（CQCORS）的觀測數據進行分析，分別選擇南川站（NACH）、南岸站（NAAN）、長壽站（CHSH）、豐都站（FEDU）、彭水站（PESH）、武隆站（WULO）共6個基站，以南川（NACH）作為中心參考站，組成星型VRS網絡，如圖7所示。該網絡中所有參考站均使用天寶天線TRM55971和參考站型接收機。試驗數據采用2010－11－10T10：00：00—11：59：59；采樣間隔1s。根據圖8所示的高度角變化圖，選擇高度角最大的PRN15衛星作為參考衛星。選擇3個代表低、中、高高度角衛星與PRN15組成3組衛星對PRN18－15、PRN21－15、PRN29－15。

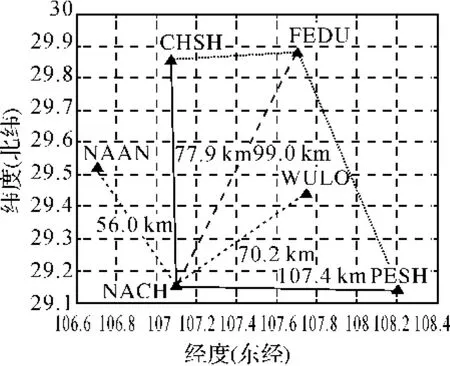
圖7 CQCORS參考站分布圖Fig.7 Distribution of JSCORS stations

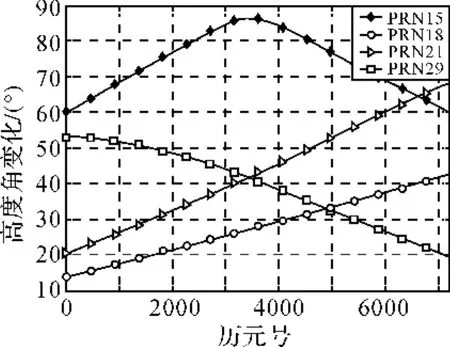
圖8 衛星高度角隨歷元變化圖Fig.8 The change of elevation of satellites with epochs

本文主要分析L1雙差模糊度的固定。故分別采用單基線解算模式以及本文提出的多基線解算模式進行分析比較。其中單基線解算模式是對星型VRS網絡的每一條基線進行模糊度解算。由于單基線模糊度固定時間主要是受較低高度角衛星模糊度收斂的影響，因此以PRN18－PRN15這一衛星對進行分析，其模糊度固定時間結果見表1所示。

而多基線解算模式是先選擇星型VRS網絡中最短基線NACH—NAAN（基線長56km）進行解算，估計出中心參考站BTJJ的天頂對流層延遲，并將其應用于其余基線，重新構建新的卡爾曼濾波器估計模糊度浮點解與相對天頂對流層延遲。同樣以PRN18－PRN15這一衛星對進行分析，其模糊度固定時間結果見表2所示。

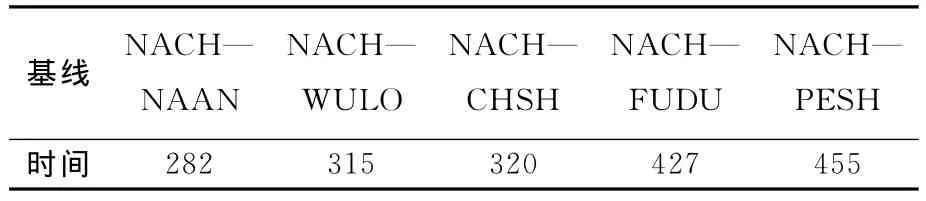
表1 單基線解算模糊度固定時間Tab.1 The fixed time of ambiguity resolution of single baseline s

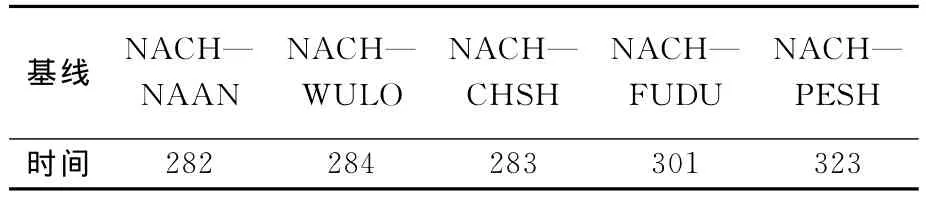
表2 多基線解算模糊度固定時間Tab.2 The fixed time of ambiguity resolution of multibaseline s

對比表1和表2、圖9可以看出，采用本文提出的針對星型解算單元的模糊度解算方式明顯比傳統VRS的單基線模糊度解算方式優越，它使得模糊度固定時間大大縮短。以基線NACH—PESH為例（如圖9所示），當方差比Ratio因子大于閾值時，可認為模糊度已固定，從圖9可以看出采用多基線解算模式固定速度明顯快于單基線解算模式。對比可以看出，采用常規單基線解算模式，隨著基線長度的增加，固定時間隨之快速增加，而采用星型多基線解算模式，其星型網元內各基線的L1模糊度的固定時間較為接近，有利于提高長距離、大規模網絡RTK系統的初始化速度。

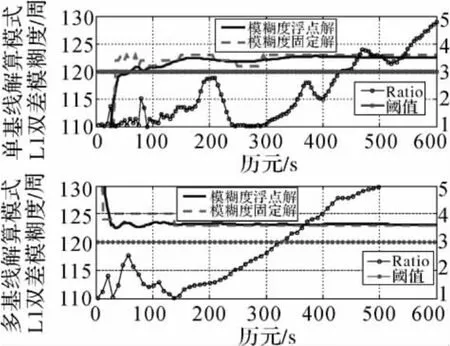
圖9 NACH—PESH兩種解算模式比較Fig.9 Compare of two resolution models for NACH—PESH

另外，無論是表1的結果，還是表2的結果都表明，長基線L1模糊度固定時間明顯長于較短基線。這是由于使用電離層無關組合中，模糊度與相對對流層延遲相關性較強，基線越長，相對對流層延遲越大，其誤差也越大，導致長基線上模糊度固定時間很長。

5.2 星型VRS網絡改正數計算模型試驗與分析

試驗網絡選取同樣的星型VRS網絡，以NACH作為中心參考站與輔助參考站CHSH、FEDU、PESH組成星型解算單元，以WULO（網內）、NAAN（網外）分別作為流動站，其高程差異分布見圖10，采用本文提出的SIM、SHM分別內插用戶電離層改正數、對流層改正數，由于傳統的內插模型內插效果基本一致［16］，故選擇具代表性的線性內插模型LIM，與之進行比較分析。

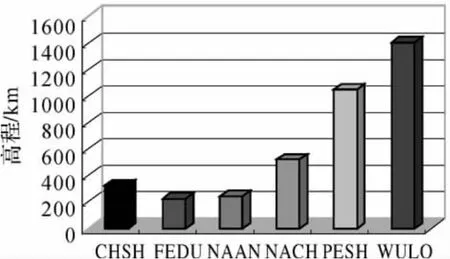
圖10 高程差異分布Fig.10 Difference of heights among stations

選取最具代表性的兩顆衛星進行分析比較，其中衛星PRN18為低高度角衛星（升星），PRN29為高高度角衛星（降星）。以誤差的最大值、平均值、中誤差作為統計指標，采用SIM與LIM內插電離層改正數的結果見圖11及表3，采用SHM與LIM內插對流層改正數的結果見圖12及表4。

圖11 LIM與SIM電離層改正數內插誤差變化圖Fig.11 The variation of double－differenced ionospheric biases for LIM and SIM

從圖11及表3可以看出，無論流動站是在網內還是網外，本文提出的SIM其內插精度一般在1cm左右，明顯高于傳統的LIM內插精度；當在網外時，傳統的LIM內插模型改正精度大幅下降，而SIM則下降不明顯，仍然保持在1cm左右。此外網內的內插精度都要高于網外的內插精度，當衛星高度角較低時，傳統的LIM內插精度遠遠低于本文提出的SIM模型，而高度角對SIM模型影響較小，SIM模型內插精度很穩定。

從圖12及表4可以看出，無論是對于低高度角衛星還是高高度角衛星，本文提出的SHM模型遠遠高于傳統的LIM模型，特別是對于低高度角衛星，LIM模型精度遠遠低于SHM模型的內插精度；此外可以看出對衛星高度角較高的衛星以及網內流動站內插時，其內插精度較高。

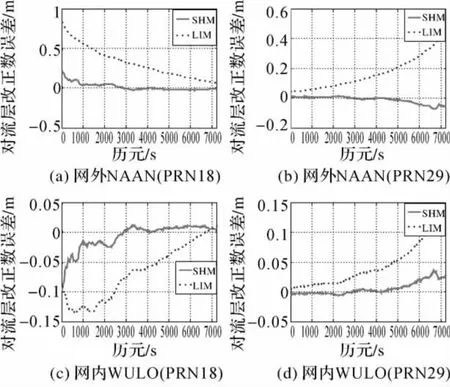
圖12 LIM與SHM對流層改正數內插誤差變化圖Fig.12 The variation of double－differenced tropspheric biases for LIM and SIM

表3 LIM與SIM兩種算法改正結果精度統計Tab.3 Statistic of correction accuracy between LIM and SIM m

表4 LIM與SHM兩種算法改正結果精度統計Tab.4 Statistic of correction accuracy between LIM and SHM m

6 結 論

試驗表明本文提出的星型VRS網絡多基線解算模式較傳統VRS單基線解算模式效率更高。由于星型VRS網絡改正數計算模型的靈活性，本文提出的試驗結果表明針對流動站電離層改正數生成的高精度星型內插模型SIM精度優于傳統模型，其內插精度穩定在1cm左右，而對流層改正數三維內插模型SHM可修正參考站與流動站高程差異引起的對流層誤差改正數中系統偏差的影響，其內插精度可保持在2cm左右，明顯優于傳統內插模型。

［1］ LANDAU L，VOLLATH U，CHEN X M.Virtual Reference Station Systems［J］.Journal of Global Positioning Systems.2002，1（2）：137－143.

［2］ TRIMBLE.Trimble Virtual Reference Station VRS［M］.Sunnyvale：［s.n.］，2001.

［3］ HUANG Dingfa，LI Chenggang，WU Yaoqiang，et al.Study of the Real－time Network Correction Generation［J］.Acta Geodaetica et Cartographica Sinica，2007，36（3）：256－261.（黃丁發，李成鋼，吳耀強，等.GPS／VRS實時網絡改正數生成算法研究［J］.測繪學報，2007，36（3）：256－261.）

［4］ KE Fuyang，WAND Qing，PAN Shuguo，et al.Key Algorithm and Technique of VRS Network RTK and Precision Analysis［J］.Journal of Astronautics，2009，30（3）：1287－1292.（柯福陽，王慶，潘樹國，等.VRS網絡RTK關鍵算法與技術及精度分析［J］.宇航學報，2009，30（3）：1287－1292.）

［5］ JENSEN A B O，CANNON M E.Performance of Network RTK Using Fixed and Float Ambiguities［C］∥Proceedings of the 2000National Technical Meeting of the Institute of Navigation.Anaheim：The Institute of Navigation，2000：797－805.

［6］ CHEN X M，HAN S W，RIZOS C，et al.Improving Realtime Positioning Efficiency Using the Singapore Integrated Multiple Reference Station Network（SIMCORSN）［C］∥Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation.Salt Lake City：The Institute of Navigation，2000：9－18.

［7］ HU G，ABBEY DA，CASTLEDEN N，et al.An Approach for Instantaneous Ambiguity Resolution for Medium to Long－range Multiple Reference Station Networks［J］.GPS Solution，2005，9（1）：1－11.

［8］ PAN Shuguo，WANG Qing，KE Fuyang，et al.Method for Integer Ambiguity Resolution in GPS Network RTK［J］.Journal of Southeast University：English Edition，2009，25（4）：491－495.

［9］ GAO Xingwei，LIU Jingnan，GE Maorong.An Ambiguity Searching Method for Network RTK Baselines between Base Stations at Single Epoch［J］.Acta Geodaetica et Cartographica Sinica，2002，31（4）：305－309.（高星偉，劉經南，葛茂榮.網絡RTK基準站間基線單歷元模糊度搜索方法［J］.測繪學報，2002，31（4）：305－309.）

［10］ ZHOU Letao，HUANG Dingfa，YUAN Linguo，et al.A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network［J］.Acta Geodaetica et Cartographica Sinica，2007，36（1）：37－42.（周樂韜，黃丁發，袁林果，等.網絡RTK參考站間模糊度動態解算的卡爾曼濾波算法研究［J］.測繪學報，2007，36（1）：37－42.）

［11］ HU G R，KHOO H S，GOH P C，et al.Development and Assessment of GPS VRS for RTK Positioning［J］.Journal of Geodesy，2003，77（5－6）：292－302.

［12］ TANG Weiming，LIU Jingnan，LIU Hui，et al.A Modified Combined Bias Interpolation Method for GNSS Network RTK［J］.Geomatics and Information Science of Wuhan University，2007，32（12）：1156－1159.（唐衛明，劉經南，劉暉，等.一種GNSS網絡RTK改進的綜合誤差內插方法［J］.武漢大學學報：信息科學版，2007，32（12）：1156－1159.）

［13］ ZOU R，LIU H，YAO Y B，et al.Application of Delaunay Triangulated Networks to Continuous Operational Reference System［J］.Journal of Geomatics，2005，30（6）：9－11.（鄒蓉，劉暉，姚宜斌，等.Delaunay三角網構網技術在連續運行衛星定位服務系統中的應用［J］.測繪信息與工程，2005，30（6）：9－11.）

［14］ ZHOU Letao，HUANG Dingfa，LI Chenggang，et al.Algorithm for GPS Network Construction Based on Spherical Delaunay Triangulated Irregular Network［J］.Journal of Southwest Jiaotong University，2007，42（3）：380－383.（周樂韜，黃丁發，李成鋼，等.基于球面Delaunay三角網的GPS網構造算法［J］.西南交通大學學報，2007，42（3）：380－383.）

［15］ LI Chenggang.Generation and Distribution Technique of Precise Differential Corrections for GPS／VRS Network［D］.Chengdu：Southwest Jiaotong University，2007.（李成鋼.網絡GPS／VRS系統高精度差分改正信息生成與發布研究［D］.成都：西南交通大學，2007.）

［16］ LI Chenggang，LI jie，YANG Li，et al.Ionospheric Disturbance Delay Correction Method for Reference Station Network over Mid ＆Low Latitude Region［J］.Science of Surveying and Mapping，2009，34（4）：27－29.（李成鋼，李杰，陽力，等.中低緯度地區連續運行參考站網絡電離層擾動修正技術研究［J］，測繪科學，2009，34（4）：27－29.）

［17］ DAI Liwen，HAN Shaowei，WANG Jinling，et al.A Study on GPS／GLONASS Multiple Reference Station Techniques for Precise Real－time Carrier Phase－based Positioning［C］∥Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation.Salt Lake City：ION Publications Department，2001：392－403.