1PN近似下脈沖星導航的觀測方程及精度分析

任紅飛，魏子卿，翟振和，吳富梅

1.信息工程大學測繪學院，河南鄭州450052；2.西安測繪研究所，陜西西安710054

1 引 言

觀測方程是處理脈沖星觀測數據的基礎，用脈沖星自主導航時，觀測方程的精度決定脈沖星導航的精度，也影響脈沖星星表參數的精化。反過來，高精度的脈沖星歷表參數又有利于提高觀測方程的精度，進而提高導航性能。高精度的觀測與參數精化是一個經長期觀測，相互促進的過程。

廣義相對論是現今最精確的引力理論。對于高精度的脈沖星導航而言，廣義相對論效應是必須考慮的因素，在相對論框架下給出觀測方程的高精度表達式是實現脈沖星精確導航的前提。文獻［1—2］分別推導了1階后牛頓（1PN）度規形式下的脈沖星計時表達式。比較而言，文獻［1］的推導更為嚴格，考慮了太陽引力場對信號傳播的彎曲效應，但推導過程與結論不夠準確。2005年，文獻［3］重新給出1PN度規形式下脈沖到達時間（TOA）的正確表達式，但沒有進行詳細推導。當前，脈沖星計時精度約為1μs，脈沖星導航也處于試驗驗證階段。受脈沖星觀測精度的限制，一些影響相對較弱的誤差源還未被考慮。隨著觀測技術的改進，將需要分析更多誤差源對觀測的影響。筆者通過分析以上文獻的研究結論，并參考其他相關文獻［4－17］，完整推導1PN度規形式下脈沖星導航的觀測方程，以此為基礎，對影響導航性能的主要因素進行分析。

2 X射線脈沖星導航的觀測方程

用X射線脈沖星為飛行器導航時，通常的處理方式是：將空間飛行器觀測的TOA轉化至某個基點，與基點處的TOA模型組成差分方程。在當前的研究中，一般以太陽系質心（SSB）為基點，將飛行器處的TOA轉換至SSB。

為推導1階后牛頓（1PN）度規形式下脈沖星導航觀測方程，在此只考慮太陽系以內天體的相對論效應，而將太陽系以外天體的相對論效應視作常量［1－2］。

脈沖星的脈沖是由一個周期內的光子累積而成的，每個光子在空間沿自己的世界線傳播。根據相對論理論，電磁信號在時空中傳播的世界線為零測地線，即時空間隔為零。其有表達式為

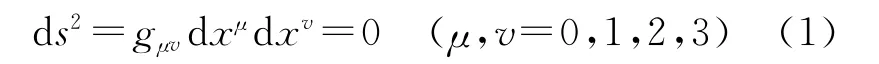
式中，ds2為線元的平方；dxμ、dxv為坐標增量；gμv為時空度規，是觀測者處時空位置的函數，由愛因斯坦場方程求解得到。由于愛因斯坦場方程的高階非線性和星體質能分布的復雜性，一般不可能得到gμv的嚴格解。實際應用中所采用的時空度規都是在某種近似條件下得到的結果。

對于太陽系這樣的弱場、低速時空，IAU在第24屆決議中推薦使用后牛頓度規，該度規滿足線性疊加原理。時空間隔在1PN形式下的表達式為［3，11］

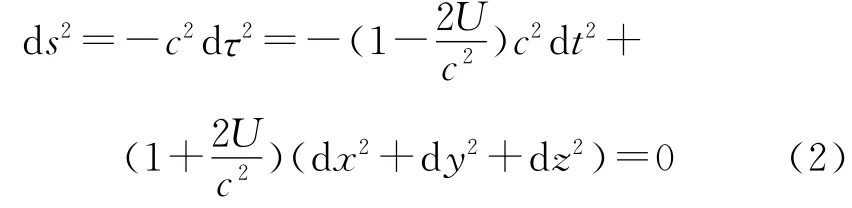
式中，c為真空光速；U為太陽系所有天體引力勢的線性疊加。由式（2）可得

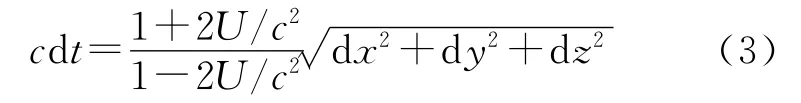
將式（3）按級數展開至O （1／c）2項，得

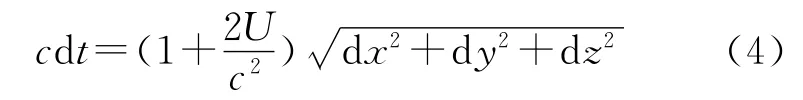
式（4）即為1PN度規形式下，時間間隔、空間間隔與天體引力勢的關系式。對此關系式沿傳播路徑積分，即可得到脈沖由脈沖星至飛行器的傳播時間。為此建立如圖1所示的坐標系，以太陽質心、脈沖星和飛行器3點所確定的平面為xy平面，取x軸平行于光線傳播方向，y、z軸按右手定則確定。其中d為太陽質心至信號傳播路徑的距離；di為太陽系內天體Mi至信號傳播路徑的距離，一般不在xy平面內；D、p分別為太陽質心至脈沖星與飛行器的矢量；＾nS、＾nSC分別為太陽質心與飛行器到脈沖星方向的單位矢量；脈沖發射時刻為tT，到達空間飛行器的時刻為tSC。在此假定光線在太陽系內傳播時，各個天體處于tSC時刻的位置，并考慮太陽引力場的彎曲效應。

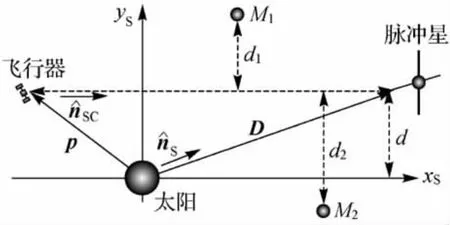
圖1 信號由脈沖星到達太陽質心與飛行器的示意圖Fig.1 The path of a signal from the pulsar to the spacecraft

在太陽引力場中，類光測地線滿足下式［1］

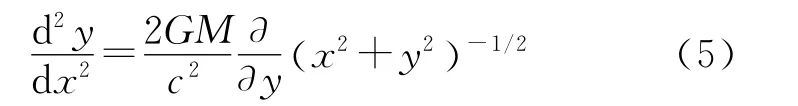
式中，GM為太陽引力常數。根據初始條件dy／dx＝0，x＝Dx，y＝d，可求得空間軌跡解為

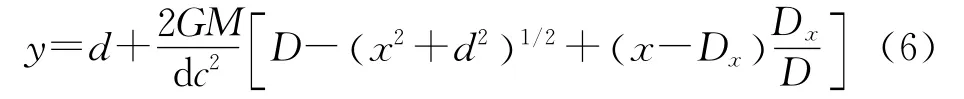
式中，D為矢量D的長度。對式（6）兩邊關于x求倒數，得

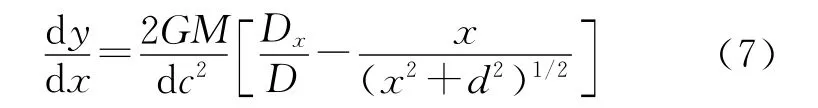
為計算信號的傳播時間，需沿信號傳播路徑積分。由于信號傳播軌跡在xy平面內，故有z＝ 0，將式（4）的空間間隔部分按級數展開，忽略O （dy2／dx2）可得

將式（7）代入到式（8），則等式右端只有唯一變量x，容易對等式兩端積分，得到信號沿路徑的傳播時間為

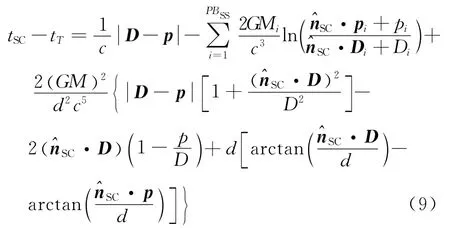
式中，PBSS為太陽系天體總數；D為脈沖到達時，脈沖星相對于太陽質心的位置；p表示飛行器接收到第N個脈沖時相對于太陽質心的位置；pi、Di為飛行器接收到脈沖時，飛行器和脈沖星相對于第i個行星的位置。式（9）即為在太陽質心坐標系中，脈沖到達飛行器的TOA表達式。若假想飛行器運動到SSB，則可用與式（9）相同的原理，得到在太陽坐標系中，脈沖到達SSB處的表達式。假定SSB在太陽質心坐標系中的位置為b，相對于第i個行星的位置為bi，SSB至脈沖星的單位矢量為，在式（9）中，以b代p、以bi代pi、以代，即可得到SSB處的TOA表達式。在推導出飛行器的TOA與太陽系質心的TOA方程之后，將兩式求差即可得到導航觀測方程。具體形式為

式中，dSSB為信號到達SSB時，太陽質心至信號傳播路徑的距離；dSC為信號到達飛行器時，太陽質心至信號傳播路徑的距離。以下將利用數值計算方法，對觀測方程精度進行分析。

3 觀測方程的精度分析

為分析脈沖星導航觀測方程的精度，給定以下計算條件：① 模擬繞地飛行器的軌道根數見表1；②3顆脈沖星的參數信息見表2；③太陽系內各個天體的位置由JPL行星星歷給出；④計算的起始歷元為2010－01－01（55 197.0MJD），時間跨度1000d。

表1 飛行器軌道根數Tab.1 Orbit elements of the spacecraft

表2 X射線源的參數值［3，6－7］Tab.2 Parameters of X－ray sources［3，6－7］

3.1 相對論影響分析

在表達式（10）中，脈沖星導航的相對論效應由兩部分組成：一是太陽系天體的引力時延（第3、4項）；二是太陽引力彎曲時延（第5、6項）。這兩部分時延對脈沖星觀測時間的影響分別如圖2、圖3所示。

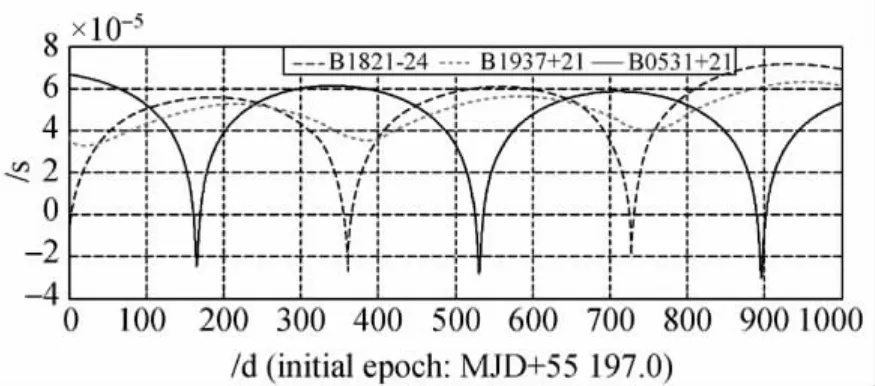
圖2 太陽系天體的引力時延Fig.2 Time delay of the gravity by bodies of the solar system

從圖2中可看出，由于脈沖星位置不同，脈沖信號所受引力時延的影響不同。但均呈現周年變化，這是由地球公轉所致。考慮到太陽繞SSB的公轉，引力時延還應有一個約為12a的變化周期。圖3是太陽引力彎曲導致的時間延遲，其量級小于1ns，在目前脈沖星觀測精度下可忽略。

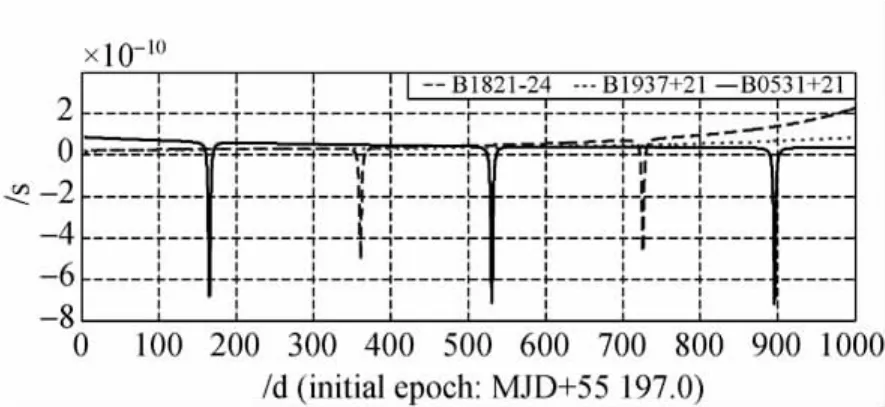
圖3 太陽引力彎曲Fig.3 Time delay of the path bending by the Sun

3.2 脈沖星星表誤差的影響

脈沖星歷表是脈沖星導航的基礎，其誤差對脈沖星導航性能具有重要影響。為推導脈沖星星表參數誤差與觀測時間之間的關系式，忽略式（10）中的引力彎曲效應，將真空光行時部分按級數展開至二階。由于脈沖星距離遙遠，可近似認為脈沖星相對于SSB和飛行器的方向相同，即有，由此可得表達式

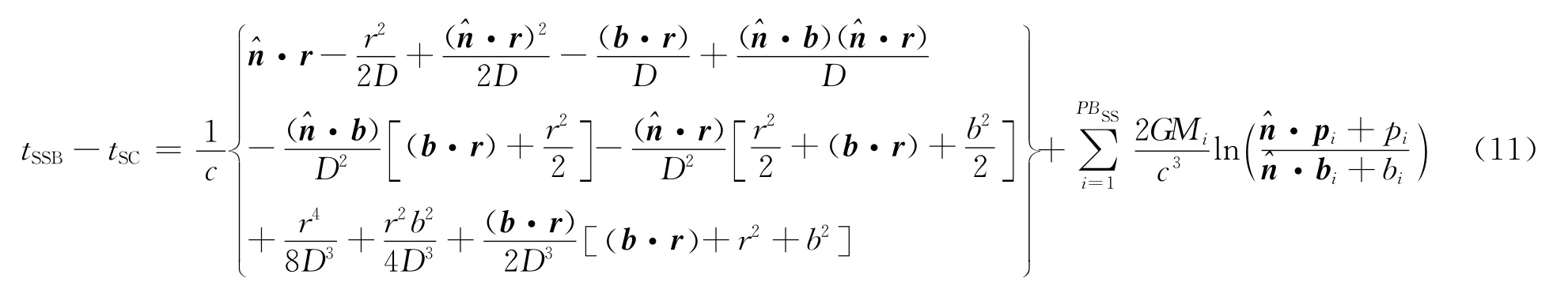
由式（11）可求觀測時間對脈沖星位置（赤經、赤緯）與距離的偏微分，得到以下表達式

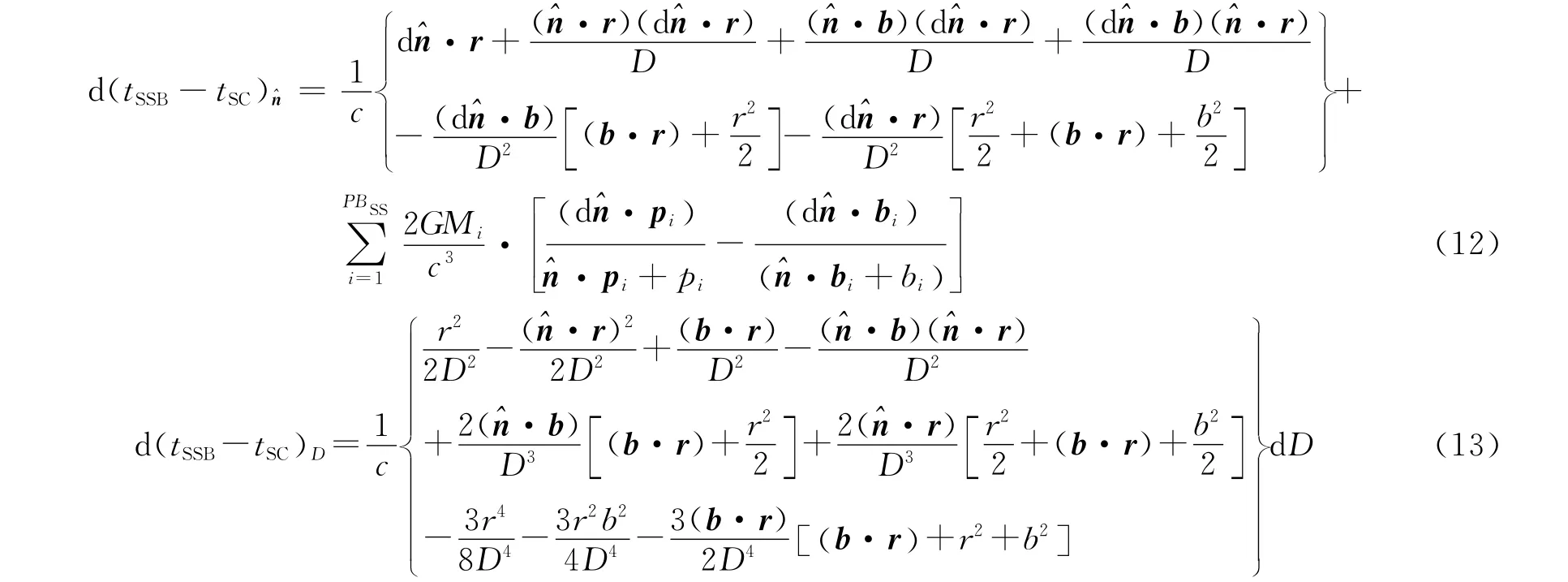
式中

假定脈沖星距離的系統偏差為距離值的10%，位置的系統偏差為0.001″，可得到在不同時刻，它們對觀測時間的影響，如圖4、圖5所示。

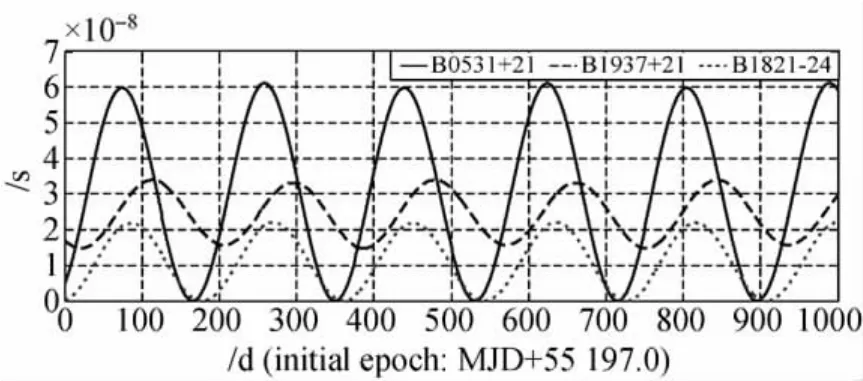
圖4 脈沖星距離偏差對觀測時間的影響Fig.4 Timing error due to the distance deviation of pulsar

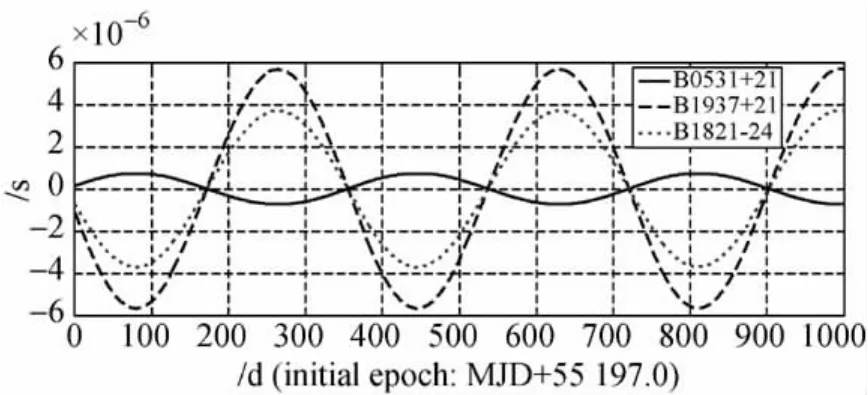
圖5 脈沖星位置偏差對觀測時間的影響Fig.5 Timing error due to the direction derivation of pulsar

由圖5、圖6可以看出，不同脈沖星距離和位置的偏差引起的測量誤差均呈現相同的周期性，周期為半年，但幅值不同。距離偏差對觀測時間的影響相對較小，且與脈沖星的距離成反比；而位置系統偏差對觀測時間的影響較大，0.001″的偏差對觀測精度的影響可達數微秒，且與脈沖星位置有關。

假定脈沖星距離的隨機誤差均值為0，均方差為距離值的5%，位置的隨機誤差均值為0，均方差為0.000 5″，對于不同的脈沖星，參數的隨機誤差對觀測時間的影響如圖6、圖7所示。

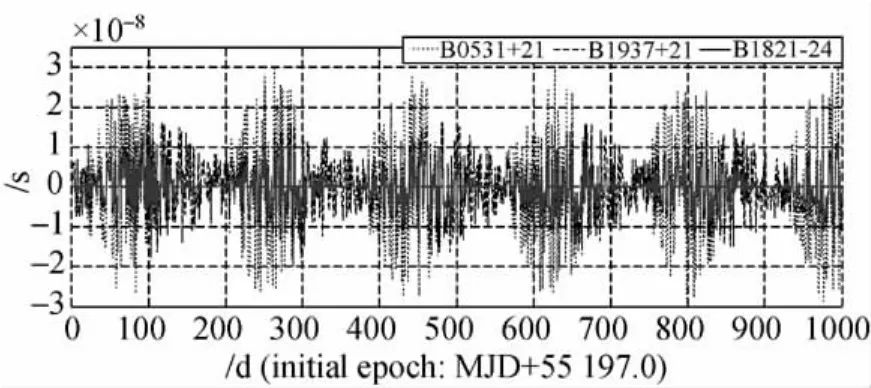
圖6 脈沖星距離的隨機誤差對觀測時間的影響Fig.6 Timing error due to the random error of pulsar distance

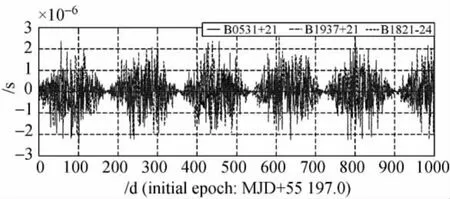
圖7 脈沖星位置的隨機誤差對觀測時間的影響Fig.7 Timing error due to the random error of pulsar position

圖6中脈沖星距離的隨機誤差引起的測量誤差在±30ns之間；圖7中脈沖星位置隨機誤差引起的測量誤差在±3μs之間。當前脈沖星歷表的位置參數精度大多低于0.001″，可見脈沖星位置參數的精化是提高時間測量精度的關鍵。

3.3 行星星歷誤差的影響

JPL行星星歷在天文精密觀測的分析與歸算、引力定律檢驗、行星探測計劃、衛星導航以及深空導航中得到廣泛應用。其不同版本根據不同需求而制定，在精度有差異。為分析不同行星歷表之間的差異，以下選擇DE200、DE403、DE405以及DE423進行比較，對于地球在太陽系質心坐標系中的三維位置而言，不同星歷在相同歷元的差值如圖8所示。

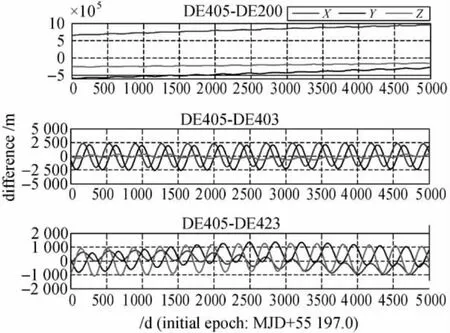
圖8 地球的太陽系質心位置之差Fig.8 Difference in position of the geocenter in the barycentric system

由圖8可見，DE200與DE405的坐標差異最大，可達數十千米，且有一定的系統性。DE403與DE405之間的差異主要表現在x、y方向，z方向的互差較小，且呈周年變化；而DE423與DE405之間的差異更小，最大差值約1km，也呈現周年變化，這說明DE系列的后續歷表逐步精化。為分析歷表差異對時間測量的影響，以表3中的3顆脈沖星為例，分析不同行星星歷在相同歷元，對飛行器觀測時間的差值如圖9所示。

由圖9可見，DE200與DE405的差值可達毫秒量級；DE423與DE405的差值較小，對于Crab和B1821－24脈沖星，變化范圍為±2μs；對于B1937＋21脈沖星，變化范圍為±4μs。可見行星星歷的精化對觀測精度的提高具有重要意義。

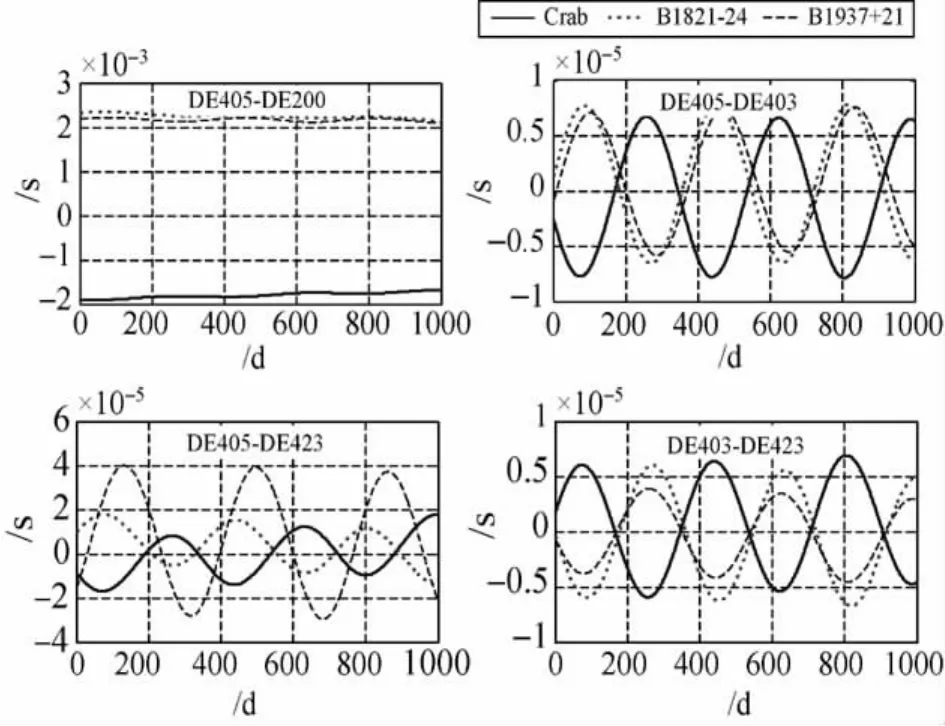
圖9 不同行星星歷引起的時間差Fig.9 Timing difference due to the different planet ephemeris

3.4 星體扁率的影響

在脈沖星導航觀測方程中，通常將星體作為質點或均質球體近似處理。對于有些星體，如木星，其質量大、自轉快，實際形狀更接近于兩極略扁的球體，因此，有必要討論其非球形的引力攝動對觀測時間的影響。由引力理論可知，顧及扁率的星體外部點的引力位為可表為［18］

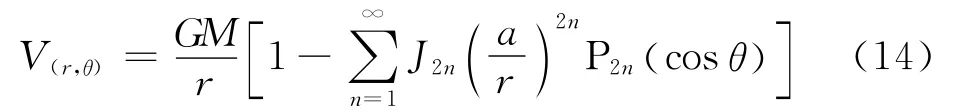
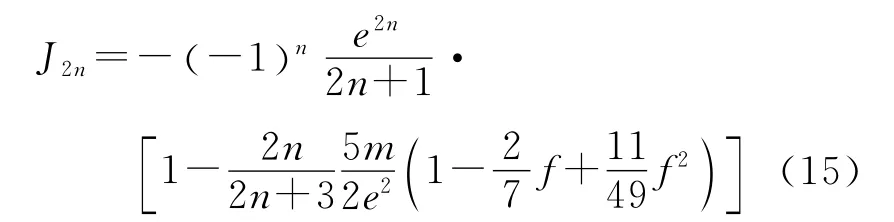
式中，m＝4π2a3（1－f ）／T2GM；f為扁率，e＝為橢球第一偏心率。由星體扁率引起的引力位的改正位可表為

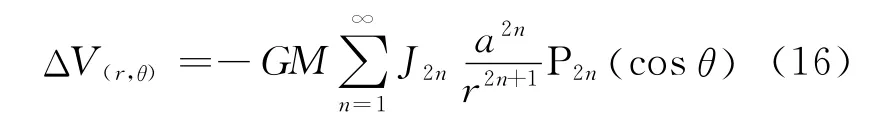
該改正位對觀測時間的延遲影響為

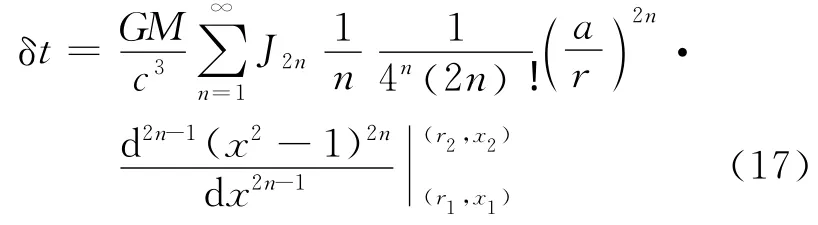
式中，x1＝cosθ1；x2＝cosθ2；θ1、θ2為外部點到星體自轉軸之間的極距。由于星體自轉平面與公轉平面一般不同，除地球外，其他星體的公轉平面對自轉平面的升交點位置未知，故外部點相對于星體自轉軸的極距難以得到。如只對改正位的時延量級作分析，可由以下方法進行評估。

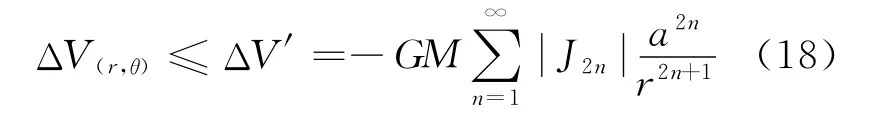
可得由星體扁率引起的時延δt滿足

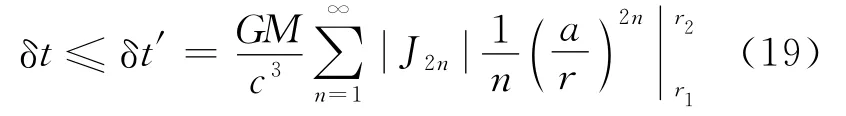
根據式（19）即可對改正位的時延作量級分析。若考慮太陽系天體的基本參數如表3所示，根據式（15）可計算得到各星體的帶諧項系數。

表3 各星體的基本參數［19－20］Tab.3 Parameter of each celestial body［19－20］

在式（19）中，取n＝3，可得在不同時刻，星體的扁率對觀測時間的影響，見圖10。由圖10可見，太陽扁率對繞地飛行器觀測時間的影響最大，但其最大量級也只有10－12s，導航中可忽略。

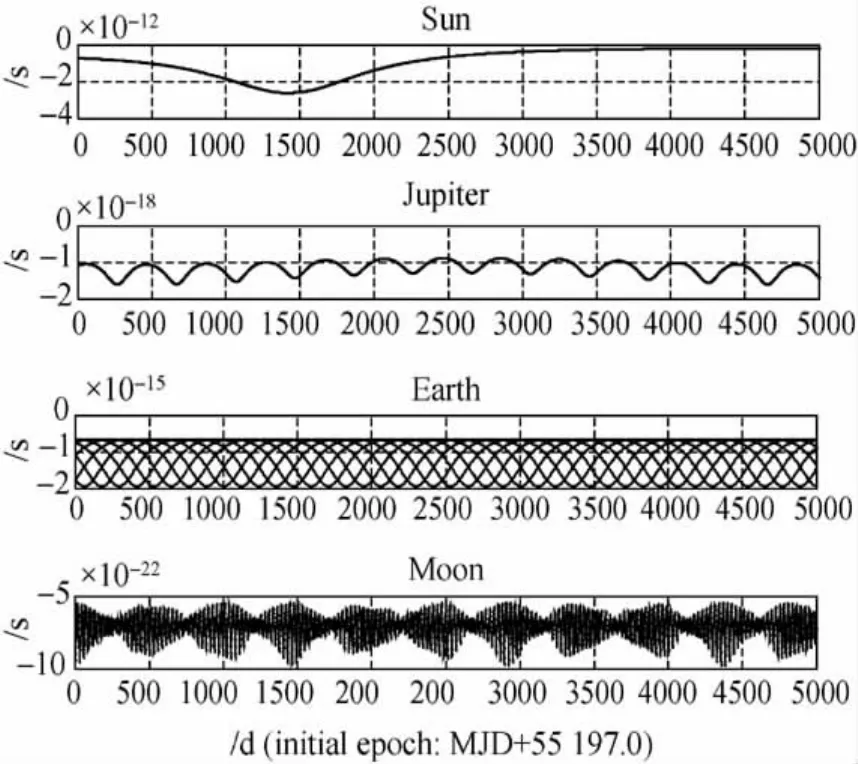
圖10 顧及各星體扁率對信號傳播路徑的時延修正Fig.10 Time correction of transmitting path by the flattening of bodies

4 結 論

本文綜合相關研究成果，完整推導了1PN形式下脈沖到達時間轉換方程。分析了脈沖星觀測方程中的相對論效應；獨立推導了觀測時間誤差與脈沖星歷表誤差之間的解析關系式和顧及星體扁率的觀測時間延遲表達式；分析了脈沖星距離誤差、位置誤差對觀測時間的影響；比較了不同行星星歷之間的差異，分析了這些差異對脈沖星觀測的影響；分析了星體扁率對觀測時間的延遲量級。主要結論有：

（1）太陽系天體對信號傳播路徑的引力時延可達幾十微秒，在精確的觀測方程中需要考慮；太陽對信號傳播路徑的彎曲所引起的時延較小（＜1ns），在當前的測量精度下可不考慮。

（2）脈沖星位置誤差對時間方程的影響較大，距離誤差影響相對較小，在當前情況下，通過長期觀測，逐步精化脈沖星歷表，尤其是位置參數，是提高觀測精度的有效途徑之一。

（3）行星星歷誤差可引起數微秒的觀測時間誤差，且對不同脈沖星影響不同。

（4）星體扁率對觀測時間的延遲很小，在近地飛行器自主導航中可忽略。

［1］ HELLING R W.Relativistic Effects in Astronomical Timing Measurement［J］.The Astronomical Journal，1986，91（3）：650－659.

［2］ BACKER D C，HELLING R W.Pulsar Timing and General Relativity［J］.Annual Review of Astronomy and Astrophysics，1986，24：537－575.

［3］ SHEIHK S I.The Use of Variable Celestial X－Ray Sources for Spacecraft Navigation［D］.Baltimore：University of Maryland，2005.

［4］ SHEIHK S I，HELLINGS R W，MATZNER R A.Highorder Pulsar Timing For Navigation［C］∥Proceedings of the 63rd Annual Meeting of the Institute of Navigation，Cambridge：ION，2007：432－443.

［5］ GRAVEN P H，COLLINS J T，SHEIKH S I，et al.Spacecraft Navigation Using X－ray Pulsar［R］.County Kerry：7th International ESA Conference on Guidance，Navigation ＆Control Systems，2008.

［6］ SHEIHK S I，PINES D J，RAY P S，et al.Spacecraft Navigation Using X－ray Pulsar［J］.Journal of Guidance，Control，and Dynamics.2006，29（1）：49－63.

［7］ RAY P S，SHEIHK S I，GRAVEN P H，et al.Deep Space Navigation Using Celestial X－Ray Sources［C］∥Proceedings of the 2008National Technical Meeting of the Institute of Navigation.San Diego：ION，2008：101－109.

［8］ BACKER D C：Millisecond Pulsars［J］.J Astrophys Astr，1984（5）：187－207.

［9］ KASPI V M，TAYLOR J H，RYBA M F.High－precision Timing of Millisecond Pulsar.III.Long－term Monitoring of PSRs B1885＋09and B1937＋21［J］.The Astrophysical Journal，1994，428（2）：713－728.

［10］ HUANG Zhen，LI Ming，SHUAI Ping.On Time Transfer in X－Ray Pulsar Navigation［J］.Science in China：Series E，Technological Sciences，2009，52（5）：1413－1419.

［11］ MCCARTHY D D，PETIT G.IERS Technical Note：No.32［M］.Frankfurt：IERS，2004：14－86.

［12］ SALE J，URRUELA A，VILLARES X，et al.Feasibility Study for a Spacecraft Navigaiton System Relying on Pulsar Timing Information［R］.［s.L.］：ESA，2004.

［13］ LORIMER D R，KRAMER M.Handbook of Pulsar Astronomy［M］.Cambridge：Cambridge University Press，2005.

［14］ ZHAO Ming，HUANG Tianyi.An Astrometry Parsing to the Data of Pulsar Timing［J］.Science in China：Series G，2009，39（11）：1671－1677.（趙敏，黃天衣.脈沖星計時數據的天體測量解析［J］.中國科學：G輯，2009，39（11）：1671－1677.）

［15］ FEI Baojun.Application of Relativity in Modern Navigation［M］.Beijing：National Defense Industry Press，2007.（費保俊.相對論在現代導航中的應用［M］.北京：國防工業出版社，2007.）

［16］ MAO Yue.Research on X－Ray Pulsar Navigation Algorithms［D］.Zhengzhou：Information Engineering University，2009.（毛悅.X射線脈沖星導航算法研究［D］.鄭州：信息工程大學，2009.）

［17］ FEI Baojun，PAN Gaotian，YAO Guozheng，et al.Arithmetic of Frequency Drift and Time Delay between Pulse Profiles in XNAV［J］.Acta Geodaetica et Cartographica Sinica，2011，40（Sup）：126－132.（費保俊，潘高田，姚國政，等.X射線脈沖星導航中脈沖輪廓的頻偏和時延算法［J］.測繪學報，2011，40（增刊）：126－132.）

［18］ LU Zhonglian.Theory and Method of Earth’s Gravity Field［M］.Beijing：Liberation Army Press，1996.（陸仲連.地球重力場理論與方法［M］.北京：解放軍出版社，1996.）

［19］ LIU Xuefu.Fundamental Astronomy［M］.Beijing：Higher Eduation Press，2004.（劉學富.基礎天文學［M］.北京：高等教育出版社，2004.）

［20］ OHANIAN H C，RUFFINI R.Gravity and Spacetime［M］.Beijing：Science Press，2006.（OHANIAN H C，RUFFINI R.引力與時空［M］.北京：科學出版社，2006.）