基于LMS算法與RLS算法的自適應濾波

徐艷，李靜

（長安大學 信息工程學院，陜西 西安 710064）

隨著數字信號處理器性能的增強，自適應濾波器的應用也越來越常見，它主要應用于系統辨識、回波消除、自適應譜線增強、自適應信道均衡、語音現行預測、自適應天線陣等諸多領域中。自適應濾波器是根據環境的改變，使用自適應算法來改變濾波器的參數和結構。自適應濾波器算法決定了濾波的性能，根據濾波算法優化準則不同，自適應濾波器算法可分為兩類基本算法：最小均方誤差（LMS）算法和遞歸最小二乘（RLS）算法。

1 自適應濾波器的原理

自適應濾波就是利用前一時刻獲得濾波器參數的結果自動的調節現時刻的濾波器參數，以適應信號和噪聲未知的或隨時間變化的統計特性，從而實現最優濾波。自適應濾波器實質上就是一種能調節其自身傳輸特性以達到最優的維納濾波器。自適應濾波器的特性變化是由自適應算法通過調整濾波器系數來實現的。一般而言，自適應濾波器由參數可調的數字濾波器和自適應算法兩部分組成。參數可調數字濾波器可以是FIR數字濾波器或IIR數字濾波器，也可以是格型數字濾波器。自適應濾波器的一般結構如圖1所示[5-6]。

圖1中x（n）為輸入信號，通過參數可調的數字濾波器后產生輸出信號y（n），將輸出信號y（n）與期望信號d（n）進行比較，得到誤差信號e（n）。e（n）和x（n）通過自適應算法對濾波器的參數進行調整，調整的目的使得誤差信號e（n）最小。

自適應濾波器大多用FIR來實現。直接型自適應濾波器FIR濾波器如圖2所示。

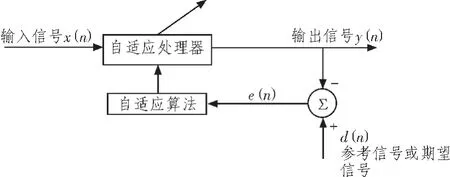
圖1 自適應濾波器的一般結構Fig.1 General structure of adaptive filter

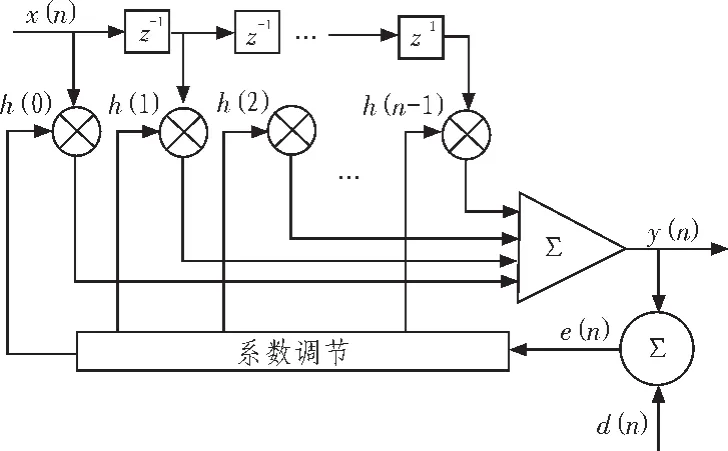
圖2 直接型自適應濾波器FIR濾波器Fig.2 Direct type adaptive filter FIR filter

2 自適應濾波算法

自適應濾波器的算法主要是以各種判據條件作為推算基礎的。通常有兩種判據條件：最小均方誤差判據和最小二乘法判據。即自適應濾波有兩類基本的算法：最小均方誤差（LMS）算法和遞歸最小二乘（RLS）算法[1]。

1）最小均方誤差（Least Mean Square，LMS）算法

最小均方誤差（Least Mean Square，LMS）算法是一種易于實現、性能穩定、應用廣泛的算法。LMS算法設法使y（n）接近d（n），理想信號 d（n）與濾波器輸出 y（n）之差 e（n）的期望值最小，并且根據這個判據來修改權系數wi（n）。均方誤差ε表示為：

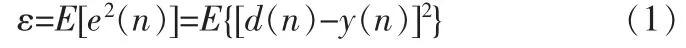
對于橫向結構的濾波器，代入y（n）的表達式：

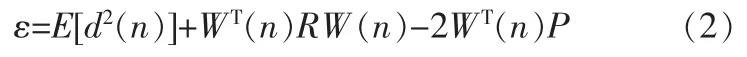
其中：R=E[X（n）XT（n）]為 N×N 的自相關矩陣，它是輸入信號采樣值間的相關性矩陣。P=E[d（n）X（n）]為 N×1 互相關矢量，代表理想信號d（n）與輸入矢量的相關性。在均方誤差ε 達到最小時，得到最佳權系數 W*=[ω*0，ω*1，…，ω*N－1]T它應滿足下式:

求解最佳權系數W*的兩種方法，一種是最陡梯度法。其思路為：設計初始權系數W（0），用W（n+1）=W（n）－uΔ（n）迭代公式計算，到W（n+1）與W（n）誤差小于規定范圍。其中Δ（n）的E[]計算可用估計值表達式為：

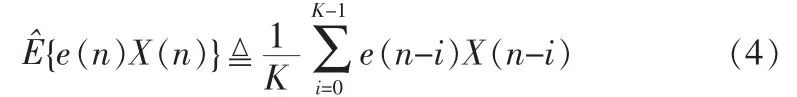
上式K取值應足夠大。如果用瞬時－2e（n）X（n）來代替上面對－2E{e（n）X（n）}的估計運算，就產生了另一種算法——隨機梯度法，此時迭代公式為：

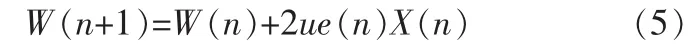
LMS算法基本上是一種遞推算法，它用任意選擇的{h（k）}的初始值作為開始，然后將每一新的輸入樣本{x（n）}輸入到這個自適應FIR濾波器，計算相應的輸出{y（n）}，形成誤差信號 e（n）=d（n）－y（n）并按方程 hn（n）=hn－1（k）+Δe（n）x（n－k），0≤k≤N－1更新濾波器系數，這里Δ稱為步長參數，x（n－k）是輸入信號在時間n位于濾波器的第k個樣本，而e（n）x（n－k）是對第k個濾波器系數的一個梯度負值的近似估計[2]。

2）遞歸最小二乘（Recursive Least Square，RLS）算法

遞歸最小二乘（Recursive Least Square，RLS）算法是在最小均方誤差算法的基礎上得來的。所不同的是在求均方誤差時觀測數據的長度是變化的，且隨著觀測數據的時間先后順序分別乘了加權因子。即RLS算法的均方誤差變成:

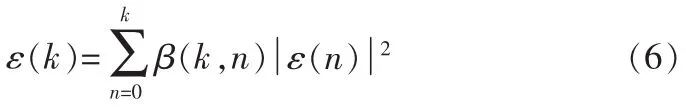
式中：β（k，n）是加權因子，滿足:0＜β（k，n）≤1，n=1，2，…，k。這樣會使很多次迭代之前的數據被遺忘掉，當濾波器工作在非平穩環境中時，觀測數據仍可能服從統計變化的一些特性。其中遺忘因子的最常用形式為指數加權因子，即:

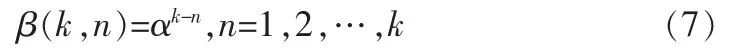
式中:α是一個接近1但小于1的數。將式（7）代入式（6）可以得到均方誤差的具體表達式為:

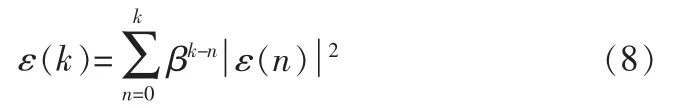
當ε（k）達到最小值時，有下列關系:

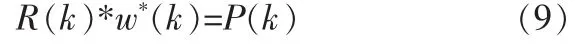
w*（k）為均方誤差達到最小時的自適應濾波器最佳權系數。由式（9）可知，要求出w*（k）需要先確定。為此我們把R－1（k）當前的瞬時估計分離出來:

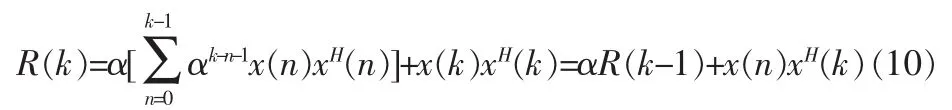
對于p（k）做同樣的處理可以得到:

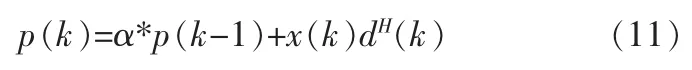
由矩陣求逆定理:若A和B是2個M×M的正定矩陣，存在關系:A=B+C*D－1*CH，其中C是一個 M×N矩陣，D是一個N×N 正定矩陣，則有 A=B－B*C（D+CH*B*C）－1。可以令 A=R（k），B=α*R（k－1），C=（k），D=1 代入上面的矩陣逆定理公式可得:

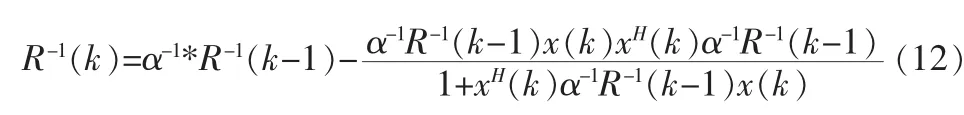
如果記:

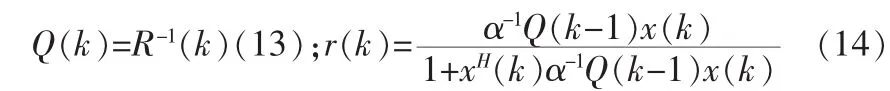
則式（12）變形如下:

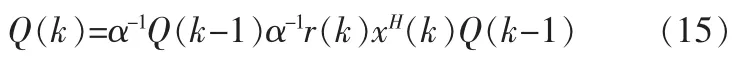
把式（15）反代入式（14）可以得到以下的關系:r（k）=R－1（k）x（k）

由式（9）得到計算權向量的公式為:

將式（15）代入式（16）右端第一項可以得到：w（k）=w（k－1）+r（k）·η（k）。

式中:η（k）=d（k）－wH（k－1）x（k）。這樣就得到了權向量迭代的計算公式。

總結以上推導步驟歸納出RLS算法實現流程如下:

3 MATLAB仿真實驗

1）LMS算法的自適應濾波部分實現程序代碼如下：

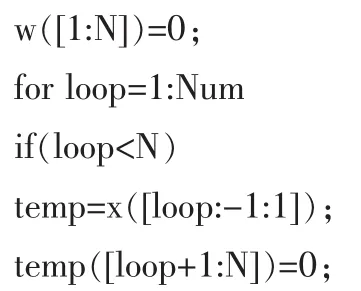
仿真結果：

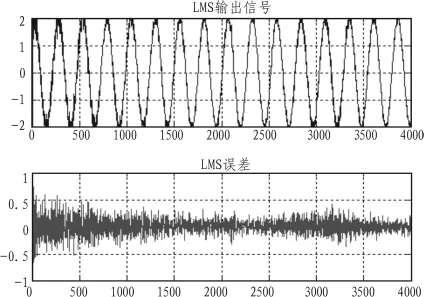
圖3 LMS算法的自適應濾波仿真結果Fig.3 LMS algorithm of adaptive filter simulation results

2）RLS算法的自適應濾波部分實現程序代碼如下：

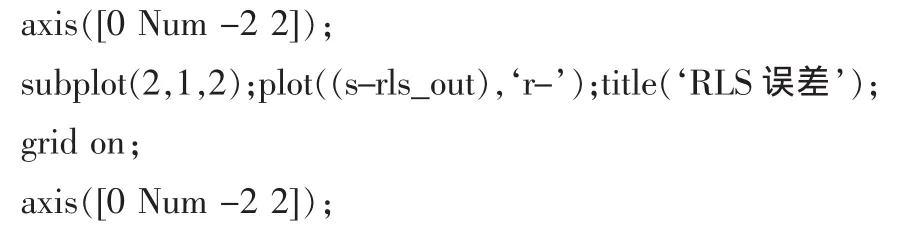
仿真結果：

圖4 RLS算法的自適應濾波仿真結果Fig.4 LMS algorithm of adaptive filter simulation results

4 結 論

LMS算法易于實現、性能穩定、應用廣泛，但LMS算法對非平穩信號的適應性差且收斂速度慢。RLS算法具有較好的收斂性能和跟蹤能力，收斂速度快于LMS算法以及穩定性強，具有更小的權噪聲和更大的抑噪能力，但是他的計算量很大。目前最快的RLS算法要比LMS算法多2～3倍的計算量。

LMS與RLS都是來一個數據輸出一個數據，階數和濾波系數可變，易于調整，是實際應用的實現方法。LMS的效果和步長因子μ的選取有很大關系，一般濾波器階數越大，它的值取得越小，RLS濾波效果和λ有關，其濾波輸出的信號比LMS要好一些，但運算量很大，基本是N2的數量級，而LMS運算量是 O（N）。

[1]石艷麗，譚忠吉，于海霞.基于LMS算法自適應噪聲抵消系統的仿真研究[J].電子測量技術，2009（6）:71－74.SHI Yan-li，TAN Zhong-ji，YU Hai-xia.LMS algorithm based on adaptive noisecan cellation of the simulation system[J].Electronic Measurement Technology，2009（6）:71－74.

[2]嚴雪艷，郭建中.基于LMS自適應濾波器對噪聲干擾的語音恢復研究[J].陜西師范大學學報，2009（3）:25－28.YAN Xue-yan，GUO Jian-zhong，Based on adaptive LMS noise filter to restore the speech[J].Shanxi Normal University Press，2009（3）:25－28.

[3]衡霞，劉志鏡.基于自適應濾波的語音增強和噪聲消除[J].微機發展，2004（1）:33－35.HENG Xia，LIU Zhi-jing.Based on adaptive filter speech enhancement and noise elimination[J].Microcomputer Development，2004（1）:33－35.

[4]張賢達.現代信號處理[M].2版.北京:清華大學出版社，2002.

[5]龔耀寰.自適應濾波器[M].北京:電子工業出版社，1989.

[6]Simon Haykin，鄭寶玉，等譯.自適應濾波器原理[M].北京:電子工業出版社，2006.

[7]李正周.MATLAB數字信號處理與應用[M].北京:清華大學出版社，2008.

[8]羅軍輝，等.《Matlab7.0在數字信號處理中的應用》[M].北京：機械工業出版社，2005.