基于雙線性內插的圖像處理算法及其優化

曹亞君，邵玉蘭

(商丘職業技術學院計算機系，河南商丘476000)

數字圖像處理是指用計算機對圖像經過采樣和數字化后的二維數組進行分析處理，以達到所需結果的技術，圖像處理所涉及的應用領域也包括了人們工作、學習和生活中的各個方面。在圖像處理技術中最常見的就是圖像放大，也就是將一幅低分辨率的圖像獲得它的高分辨率版本的一種圖像處理技術。在航天航空、生物醫學工程、通信工程以及工業生產等各方面有著非常廣泛的應用。

1．數字圖像處理中的插值算法

插值算法是一種應用十分廣泛的方法。在數學表示法中，通常用y=f(x)表示一條平面曲線(若是二維函數則為曲面)，為了代替原來的函數y=f(x)中的數據，就需要找到另一個函數φ=f(x)，找尋這個替代的函數即為插值。圖像插值就是利用已知鄰近像素點的灰度值來產生未知像素點的灰度值，以便由原始圖像再生出具有更高分辨率的圖像。［1］插值算法會自動選擇信息較好的像素作為增加的像素，而并非只使用臨近的像素，所以在放大圖像時，圖像看上去會比較平滑、干凈。插值是數字圖像處理領域里一個很大的分支，對于增加的未知像素采用哪一種插值方式是圖像放大算法的關鍵。常用的插值算法有最鄰近插值算法(Nearest Neighbor interpolation)、雙線性內插算法(Bilinear interpolation)和雙立方插值算法(Bicubic interpolation)。

最鄰近插值算法是最簡單的一種插值算法，當圖片放大時，缺少的像素通過直接使用與之最接近的原有的像素的顏色生成，也就是把原始像素直接復至到其領域內。它是三種內插值方式中質量最差的一種，放大后的圖像會出現明顯的鋸齒或方塊，效果比較模糊，比較適合于放大倍數較小且對質量要求不高的場合。［2］

雙線性內插算法是沿X軸方向和Y軸方向分別對未知像素點進行一次線性插值取樣，然后求得加權平均值，即為該點像素的顏色值。這種算法極大地消除了鋸齒現象，放大后的圖像平滑性好，但會使圖像邊緣模糊，在計算速度與質量兩個方面都居于三種方法中間地位。雙立方插值算法是在沿X軸、Y軸和對角線Z軸方向對未知像素點取樣，求得該點鄰近的16個像素點值，依據對其遠近影響進行插值計算，得到該點像素的顏色平均值。雖然雙立方插值算法可以得到最佳畫質，但是它的計算復雜度實在太大了，即使采用了整數優化和查表法，也將耗去大量的CPU資源，不太實用。本文主要討論在數字圖像的實時處理中，用途最廣的雙線性內插算法及其優化。

2．雙線性內插圖像放大算法及優化

2．1．雙線性內插算法原理

雙線性內插，又稱雙線性插值法。用數學表示法來表示，雙線性內插是插值函數的一種具有兩個變量的線性插值擴展，其主要原理是對未知像素點鄰近的四個像素點在X軸和Y軸方向進行線性插值。雙線性插值和最近鄰點插值法相比，可以產生一個能保持連續性和連通性的光滑映射，產生更令人滿意的效果。［3］將高為strH、srcW的圖像插值為高和寬分別為desH、desW的插值圖像，插值前后圖像的坐標分別用(x，y)和(i，j)來表示。則此圖像插值后圖像中任一點的像素值可由插值前圖像中坐標為(x，y)，(x+1，y)，(x，y+1)和(x+1，y+1)所對應的4個像素的值確定。［4］如圖1所示，即

式中:u，t分別為插值點坐標(i，j)與坐標(x，y)在x和y方向的浮點距離，且0≤t＜1，0≤u＜1，由下列計算得到

對上述計算過程類推，可計算得插值圖像中其他各點的像素值。

圖1 目標圖像像素灰度值的確定

2．2．基于邊緣的內插值優化算法

雙線性內插算法使放大后的圖像平滑性好，較好地消除了鋸齒現象，但其具有低通濾波性質，該方法會使高頻分量受損，圖像輪廓有一定模糊。因此為了減少雙線性內插算法使圖像邊緣模糊的問題，對其算法優化，主要是進行銳化處理，使圖像視覺效果更好，圖像輪廓得到加強。

首先使用雙線性內插值對原始圖像進行放大，然后將放大后的圖像使用高通濾波讓高頻分量通過，使圖像的邊緣或線條等細節變得清晰，實現圖像銳化。為了達到圖像實時處理的需要，因此使用線性的FIR濾波器對圖像邊緣處理。［5］

其中w(x，y)為高通濾波算子的系數，p(x，y)為中心點的像素值。

在YUV數據格式中，以圖像前兩行像素處理的數據為例，原始圖像第一行和第二行的128個Y分量數據如下表1所示。

表1 原圖像Y分量數據

對原始圖像使用雙線性內插算法放大2倍后，由每行的128個數據插值可得到兩行256個Y分量數據，如下表2所示。放大后的UV數據分量也通過此插值計算得到。

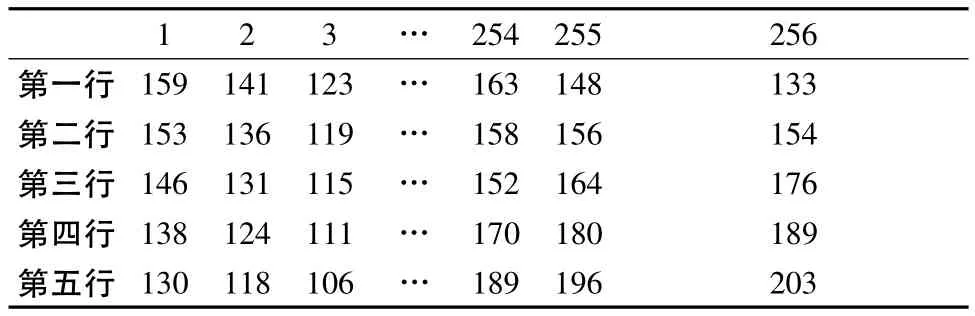
表2 放大后圖像Y分量數據

在對原始圖像插值放大后，接著用線性的FIR高通濾波器銳化。由于這種FIR濾波器必須滿足濾波器的中心系數為正數，其他系數為負數，故這里使用線性高通濾波器3×3模板的典型系數，如式(2)所示。將放大后圖像的Y分量數據進行兩次緩存處理，就得到了一個的窗口，每個像素點的系數如式(2)所示。

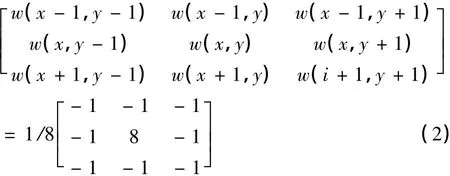
3．實驗結果與分析

首先將原始256×256的灰度Lena圖像降采樣到128×128圖像，結著再分別應用雙線性內插算法及其優化算法對圖像再進行放大處理，對比分析還原之后的效果。如圖2所示，其中(a)為降采樣后的128×128圖像，(b)為應用雙線性內插算法的結果，圖像較平滑，但邊緣輪廓有一定模糊，(c)為應用邊緣增強處理優化算法的結果，與圖(b)相比，圖像的邊緣輪廓較清晰，如眼部、帽沿等邊緣部分，使處理后的圖像效果更好。

圖2 插值算法效果對比圖

4．結束語

在數字圖像的實時處理中，放大圖像是一種常用技術。考慮到運算速度、硬件等條件，采用雙線性內插是最實用的一種算法。因放大后的目標像素值是其4個鄰近像素的加權平均值，具有低通濾波的性質，高頻分量受損，所產生的圖像邊緣會有一定的模糊，故本文對雙線性內插放大圖像算法進行優化處理。加強了圖像邊緣的銳化，采用高通濾波器使圖像的高頻分量信息得以通過，提高了邊緣細節的清晰度。因此，優化的雙線性內插算法在圖像的實時放大中具有更好的效果。

［1］符祥，郭寶龍．圖像插值技術綜述［J］．計算機工程與設計，2009，30(1):141 －144．

［2］劉麗君，駱婷．插值法在圖像處理中的應用［J］．硅谷，2009(9):9－10．

［3］陳寶平，趙俊崗，尹志凌．雙線性插值算法的一種快速實現方式［J］．北京電子科技學院學報，2004，12(4):21 －23．

［4］［美］岡薩雷斯．數字圖像處理［M］．阮秋奇，阮宇智，譯．北京:電子工業出版社，2005:9．

［5］戴玉良．用DSP實現FIR數字濾波器［J］．臺州學院學報，2006，28(6):43 －46．