基于KMV模型的上市公司信用風險評價
湖北科技學院 方軍武
目前,我國的上市公司信用風險管理還相對薄弱,相關理論和實踐還比較缺乏,基本上是引進和借鑒國外較為成熟的信用評估理論和方法,如KMV模型、Creditmetrics模型、麥肯錫模型等。盡管每種模型都各有特點,而且適用的前提和條件也各不相同,但KMV模型由于以現代期權理論為基礎,主要從上市公司股票市場價格的變化來分析其信用風險,更能反映上市企業當前的信用狀況,具有較強的前瞻性和客觀性。本文在對KMV 模型的求解過程進行深刻分析的基礎上,以2009年的ST公司為樣本,用其對我國上市公司的信用風險進行識別和評價。
一、KMV模型的研究方法及參數設計
(一)K M V 模型評估公司信用風險的基本原理 首先,建立上市公司股權價值與資產價值的估計模型,通過公司股權、負債的價值以及波動率等變量估計公司資產的市場價值及波動率;其次,以公司一年以內短期負債加上公司長期負債的一半來計算公司的違約實施點(DP);最后,公司資產價值的期望值(V)減去違約實施點則表示該公司的違約距離(DD),違約距離(DD)數值越大,則表示公司距離違約的可能性越小,反之違約距離(DD)數值越小,則表示公司距違約實施點越近,公司違約的可能性越大。違約距離(DD)在公式上等于公司總資產公允價值標準差的倍數。由于違約實施點(DP)等于公司流動負債加上長期負債的一半,那么違約實施點(DP)通常大于公司的流動負債而小于公司的負債總額。對違約概率(EDF)的度量分三步進行:首先,根據歷史數據建立模型估計公司總資產的市場價值及波動率;隨后,建立模型估計公司的違約距離DD(Distance-to-Default),違約距離(DD)的大小反映了公司違約可能性的大小,是公司還貸風險的一種指標顯示;最后,對違約距離(DD)的估計模型進行T統計檢驗,得出相應上市公司的信用風險情況。
(二)K M V 模型的內容 主要包括:
(1)計算資產價值及其波動性。根據Black-Scholes的期權定價公式,可以得到以下的表達式:
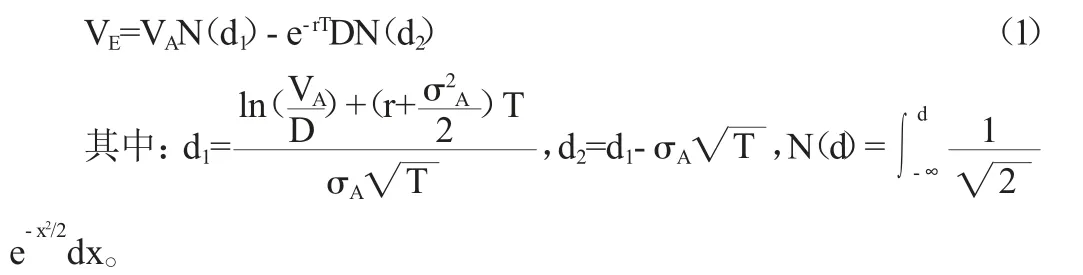
其中:VE為公司股票的市值總額,VA為公司總資產公允的市場價值,D為公司銀行負債的賬面價值,r為無風險收益率(同期限國債收益率),T為銀行負債的剩余期限,N為標準累積正態分布函數,σA為公司總資產價值的波動率,σE為公司股票總市值的波動率。
由于公司總資產公允的市場價值VA與波動率σA是未知變量,無法從單個的Black-Scholes期權定價模型中求解,而上市公司的股權價值往往可以獲得,因此需要建立公司總資產市場價值及波動率與公司股權價值及波動率之間的數學關系,然后聯立Black-Scholes期權定價模型與公司資產價值模型兩個模型來求解。
先對(1)式兩邊同時求導數,然后求期望,整理可得:

這樣利用Matlab統計計算軟件來計算包含上述兩個模型的聯立方程組,就可以求得公司總資產的市場價值以及公司總資產的波動率。
(2)估計違約距離。在KMV模型中,違約距離(DD)被定義為公司總資產未來市場價值的期望值與違約實施點(DP)的差,違約距離(DD)等于為到達違約實施點(DP)公司資產價值需下降的百分比對于標準差的倍數,違約距離(DD)實際上就是公司資產市值偏離違約實施點(DP)的標準差的個數。在KMV模型中,最普遍的違約距離(DD)計算公式為:

(3)估計違約概率。由于KMV模型認為,當公司資產市值低于違約實施點(DP)時,公司即會發生債務違約,那么違約概率就是指企業公司資產市值降低到違約實施點(DP)以下的概率,是與公司債務的絕對值(債務額)和相對值(債務人公司資產結構)有關的變量。通過建立公司總資產市場價值及波動率與公司股票價值及波動率之間的關系模型,可以有效地估計公司總資產市場價值的分布情況,從而可以計算公司資產市值低于違約觸發點的概率。若假定違約距離(DD)服從標準正態分布,那么它與違約概率(EDF)有如下關系成立:

(三)K M V 模型參數的確定 首先,對KMV模型中股權市場價值計算方法進行調整,根據確定的各項參數,通過聯立方程組求出未知的兩項VA和σA解。其次,計算在三種違約實施點(DP)值情況下,樣本上市公司的違約距離(DD),從而求出違約概率EDF。最后,要對對比公司樣本的違約距離(DD)做T檢驗,以判斷ST公司與非ST公司兩組樣本之間違約距離是否有統計上顯著的差異,從而通過KMV模型鑒別上市公司的整體信用風險的情況。
二、樣本進取與檢驗
(一)樣本選取 本文選取了2009年上海及深圳股票交易所被ST的10家上市公司以及與之配對的10家未被ST的公司數據作為研究樣本,取得共20家公司2007年12月31日至2009年12月31日期間的股票市場和財務數據。計算基準日為:2007年12月31日、2008年12月31日和2009年12月31日。為最大限度的避免非財務因素(如:樣本公司處于不同行業、公司間規模差異較大、不同股票市場的投資者存在整體差異等因素)的不利影響,選擇用以比對的ST上市公司與非ST上市公司時有以下三條原則:配對公司屬于同一行業且主營業務基本相同;配對公司資產總額接近;配對公司在同一個證券交易所上市。
(二)檢驗分析 首先根據上市公司的財務數據和市場數據確定出各上市公司的違約點、股權價值、股權價值波動率,然后使用Matlab軟件解非線性聯立方程組可求得公司資產的市值和資產價值波動性,再結合式(3)可以求出上市公司的違約距離。
(1)違約點的選取與股票市值計算。KMV模型認為,公司決定是否對其債務違約,與公司總資產的市場價值有很強的關系,當公司總資產的市場價值過低時,公司就會決定對其債務進行違約。KMV模型假設存在一個公司資產價值的水平,當公司總資產的市值低于該水平時,債務違約就會發生。那么,該水平就是公司的違約實施點(DP),可以看出,公司的違約實施點(DP)也就是這一水平上的公司總資產的市場價值。本文采用KMV模型中違約實施點的普遍計算方法:DP=流動負債+50%長期負債(如表1所示)。計算資產價值及其波動性首先需計算公司的股票市值。由于我國的上市公司存在流通股和非流通股之分,非流通股沒有市場價格,無法精確估計其股權的真實價值,因此本文采用了每股凈資產來代替股票的交易價格。所得結果如表1所示:
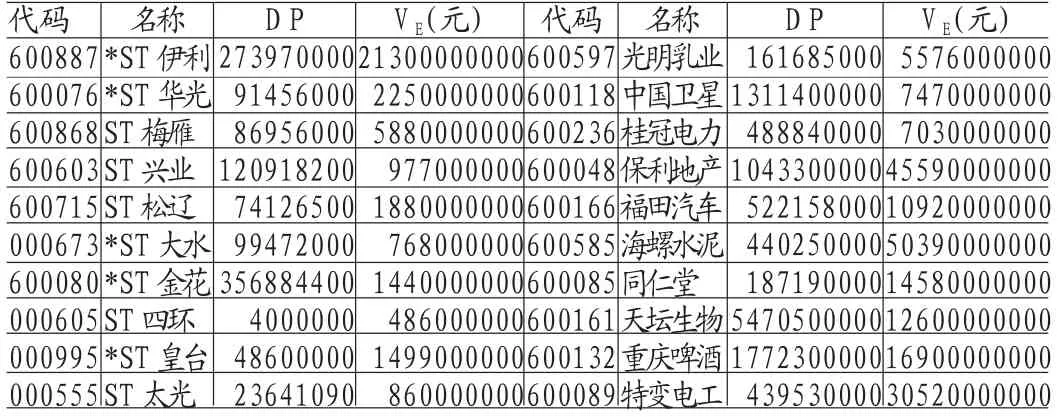
表1 ST 公司與非ST 公司2009年違約點、股票市值
(2)資產市場價值及波動率的計算。首先,本文采用歷史波動率法,分別選取每年同三個月份中(本文選為每年6-8月)每個交易日股票的收盤價來計算波動率,進而可以得出年收益波動率。其次,根據式(1)與(2)聯立方程組,運用Matlab軟件,代入已知變量和求出的相關變量即可結算出結果。樣本公司2007與2009年資產市場價值與波動率計算結果如表2所示。再次,公司總資產未來市場價值的期望均值與違約實施點的差在KMV模型中即為為公司的違約距離。可以根據計算樣本公司的違約距離,計算結果如表2所示。

表2 ST 公司與非ST 公司2009年資產市場價值與波動率、違約距離的計算
(3)違約概率的計算。如果已知企業資產的概率分布,就能由違約距離來求出違約概率。一般情況下,假設企業的資產價值是服從正態分布或者對數正態分布,根據公式EDF=(1-N(DD))*100%從而計算出理論上的違約概率。如表3所示:
(4)對違約距離做T檢驗。為了比較ST上市公司與非ST上市公司這兩組數據之間,違約距離(DD)是否有統計上的顯著性差異,本文對兩個對比公司的樣本數據進行了T檢驗。兩對比公司樣本之間的T檢驗是根據樣本公司的數據對樣本來自的兩對比公司樣本的期望值是否具有差異的顯著性得出結論和推斷,用來檢驗兩對比公司樣本是否具有顯著性差異。本文運用Eviews軟件對2009年所選對比樣本ST與非ST公司的資產不良率即資產價值年增長率(自變量:Y)和違約距離(因變量:X)進行回歸分析,所得結果如表4所示:
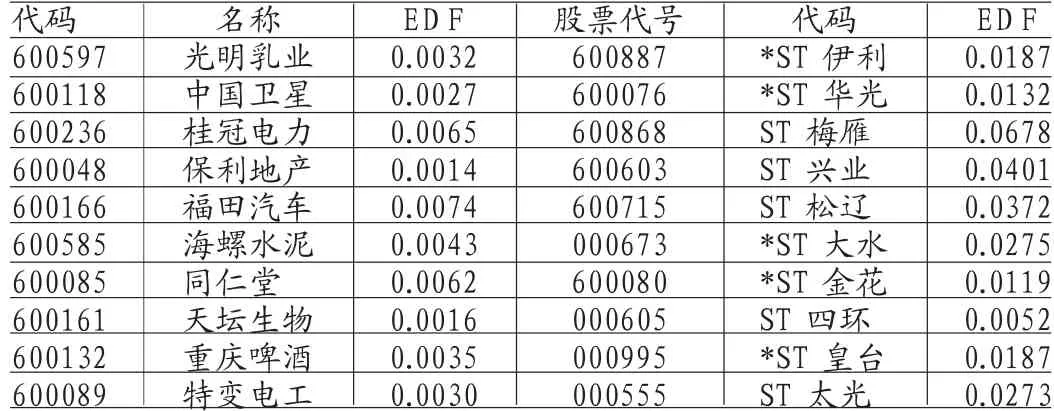
表3 ST 與非ST 公司2009年的違約概率

表4 違約距離檢驗
通過回歸分析可以發現結果十分顯著性,因此可以據此對違約距離(DD)的T檢驗結果進行總結性分析。違約距離(DD)是指公司總資產市場價值的期望均值相對于公司違約實施點(DP)的偏離程度,該偏離程度的大小用以衡量公司距離發生債務違約的距離大小,偏離程度越大,公司就越不可能發生債務違約事件,偏離程度越小,則表示公司離還款違約已經不遠了。如表4所示,兩組對比公司之間樣本數據計算得到的違約距離(DD)平均值之間的差為1.0041,以上數據證明,從統計上看,非ST公司總資產的市值期望值遠遠高于其違約實施點(DP)上資產市值的水平,而ST公司總資產的市值期望值則離違約實施點(DP)上資產市值的水平較近,即表明與ST公司相比,非ST公司發生債務違約的可能性要低很多。在T檢驗這一端,當取95%的顯著性水平取時,不論是ST公司還是非ST公司,其違約距離(DD)的檢驗結論均滿足T檢驗的顯著性要求,這表明從統計上看,在ST公司和非ST公司之間,違約距離(DD)之間具有顯著的差別。實證分析表明,ST公司與非ST公司兩組樣本之間違約距離有著顯著的差異。因此,在統計上證明了KMV模型的實用性:在能提供充足歷史數據的情況下,KMV模型確實能夠較好的分辨經營較好的公司與經營較差的公司在違約可能性上的差別。
三、結論
本文在全面剖析KMV模型的基礎上,并用其作為工具對我國上市公司信用風險變動做了檢驗分析,檢驗結果表明,ST公司與非ST公司兩組樣本之間違約距離差異非常顯著,因此可以看出,利用KMV模型能夠較好地識別出非ST公司和ST公司之間信用風險的差別,具有很強的風險預警能力。盡管KMV模型本身存在一些缺陷,我國證劵市場信息披露以及數據庫的建設滯后等均影響到模型有效的發揮,但由于KMV模型較強的理論基礎以及計算操作的模塊化,可以相信,隨著資本市場信息披露的不斷完善以及模型的進一步完善,KMV模型用于識別與評價公司信用風險的優點會越來越明顯。
[1]閆麗瑞:《基于K M V 模型的信用風險度量研究》,《山西財經大學學報》2009年第5期。

