高考題中平拋運動最值問題的探秘與賞析

陳曉東

(江蘇省石莊高級中學 江蘇 南通 226531)

筆者仔細分析了2010各地高考題，發覺江蘇、重慶、浙江三地都在計算題中以平拋運動為載體，考查了求最值的問題，應該說試題的綜合性較強、靈活性較大，凸顯了中學物理教學大綱所提出的“運用數學解決物理問題的能力”．乍一看，給人耳目一新的感覺，但細細回味，不難發現這些題的“原型”其實都很熟悉，而且這一“源”題都做過、考過．無非是用新瓶包裝了一下，里面裝的還是陳酒．本文對此進行了歸納整理，與大家探討．

【例1】(2010年高考江蘇物理卷第14題)在娛樂節目中，選手需要借助懸掛在高處的繩飛越到水面的浮臺上，小明和小陽觀看后對此進行了討論．如圖1所示，他們將選手簡化為質量m=60 kg的質點， 選手抓住繩由靜止開始擺動，此時繩與豎直方向夾角α=30°，繩的懸掛點O距水面的高度為H=3 m.不考慮空氣阻力和繩的質量，浮臺露出水面的高度不計，水足夠深．取重力加速度g=10 m/s2，sin53°=0.8，cos53°=0.6.

圖1

(1)求選手擺到最低點時對繩拉力的大小F；

(2)若繩長l=2 m,選手擺到最高點時松手落入水中．設水對選手的平均浮力f1=800 N，平均阻力f2=700 N，求選手落入水中的深度d；

(3)若選手擺到最低點時松手， 小明認為繩越長，在浮臺上的落點距岸邊越遠；小陽認為繩越短，落點距岸邊越遠，請通過推算說明你的觀點．

解析：(1)由機械能守恒

(1)

質點作圓周運動，由向心力公式，有

解得

F′=(3-2cosα)mg

人對繩的拉力

F=F′

則

F=1 080 N

(2)由動能定理

mg(H-lcosα+d)-(f1+f2)d=0

解得d=1.2 m.

(3)選手從最低點開始做平拋運動x=vt

且由式(1)，解得

因此，兩人的看法均不正確.當繩長越接近1.5 m時，落點距岸邊越遠.

圖2

(1)求繩斷時球的速度大小v1和球落地時的速度大小v2．

(2)輕繩能承受的最大拉力多大？

(3)改變繩長，使球重復上述運動，若繩仍在球運動到最低點時斷掉，要使球拋出的水平距離最大，繩長應是多少？最大水平距離為多少？

由機械能守恒定律，有

得

(2)設繩能承受的最大拉力大小為T，這也是球受到繩的最大拉力大小．

得

(3)設繩長為l，繩斷時球的速度大小為v3，繩承受的最大拉力不變，有

得

繩斷后球做平拋運動，豎直位移為d-l，水平位移為x，時間為t1,有

得

【例3】(2010年高考浙江物理卷第22題)在一次國際城市運動會中，要求運動員從高為H的平臺上A點由靜止出發，沿著動摩擦因數為μ的滑道向下運動到B點后水平滑出，最后落在水池中．設滑道的水平距離為L，B點的高度h可由運動員自由調節(取g=10 m/s2)．求：

(1)運動員到達B點的速度與高度h的關系；

(2)運動員要達到最大水平運動距離，B點的高度h應調為多大？對應的最大水平距離smax為多少？

(3)若圖3中H=4 m，L=5 m，動摩擦因數μ=0.2，問水平運動距離要達到7 m，h值應為多少？

圖3

解析：(1)由A運動到B過程，有

(2)平拋運動過程中

解得

smax=L+H-μL

h2-3h+1=0

解得

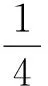
圖4

(1)小球剛運動到B點時，對軌道的壓力多大?

(2)小球落地點C與B的水平距離s為多少?

解析:(1) 小球沿圓弧做圓周運動,在B點由牛頓第二定律，有

從A到B，以B點為零勢能點，由機械能守恒定律,有

由以上兩式得NB=3mg，由牛頓第三定律，得小球對軌道的壓力為3mg.

(2)小球離開B點后做平拋運動,拋出點高為H-R，有

s=vBt

解得

smax=H

評析：以上列舉的3道高考題都很新穎，其中在知識方面綜合考查了牛頓運動定律、平拋運動、圓周運動、勻變速直線運動、機械能守恒定律、動能定理等大綱中明確要求學生理解并掌握的知識點；能力方面考查了求解平拋運動中最大水平分位移的問題；在具體求解時，源題與3道高考題都用到了高中數學中所學的極值定理．比較起來，無論是知識上還是能力上，幾道高考題與源題都有驚人的相似之處，都是在源題的基礎上換了一下情境，其實大多數題追根溯源，都能找到它的“活水源頭”.作為一線教師，在平時除了要把題目講精、講透外，還得注重適當的拓展延伸，有效進行知識的遷移和應用，著力培養學生的發散性思維能力，以不變應萬變，在知識、方法和能力等方面全面貫徹新課程理念．