金屬內襯復合結構的固化模擬研究

馬 李，趙先銳

（臺州學院 物理與電子工程學院，浙江 臺州 318000）

金屬內襯復合結構的固化模擬研究

馬 李，趙先銳

（臺州學院 物理與電子工程學院，浙江 臺州 318000）

為評價帶有金屬內襯的復合材料構件固化工藝制度，采用有限元方法對其進行二維溫度場和固化度場的分布模擬。在模型中通過有限差分法考慮了溫度與固化度的耦合作用，建立了帶有金屬內襯的復合材料構件固化工藝數學模型。數值計算結果表明：復合材料的厚度可以加劇構件的固化速率及溫度梯度；金屬內襯在固化過程中更像一個吸熱器，起到減緩溫度梯度和固化速率的作用。計算結果與實驗數據符合較好，驗證了模型數值結果的可靠性。

有限元方法；溫度；固化度；耦合

1 引言

復合材料經常與金屬材料作為結構一同使用，例如復合材料導彈彈翼中需要加入鈦合金骨架，蜂窩夾層結構中的復合材料蒙皮和鋁蜂窩，金屬內襯纖維纏繞復合材料壓力容器。決定復合材料構件的質量關鍵是合適固化工藝，不適合的固化工藝產生的殘余應力可能使結構在未施加機械負荷之前產生裂紋、脫層和局部屈曲，這種“前負載”的影響使強度降低。

確定合適的固化工藝是一個復雜的問題，其工藝參數是通過大量的試驗來確定的，實驗方法的局限性在于：難于全面、準確了解固化過程中各種參數的變化和空間分布以及對最終固化效果的影響。在實際過程中，較厚的復合材料構件只能不惜延長固化時間，盡量降低升溫速率或者增加中途恒溫次數來維持材料溫度均勻，這必然導致生產成本的增加［1］；對于大型、幾何形狀復雜的實際結構，試驗方法的局限性顯得更為突出。因此，采用數值模擬方法研究固化過程中各種重要的參數如固化度，溫度場，黏度，氣泡的尺寸，殘余應力等［2，3］的變化規律，以期獲得合理、經濟的固化工藝，是一項重要的研究工作，吸引了越來越多的工作者的關注［4-7］。

本文采用有限元法，針對帶有金屬內襯的纖維纏繞復合材料構件這一類結構的成型固化過程進行分析和研究，探討了固化構件中復合材料的厚度和金屬內襯對固化結果的影響。本文模型的數值計算結果與試驗的數據進行了比較，驗證了模型可靠性。

2 基本原理

2.1 熱傳導方程和固化動力學方程

復合材料固化過程是一個傳熱和化學反應相耦合的非線性內熱源問題，其中內熱源來自樹脂基體內部的聚合交聯放熱反應。Fourier熱傳導方程為

式中：ρ為密度；cp為比熱；T為溫度；λ為熱導率；q單位時間內由于固化反應所產生的熱量；下標表明方向。其中垂直纖維方向的熱導率為［8］：

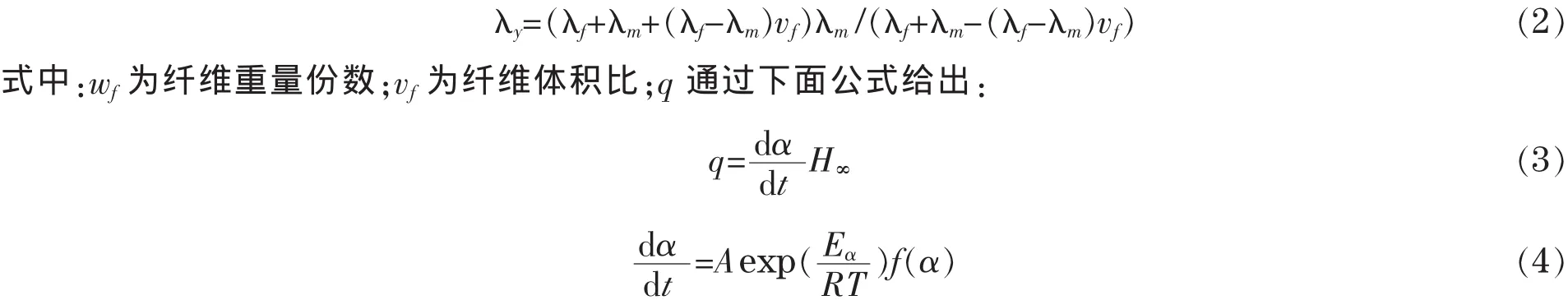
式中H∞為單位質量固化反應放熱量；Eα為激活能；A為指前因子；R為氣體常數；f（α）為機理函數，本文機理函數為（1-α）n，可通過DSC技術獲得。

2.2 離散方程和求解過程將方程

由于αt為上一步計算值已知，（）t+△t△t也事先由固化動力學模型確定，很容易得到αt+△t。熱源項與固化度相耦合，二者本質上是時變的。當時間增量取得足夠小時，在該時間增量內可以將熱源項近似為常量，利用方程（5）求解溫度場。然后，用方程（6）計算固化度。并修正下一步的熱源荷載，重復上述過程直至固化結束。

3 有限元方法

計算模型為帶有金屬內襯的復合材料構件一部分，結構半徑為100cm，角度為5°。將問題設定為二維平面問題，從外到內分別為復合材料層、膠層、金屬層。建模過程中的三層材料為三個面，并且通過ANSYS的粘結技術（glue）成為一個整體，不會發生分開。劃分網格后，選擇的分析單元為plane55，單元數目為400，自由度為溫度，固化度通過差分法與溫度進行耦合。外層（復合材料層）圓弧邊施加邊界條件，固化構件在烘箱中固化成型，熱交換認為是第二類邊界條件，有效熱交換系數為25，其他三條邊線為絕熱條件文中采用。材料物理參數和樹脂體系熱動力學參數見表1。

表1 材料的物理和熱力學參數Table 1 physical and thermal property for the used material

4 結果討論與分析

4.1 厚度的影響

復合材料厚度選擇0.5cm，1.5cm，3.0cm，樹脂含量為30%進行計算，固化周期選用生產商推薦的工藝（MRC）。構件底處溫度歷程在圖1中給出，橫坐標每一個間隔代表2秒時間。縱坐標代表溫度T/℃。可以看出，在橫坐標為4000左右，1.5cm和3.0cm構件溫度分別超過0.5cm構件。在橫坐標達到8000右，0.5cm構件溫度反超1.5cm和3.0cm構件。圖2給出了構件底部的固化歷程，在橫坐標4000左右，厚的復合材料構件底部固化速率加快，固化程度G相應的超過了厚度為1.5cm和0.5cm的，這與溫度歷程中3種厚度構件第一次溫度變化相對應，第一次溫度變化主要是由于樹脂固化相關。可以解釋為復合材料熱傳導率低，厚的復合材料層的固化放熱無法很快傳出，使其底部溫度升高，固化速率加快。隨著厚度的增加，固化放熱對溫度貢獻的效應愈加明顯。而對于第二次溫度變化，三種厚度的復合材料固化都已接近完全，所以固化放熱的影響并不起主要的作用，該溫度變化應該歸結為復合材料導熱率低，復合材料構件厚薄造成的。

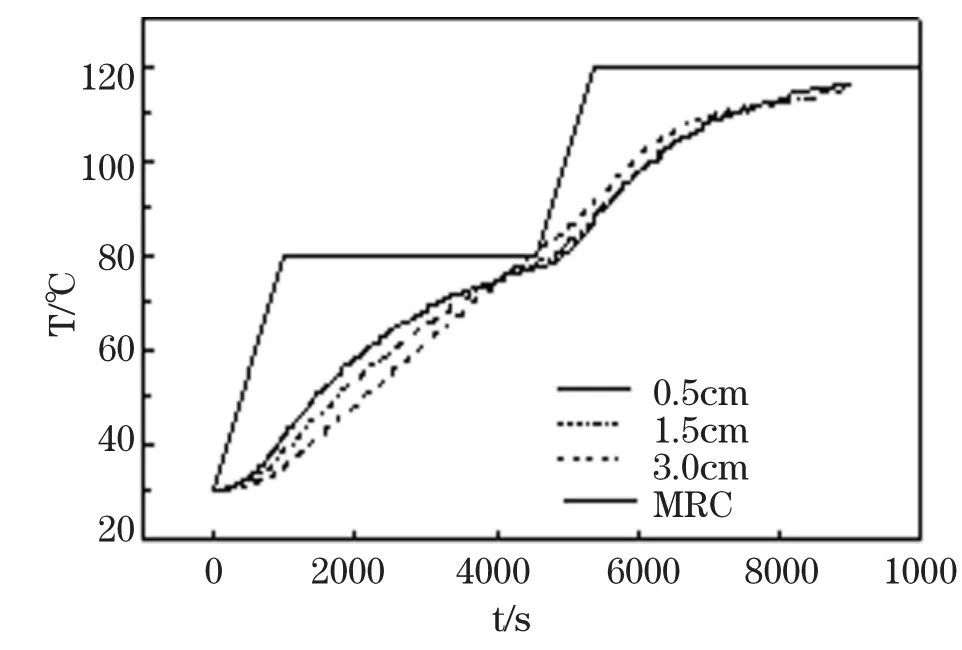
圖1 不同厚度復合材料中心處溫度對比Fig.1 Comparison of the history of temperature at center of composites with various thicknesses

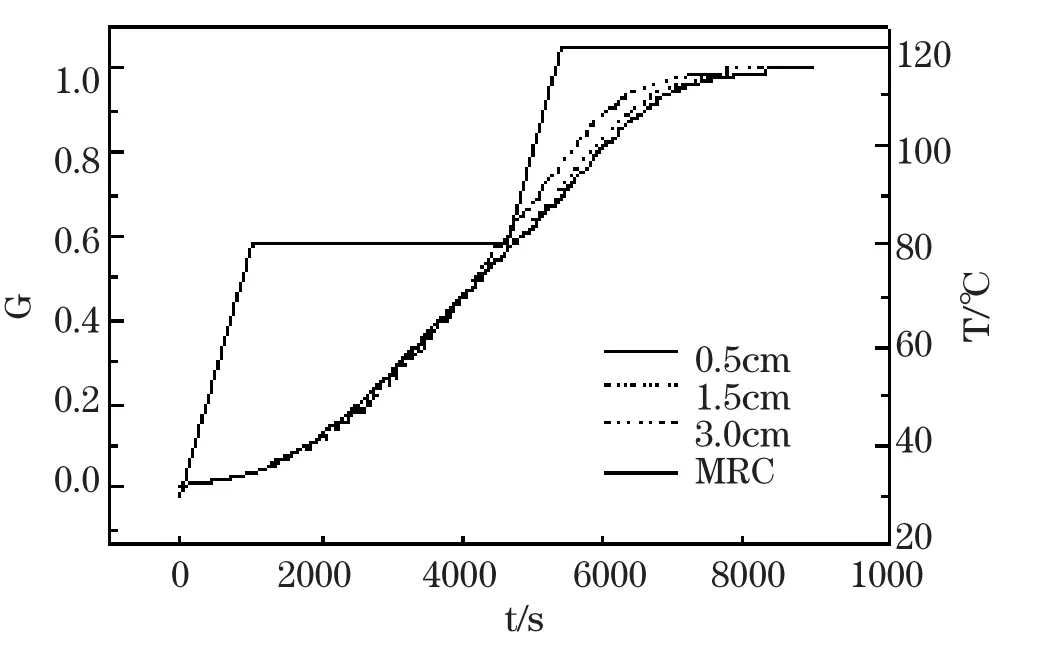
圖2 不同厚度復合材料固化對比Fig.2 Comparison of the history of cure at center of composites with various thicknesses

4.2 金屬內襯的影響

對于金屬內襯對固化構件的影響，本文選擇了復合材料層厚為1.5cm，樹脂含量為30%，金屬內襯厚度分別為2.0cm，1.0cm，0.1cm進行分析。圖3給出了三種金屬內襯厚度復合材料溫度歷程的對比曲線。可以看到，隨著金屬內襯厚度的減少，溫度突變越加明顯，正如金屬內襯為0.1cm所示，在橫坐標達到2000左右，溫度已經接近120℃。分析可知，溫度突變主要貢獻者應該是樹脂固化放熱，圖5給出了不同金屬內襯厚度的復合材料底部的固化歷程。可以看到，在相同的邊界條件下，相比與金屬內襯厚度2.0cm，1.0cm固化歷程，具有厚度為0.1cm金屬內襯的復合材料固化速率非常快，在第一個平臺溫度時接近完全。對比復合材料內外固化速度，具有0.1cm金屬內襯的復合材料構件開始階段固化是從外部到內部。由于固化放熱影響，復合材料構件的固化順序發生變化，內部的固化超過了外部的固化速度。而對于金屬內襯厚度為1.0cm，2.0cm，固化都是從外部到內部。以上的計算分析可知，金屬內襯的厚度不僅影響了構件的固化速度，也可以改變了構件內外的固化順序。而這些是因為金屬內襯在構件的固化過程中，不僅不放出熱量，還通過吸收固化放熱改變自身的溫度，即發揮著吸熱器的作用。同時，溫度與固化度之間的強耦合作用，使金屬內襯的厚度改變了構件的內外的固化順序。金屬內襯的以上調節作用，使其在固化構件中，不僅要考慮其結構中的作用，而且在固化過程中起的作用也應考慮。這樣可以避免在給定的固化制度下，過快固化速度導致固化不均勻及外層先固化均可能導致空氣無法排除而使孔洞的產生。

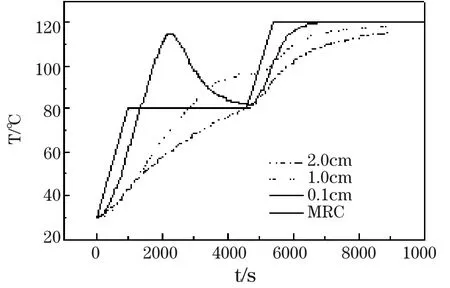
圖3 不同厚度金屬內模的復合材料溫度歷程Fig.3 Comparison of the temperature history of composites with different thickness metal mold

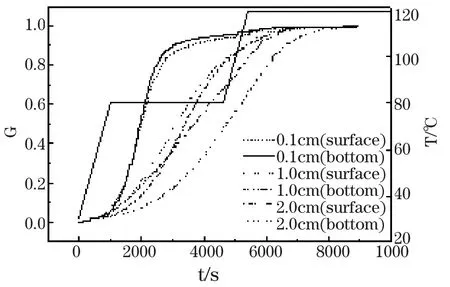
圖4 不同厚度金屬內模復合材料固化歷程對比Fig.4 Comparison of the cure history for composite with different thickness of metal mold

4.3 試驗驗證

為驗證分析模型的準確性，本文進行了驗證性試驗。復合材料固化測試的數據一般應包括溫度，固化度，黏度等。因溫度測量快速方便，所以通常采用溫度測量。試件采用碳纖維T700/epoxy，濕法手鋪層合板，復合材料中心處放二個熱點偶，測量固化構件的溫度。在烘箱中固化成型，烘箱中放入一個熱電偶測量烘箱環境溫度。圖5給出計算數據與實驗數據對比結果，吻合的較好，說明了計算模型的可靠性。

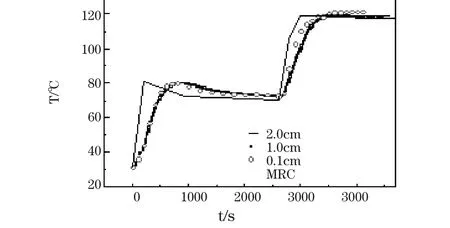
圖5 實驗測試溫度與模擬數據對比Fig.5 Comparison of temperature measured with data calculated by simulation

5 結論

建立了帶有金屬內襯纖維纏繞復合材料構件固化分析的數學模型，結合有限差分法考慮溫度及固化度的強耦合關系。并通過試驗驗證了分析模型的準確性，為帶有金屬內襯的復合材料構件固化過程中的分析計算提供保證。構件的復合材料厚度可以影響溫度梯度及固化速率；因金屬內襯在固化過程中起到吸熱器作用，使其不僅可以改變固化構件的固化速率，同時可以改變內外的固化順序。

［1］李辰砂，張博明，王殿富，杜善義．用數值模型研究復合材料固化過程規律［J］．復合材料學報，2000，17（4）：92-99.

［2］P R.Ciriscioli et.al..Autoclave curing-comparisons of model and test results ［J］.Journal of Composite Materials.1992，26（1）：90-102.

［3］Madhu S，Madhukar，M S Genidy. A new method to reduce cure-induced stresses in thermoset polymer composites，Part I： test method ［J］.Journal of Composite Materials.2000，34（22）：1882-1903.

［4］Park H C，Lee S W.Curing simulation of thick composite using the finite element method ［J］. Journal of Composite Materials.2001，35（3）：188-201.

［5］Neeraj Rai，Ranga Pitchumani.Optimal cure cycles for the fabrication of thermosetting-matrix composites［J］.Polymer Composites.1997，8（4）：566-581.

［6］Loos A C，Springer G S.Curing of epoxy matrix composites ［J］.Journal of Composite Material.1983，17（2）：135-169.

［7］Jianhua Li， Sunil C.Joshi，Y.C.Lam.Curing optimization for pultruded composite sections［J］.Composites Science and Technology.2002，62（3）：457-467.

［8］戴福洪，吳湛君，張博明，杜善義.復合材料RTM成型工藝固化過程的三維數值模擬［J］.復合材料學報.2004，21（5）：134-139.

［9］R C Wetherhold. Difficult in the theories for predicting transverse thermal conductivity of continuous fiber composite ［J］.Journal of Composite Materials.1994，28（15）：1419-1498.

A Study of Simulation of Curing Process of Composite Component with Internal Metallic Mold

MA Li，ZHAO Xian-rui
（School of Physics and Electronics Engineering,Taizhou University,Taizhou 318000,China）

To evaluate cure cycle of composite component with internal metallic mold,finite element method was employed in numerical simulation of its two-dimension temperature and cure degree field distribution in this paper. Mathematical model was established to describe cure process of composite component with internal metallic mold during filament winding process, and the coupling between temperature and cure degree was considered using finite difference method in the model.Numerical results show that the thickness of composite component affects the rate of cure and temperature gradient.Internal metallic mold plays a role in a heat-sink,which slows up the gradient of temperature and the rate of cure.Compared with experimental data,the relia

bility of the model established in this paper was proved.

finite element method;temperature;cure degree;coupling

周小莉）

TG156.8

A

1672-3708（2012）03-0035-05

2011-10-08

臺州市科技計劃項目（100KY64）

馬 李（1974- ），男，黑龍江哈爾濱人，博士，副教授，主要從事復合材料結構方面的研究。