邊坡模糊隨機可靠性分析的模糊點估計法

王 宇 ，賈志剛李 曉汪 燦余宏明

（1. 中國地質大學（武漢）工程學院，武漢 430074；2. 中國科學院地質與地球物理研究所，北京 100029；3. 中國科學院研究生院，北京 100049）

1 引 言

邊坡工程中不可避免地涉及到大量的不確定性因素，這些不確定性因素當中，既有隨機不確定性因素，也有模糊不確定性因素。隨機不確定性因素主要有荷載條件、地質環境、不同的施工環境與條件等；模糊不確定性因素主要體現在巖土體分類具有模糊性、邊坡的變形破壞特征具有模糊性、巖土體的物理力學參數具有模糊性等。因此，對于邊坡這樣一個復雜的地質系統，單純用可靠性理論來評價是不夠的，它要求既要考慮到因素的隨機性，同時更要考慮到因素的模糊性。

將模糊理論應用于邊坡工程，國內外學者已經作了一些相關性的研究工作，并取得了一定成就[1－7]，但其中存在著許多問題亟需解決。如文獻[1]用“梯形模糊數”計算穩定系數區間，僅考慮了隨機變量的兩種簡單組合情況，然后進行加權平均來計算可靠指標，準確性差；文獻[3]只是將隨機可靠性指標與模糊可靠性指標相加，從而得出模糊隨機可靠性指標，這種方法存在較大的片面性；文獻[4]將模糊測度理論應用于巖土邊坡穩定問題，對分析模型進行模糊化，但沒有考慮各個巖土力學參數的模糊性等。邊坡穩定模糊隨機可靠度的研究已有了一定的發展，但模糊理論與可靠度結合在邊坡工程中的應用仍然存在許多問題，主要體現在邊坡模糊評價標準的建立、隨機過程隸屬函數的確定等，其中比較突出的問題就是極限狀態變量模糊隨機可靠度的求解問題，因為它直接影響著邊坡穩定可靠性評價尺度的正確與否，決定工程決策的效益和損失。基于以上考慮，本文在前人的研究基礎之上，在統計矩點估計法（PEM）的基礎上，提出邊坡模糊隨機可靠性分析的模糊點估計法（Fuzzy-PEM），并考慮到巖土體物理力學參數的近似分布概型，采用區別于梯形模糊數的正態模糊數對巖土體力學參數進行模糊化處理，由PEM 求得可靠性指標。該方法不必知道狀態變量的概率分布，不需要求導，克服了傳統方法極限狀態方程概率密度函數構造困難、計算復雜、效率低的缺點。對復雜邊坡工程的可靠性分析具有很大的發展前景，為邊坡工程可靠性分析的理論與實踐提供了一條新的途徑。

2 PEM 基本原理

PEM 是由Rosenblueth 于1975 年提出的一種矩估計近似方法，于20 世紀80 年代初被引入結構工程的可靠性分析中。當各種狀態變量的概率分布未知時，只要它們的均值和方差，有目的的選擇或設計一些特殊組成的點（通常取2 個隨機變量均值對稱的2 個點），就可以求得狀態函數（穩定系數或安全儲備）的各階矩，且在狀態函數的假定概率分布條件下求得邊坡的可靠性指標[8]。

對一般的邊坡穩定性問題，取功能函數Z= g ( X ) = g ( x1， x2， … ， xn)，其 中 x1， x2， … ， xn為 重度、黏聚力、摩擦系數等影響邊坡穩定性的隨機變量。k 階原點矩用PEM 表示為[9－10]

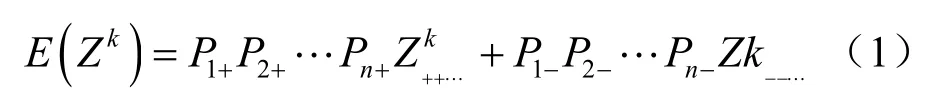
其中

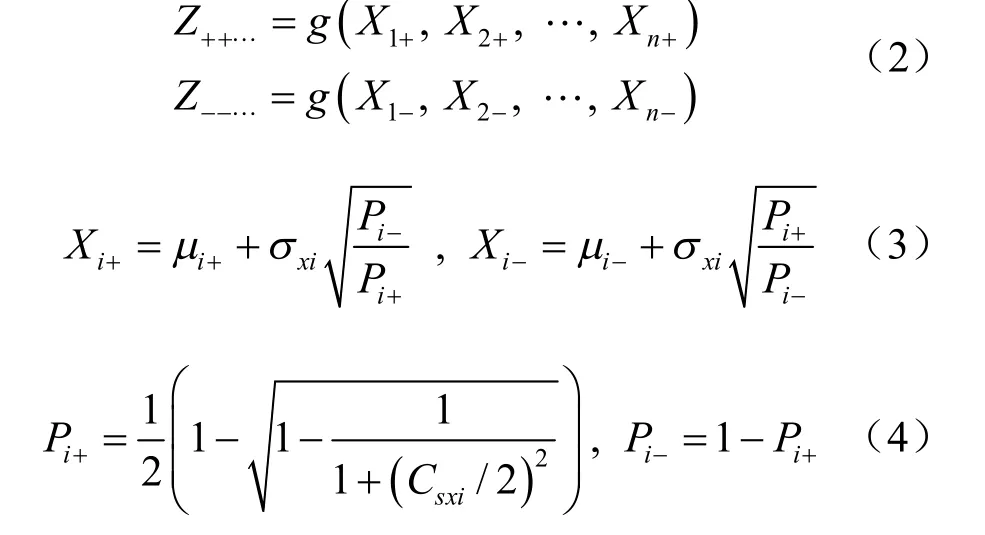
式中：sxiC 為隨機變量 iX 的偏度系數。當偏度系數未知時，可以假定sxiC =0，設n 個狀態變量互相關，則每一組合的概率jP 取決于變量間的相關系數ijρ ：

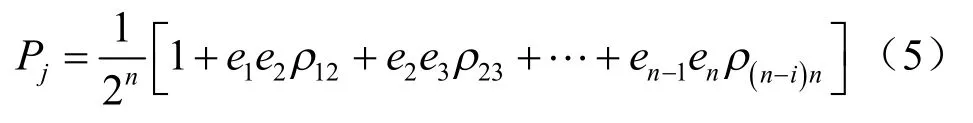
其中 ei（ i = 1， 2， … ， n）取值為：當 xi取 Xi+時，ei= 1；當 xi取 Xi-時， ei=-1 。

以功能函數 Z = g （ x ， y）為例，包含2 個隨機變量，每個隨機變量取2 個計算點，則有

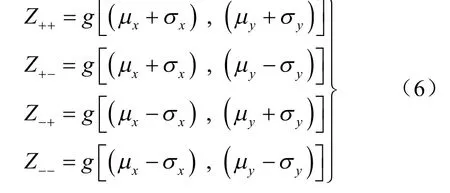
因此，功能函數Z 的期望和方差分別為

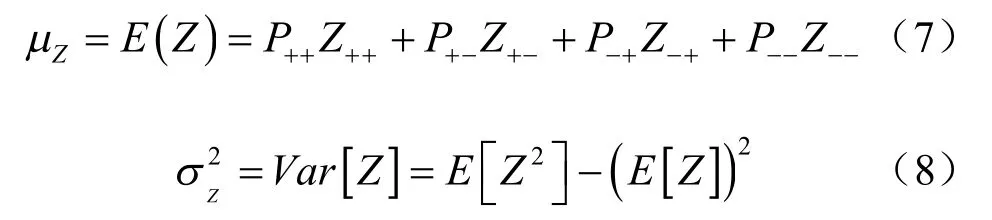
其中

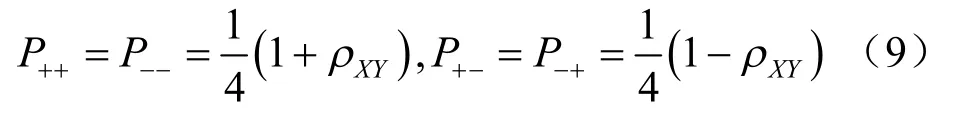
由此可求得邊坡的可靠性指標和破壞概率。

3 模糊隨機理論

3.1 模糊截集理論

傳統可靠性分析中計算量較大、方法單一、無法處理模糊變量等問題，應用模糊截集法可以實現模糊變量與隨機變量的相互等價轉換，使這一問題得以解決。對于普通集合來說，只有當隸屬度（ X0）=1時， X0才是屬于集合A 的。然而對于模糊集合，（ X0）=λ， λ ∈ ［ 0，1］，當且僅當（ X0）≥ λ時，才說 X0是中的元素。這樣，對 每個λ 都能從U 中確定一個普通子集，它是在λ這個信任程度上的反映，由此設∈F （ U），對?λ ∈ ［ 0，1］，稱

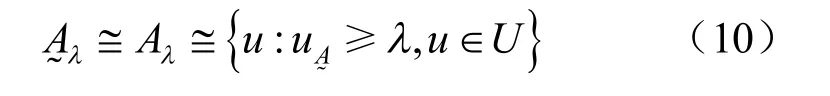
對于每個不確定變量，λ 截集能給出一個區間的2 個點，如對于每一λ 截集產生的上界值和下界值，這是進行模糊點估計的基礎。

3.2 隸屬函數的選取

巖土體物理力學參數既包含隨機特性，也包含模糊特性，應視為模糊隨機變量。為了研究物理力學參數的模糊性，可以通過模糊數來實現。模糊數大致可以分為線性和非線性2 種，由于當前的研究水平很難判斷哪種模糊類型更適合實際情況，因 此，現有的工程應用研究中大多采用線性模糊數形式，如梯形模糊數[1，12－13]。隸屬函數分布形式為

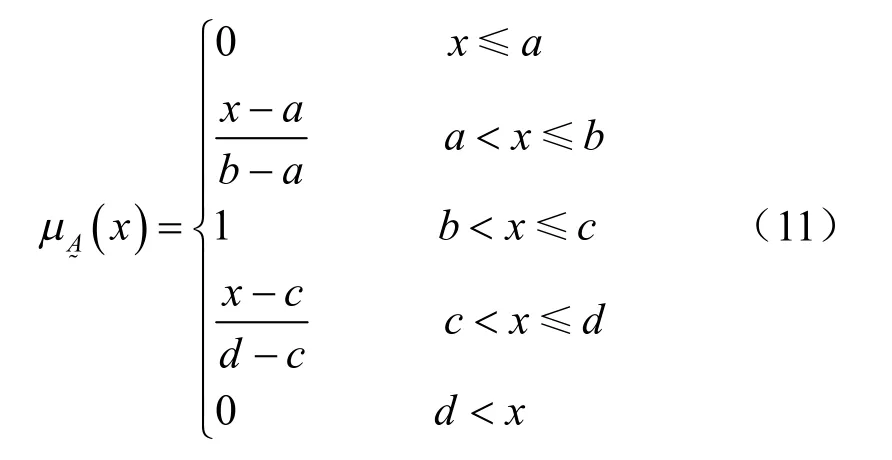
其曲線如圖1 所示。

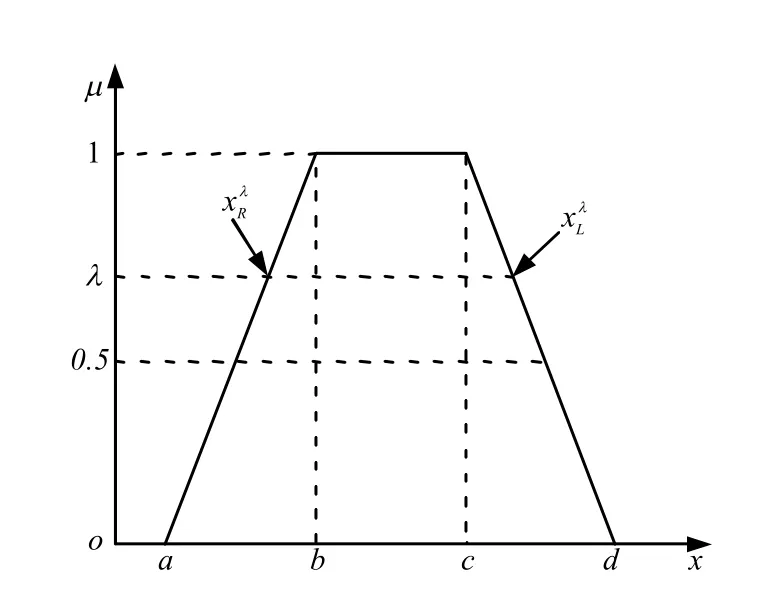
圖1 梯形隸屬函數 Fig.1 Trapezoidal membership function

然而，大量研究表明，巖土體物理力學參數如黏聚力、內摩擦角、土體重度等都近似符合正態或對數正態分布，采用線性模糊數來描述力學參數可能會導致一些重要隨機信息的丟失，因此，本文認為，采用正態模糊來描述物理力學參數應該更為合理。正態隸屬函數分布形式為

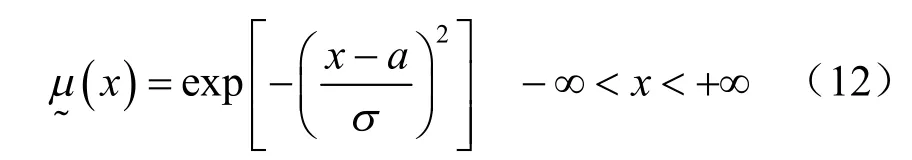
由于巖土體物理力學參數都是正數，因此，描述其模糊隨機性的正態模糊數應該都是有界正模糊數，可定義正態模糊數的隸屬函數為

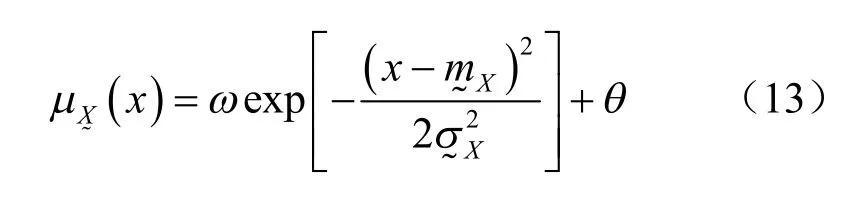
式中：Xm? 、Xσ? 分別為模糊數學期望值與方差。可用樣本的平均值和標準差估計；ω、θ 為2 個待定系數。

取向量映射的核ker，令 mX= ker

由性質有 ω + θ= 1；引入參數k，并使得

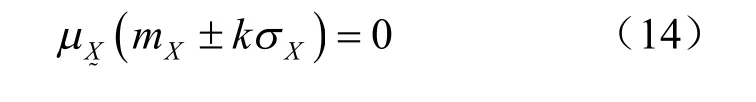
解式（14）得：

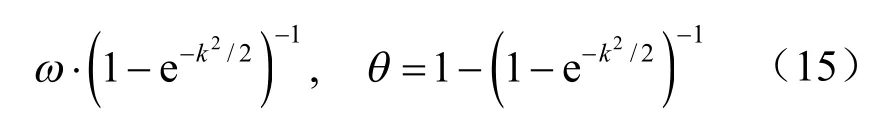
將式（15）代入式（13）得正態模糊數的隸屬函數表達式為

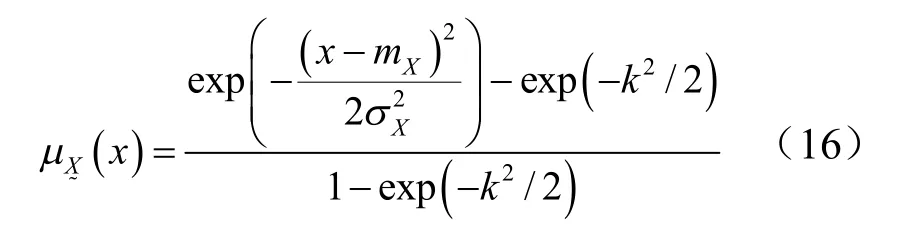
其函數圖形如圖2 所示。

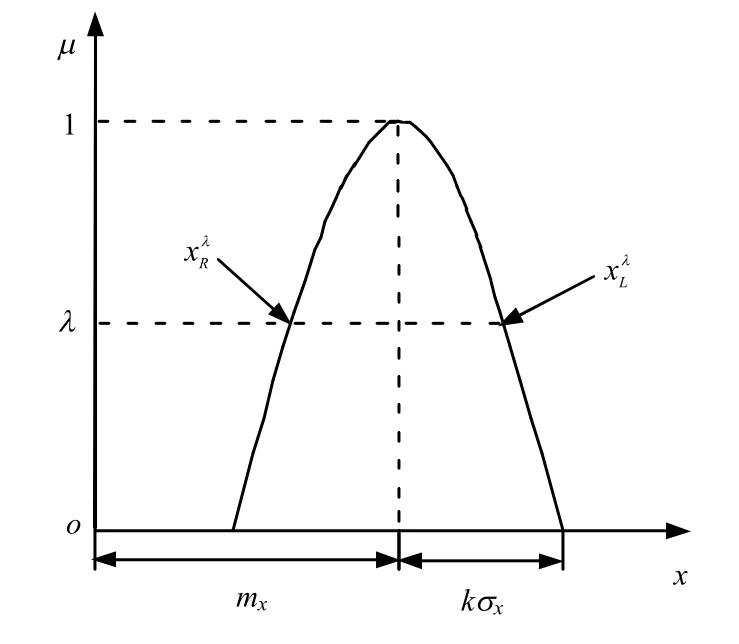
圖2 正態隸屬函數 Fig.2 Normal membership function

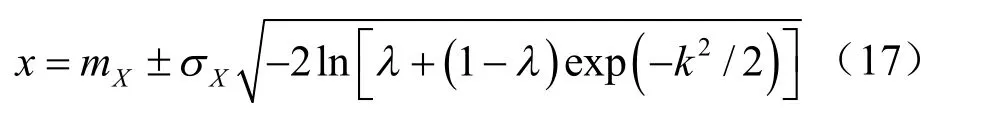
其中

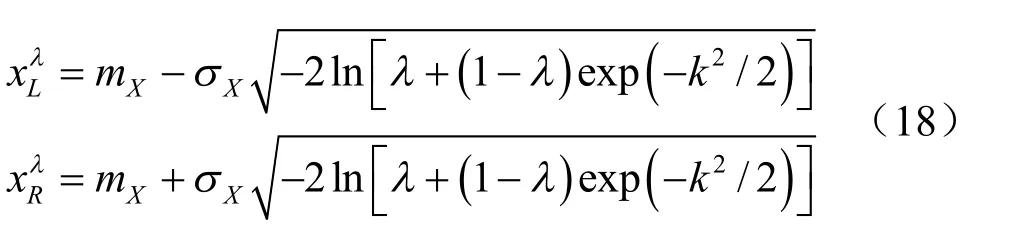
當x 近似服從對數分布時，由 lnY X= 服從正態分布，同樣可以推導出對數正態模糊數的隸屬函數表達式。

對應不同的隸屬度iλ ，可分別得到對應功能函數的點估計值，通過這樣的離散分析，可以更充分地考慮模糊變量的模糊性，從而得到更為合理的分析結果。

上式中參數k 控制著力學參數的最大取值空間，k 越大，則力學參數的區間越大，參數的置信度越低，選參越沒把握；反之亦然。一般認為，當參數為正態分布時，99.73%的數據落在( mX-3σX，mX+ 3σX)區間內，當邊坡巖土體的變異性較大，變異系數VX超過3 時，建議k 值取3。由力學參數非負性（即 mX- kσX≥ 0）可知， k ≤mX/σX= 1/ Vx。因此，k 的取值應根據邊坡工程的實際情況而定，在0.5～3.0 范圍內選取。

4 Fuzzy-PEM 原理

邊坡穩定性影響因素的隨機性和模糊性是客觀存在的，傳統的可靠性分析方法難以反映邊坡的真實工作狀態。本文提出的模糊點估計法則是一個更為合理的解決方法，它在處理過種中不需要知道模糊變量的具體特征，對影響邊坡穩定性的各個力學參數都進行模糊隨機處理，并在[0，1]區間上取有限個λ 約束水平，從而使得分析結果更加符合工程實際。

功能函數為 Z = g ( x1， x2， … ， xn)，考慮到隨機變量 xi的隨機性與模糊性，本文對每個變量 xi均采用正態模糊數處理。對應于不同的λ 水平，取不同的隸屬度，將分別得到對應的功能函數的點估計上限值和下限值（即上文中所指和），如圖2 所示。

當功能函數在[0，1]區間上取一個λ 約束水平時，得到λ 處r 階原點矩為

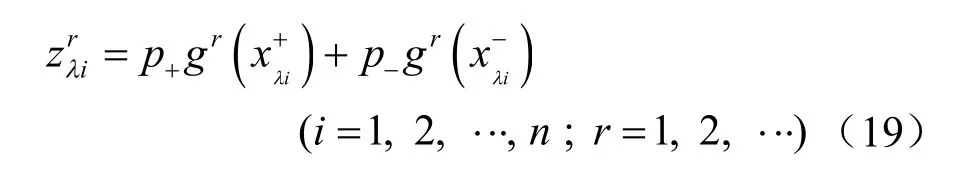
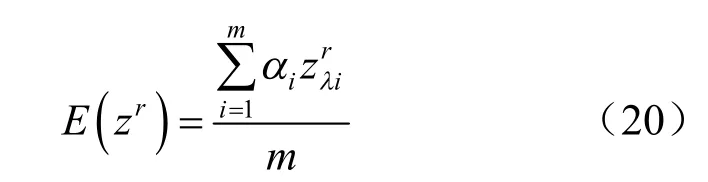
對比PEM 公式可以發現，式（20）中忽略了中間的(2n- 2)項，顯然是不準確的。因為PEM 公式中不僅有參數純上下界的組合，還有上下界混合在一起形成的組合。研究發現，當用正確的PEM 公式代入式（20）時，將得不出功能函數合理的k 階矩，因此，必須對式（20）進行修正。采用模糊理論中的加權平均思想，m 個λ 水平下考慮模糊隨機性的狀態函數的k 階原點矩為

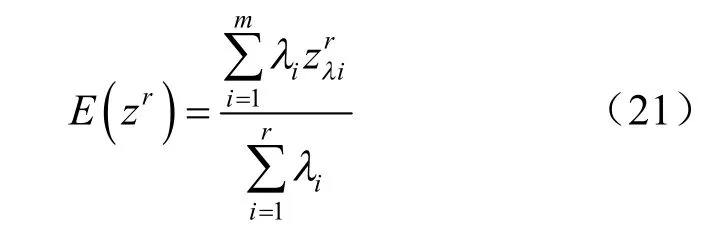
對邊坡工程來說，極限狀態函數 Fs的表達式為 Fs=g ( c， φ ， γ， H， …) ，當有n 個變量時，每個變量取2 個點，則有2n種組合，可由狀態方程求解2n個狀態函數值。因此，r 個λ 水平下考慮模糊隨機性的狀態函數的期望值和方差值分別為

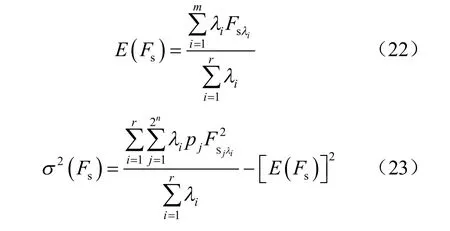
由此，可求得邊坡的模糊隨機可靠性指標為

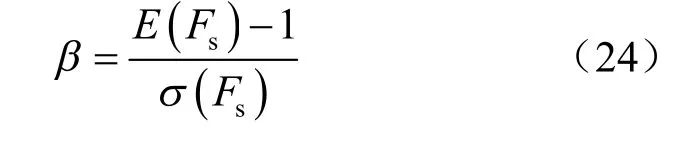
5 工程實例

5.1 研究區概況

岱家灣公路邊坡位于重慶市巫山縣兩坪鄉朝元村，順山坡展布。邊坡傾向南，邊坡高達112 m，長約200 m，上覆松散層厚一般10～20 m。坡體主要由碎石和充填其間的粉質黏土組成，碎石含量為50～60%，成分為泥灰巖，灰巖，粒徑為2～8 cm，個別達12 cm，棱角～次棱角狀；粉質黏土含量為40～50%，局部含量較高而成為含礫（碎石）粉質黏土透鏡體。鉆孔揭露無地下水。與其下伏基巖相比，松散的殘坡積碎石土抗剪強度較低，在一定的地形地質條件下可能成為潛在滑動面。在邊坡穩定性評價中，由于巖土體重度γ 的變異系數較小，將其視為定值不會帶來較大誤差，因而一般選取抗剪強度參數作為模糊隨機變量進行研究。邊坡巖土體物理力學參數服從正態分布，參數統計見表1。穩定性計算采用簡化的Bishop 法計算，借助于slide邊坡極限平衡分析軟件，視土條為剛體，用參數均值計算出的邊坡臨界滑動面見圖3。現擬對天然狀態下邊坡的穩定性進行可靠性評價。

本文對力學參數c 和φ 均采用正態模糊隸屬函數處理，考慮到實際邊坡力學參數的最大可能取值區間，取k = 1.5；為了盡可能地削除計算結果的離散性，取λ=0.1～0.9 9 個水平，按式（18）進行計算。各水平下的不確定性參數見表2。

表1 邊坡碎石土力學參數 Table 1 Gravel soil parameters of slope

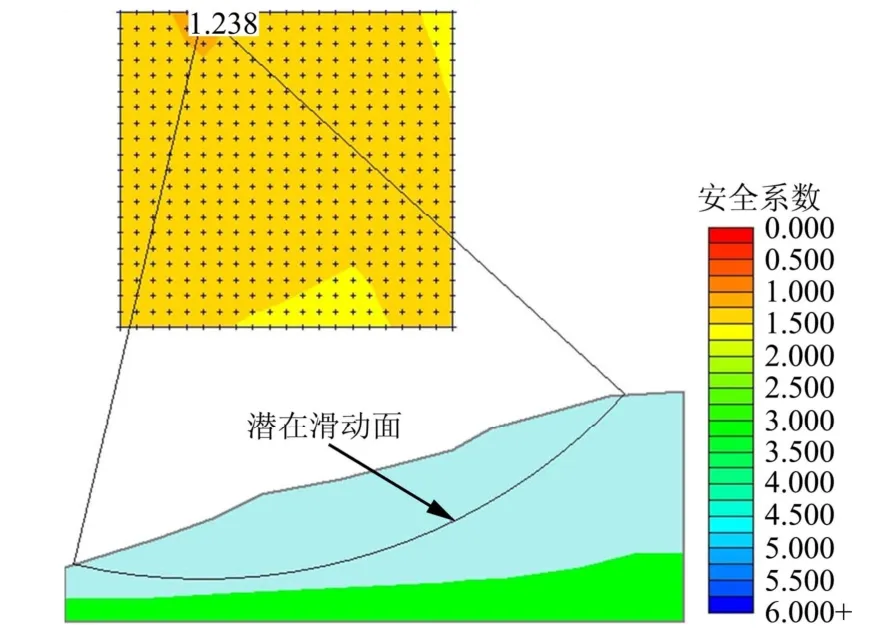
圖3 邊坡穩定性計算結果 Fig.3 Slope stability calculation result

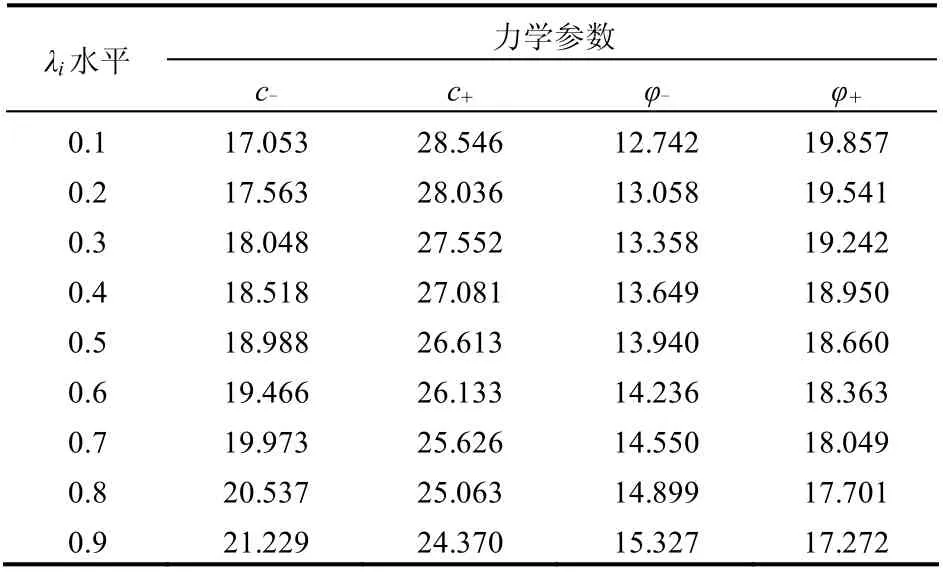
表2 λi水平下力學參數取值 Table 2 Mechanical parameters under different values of λi

5.2 結果計算與分析

本文不考慮參數間的相關性（ ρc，φ= 0），分別將不同水平的參數組合輸入到極限平衡法計算軟件中計算得出不同λ 水平下的點估計值，見表3。

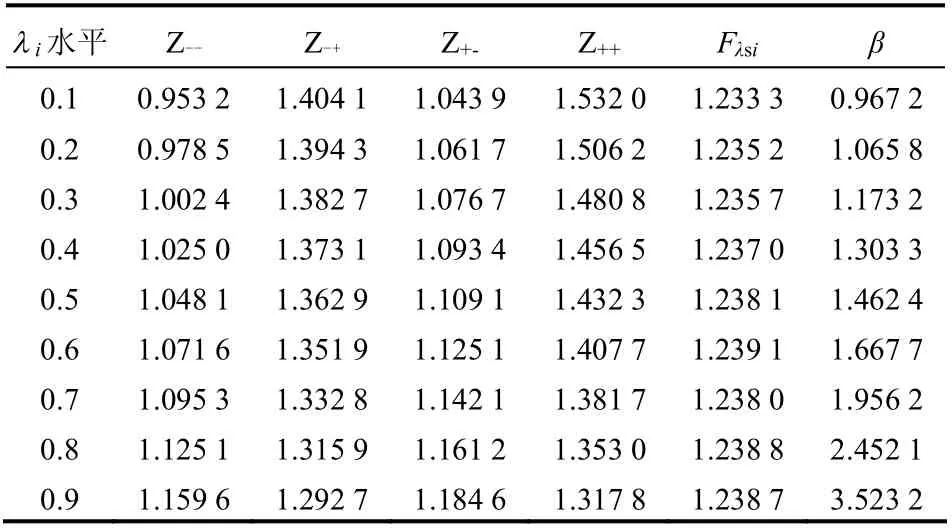
表3 iλ 水平各參數組合計算結果 Table 3 Results for different values of iλ

由表3 可知，模糊點估計法得出的不同λ 水平下的邊坡穩定系數在[1.233 3，1.239 1]間波動；隨著λ 水平的增大，可靠性指標增大，不同λ 水平下邊坡可靠性指標的波動區間為[0.967 2，3.523 2]。穩定系數、可靠性指標與λ 水平（隸屬度）的關系見圖4。由式（22）、（23）可以計算出穩定系數均值為1.238 0，標準差為0.140 3，因此，邊坡的模 糊隨機可靠性指標β = 1.696 6，破壞概率為Pf= 0.044 9。

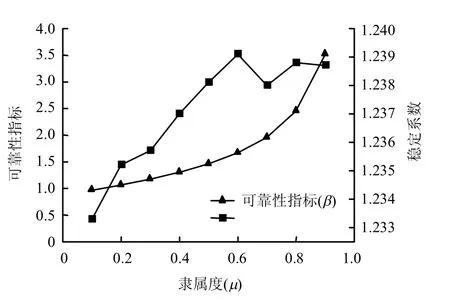
圖4 穩定系數、可靠性指標與隸屬度的關系 Fig.4 Relationships between FS and β vs. μ

為了便于說明計算結果的可靠性，同時用不考慮力學參數的統計矩點估計法、通過構造概率密度函數的模糊概率方法對該邊坡進行了可靠性分析，見表4。

表4 不同計算方法結果對比 Table 4 Comparison of reliability results obtained by different methods

由表4 可以看出，模糊點估計法計算結果和模糊概率法所得的結果基本是一致的，但比不考慮參數模糊隨機性的PEM 法計算結果稍小。由于它慮到了各個力學參數的模糊特性，并對每個力學參數都進行了模糊處理，使參數的信息盡可能大地反映出來，這相對于不考慮其模糊性來說更為合理，也與人們的經驗理解相符合。

5.3 參數k 取值對結果的影響分析

參數k 決定力學參數最大可能計算區間的確定，實質是考慮參數變異性從點的試驗值到單元的計算值的局部平均化影響。可以根據試驗參數統計或人們的經驗來確定。k 值大小受參數變異性、空間相關程度、樣本數大小等影響。不同情形下邊坡的可靠性分析結果見表5。

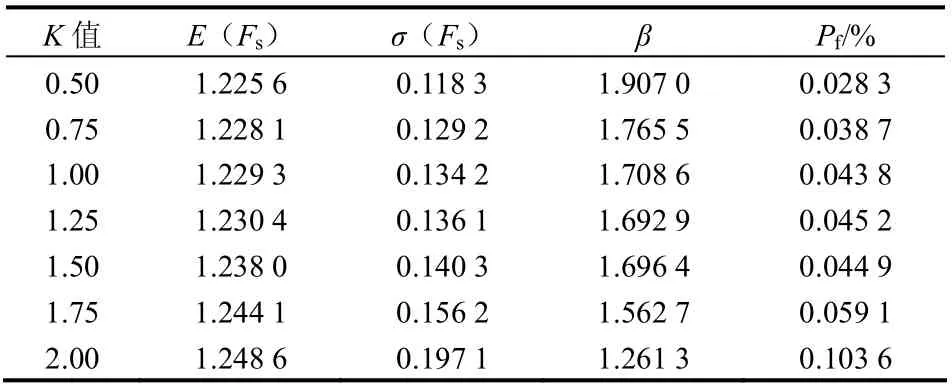
表5 不同k 值的分析結果 Table 5 Analysis results according to different values of k

由表可知，針對不同的k 值，可求得穩定系數的變異系數取值范圍為[0.096～0.158]，邊坡破壞概率隨變異系數的增大而增大，k 值越小，參數的置信度越高，可靠度結果越大。因此，對穩定系數變異性較小的邊坡工程來說，參數的變異性帶來的模糊隨機可靠度變化不明顯，但當穩定系數變異性較大時，應當對加k 的取值進行系統的研究，以免對邊坡的實際工作狀態作出錯誤的評價。

5.4 參數相關性對計算結果的影響分析

考慮力學參數c 和φ 的相關性對可靠性計算結果的影響，當k = 1.5 時，取不同的相關系數進行模糊可靠性計算，計算結果見表6。

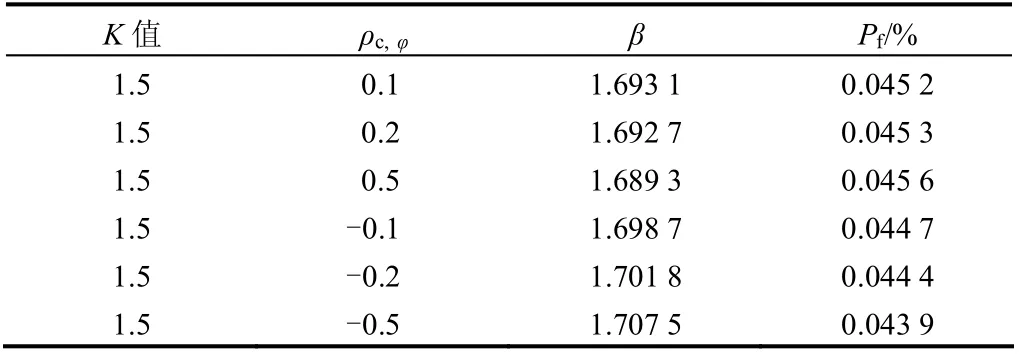
表6 參數相關性對計算結果的影響 Table 6 Effect of correlation on reliability results

表6 計算結果表明，巖土體力學參數的相關性對邊坡模糊隨機可靠性指標的影響并不大。當參數正相關時，隨相關系數的增大，可靠性指標稍有減小；參數負相關時，隨相關系數的增大，可靠性指標稍有增大。

6 結論與建議

本文在統計矩點估計法和模糊隨機理論的基礎上，提出邊坡工程模糊隨機可靠性分析的模糊點估計法；同時，根據邊坡巖土體力學參數的實際近似分布類型，采用正態模糊數對隨機變量進行模糊化處理。該方法不需要構造邊坡極限狀態方程概率密度函數，概念清楚、使用方便、計算效率高，不僅可以計算出穩定系數的均值和標準差，而且可以給出穩定系數和可靠性指標的波動區間，尤其對復雜邊坡和隱式功能函數可靠性分析具有很大的潛力。參數k 的確定比較關鍵，應根據實際經驗和室內試驗對其進行更加全面系統的研究，以便對邊坡的實際狀態作出客觀合理的評價。計算結果表明，邊坡破壞概率為44.9%，處于欠穩定狀態，應對其采取及時有效的支護措施。

[1] DODGAOUDAR G R， VENKATACHALAM G. Reliability analysis of slopes using fuzzy sets theory[J]. Computers and Geotechnics， 2000， 49(2)： 111－122.

[2] GIASI C I， MASI P， CHERUBINI C. Probability and fuzzy reliability analysis of a sample slope near Aliano[J]. Engineering Geology， 2003， (67)： 391－402.

[3] 彭祥. 三峽般閘高邊坡穩定的模糊隨機可靠性分析[D]. 北京： 華北水利水電學院北京研究部， 1997.

[4] 李文秀. 巖土邊坡穩定性的模糊測度分析[J]. 巖土工程學報. 1996， 18(2)： 11－16. LI Wen-xiu. Fuzzy measure analysis for the stability of rock and soil slopes[J]. Chinese Journal of Geotechnical Engineering， 1996， 18(2)： 11－16.

[5] 李彰明. 模糊分析在邊坡穩定性評價中的應用[J]. 巖石力學與工程學報， 1997， 16(5)： 491－495. LI Zhang-ming. Application of fuzzy analysis in slope stability evaluation[J]. Chinese Journal of Rock Mechanics and Engineering， 1997， 16(5)： 491－495.

[6] 譚曉慧. 邊坡穩定分析的模糊概率法[J]. 合肥工業大學學報(白然科學版)， 2001， 24(3)： 443－446. TAN Xiao-hui. The stability analysis of slope by fuzzy probability method[J]. Journal of Hefei University of Technology， 2001， 24(3)： 443－446.

[7] 樓芬， 鄧建. AHP-Fuzzy 法在露天礦邊坡穩定性分析中的應用[J]. 采礦技術， 2008， 8(2)： 28－30.

[8] 羅文強， 龔玨. Rosenblueth 方法在斜坡穩定性概率評價中的應用[J]. 巖石力學與工程學報， 2003， 22(2)： 232－235. LUO Wen-qiang， GONG Yu. Application of Rosenblueth moment estimation method into probabilistic analysis of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering， 2003， 22(2)： 232－235.

[9] HARR M E. Reliability-based design in civil engineering[M]. New York： McGraw-Hill Companies， 1987.

[10] ZIMMERMANN H J. Fuzzy set theory and its applications[M]. Boston： Kluwer Academic Publishers， 1991.

[11] 賈厚華， 賀懷建. 邊坡穩定模糊隨機可靠度分析[J]. 巖土力學， 2003， 24(4)： 657－660. JIA Hou-hua， HE Huai-jian. Analysis of fuzzy-random reliability of slope stability[J]. Rock and Soil Mechanics， 2003， 24(4)： 657－660.

[12] 譚文輝， 蔡美峰. 邊坡工程廣義可靠性分析[M]. 北京： 科學出版社， 2010.

[13] 楊坤， 周創兵， 張昕， 等. 邊坡塊狀結構巖體模糊隨機可靠性分析[J]. 巖石力學與工程學報， 2006， 25(2)： 408－412. YANG Kun， ZHOU Chuang-bing， ZHANG Xin， et al. Fuzzy-random reliability analysis of blocky rock mass in slopes[J]. Chinese Journal of Rock Mechanics and Engineering， 2006， 25(3)： 408－412.