海堤地基固結系數反演與工后沉降分形模型預測

秦植海，秦 鵬

（浙江水利水電專科學校 建筑工程系，杭州 310018）

1 前 言

海堤是沿海地區由當地土石材料填筑而成，用來防御臺風、抵御海潮的重要水利設施，但我國的海堤工程長期處于缺乏有效監管、維護的狀態，海堤的不均勻沉降引起的堤身破壞對沿海地區人民生命安全和經濟發展構成了巨大安全隱患[1]。近年來隨著相關部門的重視和監測技術的進步，部分地區正在建立或已逐步形成較為系統的海堤沉降監測系統，但沒有合理有效的監測分析，監測系統和監測信息無法真正發揮作用，因此，針對海堤特點的理論分析預測模型研究十分迫切[2]。

目前海堤沉降的監測資料分析、預測主要有兩種方式：（1）通過監測資料時間序列的變化趨勢預測海堤工后沉降的過程，如經驗公式法[3]、Asaoka法[4]、灰色理論[5]等已在該領域得到了應用，但這些模型的參數概念并不清楚，缺乏對土體沉降機制上的認識；（2）對采集的土樣進行室內土工試驗，確定地基土的固結系數后，通過太沙基固結理論推求現場土層沉降過程。由于室內試驗條件與現場土層條件、荷載分布情況存在較大差異，且室內土工試驗受到取土質量、試樣代表性、試驗技術水平及計算方法等各因素的影響，造成室內試驗得到的固結系數與實際情況有較大出入，從而影響海堤沉降預測結果的可信度[6]。

在海堤實測沉降資料基礎上反演計算參數，并以此為依據對后期沉降作出預測，這種反演分析方法能夠全面反映現場各要素綜合影響，反演得到的固結系數即為整個地基的等效固結系數，實用性強，受到了工程界的重視[7]。在過去的研究中，石名雷等[8]針對具有豎向排水體飽和粉砂土基礎沉降問題，進行了固結系數的反演，周健等[9]對分級施加荷載的地基進行了土層參數和固結系數的反演，并進行動態預測，鄧永鋒等[10]則更深入地將Asaoka法與太沙基一維固結理論耦合，對地基土沉降進行了反演預測。然而，目前的反演分析大多是以公路軟土路堤為研究對象，海堤工程具有地質情況復雜、工作環境特殊、修建方法各異的特點，而且由于長期缺乏有效地管理、監測，有效的海堤沉降數據十分有限，因此，針對海堤工程的特殊性對海堤沉降監測資料進行分析具有重要工程實際意義。

本文以浙江省海堤現場工后沉降監測數據為研究對象，運用分層總和法和太沙基一維固結理論對海堤地基土層進行反演，并針對海堤沉降監測數據偏短的特點，嘗試引入非線性動力學中的分形理論分析固結系數時間序列，進一步對沿海地區海堤沉降的工后變化趨勢進行預測。

2 海堤沉降過程分析基本研究路線

海堤的沉降主要包括堤身的壓密變形和地基變形兩部分，前者可以通過改進海堤填料和提高施工壓實度來控制，且在施工期已大部分完成，后期變形基本由填料的塑性變形引起，在海堤沉降中所占比例極小；后者占海堤總沉降的絕大部分，因此，地基固結變形決定了海堤沉降發展的形態[11]。通過對浙江省寧波、溫州、臺州、舟山、嘉興等地區共計34 個海堤（塘）工程地質資料及沉降監測數據進行分析，發現浙江省海堤監測資料具有以下特點：（1）監測主要是以堤頂沉降監測為主，沒有對地基進行分層監測；（2）海堤工程沒有明確的建設管理單位，造成監測數據主要集中在施工期和施工結束后較短時間內，缺乏長期的沉降監測資料。為了能夠有效預測海堤工后長期沉降，提前研判可能發生開裂的堤段，本文建立了海堤沉降過程預測方法，分以下4 個步驟：

（1）以海堤的前期巖土工程勘察及設計資料為依據，利用分層總和法計算海堤最終沉降量，力求在沉降反演中體現地基各層土體的特性；

（2）通過簡化土層參數的思想推導海堤的固結系數反演公式，利用海堤沉降監測數據反演計算固結系數；

（3）對固結系數的變化規律進行總結、分析，并在該領域引入具有自相似性的分形模型對具有特殊變化規律的小數據量固結系數序列進行預測；

（4）根據計算得到的地基最終沉降量及固結系數預測時間序列，推求海堤沉降變化趨勢，并以工后沉降短期監測值對預測結果加以驗證。

3 海堤沉降監測數據的固結系數反演及規律分析

3.1 海堤沉降監測數據的固結系數反演

本文選取施工結束后的監測數據為研究對象，基于分層總和法和太沙基一維固結理論反演該時段的土體固結系數時間序列。海堤沉降監測數據反演主要有以下兩個步驟：

（1）分層總和法計算地基最終沉降量

假設地基土是線彈性體，沒有側向膨脹，且土中水及土粒本身的壓縮量忽略不計。在外荷載作用下變形只發生在有限厚度的范圍內（壓縮層）[12]，用分層總和法計算得到地基的最終沉降量tS 。

（2）海堤沉降的固結系數反演

設土體完全飽和，土顆粒和孔隙水不可壓縮，單元土體的體積壓縮量等于單元體流量之差，根據太沙基一維固結微分方程和豎向固結度計算公式，積分運算可化簡得到固結度公式為

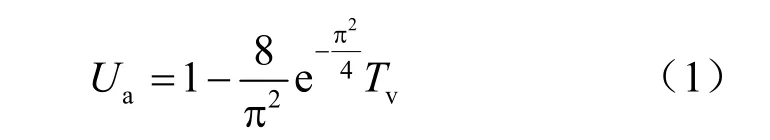
整理可得到固結系數：

將現場監測的海堤沉降值tS 對應的固結度代入式（2），可反演得到土層的固結系數。

3.2 固結系數規律分析

固結系數vC 作為海堤沉降的關鍵土工參數，其大小反應了土的壓縮性和滲透性，與土的礦物成分和粒度成分有密切的關系，因此，不同監測階段、不同監測時期得到的固結系數具有很大的差異性。通過推求的固結系數反演公式，對浙江省34 項海堤工程工后沉降數據反演得到的固結系數時間序列進行歸類分析發現，固結系數與時間的變化規律大致有以下兩種類型：

（1）固結系數隨時間增長震蕩后趨于收斂。這種類型的數值主要出現在工程結束較長時間后，在文獻中一般采用取均值的方法進行計算[7]；

（2）固結系數具有較強的規律性，呈逐漸增加或減小的趨勢。這種類型的數值主要出現在施工結束后的較短時間內，由于外部荷載的施加剛剛結束，固結系數還處于一種不穩定的變化狀態。這類固結系數的傳統求解方法仍為取均值，但由于固結系數時間序列呈非線性的變化趨勢，簡單的均值求法勢必會對沉降的預測值造成影響，產生誤差，按固結系數變化趨勢，采用合適的預測模型反演土層實際固結系數，進而進行海堤工后沉降預測十分必要。

由于海堤工程缺乏長期的監測數據，具有較強趨勢性的固結系數時間序列存在長度較短，數據受到白噪干擾的特點，傳統的預測方法如灰色理論、神經網絡等對這一類的數據處理效果并不理想，因此，嘗試引入分形理論對具有趨勢性的固結系數進行分析、預測。在以往的研究中發現，分形理論具有自相似性的特點，能充分挖掘數據本身的信息，對小數據量趨勢性數據具有較強的預測效果[13]。

4 改進變維分形模型在趨勢性固結系數時間序列預測中的應用

分形理論是Mandelbort 于20 世紀70 年代中期創立的，它基于部分與整體的自相似性，直接從非線性復雜系統的本身入手，分析研究對象的自身性質和規律[13]。分形理論的提出，為揭示隱藏于混亂復雜現象中的精細結構和定量地描述系統提供了理論基礎，并在眾多領域得到應用[14]。在過去的研究中發現，巖土體可以被看做復雜的非線性動態系統，分形維數可以定量地對巖土體變形進行描述[15－16]，本文在前人研究的基礎上，嘗試在海堤沉降分析領域引入分形預測模型，對具有較強趨勢性的小數據量固結系數時間序列進行預測，并利用式（1）計算得到海堤工后長期沉降過程曲線，以期對海堤工后的管理、維護工作提供重要的參考依據，提前研判可能發生開裂的堤段，采取預防措施。

4.1 常維分形和變維分形

常用的分形模型主要有常維分形和變維分形兩種。目前應用的常維分形可用如下冪指數分布定義[13]：

式中：r 為特征線度；N 為與r 有關的數量；C 為待定常數；D 為分維數

當D 為常數時，在雙對數坐標上表現為一條直線，可以通過變化求出分維數，即

針對常維分形無法處理雙對數坐標上的非直線函數關系的問題，引入了變維分形的概念，其分維數D 不再是常數，而是特征線度r 的函數[14，17]：

N 與r 之間的任意函數關系 N = f ( r)均可轉化為變維分形的形式[17]，即使 f ( r ) = C / rD，得到變維分形公式為

4.2 海堤工后沉降的改進及變維分形模型建立

由于自然界中嚴格意義上滿足常維分形的現象是不存在的，所以大量數值模型需要用變維分形的方法進行計算，但當數據復雜時，變維分形中的函數式又往往龐大而難于計算。研究證明，對于任意函數關系 N = f ( r)都可以轉換成常維分形N= C / rD的形式，即將數據進行一系列的變換，使變換后的數據能用常維分形處理，即通過構造1 階、2階、3 階……累積和的分段變維分形模型，然后選擇效果最好的變換并確定相應的分形參數[18]，基于此思想，本文利用改進變維分形模型對趨勢性海堤固結系數進行預測，進而反演海堤地基沉降值。該模型的具體建立步驟如下：

（1）將趨勢性固結系數時間序列點( Ni， ri) (i= 1，2，… ，n )繪于雙對數坐標上，將 Ni排成一個基本序列，即

（2）根據基本序列構造其他序列。

按照下面的規則，通過逐階累加的方法構造監測數據的累積和時間序列：

其中， i = 1，2，…， n。

（3）建立各階累積和的變維分形模型。

（4）比較各階累積和變維分形模型，選擇最為平順的累積變換曲線確定分形階數，對選定的分形維數時間序列曲線插值，擬合計算出分形參數[21]。

（5）根據選定的分形維數帶入改進變維分形模型，對固結系數時間序列趨勢項進行預測，將固結 系數預測值代入式（1），即可對海堤沉降的監測數據演化趨勢進行預測。

5 工程實例

為了驗證固結系數反演分析及分形模型預測的可靠性，采用浙江省洞頭縣北岙后二期東圍堤工程的海堤監測數據作為研究對象進行驗證計算。

巖土工程勘察報告顯示，該海堤地基在鉆探深度范圍內共揭示3 個大土層，其中第1 土層可細分為3 個亞層。分布特征詳見表1。

表1 鉆探深度范圍內的土層特征[22] Table 1 Characteristics of soil from different horizons[22]

選取洞頭北岙后二期東圍堤工程0+100 測點2007 年3 月至2008 年12 月間22 個沉降監測數據作為分析對象，此時海堤沉降處于變形發展階段，原始沉降監測數據間隔時間為一個月。取前15 個點作為計算數據，后7 個數據用以檢驗，為方便計算，以監測數據的時間先后進行編號， 1，2，r= …，可以得到海堤沉降時間序列如圖1 所示。結合巖土工程勘察資料，取影響土層的深度為20 m，通過室內壓縮試驗計算得到最終沉降量tS 為500 mm，據式（2）反演得到固結系數時間序列如圖2 所示，可以看到固結系數呈趨勢性增長。

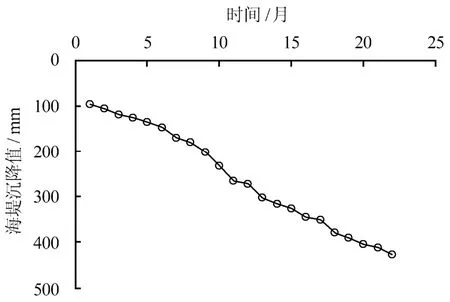
圖1 洞頭北岙后二期東圍堤工程0+100 測點 沉降時間序列 Fig.1 Settlement time series of Beidaihou second east-causeway project in 0+100 monitoring point

圖2 洞頭北岙后二期東圍堤工程0+100 測點 固結系數時間序列 Fig.2 Inversed consolidation coefficient time series of Beidaihou second east-causeway project in 0+100 monitoring point

引入改進變維分形預測模型，對反演得到的固結系數時間序列進行分析。首先根據計算步驟，對時間序列進行1～4 階累積和構造，分別求出固結系數的各階分維值，如表2 所示。

為了便于直觀地分析和選取，將表2 數據繪制于圖3，可以看到 3D 、 4D 系列值擬合效果都比較理想，特別是 3D 曲線在后半段十分平順。因此，本文選取 3D 曲線作為預測模型的分形參數曲線，對曲線的分段分形維數進行擬合、反推，得到模型的趨勢項序列如表3 所示。

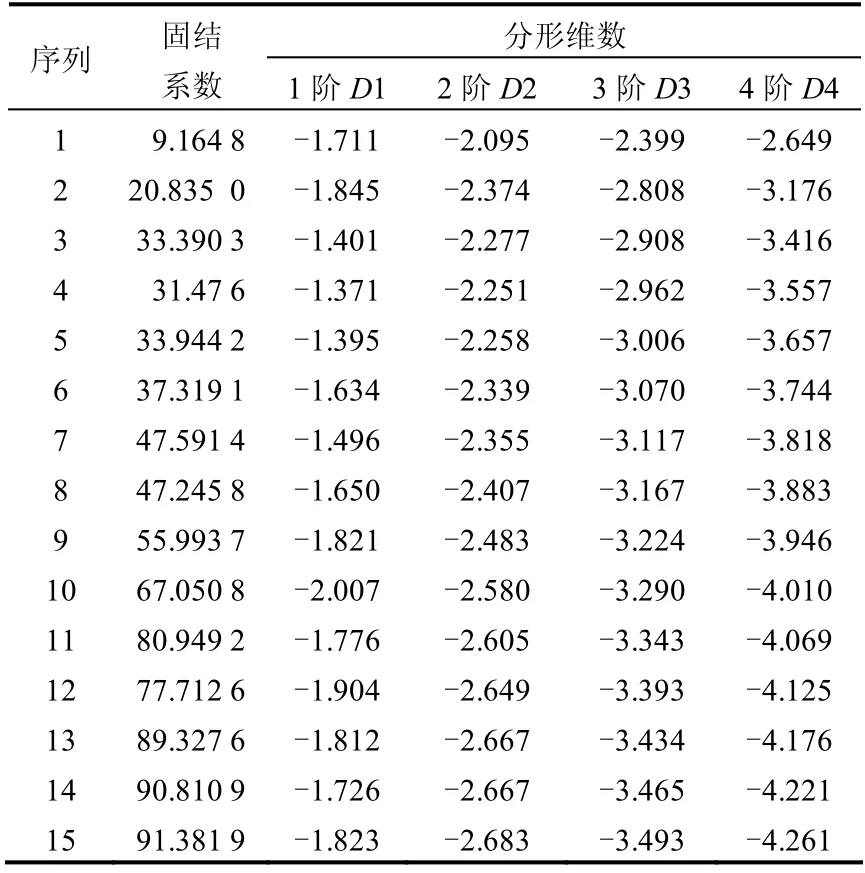
表2 洞頭北岙后二期東圍堤工程0+100 測點固結系數 變維分形維數計算結果 Table 2 Results of n-order variable-dimensional fractal sequences of Beidaihou second east-causeway project in 0+100 monitoring point

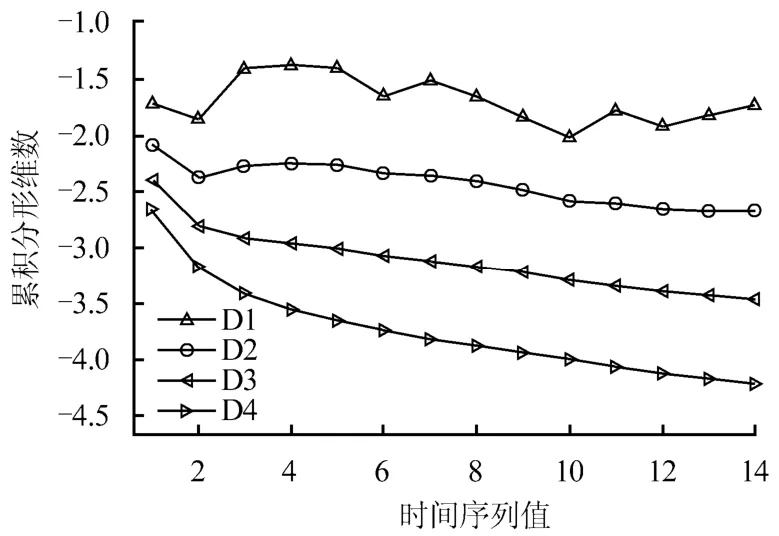
圖3 固結系數各階變維分形維數匯總 Fig.3 N-order variable-dimensional fractal sequences

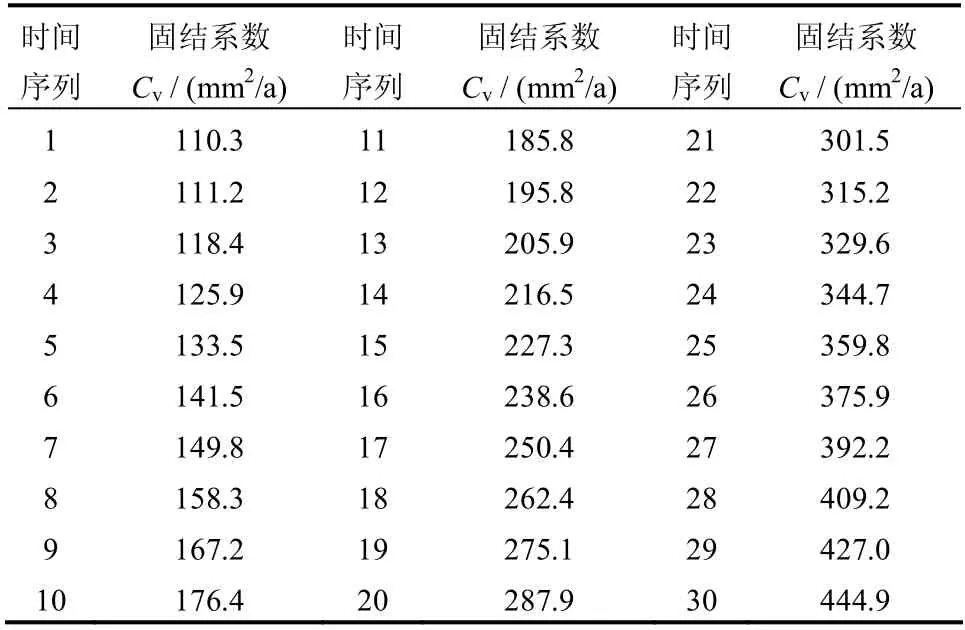
表3 固結系數預測值時間序列 Table 3 The prediction of consolidation coefficients

通過改進變維分形模型可對固結系數的趨勢值進行預測，利用式（1）計算可得到海堤工后短期、長期沉降曲線如圖4、5 所示。由圖4 可以看出，分形模型預測結果與實際觀測結果在工后短期內吻合度較好，由長期沉降預測曲線可以看出，固結變形隨時間增長逐漸完成，本工程工后2 年內土層的固結度接近于1，海堤軟土地基的沉降基本結束，沉降曲線符合土體沉降的變化規律。

圖4 0+100 測點短期沉降預測值與實測值對比曲線 Fig.4 Prediction of short-term settlement in 0+100 monitoring point

圖5 0+100 測點長期沉降預測值與實測值對比曲線 Fig.5 Prediction of long-term settlement in 0+100 monitoring point

5 結 論

（1）以浙江省海堤工程現場采集的短期監測數據為基礎，利用改進變維分形預測模型對土層固結系數進行了分析，并通過預測出的固結系數趨勢項對海堤地基長期沉降過程進行了預測，為海堤工程的工后維護、管理提供了參考依據，與傳統方法相比，該方法反演得到現場土層固結系數并用非線性理論對長期沉降進行預測，避免了由室內試驗得到固結系數的不準確性，又比經驗公式更能反映出實際土體的固結機制，其結果更加真實可信。

（2）針對具體工程，使用本文方法對海堤不同測點的實測沉降數據進行反演、預測，即可得到海堤不同測點的沉降量與時間s-t 關系曲線，進一步可繪制出多條不同測點相同時間n-s 關系線，相鄰測點沉降差較大時，即預示著該時段此處海堤發生開裂的可能較大。通過這種方法就可以做到提前預測、提前處理，達到減小工程隱患的目的。

致謝：特別感謝浙江省圍墾局及浙江省各市縣水利局在本次省水利廳海堤專項課題研究中提供的寶貴現場資料。

[1] 黃銘， 劉俊. 海堤滲壓監測因果模型基本結構和因子選擇[J]. 上海交通大學學報， 2008， 42(11)： 1931－1934. HUANG Ming， LIU Jun. The frame of sea wall osmosis pressure monitoring model and factors selection[J]. Journal of Shanghai Jiaotong University， 2008， 42(11)： 1931－1934.

[2] 潘翔， 黃銘， 王躍威. 海塘滲壓監測分析的時間序列組合模型[J]. 巖土力學， 2006， 27(8)： 1374－1378. PAN Xiang， HUANG Ming， WANG Yue-wei. The time series model of seawall osmotic pressure monitoring analysis[J]. Rock and Soil Mechanics， 2006， 27(8)： 1374－1378.

[3] 包太， 劉新榮， 朱凡， 等. 固結系數的最小二乘法計算[J]. 巖土工程學報， 2005， 27(10)： 1230－1232. BAO Tai， LIU Xin-rong， ZHU Fan， et al. Least square method for the consolidation coefficient evaluation[J]. Chinese Journal of Geotechnical Engineering， 2005， 27(10)： 1230－1232.

[4] 王志亮， 黃景忠， 李永池. 沉降預測中的Asaoka 法應用研究[J]. 巖土力學， 2006， 27(11)： 2025－2032. WANG ZHi-liang， HUANG Jing-zhong， LI Yong-chi. Study on application of Asaoka's method to settlement prediction[J]. Rock and Soil Mechanics， 2006， 27(11)： 2025－2032.

[5] 臧德彥. 灰色系統理論在海堤沉降預測中的應用[J]. 測繪工程， 1999， 8(2)： 50－54. ZANG De-yan. Application of the theory of gray system to forecast the dam subsidence forecasting[J]. Engineering of Surveying and Mapping， 1999， 8(2)： 50－54.

[6] 張儀萍， 張曉海. 室內固結系數的一種推算方法[J]. 巖土工程學報， 2002， 24(5)： 616－618. ZHANG Yi-ping， ZHANG Xiao-hai. A method for evaluating coefficient of consolidation[J]. Chinese Journal of Geotechnical Engineering， 2002， 24(5)： 616－618.

[7] 周健， 閆東霄， 賈敏才， 等. 某深水港土層固結系數反演及工后長期沉降預測[J]. 巖土力學， 2008， 29(5)： 1407－1410. ZHOU Jian， YAN Dong-xiao， JIA Min-cai， et al. Back analysis of consolidation coefficient of soils and prediction of long term post-load settlement of a deep- water port[J]. Rock and Soil Mechanics， 2008， 29(5)： 1407－1410.

[8] 石名磊， 趙俊明， 魯安順. 高速公路地基沉降反演分析[J]. 東南大學學報(自然科學版)， 2005， 5(4)： 589－592. SHI Ming-lei， ZHAO JUN-ming， LU An-shun. Back- calculation of ground settlement for freeway[J]. Journal of Southeast University( Natural Science Edition)， 2005， 5(4)： 589－592.

[9] 周健， 白彥峰， 賈敏才. 某礦石碼頭堆場礦石分級壓載的地基沉降預測[J]. 巖土力學， 2009， 30(7)： 2101－2104. ZHOU Jian， BAI Yan-feng， JIA Min-cai. Prediction of foundation settlement of a heap of ore-port under multi- stage loading during period of use[J]. Rock and Soil Mechanics， 2009， 30(7)： 2101－2104.

[10] 鄧永鋒， 劉松玉， 洪振舜. 基于沉降資料反演固結系數的方法研究[J]. 巖土力學， 2005， 26(11)： 1807－1809. DENG Yong-feng， LIU Song-yu， HONG Zhen-shun. Back analysis of consolidation coefficient with in-situ settlement data[J]. Rock and Soil Mechanics， 2005， 26(11)： 1807－1809.

[11] 章定文， 劉松玉. 試論連云港海相軟土路堤沉降規律[J]. 巖土力學， 2006， 27(2)： 304－308. ZHANG Ding-wen， LIU Song-yu. Settlement features of embankment of Lianyungang marine clay[J]. Rock and Soil Mechanics， 2006， 27(2)： 304－308.

[12] 錢家歡， 殷宗澤. 土工原理與計算[M]. 北京： 中國水利水電出版社， 1996.

[13] MANDELBROT B B. Les objets fractals： Forme， hasard et dimension[M]. Paris： Flammarion， 1975.

[14] MANDELBROT B B， EVERTSZ C J G， JONES P W. Fractals and chaos： The mandelbrot set and beyond[M]. New York： Springer， 2004.

[15] 秦鵬， 秦植海. 基于分形理論的巖質高邊坡監測資料分析[J]. 水利水運工程學報， 2008， 9(3)： 92－97. QIN Peng， QIN Zhi-hai. Analysis of high rocky slope monitoring data based on fractal theory[J]. Hydro-Science and Engineering， 2008， 9(3)： 92－97.

[16] 薛天放， 楊慶， 欒茂田. 基于GIS 技術的滑坡空間分布的分形特征研究[J]. 巖土力學， 2007， 28(2)： 347－354. XUE Tian-fang， YANG Qing， LUAN Mao-tian. Research on fractal characters of spatial distribution of landslide based on GIS[J]. Rock and Soil Mechanics， 2007， 28(2)： 347－354.

[17] MANDELBROT B B. Fractal analysis and synthesis of fracture surface roughness and related forms of complexity and disorder[J]. International Journal of Fracture， 2006， 138， 13－17.

[18] 付昱華. 變換形成的分形與海洋環境數據分析預測[J].海洋通報， 2000， 19(1)： 79－88. FU Yu-hua. Transform-formed fractals and analyses and forecast of marine environment data[J]. Marine Science Bulleten， 2000， 19(1)： 79－88.

[19] 秦鵬. 基于非線性理論的高邊坡監測數據分析與預測[D]. 合肥： 合肥工業大學， 2009.

[20] 秦鵬， 秦植海. 巖質高邊坡監測數據的改進變維分形預測模型[J]. 水利水運工程學報， 2010， 3(1)： 90－94. QIN Peng， QIN Zhi-hai. Forecasting model of monitoring data of rock high slope based on improved variable dimension fractal theory[J]. Hydro-Science and Engineering， 2010， 3(1)： 90－94.

[21] 秦鵬，張喆瑜，秦植海等.滑坡體監測數據的改進變維分形-人工神經網絡耦合預測模型[J].長江科學院院報， 2012， 29(3)： 29－34. QIN Peng， ZHANG Zhe-yu， QIN Zhi-hai， et al. IVDFANN prediction model on monitoring data of landslide deformation[J]. Journal of Yangtze River Scientific Research Institute， 2012， 29(3)： 29－34.

[22] 秦植海， 秦鵬， 方榮. 浙江省典型海堤工后沉降分析報告[R]. 杭州： 浙江省圍墾技術中心， 浙江水利水電專科學校， 2009.