不含 3-圈平面圖的線性染色＊

王 侃

(浙江師范大學數理與信息工程學院,浙江金華 321004)

0 引 言

本文所考慮的圖都是簡單圖.用 V(G),E(G),Δ(G)和δ(G)分別表示圖 G的頂點集、邊集、最大度和最小度.G的圍長 g(G)是指 G中最短圈的長度.

圖 G的一個正常染色是從頂點集合 V(G)到顏色集合{1,2,…,k}的一個映射,使得任意 2個相鄰的頂點染不同的顏色;圖G的一個線性 k-染色是一個正常染色,使得染任意 2種顏色的頂點集合導出的子圖是一些點不交的路的并;圖 G的線性色數 lc(G)定義為 G的所有線性 k-染色中最小的 k值.

文獻[1]首先研究了圖的線性染色,證明了任意圖 G的線性色數滿足圈染色是 G的一個正常染色,使得染任意 2種顏色的頂點集合導出的子圖是一個森林.無圈染色的概念是由 Grünbaum[2]提出的.這方面的研究可參閱文獻[2-5].

2008年,Esperet等[6]把線性染色的概念推廣到線性選擇性,他們研究了樹、格子圖、完全二部圖、平面圖、外平面圖、最大度為 3或 4的圖以及有較小最大平均度的圖的線性選擇數.

定理 1[6]設 G是一個平面圖,則

定理 2[7]設 G是一個平面圖,則

1)若存在一個有序對 (Δ,g)∈{(13,7),(7,9),(5,11),(3,13)},使得Δ(G)≥Δ,g(G)≥g,那么

本文考慮圍長至少為 4的平面圖的線性染色,得到如下的結果:

定理 4 設M≥5是一個正整數,G是一個Δ(G)≤M且沒有 3-圈的平面圖,則

1 基本概念

對于一個平面圖 G,用 F(G)表示它的面集合.對?f∈F(G),若 u1,u2,…,un是 f邊界上依序排列的頂點,則記 f=[u1u2…un],注意到點的重復出現是允許的.面的度是指它的邊界上邊的條數,其中割邊被計算 2次.對?x∈V(G)∪F(G),用 dG(x)表示 G中 x的度.在不產生混淆的情況下,可以用 d(x)代替 dG(x).一個度數為 k的頂點 (面)被稱為 k-點 (k-面),一個度數至少為 k或至多為 k的頂點 (面)被稱為 k+-點 (k+-面 )或 k--點 (k--面 ).用 NG(v)表示 G中 v的鄰點的集合.

設 c是 G的一個部分線性染色,顏色集合為 C.對?v∈V(G),用 C2(v)表示 C中正好在NG(v)上出現 2次的顏色子集合;對任意的頂點集合 T,用 C2＊(T)表示 C中至少在 T上出現 2次的顏色子集合.為了討論方便,對 i=1,2,3,稱恰關聯 i個 4-面的 3-點為類型 i的,且稱關聯至多 1個 4-面的 3-點為好 3-點,關聯至少 2個 4-面的 3-點為壞 3-點.

2 極小反例的性質

假設定理 4不成立.設 G是一個極小反例,即 G是一個沒有 3-圈的平面圖,滿足Δ(G)≤M,且以下性質:

斷言 1 δ(G)≥3.

證明 假設 G包含 1-點 v與某點 u相鄰.顯然,H=G-{v}是一個沒有 3-圈的平面圖,滿足Δ(H)≤Δ(G).由 G的極小性知,H有一個線性染色 c應用顏色集合 C.為將 c擴充到整個圖 G,用不在 C2(u)∪

假設 G包含一個 2-點 v,其鄰點為 x,y.顯然,H=G-{v}是一個沒有 3-圈的平面圖,滿足Δ(H)≤Δ(G).由G的極小性知,H有一個線性染色c應用顏色集合C.用不在{c(x),c(y)}∪C＊2(NH(x)∪好 v.與 G的選擇矛盾!斷言 1證畢.

斷言 2 G沒有相鄰 3-點.

證明 假設 G包含一條路 P=v1v2v3v4,使 d(vi)=3(i=2,3).ui-1是 vi的不同于 vi-1,vi+1(i=2,3)的鄰點,如圖 1所示.

顯然,H=G-{v2}是一個沒有 3-圈的平面圖,滿足Δ(H)≤Δ(G).由 G的極小性可得,H有一個線性染色 c應用顏色集合 C.若 c(u1),c(v1),c(v3)不全相同,則 v2的禁用顏色為{c(u1),c(v1),c(v3)}∪C＊2(NH(u1)∪NH(v1)∪NH(v3)).因|{c(u1),c(v1),c(v3)}|+5),故能用C中的顏色染v2.若c(u1)=c(v1)=c(v3),則用C({c(v1),c(v4),c(u2)}∪C＊2(NH(v4)∪NH(u2){v3}))中的顏色 a改染 v3.因 |{c(v1),c(v4),c(u2)}|+|C＊2(NH(v4)∪NH(u2){v3})|≤3+

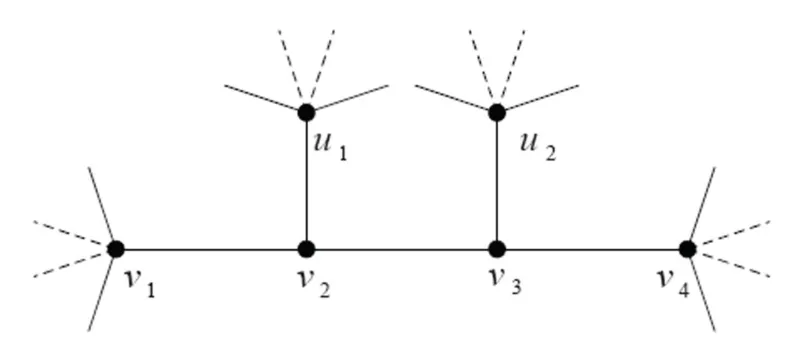
圖 1 斷言 2中的子結構

斷言 4 設 x1是和一個 4-面 f關聯的 3-點,則 x1的 2個和 f關聯的鄰點一定是 5+-點.

證明 假設 G包含這樣一個面 f=[x1x2x3x4],滿足 d(x1)=3,d(x2)≤4.由斷言 1和斷言 2知,d(x2)=4.記 y1是 x1的不同于 x2和 x4的鄰點;xj2(j=1,2)是 x2的不同于 x1和 x3的鄰點,如圖 2所示.

圖 2 斷言 4中的子結構

圖 3 斷言 5中的子結構

斷言 5 不存在一個 5-點和 5個壞 3-點相鄰.

證明 假設 G包含這樣的一個 5-點 v,它的鄰點 x1,x2,x3,x4,x5全是壞 3-點,則和 v關聯的面中一定有 2個相鄰 4-面,設為 f1=[vx1y1x2],f2=[vx5y2x1],如圖 3所示.

顯然,H=G-{x1}是一個沒有 3-圈的平面圖,滿足Δ(H)≤Δ(G).由 G的極小性可得,H有一個線性染色 c應用顏色集合 C.考慮下面 2種情形染 x1:

1)c(y1),c(y2),c(v)不全相同.

用不在{c(y1),c(y2),c(v)}和C＊2(NH(y1)∪NH(y2)∪NH(v))中的顏色染x1,x1的禁用顏色數至

2)c(y1)=c(y2)=c(v).

用不在{c(y1),c(x2),c(x3),c(x4),c(x5)}和 C＊2(NH(x2)∪NH(x3)∪NH(x4)∪NH(x5){v,y1,(M≥5),所以可以用 C中的顏色染好 x1.斷言 5證畢.

斷言 6 不存在一個 5-點和至少 3個類型 3的 3-點相鄰.

證明 假設 G包含這樣一個 5-點 v,它的鄰點中至少有 3個是類型 3的 3-點,則至少有 2個類型 3的 3-點是和 v關聯于同一 4-面的.不失一般性,設 x1,x2,x3,x4,x5是 v的鄰點,且 x1,x2都是類型 3的 3-點,x3,x4,x5中至少有 1個是類型 3的 3-點,則和 vx1,vx2關聯的 3個面都是 4-面,設為 f1=[vx1y1x2],f2=[vx5y2x1],f3=[vx2y3x3],如圖 4所示.

顯然,H=G-{x1}是一個沒有 3-圈的平面圖,滿足Δ(H)≤Δ(G).由 G的極小性可得,H有一個線性染色 c應用顏色集合 C.考慮用以下 2種情形染 x1:

1)c(y1),c(y2),c(v)不全相同.

3 定理 4的證明

設 G是定理 4的一個極小反例,為完成證明,應用權轉移方法.首先,結合歐拉公式 |V(G)|-

定義初始權函數 w:對 v∈V(G),令 w(v)=d(v)-4;對 f∈F(G),令 w(f)=d(f)-4.由式 (1)得總的權和為 -8.然后定義一個權轉移規則,且在所有的點和面上執行.一旦權轉移結束,就會產生一個新的權函數 w′.

在整個權轉移過程中權和是不變的,但對于所有的 x∈V(G)∪F(G),有 w′(x)≥0.這就導致了下面一個很明顯的矛盾,因此這樣的反例 G是不存在的:

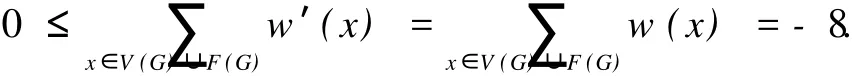
權轉移規則如下:

若 d(v)=4,則 w′(v)=w(v)=d(v)-4=0.

4 結 論

由定理 4立即推出下面結果:

[1]Yuster R.Linear coloring of graphs[J].DiscreteMath,1998,185(1/2/3):293-297.

[2]Grünbaum B.Acyclic colorings of planar graphs[J].Israel J Math,1973,14(4):390-408.

[3]Borodin O V.On acyclic colorings of planar graphs[J].DiscreteMath,1979,25(3):211-236.

[4]Kostochka A V.Acyclic 6-coloring of planar graphs[J].MetodyDiskretAnal,1976,28:40-56.

[5]Mitchem J.Every planar graph has an acyclic 8-coloring[J].DukeMath J,1974,41(1):177-181.

[6]EsperetL,MontassierM,Raspaud A.Linear choosability of graphs[J].DiscreteMath,2008,308(17):3938-3950.

[7]Raspaud A,WangW.Linear coloring of planar graphswith large girth[J].DiscreteMath,2009,309(18):5678-5686.

[8]Li Chao,WangWeifan,Raspaud A.Upper bounds on the linear chromatic number of a graph[J].DiscreteMath,2011,311(4):232-238.