復合二項分布下多險種的負風險模型

趙 娟，金燕生，劉征福

(燕山大學 理學院 河北 秦皇島 066004)

復合二項分布下多險種的負風險模型

趙 娟，金燕生，劉征福

(燕山大學 理學院 河北 秦皇島 066004)

考慮了離散的復合二項分布下多險種的負風險模型.其中，保險公司的保費收入是一個負的常數，并且索賠過程為復合二項過程模型的多險種風險過程.通過構建有關索賠過程的期望方程給出了調節系數的定義，并通過鞅論得到了破產概率的Lundberg不等式(倫德伯格不等式)，運用更新理論與遞歸的手法獲得了破產概率的關系式以及破產概率確切的表達式.而且，最后根據破產概率的具體表達式給出了關于破產概率的一個極限值.

負風險； 復合二項風險過程； 破產概率； Lundberg不等式

0 引言

在經典的復合二項過程中,保險公司單位時間的保費收入為一個常數.文獻[1]給出了u=0的破產概率與一些u≥0的破產概率的計算公式.近年來，越來越多的學者開始關注負風險的情況，如文獻[2-5].其中，生命年金或養老保險就是最典型的例子.文獻[2]中的風險過程為相依的負風險的和,并對比結果研究了相互獨立的險種之間是如何影響破產概率的.雖然這些離散的保險風險模型考慮了負風險過程,并最后得出了破產概率的計算公式和Lundberg不等式,但他們僅僅是研究了單險種的風險模型，而且在文獻[5]中，各個時期保險代理人對投保人支付的年金為1單位元.

我們考慮的多險種負風險模型中,保險人的保費收入是一個負的常數，并且索賠過程為復合二項過程的模型.

1 復合二項分布下多險種負風險模型

復合二項分布下多險種的負風險模型是一個離散的過程,

并且它滿足

(a)R(n)是保險人在第n個時期末初始準備金為u的盈余，u≥0.

(b)保險公司在每個周期向投保人支付年金c單位元，c是一個大于零的常數.

(c)m重險種在每個時期發生索賠的概率分別為p(1),p(2),…,p(m),而且不會發生索賠的概率分別為q(1)=1-p(1),q(2)=1-p(2),…,q(m)=1-p(m),m=1,2,….

(d)索賠序列{Xi(1)}i≥1,{Xi(2)}i≥1,…,{Xi(m)}i≥1分別為獨立同分布的正隨機變量序列，它們的概率分布分別為

pk(1)=P(X(1)=k),pk(2)=P(X(2)=k), …,pk(m)=P(X(m)=k),k=1,2,…，

均值分別為μ1=E(X(1)),μ2=E(X(2)),…,μm=E(X(m)).

而且索賠序列{Xi(1)}i≥1,{Xi(2)}i≥1,…,{Xi(m)}i≥1與復合二項過程{N1(n);n=0,1,2,…},{N2(n);n=0,1,2,…,},…,{Nm(n);n=0,1,2,…},m=1,2,…，相互獨立.

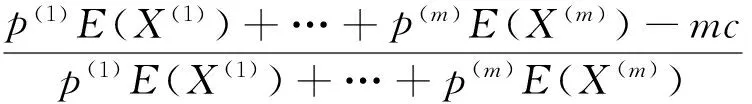
Tu=inf{n≥0|R(n)=u+X(n)<0}表示初始準備金為u的破產時刻，

ψ(u)=P(Tu<∞)表示初始準備金為u的破產概率,則生存概率為?(u)=1-ψ(u).

2 主要結果

定理1對復合二項分布下m重險種的負風險過程{R(n)=u+X(n),n=0,1,2,…}，存在g(r)使得

E[exp(-rX(n))]=exp(ng(r)).

證明{Xi(1)}i≥1，{Xi(2)}i≥1，…，{xi(m)}i≥1均為獨立同分布的隨機變量序列而且與復合二項過程{N1(n);n=0,1,2,…}，{N2(n);n=0,1,2,…}，…，{Nm(n);n=0,1,2,…}，m=1,2,…，相互獨立.所以對于n=0,1,2,…；m=1,2,…,

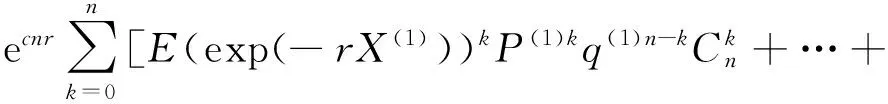
E(exp(-rX(m)))kP(m)kq(m)n-kCnk].

令

則E[exp(-rX(n))]=exp(ng(r))，即證.

由于

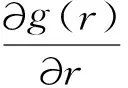
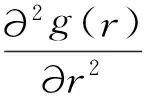
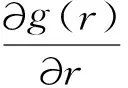
定義1對復合二項過程的m重險種的負風險過程{X(n);n=0,1,2,…}，F={Fn;n=0,1,2,…}稱為濾波，如果Fn=δ{X(m);m≤n}.

如果{T≤n}∈{Fn}，n≥0，隨機變量T∶Ω→[0,∞)是一個停時.

引理1復合二項分布下m重負風險過程中，破產概率滿足Lundberg不等式：ψ(u)≤e-Ru，其中R=sup{r>0;g(r)≤0}稱為Lundberg上界，并且當m=1時R=R0.

證明根據定義Tu是一個停時.對任意的n0<∞,則n0∧Tu是一個停時.由定理1有：?m≤n，

e-ru=Mu(0)=E[Mu(n0∧Tu)]=E[Mu(n0∧Tu)|Tu≤n0]P{Tu≤n0}+

E[Mu(n0∧Tu)|Tu≥n0]P{Tu≥n0}

≥E[Mu(Tu)|Tu≤n0]P{Tu≤n0}.

(1)

顯然，在{Tu<∞}上,R(Tu)=u+X(Tu)≤0.因此，由(1)式，我們可得

從而可得

可見，以上結論是對c=1，m=1的情況[5]的一個推廣.同理，以下引理亦然.

引理2在復合二項分布下m重險種的負風險過程中，令j，k為兩個正變量且0≤k≤j，那么：

(i)ψ(j)=ψ(k)ψ(j-k-1);

(ii)ψ(n)=ψn+1(0).

證明(i)對?0≤k≤j，

ψ(j)=P(j+X(n)<0,?n≥0)

=P(j+X(n)<0,?n≥0|k+X(m)<0,?m>0)P(k+X(m)<0,?m>0)

+P(j+X(n)<0,?n≥0|k+X(m)≥0,?m>0)P(k+X(m)≥0,?m>0)

=P(j+X(n′)=-1,?n′≥0|k+X(m′)=-1,?m′>0)P(k+X(m′)=-1,?m′>0)+0

=P(j-k-1+X(n′-m′)=-1,?n′,m′≥0)P(k+X(m′)=-1,?m′>0)

=ψ(j-k-1)ψ(k).

(ii)由(i)，很容易地可得ψ(1)=ψ2(0)，由歸納假設，則ψ(n)=ψn+1(0).

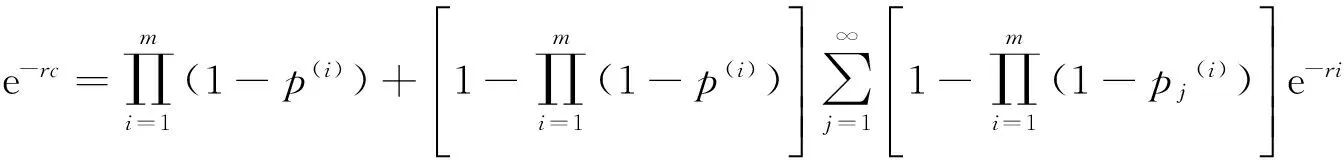
證明根據引理2的(ii)，則ψ(j)=ψj+1(0)，那么ψ(j)=e(j+1)ln ψ(0).令r=-lnψ(0)，可得

ψ(j)=e-r(j+1),ψ(0)=e-r.

(2)

在m重險種的負風險過程

中，當初始準備金為j，j=1,2,…，如果在第一個時期沒有索賠發生，準備金變為j-c，如果在第一個時期發生了索賠量為x的索賠，準備金變為j-c+x.因此，由全概率公式可得

(3)

將(2)式代入 (3)式，得

(4)

將(4)化簡整理，得

(5)

從而由(5)式我們得到一個正解R，因此我們有ψ(j)=e-R(j+1)，且ψ(0)=e-R.

當m=1時，式(5)的正解R是唯一的，并且與定理1中的R0相等.

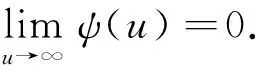
[1] 龔日朝，楊向群．復合二項風險模型的破產概率[J]．經濟數學，2001， 18(2)：95-99．

[2] 董迎輝，王過京．相關負風險和的模型的概率[J]．應用概率統計， 2004， 20(3)： 301-306．

[3] 趙朋，馬松林．雙負二項風險模型的破產概率[J]．合肥學院學報， 2007， 17(1)： 21-23．

[4] 趙培臣，王志攀，張春梅，等．雙復合負二項風險模型的破產概率[J]．廣西大學學報： 自然科學版，2007，32(z1)：69-71．

[5] Luo Kui，Hu Yijun．The negative risk model with the compound binomial process[J]．Journal of Math, 2009, 29(4)：309-412．

NegativeMultipleLineRiskModelwithCompoundBinomialProcess

ZHAO Juan, JIN Yan-sheng, LIU Zheng-fu

(CollegeofSciences,YanshanUniversity,Qinhuangdao066004,China)

The negative multiple line risk model of discrete process was considered.Insurers’ premium income was a negative constant, and claims models were compound binomial risk process.By constructing the expectations about claim process, the adjustment coefficient of definition was given. Then in line with martingale theory, the Lundberg inequality of ruin probability was concluded, furthermore,ruin probability formula and the exact formula of ruin probability were obtained by the updated theory and recursion. And the limit of ruin probability was given at the end of the paper according to the exact formula of ruin probability.

negative risk； compound binomial process； ruin probability； Lundberg inequality

O 211.9

A

1671-6841(2011)03-0034-04

2010-04-28

河北省教育廳自然科學研究項目，編號Z2008136.

趙娟(1984-)，女，碩士研究生，主要從事保險精算研究，E-mail: juanz-84@163.com.