一類二元時滯神經網絡模型同步解的周期性
郭美珍 張 瑗 盧金平
(1.湖南科技學院 計算機系,湖南 永州 425100;2.長沙理工大學 數學與計算科學學院,湖南 長沙 410076;3.湖南大學 數學與計量經濟學院,湖南 長沙 410082)
一類二元時滯神經網絡模型同步解的周期性
郭美珍1張 瑗2盧金平3
(1.湖南科技學院 計算機系,湖南 永州 425100;2.長沙理工大學 數學與計算科學學院,湖南 長沙 410076;3.湖南大學 數學與計量經濟學院,湖南 長沙 410082)
本文對一類二元時滯神經網絡模型的同步解進行定性研究,主要是針對網絡參數的不同取值,分步地求解一個在一定初始函數空間中給定初始值的泛函微分方程,再討論模型同步解的周期性。分析表明網絡參數在神經網絡模型研究中具有極其重要的作用。
神經網絡;同步解;時滯;周期性
1 引 言
國際上從20世紀80年代掀起了人工神經網絡研究的熱潮,至今已經取得了許多優秀的成果,如文獻[1-8]。在上述文獻中,作者討論了幾類二元時滯神經網絡模型(具體模型請參閱所提供的文獻)的動力學行為,涉及的內容有周期解、解的收斂性、同步周期軌道的全局吸引性等。
本文將討論如下二元時滯神經網絡模型

同步解的周期性。這里, )(tx與)(ty分別表示兩個神經元的活躍水平;0>為給定常數,表示反饋時滯;),0[:+∞→Rf表示 )(tx 與 )(ty 的信號傳輸函數;另外,考慮到一個神經元接受另一個神經元的反饋信息的活躍水平的變化還與自身的狀態有關,下面還引入了一個函數[ξ]+:R→[0,+∞)。函數 f、 [ξ ]+分別定義如下

其中 > 0為激勵常數, 0 < a 設X=C([ ? τ,0];R2)為相空間,這是一個由從[?,0]到R2上的連續映射構成的Banach空間, 所賦予的范數為上確界范數。對每個給定的初值 Φ =(?,φ)T∈X (T定義為轉置),在區間[0,],[,2],上可以逐個求解系統(1), 得到唯一的映射 ( xΦ,yΦ)T:[?τ,+∞)→R2使得由此便確定了系統(1)在t≥? 上的唯一解(xΦ(t ),yΦ(t))T。對以任意的 Φ =(?,φ)T∈X為初值的系統(1)的解(xΦ(t ),yΦ(t ))T在t≥0時是連續的和t>0時是幾乎處處可微的[2]。為了討論方便, 以下記 ( x(t),y(t))T=(xΦ(t ),yΦ(t ))T表示系統(1)具有初值 Φ =(?,φ)T∈X的解。 在本文中, 將考慮系統(1)的初值 Φ =(?,φ)T在某個 Rij或Rij中且 (0)= (0)的解 ( x(t ),y(t ))T。此時, 對?t≥0有 x ( t ) ≡ y(t), 稱這種解為同步解. 顯然同步解可由下列單個方程來描述 本節將討論系統(1)同步解的周期性, 即討論系統(2)解的周期性。 定義 若存在某個T>0 和t?>0 使得系統(1)具有初值Φ的解 ( x ( t ),y(t ))T滿足(x(t),y(t))T=(x(t +T),y(t+T))T對任意的 t ≥ t?成立, 則稱 ( x ( t ),y(t ))T為系統(1)的終于T-周期解。 引理[3]對于系統(1), 若 (0 )>0,(0)>0, 則在 [ 0 ,+∞ ) 上恒有 x ( t ) >0, y ( t ) >0。 證明 下面僅證 ∈(b,+∞)的情形, 對于 ∈[a,b]的情形定理的證明類似于 ∈(b,+∞)的情形定理的證明, 故略去。 由于 ∈(b,+∞),故在[0,]上, x(t)滿足如下系統 由定理條件及(4)式知:在 [0 ,]上,x ( t)是嚴格單調遞減的, 且有 x (t)=?(0 ) e?t>be?t>0且 (0)>b,lim ? (0)e?t=0, t→+∞故必存在一點t1使得x(t1)=b且x(t)>b,?t∈[0,t1)。 在 [0 ,t + ]上, x ( t)滿足系統(3)且有解(4), x( t)是嚴格單調遞減的。解得 1 類似于前面的討論可知:存在 t2>t1+使得 x ( t ) ∈ [ a,b], ? t∈ [t1+,t2]且 x ( t2) =b。 在[t1+ ,t2+]上, x ( t)滿足如下系統 且有解 由定 理 條 件及(6)式 知:在 [ t1+ ,t2+]上, x ( t)是 嚴 格單 調 遞 增的, 且 有 x( t ) >b, ? t ∈ (t2, t2+]。 解 類似于前面的討論可知:存在+>23tt使得btx>)(,),(32ttt∈?且btx=)(3。 在[t2+ ,t3+]上, x ( t )滿足系統(3), 且有解 由(7)知:在 [ t2+ ,t3+]上, x ( t)是嚴格單調遞減的,解 對于3tt≥ ,重復上述討論過程,可以發現)(tx是周期的,且周期為 注記 由于對于],[ba∈(意指對一切]0,[?∈t有],[)(bat∈), 當)(tx嚴格單調遞增進入b>的區域時, 總可以找到某個0*>T, 使得系統(2)的解對],(**τ+∈TTt有btx>)(成立, 這樣在討論系統(2)具有初值],[ba∈或),(+∞∈b的解時, 只需考慮),(+∞∈b的情形即可。 基于定理1及注記, 因此不加證明介紹如下定理 則系統(2)具有初值 的解 )(tx 是終于T-周期的, 且周期 證明 下面僅證),(+∞∈b的情形, 對于],[ba∈的情形定理的證明類似于),(+∞∈b的情形定理的證明, 故略去。 x( t)在 [ 0 ,t1+]上的討論完全類似于定理1的討論,這里 即:],[)(batx∈,],[11+∈?ttt。 類似于定理1的討論可知:存在 t2>t1+使得 x ( t ) ∈ [ a,b], ? t∈ [t1+,t2]且 x ( t2) =b。在[t1+ ,t2+]上, x ( t)滿足如下系統 且有解 x (t )= t ?t1?τ+ be?τ(9) 由定理條件及(9)式知:在 [t1+ τ , t2+τ]上, x ( t)是嚴格單調遞增的, 且有 x (t ) > b ,?t∈(t2, t2+]。 解b=x(t2)=t2?t1?τ+ be?τ得 從而由(9)式知: x ( t2+ )=b +。 類似于定理1的討論可知:存在t3>t2+使得x(t)>b,?t∈(t2,t3)且x(t3)=b。 在[t2+ ,t3+]上, x ( t)滿足系統(3), 且有解 由(10)知:在 [t + ,t+]上, x ( t)是嚴格單調遞減的,解 b =x(t)=(b+τ)e?(t3?t2?τ)得 233 本文討論了動力系統模型(1)的同步解(即系統(2)的解)的周期性。 證明了在一定初始函數空間X 中給定初值Φ=(?,φ)T使 ?a、 ?b、 ?a和 ?b 在[?,0]上不變號, 只要初值(?,φ)T及網絡參數 、a、b及 滿足一定的條件, 則系統(1)的同步解(即系統(2)的解)是周期的。 本文的結果顯示了網絡參數 、a、b及 在神經網絡模型(1)研究中的重要性。 [1]喬琛,徐宗本.局部域反饋神經網絡的全局收斂性[J].應用數學學報,2009,(03):536-545 [2]Wu J H. Introduction to neural dynamics and signal transmission delay[M]. Berlin, New York: Walterde Gruyter,2001,115-138. [3]盧金平,黃立宏.一類二元時滯神經網絡模型解的收斂性[J].湖南大學學報,2006,33(6):130-132 [4]Guo S J, Huang L H, Wu J H. Global attractivity of a synchronized periodic orbit in a delayed net-work[J].J.Math.Anal. Appl.,2003, 281 : 620-632. [5]Zhu H Y, Huang L H. Convergence of neural network of two neurons[J]. Journal of Basic Science and Engineering, 2003, 11(2):113-121. [6]Huang L H, Wu J H. Dynamics of inhibitory neural networks with threshold nonlinearity[J]. Fields Institute Communications,2001,29:235-243. [7]Meng Y M, Huang L H. Convergence of solutions of a class of two-neuron bi-threshold neural network model[J]. Fuzzy Systems and Mathematics,2001,15(4):100-104. [8]Meng Y M,Huang L H.Two-neuron bi-threshold neural network dynamical systems with delayed McCulloch-Pitts signal[D].Changsha: College of Mathematics and Econometrics, Hunan University,1999,1-45. TP183;O175.14 A 1673-2219(2011)12-0009-04 2011-01-11 湖南省教育廳資助項目(08C121);湖南科技學院一般項目(09XKYTC008)。 郭美珍(1977-),女,湖南永州人,碩士,講師,研究方向: 微分方程數值解。 (責任編校:劉志壯)
2. 模型的主要結果





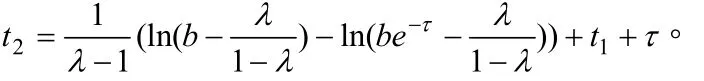







3 結 論

