求解集中載荷下復雜邊界條件厚板的撓曲方程

張 丹

（湖南科技學院 數學與計算科學系，湖南 永州 425100）

求解集中載荷下復雜邊界條件厚板的撓曲方程

張 丹

（湖南科技學院 數學與計算科學系，湖南 永州 425100）

應用功的互等定理， 得到了兩鄰邊簡支另兩鄰邊自由且角點支承的厚矩形板在集中載荷作用下的撓曲面方程；同時, 通過編程計算給出了具有實際價值的數值結果，進一步證明了應用功的互等法求解厚矩形板的正確性和優越性。

功的互等定理法；基本解；撓曲方程；Reissner理論；集中載荷

0 引 言

功的互等法(RTM)是付寶連教授提出的求解板殼力學及彈性力學平衡、穩定和振動問題的一個系統的方法[1-3]。功的互等法求解厚板問題的基本思想是將功的互等定理應用在實際系統和基本系統之間，從而得到實際系統的位移方程，并根據邊界條件得到該位移方程得最終解。對于求解厚板彎曲的方法，有疊加法，變分法和有限元法等方法，其中疊加法的應用最廣泛，與疊加法比，功的互等法具有求解簡單、準確等優點。

本文將功的互等法推廣于求解基于Reissner理論的厚矩形板彎曲問題，利用功的互等法研究集中載荷下兩鄰邊簡支另兩鄰邊自由且角點支承的厚板的彎曲情況。

1 基本方程

對于Reissner理論[4-5]，控制方程為

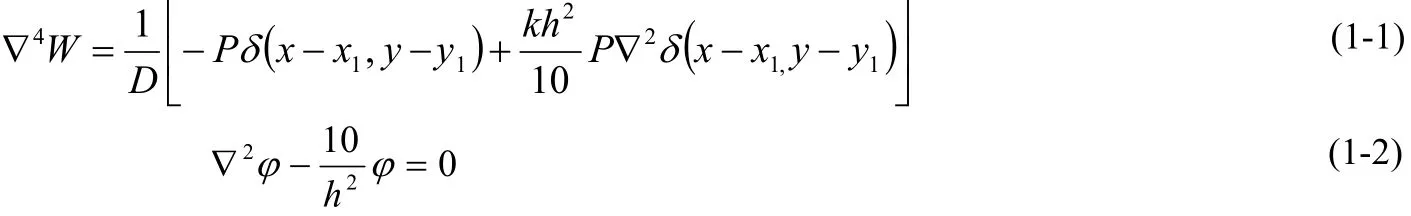
切力，彎矩，扭矩和轉角如下：

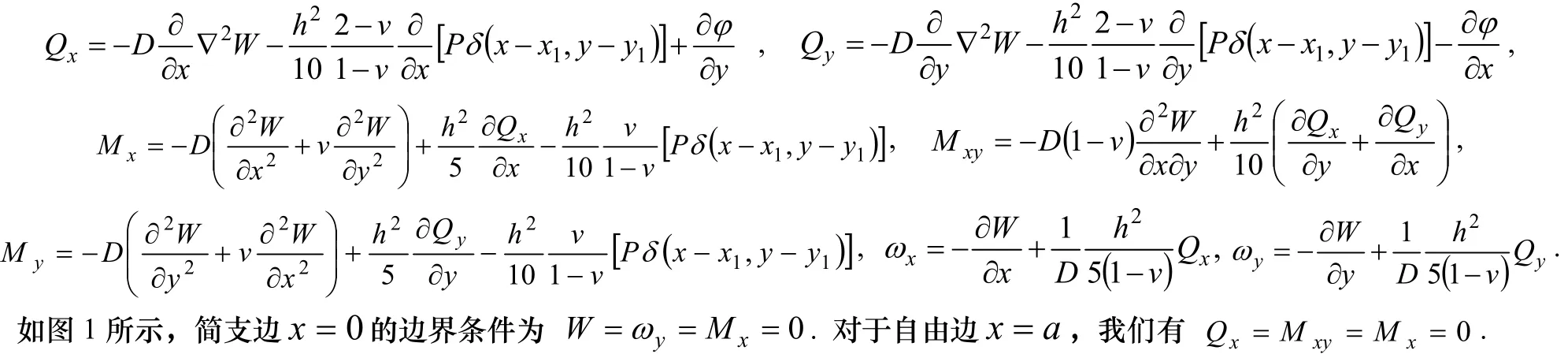
2 基本解

如圖2所示，取只受單位橫向二維Dirack-delta函數 (x ? , y ?)作用的簡支矩形板為基本系統，在這種情況下，控制方程(1-1)成為

我們稱該基本系統的解為基本解。易知該基本解為

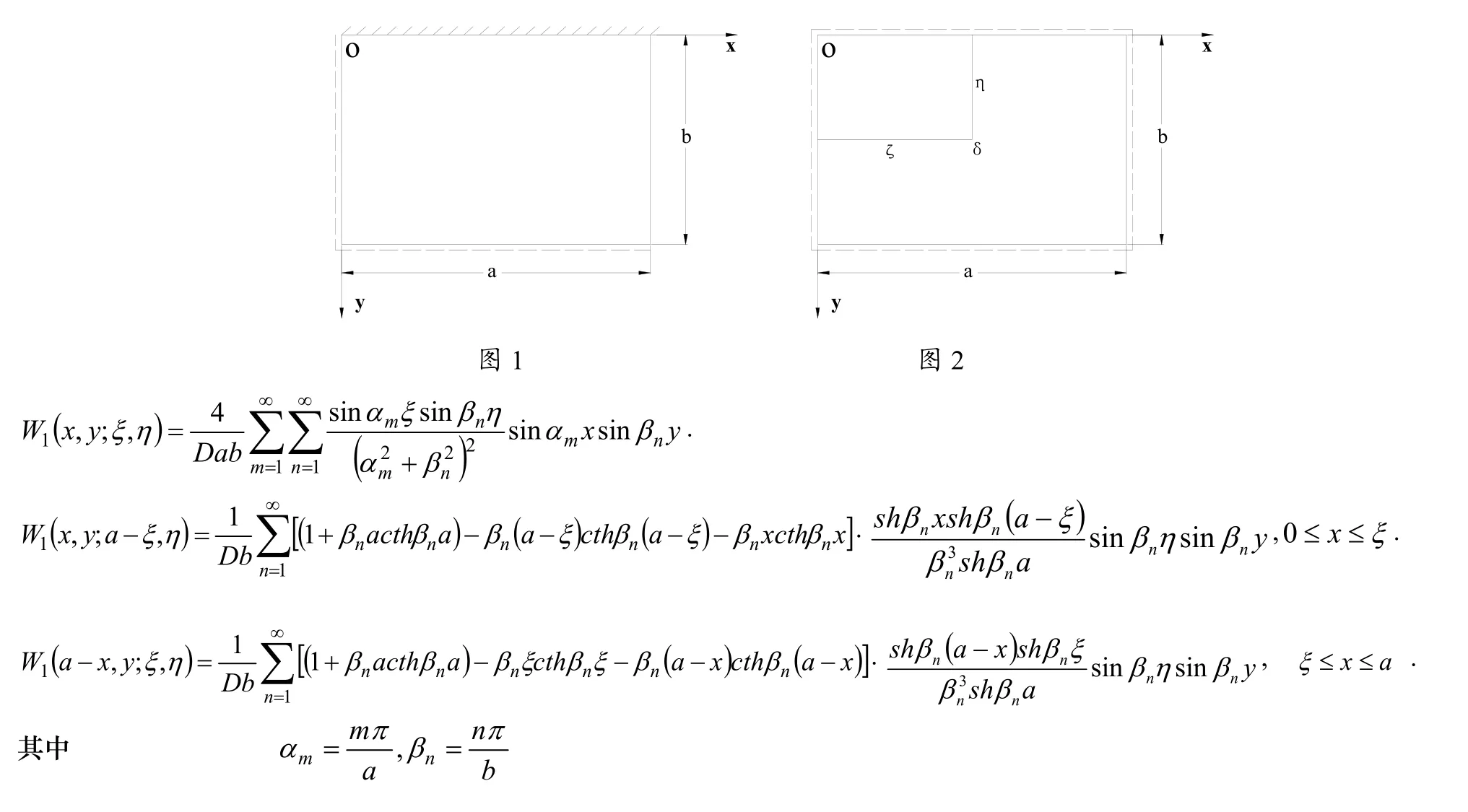
3 兩鄰邊簡支另兩鄰邊自由且角點支承的厚矩形板

我們將應用功的互等定理法求解如圖3所示在集中載荷 P作用下兩鄰邊簡支另兩鄰邊自由且角點支承的厚矩形板的彎曲。

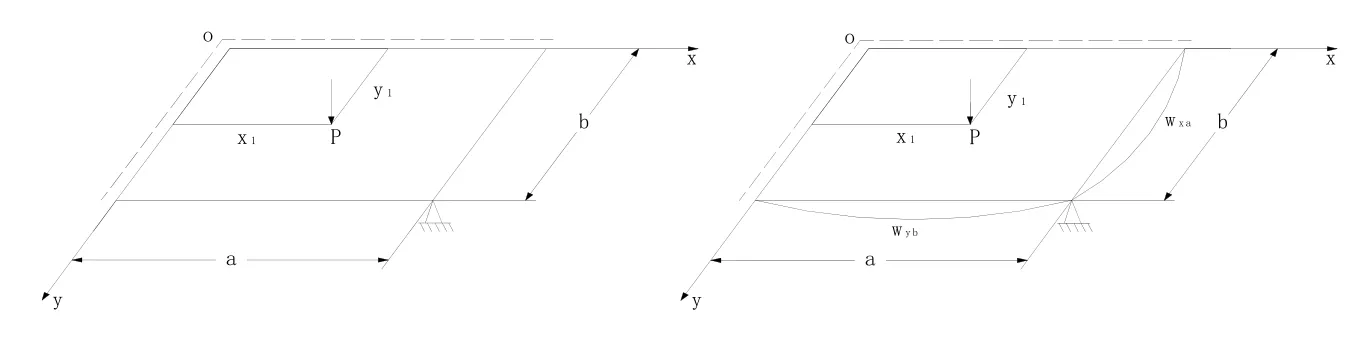
圖3 兩鄰邊簡支另兩鄰邊自由且角點支承的厚矩形板

如圖3所示，以在板面上作用有集中載荷P，兩鄰邊簡支另兩鄰邊自由且角點支承的厚矩形板作為實際系統。設

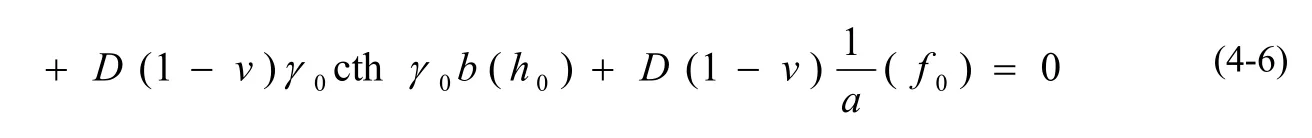
5 算法設計

本例中含有六組未知參數,,,,mnmnhfdb00,hf，其中Λ,3,2,1,=nm，系數矩陣也按對應順序擺布，先生成分塊子矩陣，再組合生成整體系數矩陣，在Matlab中采用選主元LU分解法解邊界方程組，取 80, =nm ，結果見表1。

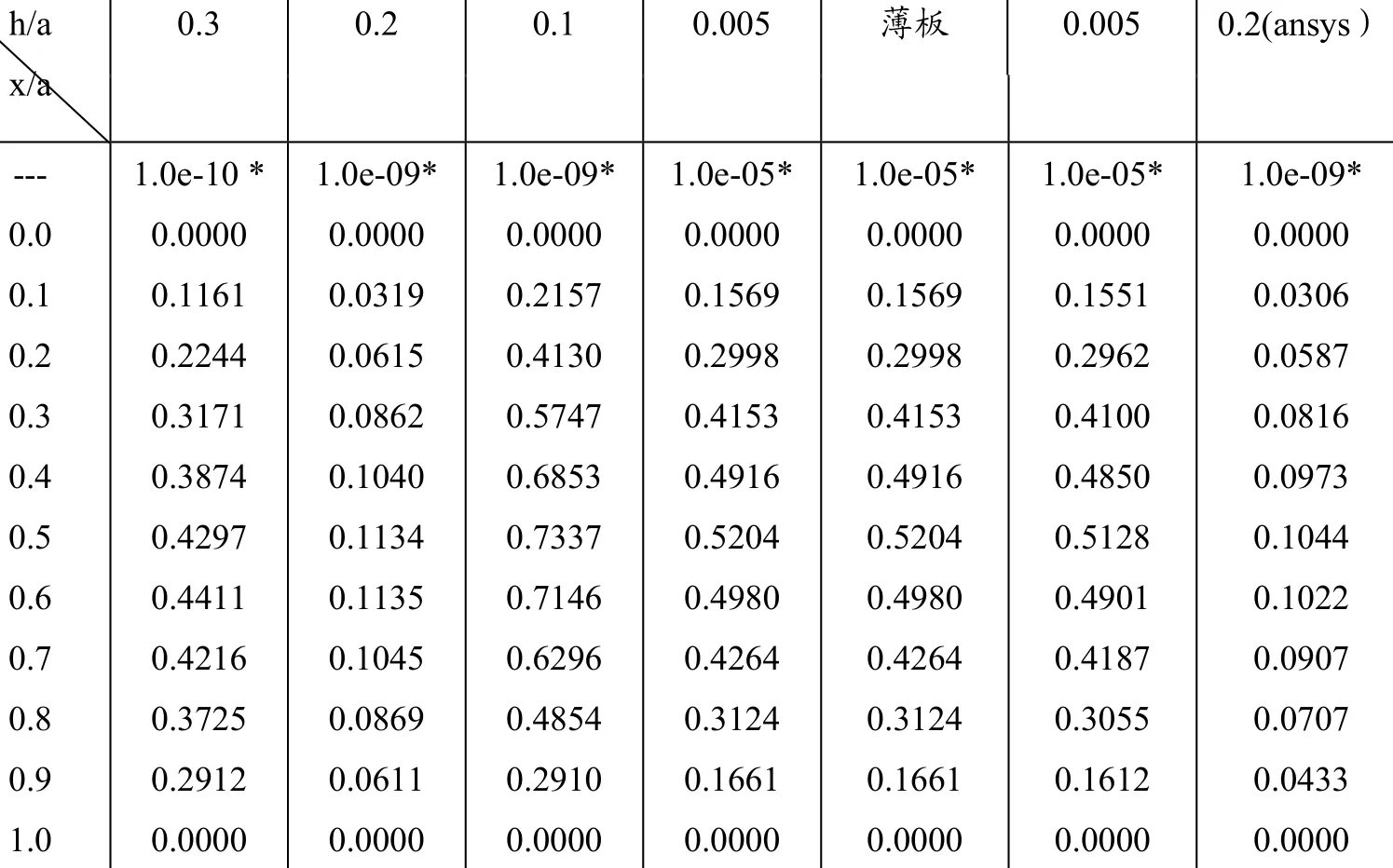
表1 by= 處 )(PW 沿 變化數據表

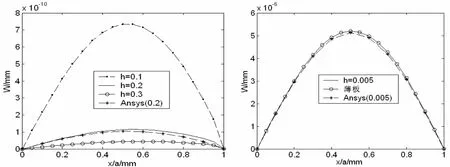
圖4 y b= 處 )(PW 沿 變化曲線

6 數值分析

表1、圖4分別給出了在 y = b 2處，撓度沿 變化的數據表和分布曲線，因厚跨比的變化而得到不同的結果。計算中參數分別取 a b =1,E = 3e11P a,v = 0.3,h / a=0.005,0.1,0.2,0.3.以 h / a =0.2為例，與ansys的計算結果比較，兩者能夠很好擬合；且當厚板中h很小時與薄板撓度的計算結果完全一致。這充分說明了利用功的互等定理求解厚板彎曲問題的正確性及算法選擇與程序設計的正確性。

[1]付寶連.彎曲薄板功的互等新理論[M].北京:科學出版社, 2003.

[2]付寶連. 關于求解彈性力學平面問題的功的互等定理法[J]. 應用數學和力學, 1989. 10(5):437-466.

[3]付寶連, 陳英杰. 應用功的互等定理求解中厚板彎曲[J]. 東北重型機械學院學報, 1995.1.13(1):83-90.

[4]苗天德, 程昌鈞. 關于彈性板彎曲變形的Reissner理論.

[5]E. Reissner. On the Theory of Bending of Elastic Plates[J]. J. Math. Phys, 1944, 23:184.

A

1673-2219（2011）12-0005-04

2011－10－12

湖南科技學院2009年重點科研課題資助。

張丹（1982－），女，在讀博士，數學系講師，研究方向為有限元數值方法和脈沖微分動力系統。

（責任編校：何俊華）