幾乎強次亞緊空間的無限乘積性質

紀廣月

(肇慶工商學院工商系，廣東 肇慶 526020)

幾乎強次亞緊空間的無限乘積性質

紀廣月

(肇慶工商學院工商系，廣東 肇慶 526020)

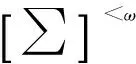
幾乎強次亞緊；|λ|-仿緊；可數仿緊

1999年E.Grabner 等在文獻[1]首先引入了幾乎亞緊空間的概念，并對其進行了初步研究，以后曹金文教授在文獻[2]分別對幾乎仿緊、幾乎次亞緊空間進行過研究。下面，筆者對幾乎強次亞緊空間進行了研究，獲得了無限個因子的乘積的2個等價定理。

1 基本概念

定義1 集族C稱為是定向的，如果?S,S′∈C，存在T∈C，使得S∪S′?T。設(Σ，≤)是一個定向集，集族U={Uα,α∈Σ}是定向上升的，如果對?α,β∈Σ時，當α≤β時，有Uα?Uβ。

定義2 設k是一個基數且λ≥2，空間x稱為是λ-仿緊的，如果x的每個勢≤λ的開覆蓋有一個局部有限的開加細。

定義3 空間x稱為幾乎強次亞緊空間，若對x的每個開覆蓋U，存在x的一個稠密子集D和U的開加細序列〈Vn〉n∈ω，使得對于?x∈D，存在nx∈ω，使得?n≥nx，有ord(x,Vn)<ω。

引理1[5]設λ是一個基數，如果空間x是λ-仿緊的，Σ是一個定向集且|Σ|=λ,{Hσ:σ∈Σ}是x的一個定向上升開覆蓋，則存在X的定向上升開覆蓋{Kσ:σ∈Σ}使得?σ∈Σ,有clKσ?Hσ。

根據定義3，有下面的引理：

引理2 幾乎強次亞緊空間的閉子集是幾乎強次亞緊的。

2 主要結論

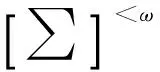
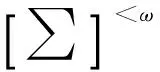
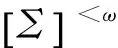
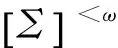
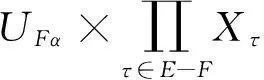
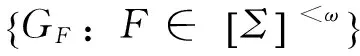
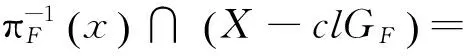
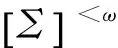
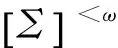
(yτ)τ∈H?TH=YH-πH(X-clGH)

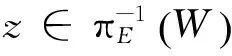
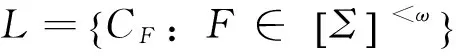
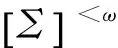
則〈Hn〉n∈ω是U={Uα,α∈Σ}的開加細序列。

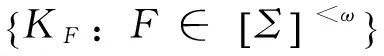
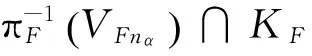
故[Hn]n∈ω是U={Uα,α∈Σ}的開加細序列。

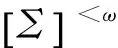
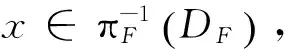
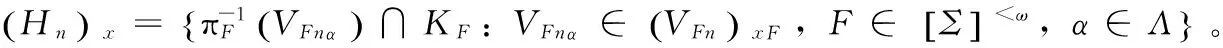
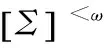
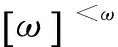
證明①?②是定理1的直接推論；②?③是顯然的，現在需證③?②。

[1]Grabner E, Grabner G.Nearly metacompact spaces [J].Topology Appl,1999,98:191-201.

[2]曹金文.幾乎次亞緊空間[J].黑龍江大學自然科學學報，2003,20(3)：50-53.

[3]Engelking R.General Topology[M].Warszawa:Polish Scientific Pusishers,1977.

[4]蔣繼光.一般拓撲學選講[M].成都：四川教育出版社，1991.

[5]Chiba K.Normality of inverse limits[J].Math Japonica,1990,35(5): 959-970.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.02.001

O189.11

A

1673-1409(2011)02-0001-02

2010-12-24

紀廣月(1973-)，女，1995年大學畢業，講師，碩士生，現主要從事一般拓撲學方面的研究工作;jiguangyue168@sina.com。