基于生產動態資料確定儲層滲透率非均質變化的參數反演數學模型

劉今子, 朱維耀, 張 偉, 龍運前, 岳 明

( 1. 北京科技大學 土木與環境工程學院,北京 100083; 2. 東北石油大學 數學科學與技術學院,黑龍江 大慶 163318; 3. 大慶油田測試技術服務分公司 第九大隊,黑龍江 大慶 163000 )

0 引言

在油藏實際勘探與開發過程中，經常遇到相鄰不遠處2口井的產量和產油能力有明顯差別.從油井取出的巖樣，甚至用肉眼觀察時，能發現其很多不同的性質.這種現象表明油藏具有不同的非均質性.油藏非均質性是油藏表征的核心內容，其研究水平將直接影響對油藏中油、氣、水的分布規律和開發效果，這是油氣勘探研究的熱點.針對油藏非均質性研究已取得長足進步，其研究內容和所涉及的領域不斷加深、擴大.研究油藏表征非均質特征的方法分為靜態方法和動態方法[1-4].

常用的靜態方法是巖心分析和地震測井，利用取得的數值進行空間插值，離散網格塊的參數值，進而描述油藏參數的空間非均質特征[1,5-6].反問題理論提供利用實測或動態數據結合先驗數據，反求地層參數分布，如孔隙度、滲透率等工具.對于研究非均質油藏表征滲流特征的反問題方面研究，主要有兩大方向：一是地震測井技術(靜態方法)，反演確定初始油藏參數分布；二是試井分析(動靜結合方法)，根據生產歷史資料，反演確定油藏參數分布的趨勢[7-9].用地震測井反問題方法表征油藏參數分布的局限性在于，用地球物理方法求滲透率大都必須依據巖心分析或其他資料，而且精度不高，只能代表井底周圍附近地帶的情況[10-12].用試井技術動靜結合歷史擬合的方法表征油藏參數分布的局限性在于，只能求得與井的產能直接相關的、代表井附近一定范圍的平均有效滲透率，并不能描述井網或區塊的油藏參數區域性非均質分布特點，也不能充分反映非均質油藏里流體的滲流特征[13-14].筆者針對儲層滲透率的不同非均質構型，建立二維單相反演優化分布數學模型，可以實現通過生產動態資料確定儲層滲透率的非均質構型參數.

1 構型表征

針對儲層滲透率的非均質特性，假定4種儲層滲透率K的分布：

(1)K是常數.

(2)K是線性變化：(a)線性遞增；(b)線性遞減.

(3)K是二次函數：(a)開口向上；(b)開口向下.

(4)K是對數函數或者指數函數：(a)對數函數(上凸)；(b)指數函數(下凸).

滲透率分布構型見圖1.

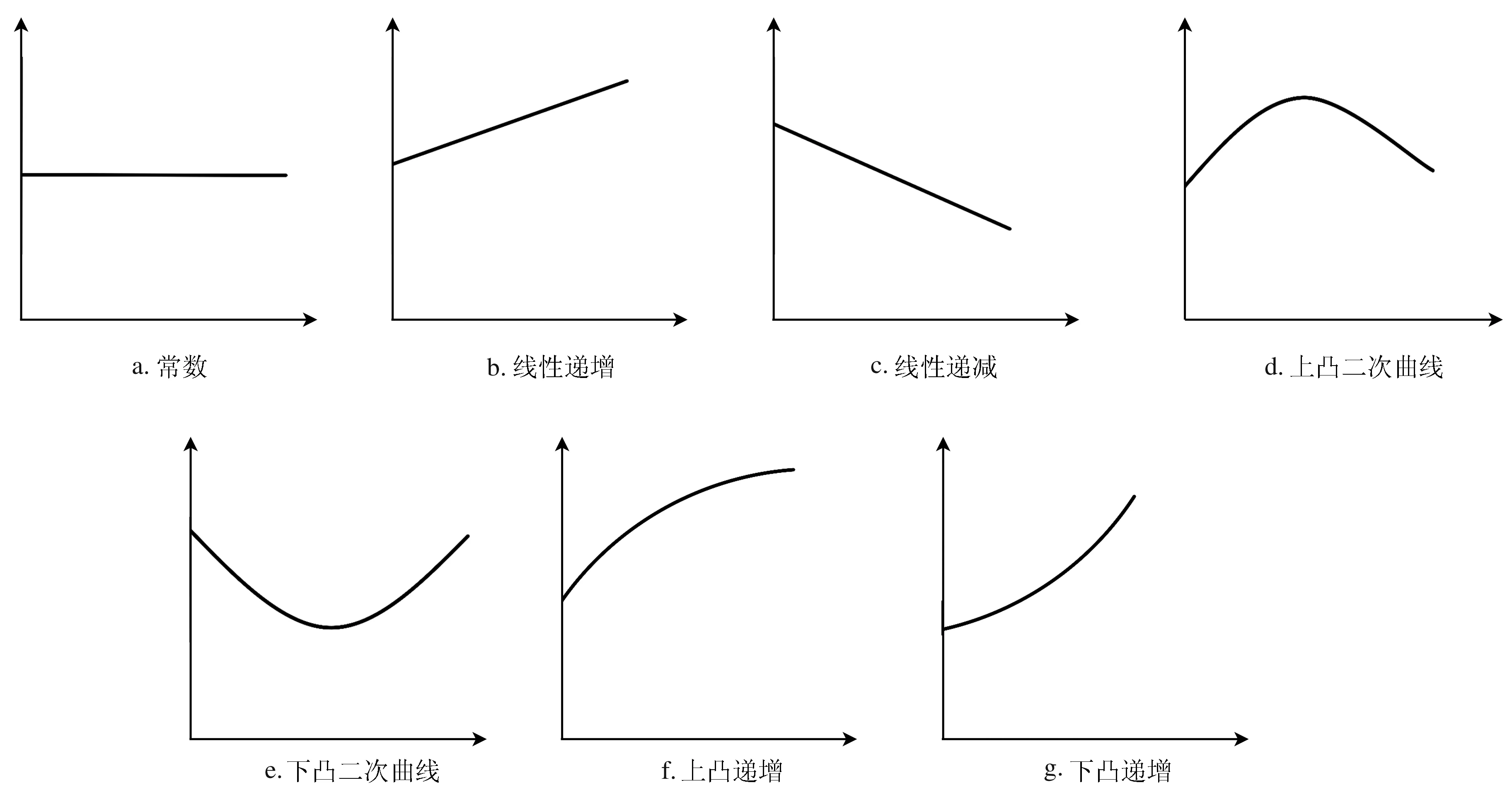
圖1 滲透率分布不同的構型示意

2 壓力梯度與流量的數學模型

針對平面徑向流的情況，物理模型：水平圓盤狀地層，均質等厚，r為地層任意點到井筒的距離，p為該點的壓力，h為厚度，供給邊界為圓形，pe為供給壓力，re為供給半徑.在圓的中心打1口水力完善井，rw為井的半徑，pw為井底壓力.同時，假設流體為牛頓流體，μ為黏度，與井軸垂直的每一個平面內的運動情況相同.在平面徑向流時，流線是1組流向點匯(生產井)或由點源(注水井)發散出來的直線，平面徑向滲流模型和平面徑向流壓力分布曲線分別見圖2和圖3.

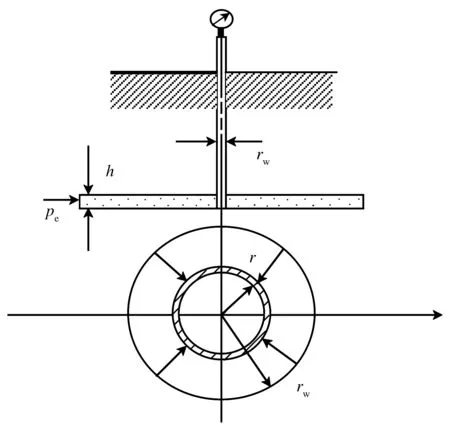
圖2 平面徑向滲流模型

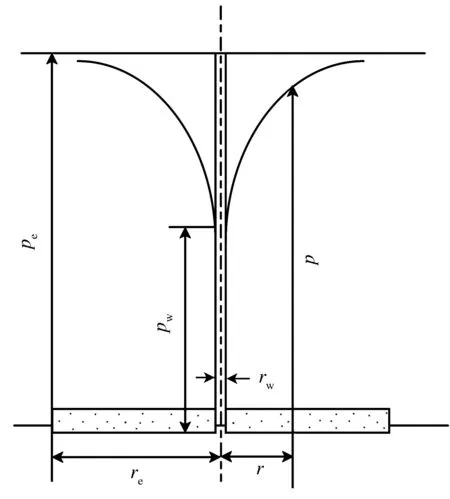
圖3 平面徑向流壓力分布曲線

2.1 儲層滲透率是常數

由已知條件，K(r)=K，代入達西定律，得

簡化得

(1)

2.2 儲層滲透率是線性變化

2.2.1 線性增加

由已知條件K(r)=a+br，a>0，b>0，代入達西定律，得

即

(2)

2.2.2 線性遞減

由已知條件K(r)=a-br，a>0，b>0，代入達西定律，得

即

(3)

2.3 儲層滲透率是二次函數變化

2.3.1 上凸

由已知條件K(r)=-ar2+br+c，a>0，b>0，c>0，代入達西定律，得

即

(4)

2.3.2 下凸

由已知條件K(r)=ar2-br+c，a>0，b>0，c>0代入達西定律，得

即

(5)

2.4 儲層滲透率是對數函數或者指數函數變化

2.4.1 對數函數上凸

由已知條件K(r)=alnr+b，a>0，b>0，代入達西定律，得

即

(6)

2.4.2 指數函數下凸

由已知條件K(r)=aebr，a>0，b>0，代入達西定律，得

即

(7)

3 反演模型

基于反演思路，建立針對儲層滲透率非均質特性的反演算法：

(2)輸入預估儲層滲透率的分布函數K(r)，得到預估壓力梯度p，流量q(取實際流量q*).

(3)如果預估儲層滲透率分布K(r)滿足實際的壓力梯度p*，應有

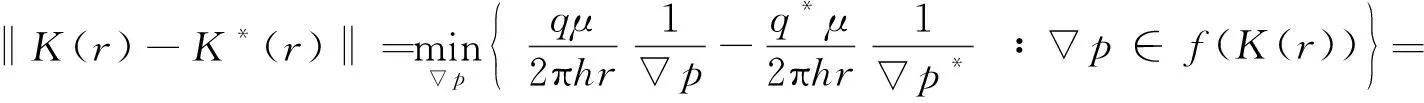
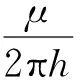
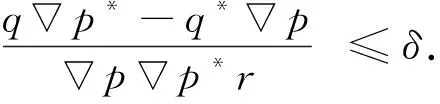
(8)

(4)如果滿足式(8)，預估值即可作為真實值；如果不滿足式(8)，由壓力梯度與儲層滲透率有判別函數關系為

校正預估儲層滲透率K(r)，校正函數關系為

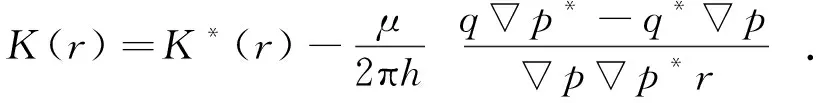
(5)將校正值作為預估值重新計算，得到壓力梯度，代入式(3)進行迭代.

(6)校正值K(r),滿足真實值K*(r)要求的精度.

4 數值模擬

以某低滲油田單井井史為例，進行儲層滲透率非均質性反演.油藏參數：井底的滲透率Ka=2×10-3μm2,邊界的滲透率Kb=8×10-3μm2，可以預估儲層滲透率非均質變化形態為3種形態：(1)線性遞增；(2)對數上凸；(3)指數下凸.當已知井底到邊界某一個點的壓力和產量時，可以進一步判斷是二次曲線上凸或下凸的形態.孔隙度為0.15；黏度為7.4 mPa·s；泄壓半徑為1 km；井筒半徑為0.1 m；儲層厚度為2 m.假定穩態情況時，井底流壓pw=7×106Pa，邊界壓力pe=17×106Pa，流量q=0.358 m3/d.利用文中建立的參數反演數學模型進行參數優化，其結果見表1.

表1 滲透率非均質性反演數值結果

由表1可見，儲層滲透率非均質變化形態為指數下凸時，迭代數值最穩定，其余的2種情況數值發散現象嚴重.據此可以判斷，此算例下的儲層滲透率非均質變化是呈指數下凸的構型.

5 結束語

根據儲層滲透率非均質構型的特點，建立不同儲層滲透率非均質構型下的滲流數學模型.考慮儲層滲透率非均質構型下，結合生產動態實際數據，建立反演儲層滲透率非均質變化的反演算法.算例表明，所建的結合生產動態資料反演儲層滲透率非均質變化的算法可以實現較高的精度，可以作為建立三維兩相反演儲層滲透率非均質變化和分區相滲曲線的數學模型的理論基礎，以及一種輔助歷史擬合的方法.