基于雙歐拉模型的流化床氣固兩相流場數值模擬

朱 博， 王 強， 郭慧軍， 張瀟玲， 杜明俊

( 1. 遼寧石油化工大學 化學與材料科學學院，遼寧 撫順 113001； 2. 中國石油集團工程設計有限責任公司 華北分公司，河北 任丘 062552 )

0 引言

目前,對流化床床層內復雜動力學特性的研究，雖然取得一定的進展，但存在許多問題，如氣固相間曳力的選擇、顆粒相間作用機制、邊界條件處理、湍流模型選取等，研究大多依賴經驗技術和半經驗理論.隨著計算機科學及數值分析的不斷發展，逐漸形成氣固兩相流動數值模擬學科，預報流化床工作的全過程，并為工程流態化裝置的優化和放大設計提供一種新的手段.

人們對氣固流化床內兩相流場進行研究[1-8]，并取得一些有意義的成果.Alder B J等[4]首次在分子系統相間擴散數值模擬中提出硬球模型.Moon S J等[5]采用數值方法研究三維振動流化床中黏性顆粒的動力學行為,并發現瞬時振動產生的巨大張力有助于降低黏性顆粒形成的聚團.何成銓[6-7]等研究細粉催化劑在流化床中的密度分布規律，并得出分布圖和關系式.Gidaspow D[8]提出把顆粒作為連續相處理的雙流體模型，并且成功預測鼓泡床流體力學行為.楊太陽等[9]在雙流體模型基礎上發展針對氣泡的模擬程序，成功模擬鼓泡床中氣泡頻率、速度、長度特征及顆粒循環狀態.

圖1 流化床物理模型(單位:m)

對于氣固兩相流動，相間曳力是表征兩相之間相互作用和動量交換的重要參數，決定數值計算總體的準確性[10].對于低流化風速下，采用Syamlal-O’Brien曳力模型計算床內流化過程誤差較大[11-12].結合實驗數據，筆者對Syamlal-O’Brien曳力模型進行修正，利用FLUENT軟件自帶的雙歐拉模型對均勻床內低速氣固兩相流場進行數值計算，為進一步改善和推動氣固兩相流動數值模擬的發展提供依據.

1 模型修正

實驗和數值模擬采用高1.00 m，直徑為0.15 m帶分布板的鼓泡床，入口空氣流速為0.25 m/s.頂部壓力為標準大氣壓，固相區充滿粒狀固體，體積分數為55%，簡化的流化床物理模型見圖1.利用Gambit進行建模和網格劃分.采用結構化矩形網格進行單元劃分，并通過床層壓降確定模型最適宜的網格數(30 480個).

1.1 數學模型

應用較廣泛的氣固兩相流模型包括歐拉-歐拉擬流體和歐拉-拉格朗日離散相模型，基于計算機資源的限制，大多采用歐拉-歐拉擬流體模型進行數值計算[13-14].在實際流態化過程中，薩夫曼升力對于大粒徑顆粒影響較大，對于粒徑遠小于粒子間距的鼓泡床，可忽略升力對主相流場的影響[14].對于虛擬質量力，當第二相密度遠小于主相密度時，虛擬質量影響較大，不能忽略，鼓泡床中第二相顆粒的密度遠大于主相氣體的密度，因此該項可以忽略[14].采用雙歐拉模型對低流化風速下氣固兩相流場進行數值計算，可以忽略升力、虛擬質量力及壁面滑移邊界對流態化過程的影響.

質量守恒方程為

(1)

動量守恒方程為

(2)

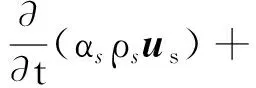
(3)

式中：αv，αs分別為氣相和固相的體積分數；uv,us分別為氣相和固相的速度矢量；ρv，ρs分別為氣相和固相的密度；p為兩相共享壓力；τ為壓力應變張量；Rvs，Rsv分別為氣相和固相間曳力；分別為氣相和固相間質量傳遞；usv，uvs分別為氣相和固相間速度；g為重力加速度.

1.2 修正Syamlal-O’Brien阻力模型

最小流化速度是指流化床層開始流化時的氣體空床線速.原Syamlal-O’Brien阻力模型計算的最小流化速度為0.21 m/s，不能滿足低速流化床相間阻力的計算，結合實驗數據，重新對相對雷諾數和曳力系數進行界定，對原有的Syamlal-O’Brien阻力模型進行修正，使其滿足低速流化過程.

曳力f計算模型為

(4)

式中：CD為曳力函數；Res為相對雷諾數；vr,s為固相沉降速率.

曳力函數CD采用Dalla Valle給出的形式：

(5)

這個模型是基于流化床或沉淀床顆粒的末端速度的測量，并使用體積分數和相對雷諾數的函數關系式：

(6)

式中：ρl為液相黏度；ds為固相顆粒直徑；vs為固相速度；vl為液相速度；μl為液相黏度.

液—固交換系數Ksl為

(7)

式中：αs,αl分別為固相和液相分數.

固相自由沉降速度系數為

(8)

1.3 邊界條件

計算時，固相顆粒密度為2 600 kg/m3,剪切黏度為1.789×10-5Pa·s,粒徑為0.2 mm,氣相密度為1.2 kg/m3，剪切黏度為1.89×10-5Pa·s.

入口邊界條件為

出口邊界條件為

2 數值模擬

實驗裝置由流化床和輔助設備組成，靜床高度為1.00 m,直徑為0.15 m,固體顆粒采用Geldart B類顆粒，空氣為流化氣體，實驗在常溫常壓下進行，實驗裝置及流程見圖2.通過實驗測得最小流化速度為0.80 m/s.

數值計算采用FLUENT 6.3軟件，并對其進行二次開發，利用C語言編寫UDF程序實現修正后Syamlal-O’Brien模型的計算過程，采用一階迎風格式對控制方程進行離散，利用Phass Coupled SIMPLE算法進行求解，迭代步長為1 ms,修正壓力和速度的松弛因子，使其快速收斂.

穩定進氣10 s后流化床軸向壓力變化的實驗結果與計算結果見圖3.由圖3可知，采用修正Syamlal-O’Brien曳力模型計算結果小于實驗結果，但軸向壓降變化趨勢相同，這主要是受固體顆粒球形度的影響.對比計算結果和實驗結果，最大相對誤差為4.4%，滿足工程實際要求，修正模型能夠描述低速氣固兩相流動相互作用物理過程.

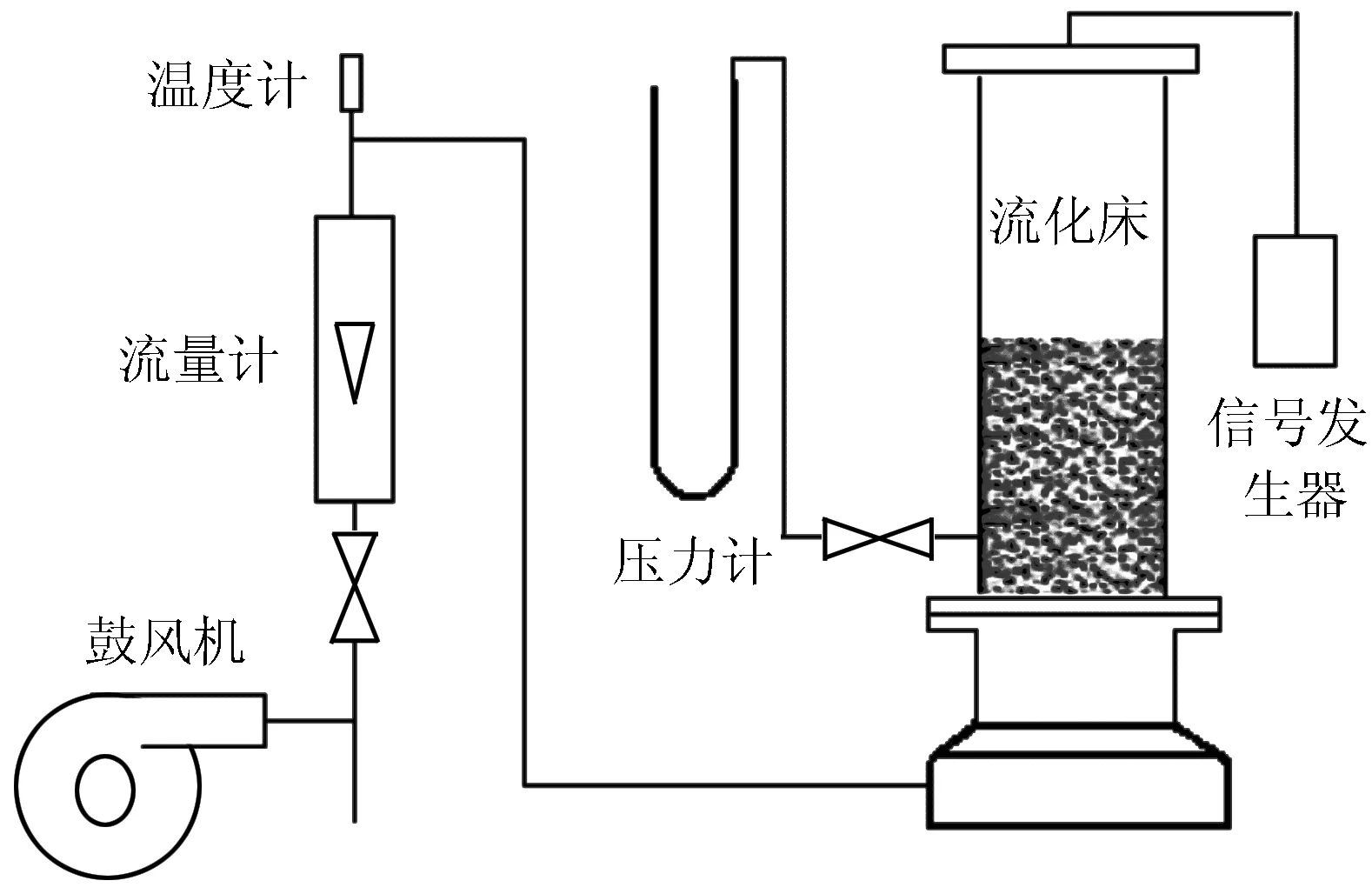
圖2 流化床實驗裝置及流程

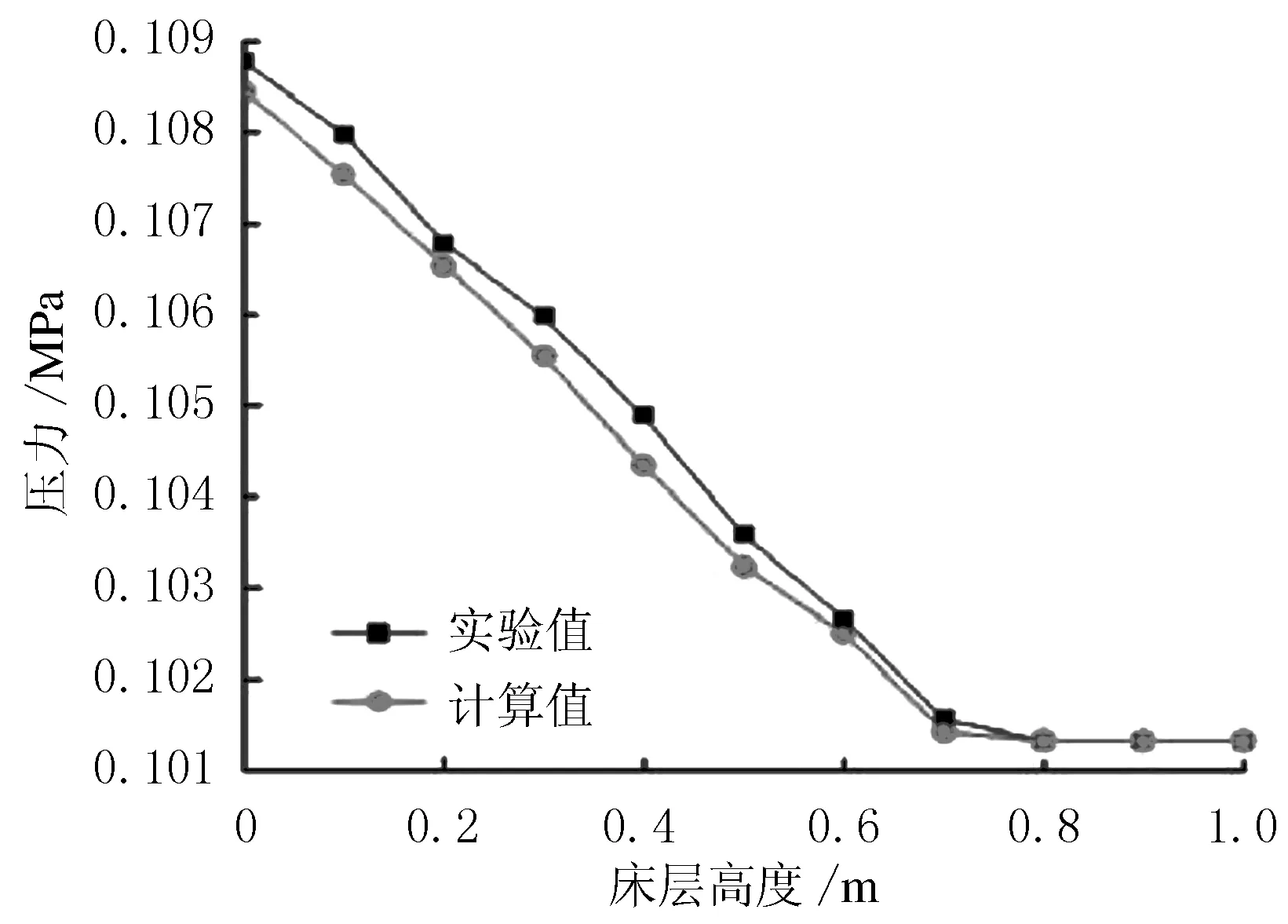
圖3 10 s后流化床軸向壓力變化曲線

Syamlal-O’Brien阻力模型修正前后不同時刻流化床固相顆粒體積濃度云圖見圖4.由圖4可知，修正前模型在0.8 s后開始出現氣泡，且隨著時間延長，氣泡不斷上升并長大；修正后模型在1.4 s后逐漸產生氣泡，且氣泡增長和上升速度較慢.對于固相顆粒，修正前模型在1.5 s前均勻膨脹，之后在床底不均勻氣流的脈動下，開始出現不均勻膨脹，且密相床層高度隨之降低；修正后模型在2.0 s前上部顆粒均勻膨脹.流態化初期，密相床層軸向上存在速度差，導致高度方向上流態化氣速大小不一，較低的氣速使流化床床層發生均勻膨脹，較高的氣速導致氣泡生成.由于計算所用顆粒直徑為0.2 mm，屬于流態化原理中Geldart B類顆粒，該類顆粒在流態化氣速較小時流化床床層先發生均勻膨脹而無氣泡生成，隨著流態化氣速增大至鼓泡速度時才出現氣泡.修正后模型計算結果與流態化原理[15]導出的結論一致.

穩定進氣2.0 s后不同介質流化床軸向壓力變化曲線見圖5.由圖5可知，靠近床層底部一定區域，修正后的曳力模型計算的固相和氣相床層壓力大于原模型的，且隨床層高度的增加壓力逐漸降低，主要是修正曳力模型計算的氣泡聚并與破裂頻率降低引起的.流化床床內壓力場的分布受氣泡狀態及進氣氣流影響，采用原曳力模型計算的固相介質和氣相介質的軸向壓力波動較大，主要原因是修正前模型計算的最小流化速度偏大，短時間內出現大量氣泡，隨著氣泡的不斷上升、融合和破碎，使固相區出現不均勻膨脹，從而導致床層壓力開始大幅度不規則波動，此時床層壓降受脈動氣流頻率和氣泡行為共同控制.修正后模型計算壓力波動的范圍較小，主要原因是初始流化速度小，床層壓力主要受脈動氣流波動控制，使床內固相顆粒均勻膨脹.

圖4 不同時刻流化床固相顆粒體積濃度云圖

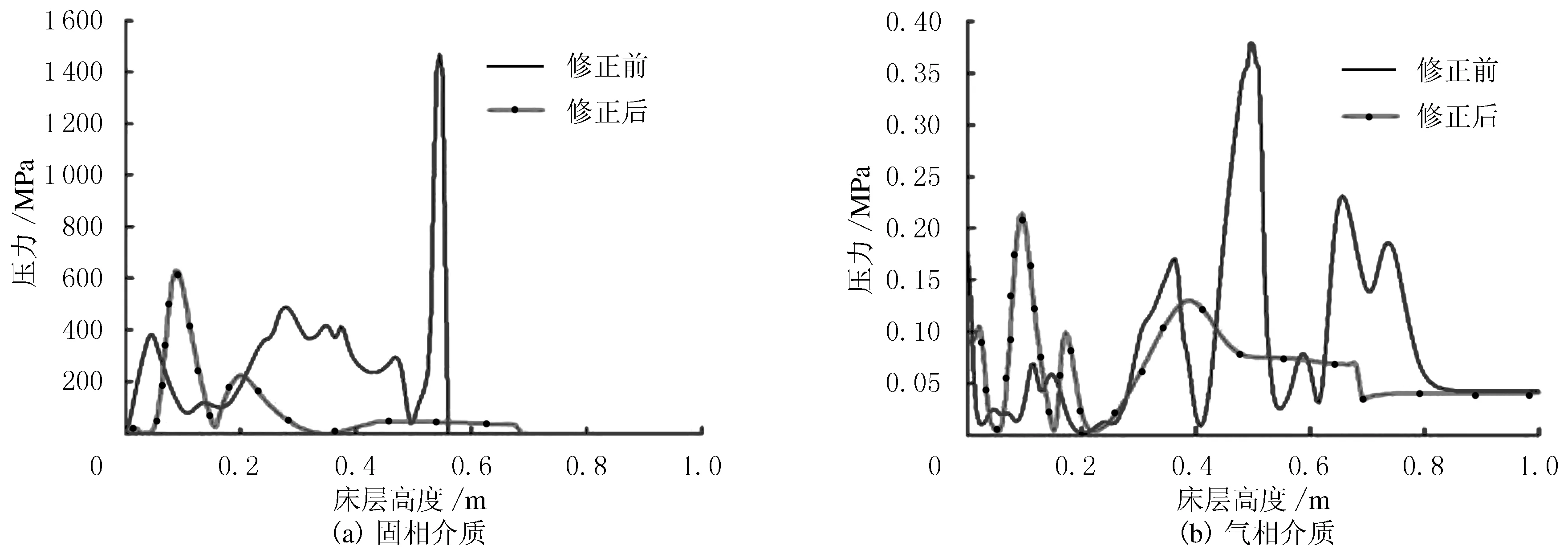
圖5 2.0 s后不同介質流化床軸向壓力變化曲線

3 結論

(1)結合實驗數據，對體積分數和相對雷諾數進行重新界定，修正Syamlal-O’Brien曳力模型，使其最小流化速度為0.80 m/s,滿足低流化風速條件.

(2)結合修正后曳力模型，采用雙歐拉模型對均勻床內低速氣固兩相流場進行數值計算，計算結果比實驗數據略小，最大相對誤差為4.4%，滿足工程實際要求.

(3)由于Syamlal-O’Brien阻力模型是根據床層壓降、表觀氣速、床層膨脹比等實驗數據得到的半經驗公式，是在單個顆粒曳力模型的基礎上引入顆粒體積分數描述對周圍顆粒的影響，建議結合實驗，根據數學理論和數值模擬等繼續完善一個相對完整的阻力模型.