Newton-Leipnik系統混沌控制

李賢麗， 秦顯榮， 王 升， 張秀龍， 嚴曉波

( 東北石油大學 電子科學學院，黑龍江 大慶 163318 )

0 引言

自1963年Lorenz在確定性系統中發現混沌運動以來，混沌及相關問題研究取得許多進展.由于混沌現象普遍存在于復雜的非線性系統中，混沌控制是混沌應用的關鍵技術，已經成為非線性科學的重要研究領域.自1990年Ott E等提出OGY方法[1]實現混沌控制以來，許多控制方法，如周期激勵法[2]、參數周期擾動法[3]、自適應控制法[4]、線性反饋法等均可實現混沌控制，并在許多領域中得到應用.

混沌控制方法可以分為反饋控制和無反饋控制[5].反饋控制方法可以根據受控系統的狀態進行調節，具有微擾較小的優點，但需要預先了解系統的運動狀態.實際的非線性系統常常無法預先了解系統的動力學特性.無反饋控制方法不必預先了解系統的狀態變量，在實際控制中簡單易行，因而在許多領域得到應用.無反饋控制方法多應用于非自治系統的混沌控制，對于自治系統的控制研究較少.李賢麗等[6-8]采用參數周期擾動、周期激勵、周期脈沖等無反饋控制方法，對自治系統，如CHAY模型、Rossler系統、Lorenz超混沌系統等進行研究，得到較好的控制結果.

Leipnik R B等在研究具有線性反饋的剛體運動模型時，提出具有雙吸引子的Newton-Leipnik混沌系統[9]，該系統在初始條件不同時，存在2個不同的吸引子，因而系統動力學性質更為復雜[10-12].筆者采用周期激勵法和參數擾動控制法對Newton-Leipnik雙吸引子系統的混沌進行控制，以實現有效控制，并對不同初始條件混沌控制的影響進行比較.

1 Newton-Leipnik系統的動力學性質

1.1 動力學性質

具有雙吸引子的Newton-Leipnik混沌系統，為三維非線性自治系統，方程為

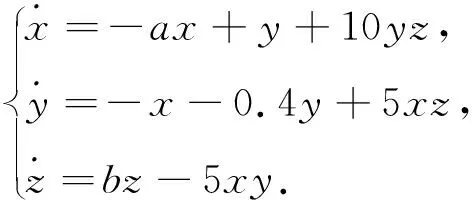
(1)

式中：a，b為參數.

當a=0.4，b=0.175時，系統的初始狀態取(0.349,0,-0.160)T和(0.349,0,-0.180)T時，系統的相軌跡見圖1.由圖1可以看出，系統存在著上、下2個不同的奇怪吸引子，因而Newton-Leipnik系統的動力學行為相對其他單奇怪吸引子系統更為復雜，對初始條件具有較強的敏感依賴性.

對式(1)求解，得到系統具有5個不穩定平衡態分別為(0,0,0)T，(0.239 0,0.030 8,0.210 3)T，(-0.239 0,-0.030 8,0.210 3)T，(0.031 5,-0.122 4,-0.110 3)T，(-0.031 5,0.122 4,-0.110 3)T，其中：第2、3個平衡態處于上吸引子的中心，第4、5個平衡態處于下吸引子的中心.根據線性穩定性分析，對第1個平衡態，在平衡點鄰域將方程線性化，得到3個特征值：

λ1=0.175 0,λ2=-0.4+i,λ3=-0.4-i.

對第2、3個平衡態，得到3個特征值：

λ1=-0.799 8,λ2=0.087 4+1.211 5i,λ3=0.087 4-1.211 5i.

對第4、5個平衡態，得到3個特征值：

λ1=-0.799 5,λ2=0.087 3+0.875 2i,λ3=0.087 3-0.875 2i.

因而這5個平衡態為不穩定焦結點.系統的初始條件決定系統相軌跡的運動趨勢，最后形成雙吸引子的復雜結構.當a變化時，在平衡態(0,0,0)T處，系統的線性化方程的特征值為

當a=-0.4時，系統從不穩定態經hopf分岔轉變為穩定的極限環型振蕩，即非線性周期運動.

1.2 數值計算

采用四階龍格—庫塔法，對非線性微分方程式(1)求數值解，得到xmax隨參數a變化分岔結構圖(見圖2)，其中：橫坐標為a，縱坐標為x的極大值，可以觀察到明顯的倍周期分岔通向混沌的過程，當a=0.36時，系統為2周期運動；當a=0.368時，系統為4周期運動.z隨t變化的時序圖見圖3和圖4.

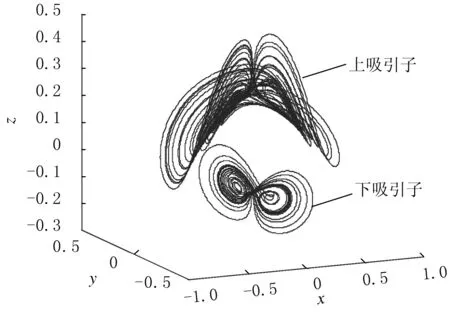
圖1 系統的奇怪吸引子

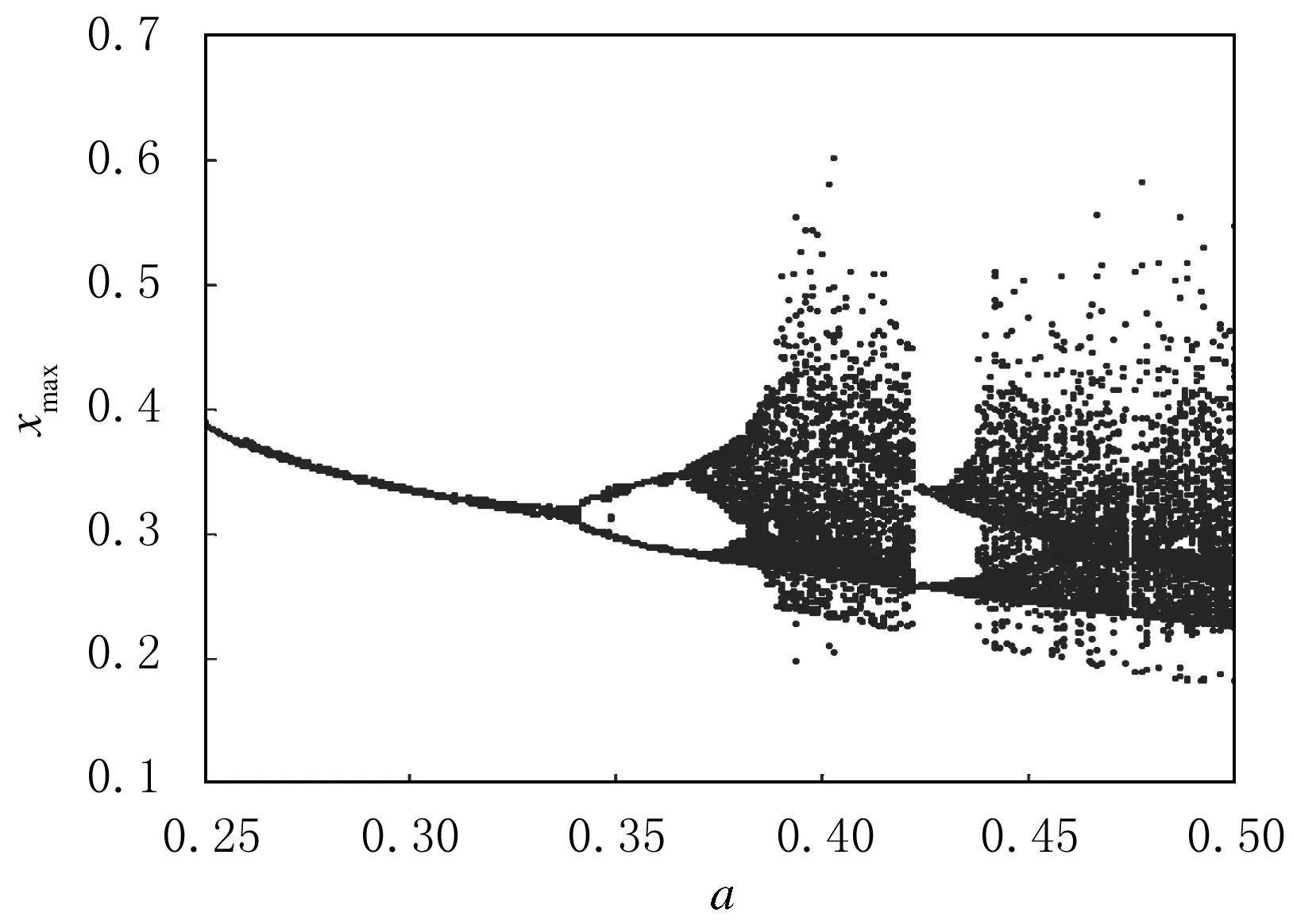
圖2 系統隨a變化的分岔圖

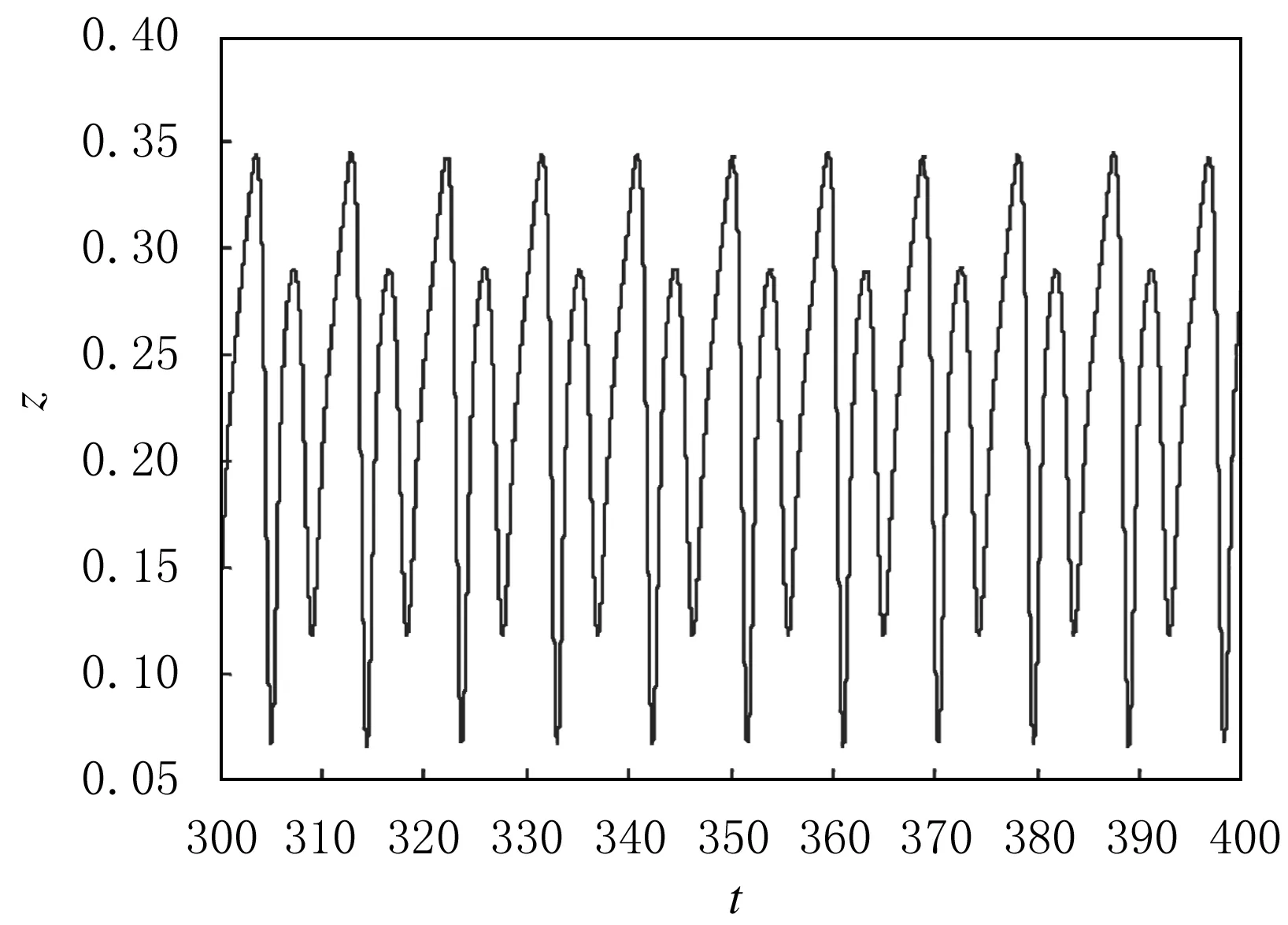
圖3 系統的2周期時序圖

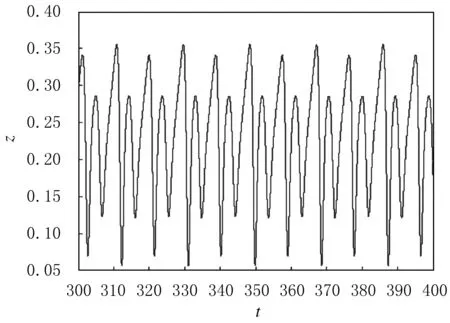
圖4 系統的4周期時序圖

2 混沌控制計算

在Newton-Leipnik系統中，取a=0.4，b=0.175時混沌運動狀態，選取初始條件為(0.349,0,-0.160)T作研究.采用周期激勵和參數周期擾動控制方法對Newton-Leipnik系統的混沌運動進行控制，它們根據混沌運動對初始條件的高度敏感性和混沌軌道中鑲嵌著無窮多個不穩定的周期軌道性質，利用共振原理和混沌軌道的遍歷性對系統的混沌運動進行抑制.

2.1 周期激勵控制

周期激勵法是通過給系統加入附加的周期強迫力的方法，控制動力學體系的混沌運動狀態.在方程(1)右側加入周期激勵項F：

F=rcosωt,

(2)

式中：r為周期激勵振幅；ω為激勵頻率.該方法可調參數為r和ω，通過適當調節它們實現混沌運動控制.

在系統方程(1)的第1式的右側加入周期性外力式(2)，方程為

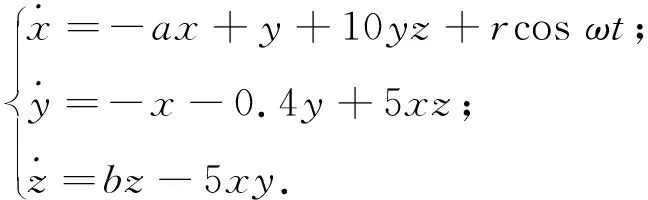
(3)

計算結果表明，當ω=3.2時，對控制參數r循環運算，得到控制結果隨激勵振幅r變化的結果見圖5(a)；當0.30≤r≤0.42時，能夠將混沌運動控制為規則周期運動，r=0.4時的系統三維相圖見圖5(b).

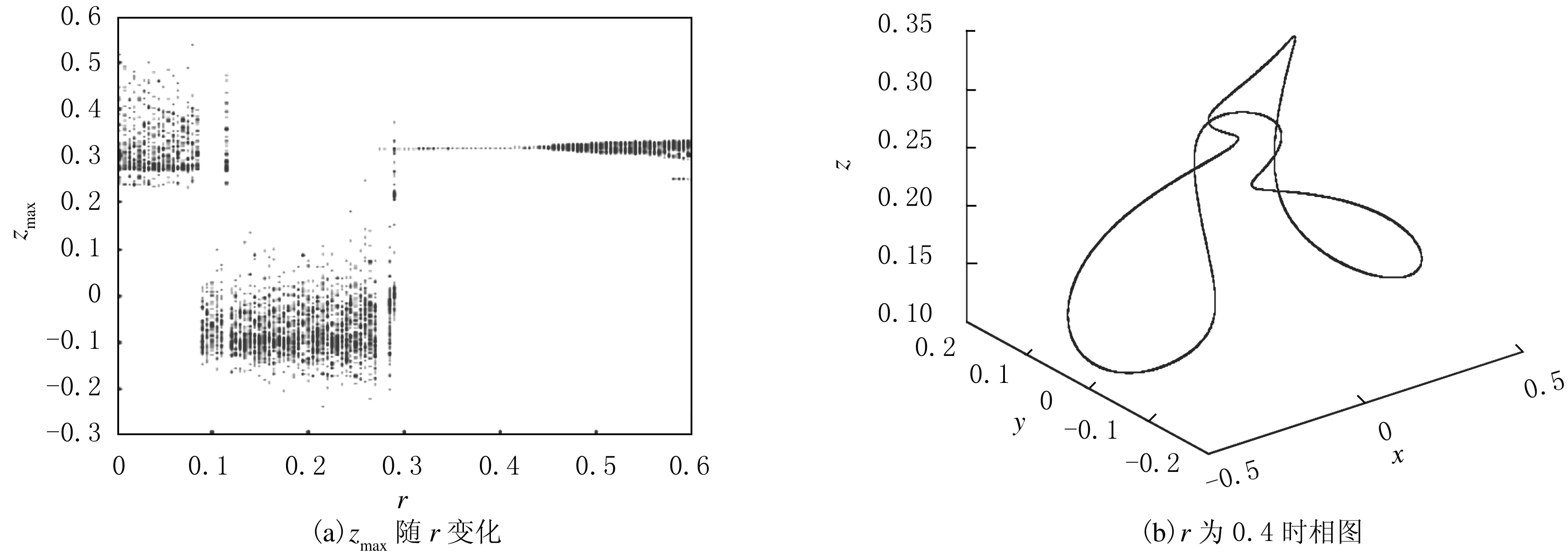
圖5 ω為3.2時的周期激勵控制

將式(2)加在系統方程(1)的第3式中，進行周期激勵控制.當ω=2.0時，得到控制結果隨激勵振幅r的變化(見圖6(a)).由圖6(a)可以看出：當0.14≤r≤0.3時，系統被控制為1周期運動.當r=0.2時，系統相圖見圖6(b).

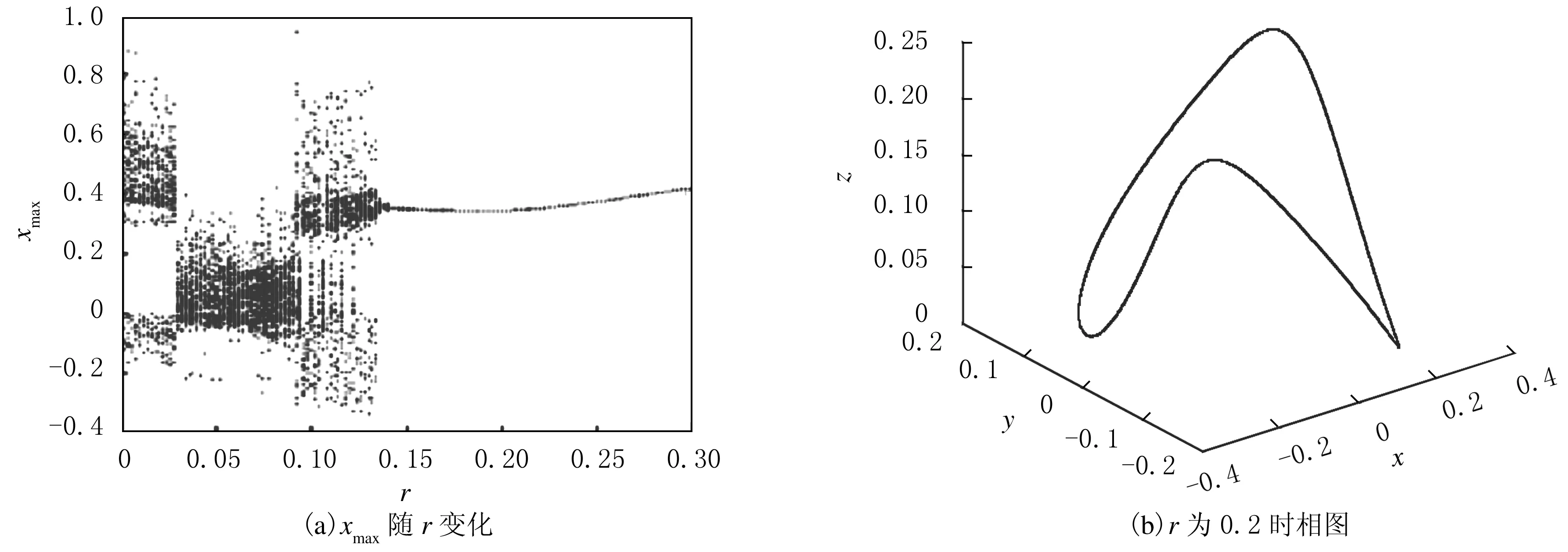
圖6 ω為2.0時的周期激勵控制

對系統方程第1和3式進行控制，均可實現控制.將控制后得到的周期態與原系統的周期態進行比較，控制得到穩定的周期軌道并不是原系統的周期軌道，系統的性質發生變化，產生新的動力學行為.

2.2 參數周期擾動控制

在系統方程中，選取a作為控制參數，對其進行周期擾動，即把式(1)的a改為

a′=(1+rcosωt)a,

(4)

式中：r為參數周期擾動的幅值；ω為參數周期擾動頻率.可以通過調節的控制參數r和ω，將系統的混沌態抑制為規則的周期運動，從而實現混沌控制.

將式(4)代入系統方程(1)中，則方程(1)的形式為

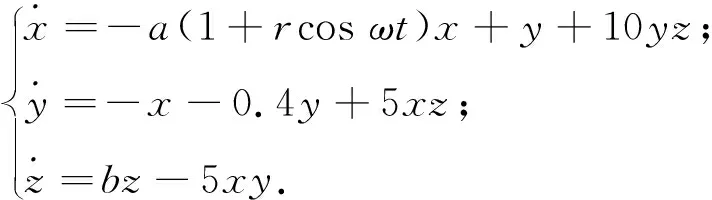
(5)

調節控制參數r和ω：當T=7.3時，改變控制幅值r得到穩定控制，當0.78≤r≤1.2時，除個別值外，系統能夠被穩定控制成1周期運動，系統受參數周期擾動后，得到控制結果隨r的變化(見圖7(a))；當r=0.8時，系統相圖見圖7(b).

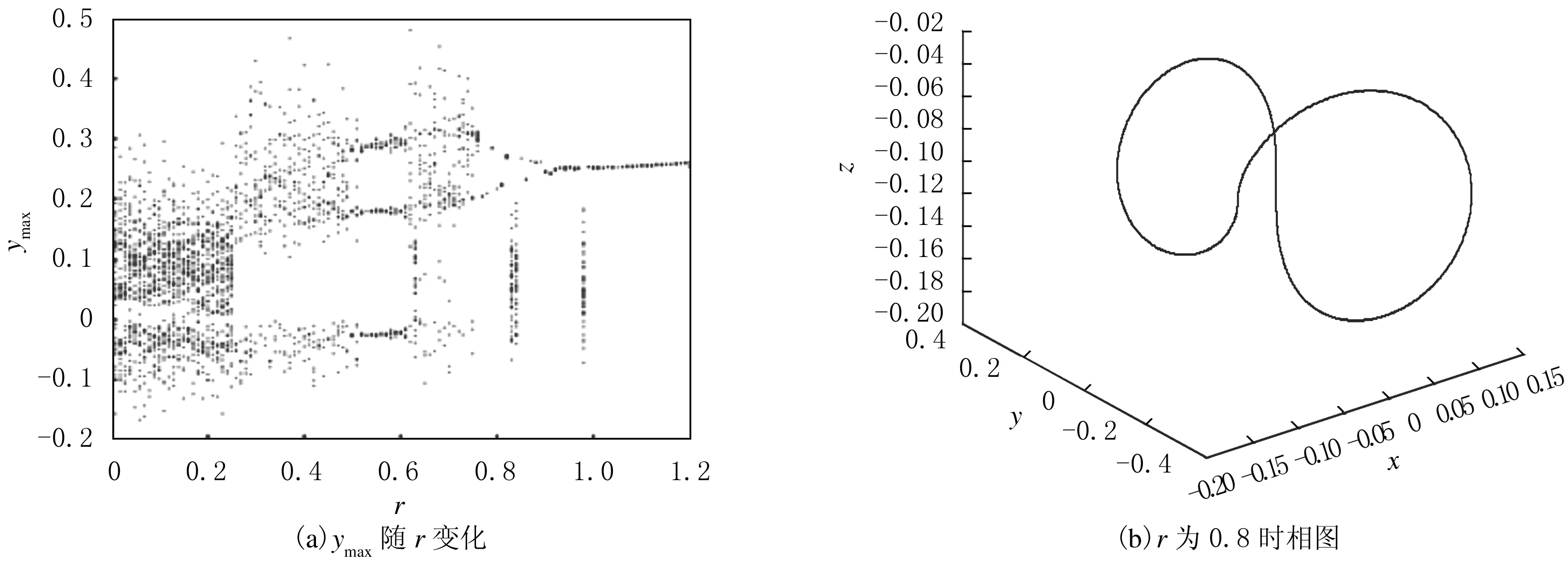
圖7 參數周期擾動控制

3 初始條件影響

由于雙吸引子結構特殊，受初始條件影響較大，不同初始條件對應上、下2個不同的吸引子，在控制過程中可能被吸引于不同的吸引域內，因而控制時達到的狀態有可能不同.當初始條件不同時，比較2種控制方法的控制結果.

對于周期激勵控制，當ω=5.0時，初始條件分別取 (0.349,0,-0.160)T和(0.349,0,-0.180)T時，控制結果與r變化關系見圖8.由圖8可以看出，2種方法存在一定差異.r=0.4時的控制相圖見圖9(a)，分別處于混沌和1周期運動狀態.r=0.55時的控制相圖見圖9(b)，分別處于1周期和混沌運動狀態.當r=0.6時均為1周期運動，且2條曲線完全重合，說明初始條件不同的2個吸引子最終控制的結果相同.

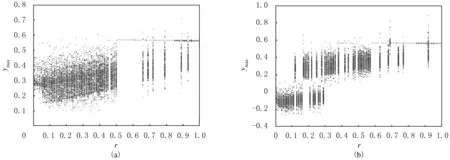
圖8 ω為5.0時周期激勵控制ymax隨r變化圖

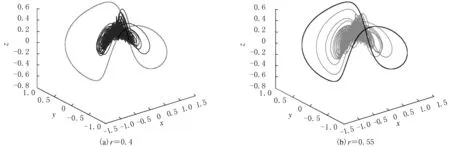
圖9 不同r時的相圖

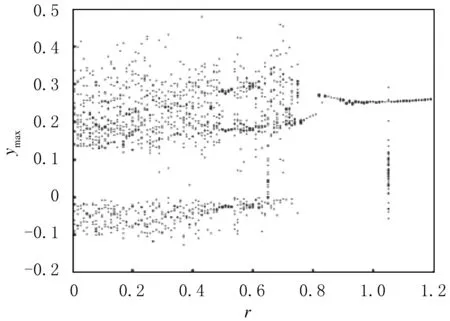
圖10 參數周期擾動控制

計算參數擾動控制，當T=7.3(ω=T/(2π))、初始條件取(0.349,0,-0.180)T時，控制結果見圖10.由圖10與圖8可以看出，在參數取某些特定值時，控制結果不同.對雙吸引子復雜系統，初始條件的微小變化對應系統的上、下2個吸引子，控制對系統性質有一定影響，致使控制結果出現差異，但對結果影響不大，可控區域重合范圍較大.

4 結論

(1)分析Newton-Leipnik雙吸引子系統的動力學性質，5個不穩定平衡態的存在導致該系統的性質較為復雜.采用周期激勵和參數周期擾動2種無反饋的控制法，研究該系統的混沌態控制，結果表明2種方法均可實現對該系統的混沌控制.

(2)2種方法的優點是無需預先了解體系的性質，即可對體系的混沌態進行控制，得到的穩定的周期軌道并不是原系統的周期軌道，系統的動力學性質發生變化.由于雙吸引子系統的復雜性質，具有對初始條件的高度敏感依賴性，對比不同初始條件下的2種混沌控制方法得到的結果，表明初始條件不同對控制結果有一定影響，但影響不大.

(3)實際復雜的混沌系統很難預先了解動力學特性，為解決這類問題的混沌控制提供依據，并且在混沌控制過程中能夠得到豐富的信息及新的動力學行為.