基于亞鐵磁材料－YIG的雙負電磁特異材料的設計及電磁特性研究＊

鄧躍龍，蔣練軍，賈平，熊翠秀，徐志峰

(1.益陽醫學高等專科學校公共課部，湖南益陽413000;2.湖南城市學院物理與電信工程系，湖南益陽413000)

基于亞鐵磁材料－YIG的雙負電磁特異材料的設計及電磁特性研究＊

鄧躍龍1，蔣練軍2，賈平1，熊翠秀2，徐志峰2

(1.益陽醫學高等專科學校公共課部，湖南益陽413000;2.湖南城市學院物理與電信工程系，湖南益陽413000)

基于磁導率為負的亞鐵磁材料－YIG，在其中嵌入等效介電常數為負的金屬導體線陣列結構，合成出雙負電磁特異材料。利用有效媒質理論數值，計算了復合材料的等效介電常數與等效磁導率的頻率響應特性。計算結果表明:在C波段電磁波頻率的重疊區域，使復合材料的等效介電常數與等效磁導率同時為負;表明了利用有效媒質理論基于亞鐵磁材料可以設計為負折射率特異材料。

有效媒質;亞鐵磁材料;金屬線陣;雙負材料

電磁特異材料是由一些人工制備的電磁共振單元組成，當探測電磁波的波長遠大于組成單元的晶格常數時，特異材料可以被看作是一種均勻的有效媒質，它具有等效介電常數和磁導率，這就是有效媒質的概念［1］。由于這種合成材料的特異功能和廣闊的應用前景，世界上很多研究小組都開始著手設計、制作、研究這種新型實用的雙負電磁特異材料。目前已有許多結構的雙負特異材料被設計制造出來，大致可分為三類，一類是以Smith的SRRs加TWs(Thinwires)結構為基礎的雙負材料［2－7］，另一類是以基于傳輸線理論設計的雙負介質型［8，9］，另外，還有學者對采用鐵氧體等鐵磁材料代替Smith結構中SRRs的功能來實現雙負電磁特異材料的方法進行了有益的探索，如Pimenov等采用超導金屬線加鐵磁材料的方法從理論上證明該方法可能合成新的雙負材料［10］，Yongxue He等也從理論上對此方法進行了有益的探索［11］。本文采用具有大飽和磁化強度的亞鐵磁材料基片中嵌入金屬導體線周期陣列設計寬帶雙負電磁特異材料，并擬在平面電磁波照射下研究其電磁傳輸特性。

一、絕緣型亞鐵磁材料－YIG磁導率的頻率響應特性分析

YIG對入射電磁波表現出各向異性，在Z方向外加恒定磁場H0時，其磁導率為一張量，可表示為:

角頻率為ω的線偏振平面波沿平行于磁化方向入射到YIG時，將分解為兩個旋轉方向相反的圓偏振本征波。兩組圓偏振本征波對應的相對磁導率μIr，p，μIIr，p以H0、M0、ΔH為參量，可得以電磁波頻率f為變量的解析解分別為:

基于YIG的實際物理參數，設置YIG在外加磁場H0=1200奧斯特作用下，其飽和磁化強度M0=1750高斯，相對介電常數εr=12.7，鐵磁共振線寬ΔH=40奧斯特。基于設置的物理參數，由公式(1.2)和(1.3)計算得到兩組本征波相對磁導率的頻率響應特性如圖1所示。

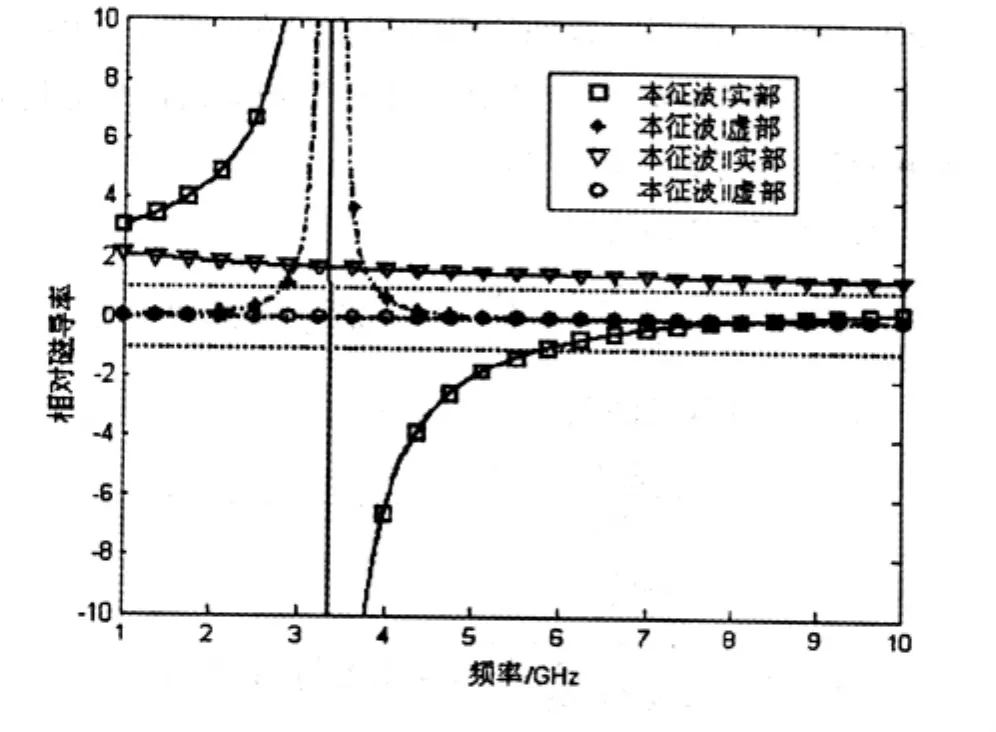
圖1 平行于磁化方向入射時，兩組本征波的相對磁導率的頻率響應特性

由圖1可知，在頻率3.36～8.26GHz范圍內，本征波I的相對磁導率的實部為負值，因此，本征波I在YIG中快速衰減而不能在其中傳播，因此，入射電磁波在YIG中傳播時，存在一個3.36～8.26GHz頻率范圍的禁帶。

線偏振平面波沿垂直于磁化方向入射到YIG時，也將分解為兩組本征波。分別是沿方向偏振的非尋常波TE波和垂直于方向偏振的尋常波TEM波，它們對應的相對磁導率μIr，⊥和μIIr，⊥分別為

μIr，⊥的頻率頻率響應特性如圖2所示。

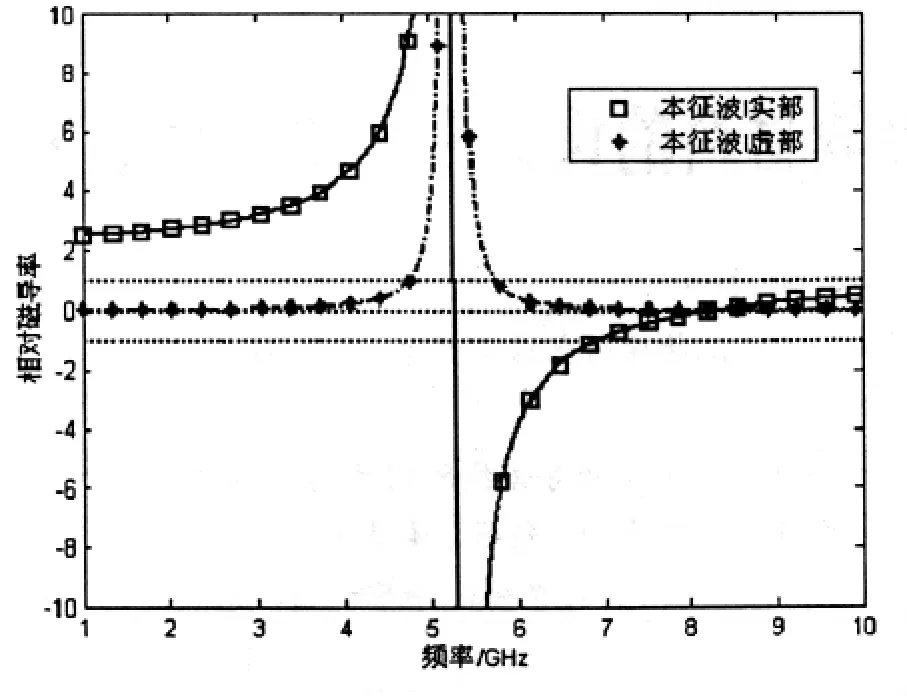
圖2 垂直于磁化方向入射時，本征波I的相對磁導率的頻率響應特性

由圖2可知，該本征波相對磁導率數值在頻率5.22～8.33GHz范圍內為負數。

μIr，⊥的頻率頻率響應特性曲線中相對磁導率的兩個零點隨飽和磁化強度M0和外加磁場強度H0的變化情況如圖3和圖4所示。

圖3 μIr，⊥的頻率響應特性曲線的兩個零點隨飽和磁化強度M0的變化情況

圖4 μIr，⊥的頻率響應特性曲線的兩個零點隨外加磁場強度H0的變化情況

由圖3和圖4可知，零點頻率值隨飽和磁化強度M0的增大而增大，磁導率為負的頻率帶寬也隨飽和磁化強度M0的增大而增大;零點頻率值隨外加磁場強度H0的增大而增大，磁導率為負的頻率帶寬幾乎不受外加磁場強度H0的影響。

二、金屬導體線周期陣列結構的等效介電常數

一維金屬導體線周期陣列結構和三維金屬導體線周期陣列結構分別如圖5和圖6所示。

圖5 一維金屬導體線周期陣列結構

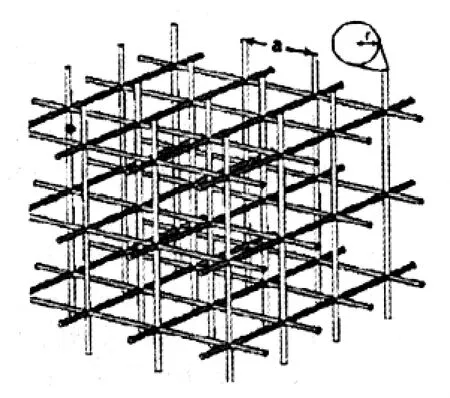
圖6 三維金屬導體線周期陣列結構

根據Pendry的理論［3］，一維金屬線陣列可以等效為具有等離子頻率的電介質，其等效的介電常數為:

三、亞鐵磁材料基片中嵌入金屬導體線周期陣列的結構模型及電磁特性分析

根據上述的原理，將圖6所示的三維金屬導體線周期陣列結構嵌入到圖7所示的YIG基體中構成復合電磁特異材料，且可以被看作是一種有效媒質。媒質A為三維金屬導體線周期陣列結構，物理參數為a=2mm、r=0.15mm。媒質B為YIG，其物理參數如前所述。利用有效媒質理論的MGa模型［12］。

圖7 電磁波在YIG中傳播的模型

其中fa、εa、μa分別為媒質A的體積分數、介電常數和磁導率;εb、μb分別為媒質B的介電常數和磁導率;ε、μ分別為復合媒質的介電常數和磁導率，其中fa遠小于1。可以得到如下解析式:

電磁波沿平行于磁化方向傳播時，YIG中本征波I對應的等效磁導率為

電磁波沿平行于磁化方向傳播時，YIG中本征波I對應的等效磁導率為

數值計算結果如圖8～11所示。

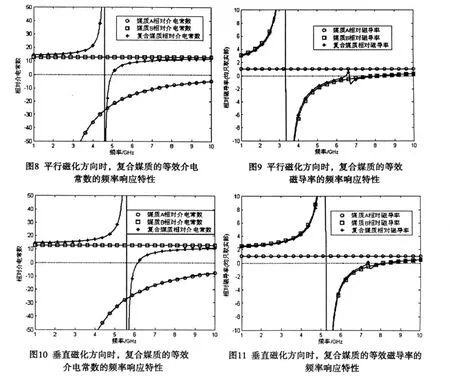
對照圖8、9可知，存在C波段電磁波頻率的重疊區域，使得復合媒質的等效介電常數與等效磁導率同時為負。由計算結果可知，復合媒質的等效介電常數在5.587～6.149 GHz頻段內為負，等效磁導率在5.269～7.332 GHz頻段內為負，同樣存在C波段電磁波頻段的重疊區域，使得復合材料的等效介電常數與等效磁導率同時為負。

四、結語

本文分析了亞鐵磁材料－YIG實現負磁導率，金屬導體線周期陣列結構實現負介電常數的機理及參數條件;通過將金屬導體線周期陣列結構嵌入YIG基體中構成復合電磁特異材料，利用有效媒質理論數值計算了復合電磁特異材料的等效介電常數與等效磁導率的頻率響應特性。結果表明，存在使得復合媒質的等效介數常數與等效磁導率同時為負的電磁波頻段，表明了利用有效媒質理論可以基于亞鐵磁材料設計負折射率特異材料。

［1］Veselago V G.The electrodynamics of substances with simultaneously negative values of ε and μ［J］.Soviet Physics Uspekhi，1968，10(4):509－514.

［2］Smith D R，Padilla W J，Vier D C，et al.Composite medium with simultaneously negative permeability and permittivity［J］.Phys RevLett，2000，84(18):418.

［3］Pendry J B，Holden A J，Robbins D J，et al.Low frequency plasmons in thin－wire structures［J］.J Phys:Condensed Matter，1998，(10):4785.

［4］Gokkavas M，Guven K，Penciu R S，et al.Experimental demonstration of a left－handed metamaterial operating at 100 GHz［J］.Phys Rev B，2006，73(19):193103.

［5］Chen H，Ran L，Huangfu J，et al.Negative refraction of a combined double S－shaped metamaterial［J］.Appl Phys Lett，2005，(86):1.

［6］Chen Hongsheng，Ran Lixin，Jin Au Kong，et al.Left－handed materials composed of only S－shaped resonators［J］.Phys Rev E，2004，70(5):57－65.

［7］Lagarkov A N，Semenenko V N，Kisel V N，et al.Development and simulation of microwave artificial magnetic composites utilizing nonmagnetic inclusions［J］.J Magn Magn Mater，2003，(161):258.

［8］Caloz C，Itoh T.Transmission line approach of left－handed(LH)materials and microstrip implementation of an artificial LH transmission line［J］.IEEE Trans Antennas Propagation，2004，52(5):1159.

［9］Eleftheriades G V，Iyer A K，Planar P C.Planar negative refractive index media using periodically L－C loaded transmission lines［J］.IEEE Transactions on Microwave Theory and Techniques，2002，50(12):2702.

［10］Pimenov A，Loidl A，Przyslupski P，et al.Negative refraction in ferromagnet－supercond－uctor superlattices［J］.Phys Rev Lett，2005，95(24):247009.

［11］He Yongxue，He Peng，Vincent G Harris，et al.Role of ferrites in negative index metamaterials［J］.IEEE Trans Mag，2006，42(10):2852.

［12］V B Bregar，M Pavlin.Effective－susceptibility tensor for a composite with ferromagnetic inclusions:Enhancement of effective－media theory and alternative ferromagnetic approach［J］.Journal of Applied Physics，2004，95(11):6289－6293.

2011－01－09

湖南省科技計劃資助項目(2010gk3160);湖南省高等學校科學研究資助項目(10C0314)

鄧躍龍(1964－)，男，湖南益陽人，高級講師。