一般位置直線段實長及傾角講解方法的探討

胡少興 張愛武 劉靜華 王運巧

1北京航空航天大學機械工程及自動化學院，北京 100191

2首都師范大學三維信息獲取與應用教育部重點實驗室，北京 100037

一般位置直線段實長及傾角講解方法的探討

胡少興1張愛武2劉靜華1王運巧1

1北京航空航天大學機械工程及自動化學院，北京 100191

2首都師范大學三維信息獲取與應用教育部重點實驗室，北京 100037

從觀察日常生活中諸多部件或零件開始，引出一般位置直線實長及其對投影面傾角求解的必要性，給出由投影求出一般位置直線的實長及其對投影面傾角及直線與投影軸夾角的方法，總結實長、傾角和夾角的求解規律。而后通過幾個典型習題的作圖過程分析，加深學生對定理的理解。幾輪講述表明：采用該種形式學生不僅能夠快速掌握直角三角形法，而且也能激發學生學習工程制圖的興趣。

一般位置直線；直角三角形法；實長；傾角；夾角

General location line; Right triangle method; Length; Obliquity; Angle

在日常生活中，同學們看到的聯通信號塔、體育館的屋頂、電視塔等等都是根據我們講述的制圖基本知識繪制的工程圖紙加工出來的。這些物體無論選擇哪個方向投影，在其工程圖上，都會出現許多在三個投影面上的投影均呈類似性，既不能反映該線段的實長，也不能反映該線段對投影面傾角的一般位置直線。因此在施工過程中，必須求出實長，才能進行加工。這樣不僅節省材料，而且可以加快施工速度。類似的一般位置直線的例子在機電產品的設計過程中出現的頻率更是數不勝數，所以對于一般位置直線，我們必須求出實長。

對于一般位置直線，求其實長及其對投影面的傾角有直角形法或換面法[1～2]。對于這兩種方法，換面法比較簡單，這里著重介紹直角三角形法。對于該種方法，目前的教材[3~5]都是按照相同的方式進行講述，并沒有對其進行深入分析。本文根據作者的理解，給出由投影求出一般位置直線的實長及其對投影面傾角及直線與投影軸夾角的方法，并對實長、傾角和夾角的求解規律進行總結。

一、 直角三角形法

為了更加直觀的理解一般位置直線在三個投影面的投影特性，同學們可以將三個投影面理解成教室中由地面（相當于H面）、側墻面（相當于W面）和前墻面（相當于V面）組成。其中地面和側墻面的交線為OY軸，地面和前墻面的交線為OX軸，側墻面和前墻面的交線為OZ軸，一般位置直線就相當于在這三個投影面中的投影。下面我們在該三個投影面組成的立體空間中，分別講述空間直線的實長及對各投影面傾角的求法。

例1：求空間直線AB的實長及對H面的夾角α。

解：求解過程見圖1。

我們知道，直線由兩點確定，要作直線的投影，實質就是作出線上兩點的投影，也就是說，它的投影由直線上兩點的同面投影的連線來確定。由此得到直線AB的V投影a＇b＇和H面的投影ab，其中ab垂直Bb。過A點作AA1平行于ab，則AA1垂直于Bb，由此得一直角三角形BAA1。

在該三角形中∠A1AB為空間直線AB與H面所成的傾角，定義為α；該角所對的直角邊為空間直線AB的Z坐標差，另一條直角邊為直線AB在H面投影ab。斜邊是直線AB的實長，該角的余角為空間直線與Z軸的夾角。可見求實長、傾角及夾角最主要的問題是找到對應的直角三角形。

例2：求空間直線AB的實長及對V面的夾角β。

解：求解過程見圖2。

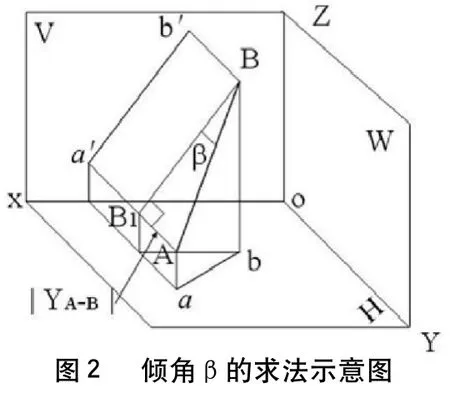
從圖中看出：對應的直角三角形為B1BA。在該三角形中，∠B1BA即空間直線AB與V面所成的夾角，定義為β；該角所對的邊為空間直線AB的Y坐標差，另一條直角邊為直線AB的V投影a＇b＇的長度。斜邊是直線AB的實長，該角的余角為空間直線與Y軸的夾角。可見求實長、傾角及夾角最主要的問題仍是找到對應的直角三角形。

例3：求空間直線AB的實長及對W面的夾角?。

解：求解過程見圖3。

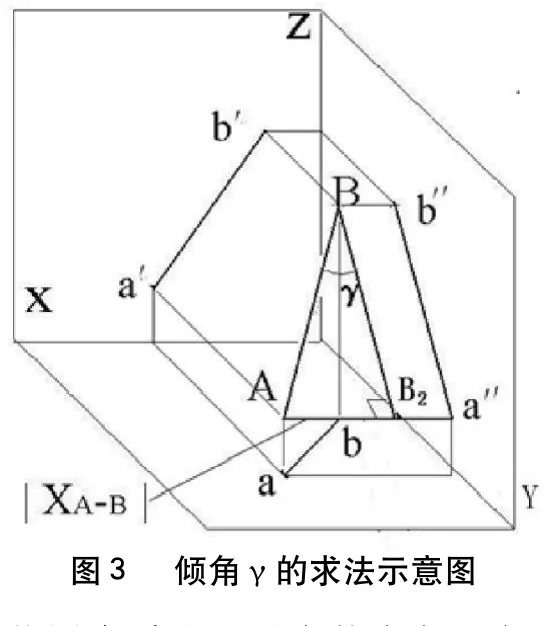
從圖中看出：對應的直角三角形為B2BA。在該三角形中，∠B2BA即空間直線AB與W面所成的傾角，定義為?；該角所對的邊為空間直線AB的X坐標差，另一條直角邊為直線AB的W投影a’b’的長度。斜邊是直線AB的實長，該角的余角為空間直線與X軸的夾角。可見求實長及夾角最主要的問題也是找到對應的直角三角形。

綜上所述，借助于直角三角形，就可以用圖解法求出線段AB的實長和與投影面的傾角。這種方法稱之為“直角三角形法”。

用直角三角形法求線段實長及傾角時，特別要注意傾角與兩直角邊一定是與同一投影面發生關系。直角三角形的構成圖將這種關系表達得十分清晰。用直角三角形法求實長及對投影面的夾角總結如下：

（1）求直線的實長及對H面的傾角。首先找出空間直線的Z坐標差和直線的水平投影，然后由這兩條邊組成直角三角形，Z坐標差這條直角邊所對應的角度為空間直線與水平投影面所成的傾角，另一條直角邊所對的角度為空間直線與Z軸所成的角，斜邊為實際長度；

（2）求直線的實長及對V面的夾角。首先找出空間直線的Y坐標差和直線的正面投影，由這兩條邊組成直角三角形，Y坐標差這條直角邊所對的角度為空間直線與正立投影面所成的傾角，另一條直角邊所對的角度為空間直線與Y軸所成的角，斜邊為實際長度。

（3）求直線的實長及對W面的夾角。首先找出空間直線的X坐標差和直線的側立投影，由這兩條邊組成直角三角形，X坐標差這條直角邊所對的角度為空間直線與側立投影面所成的傾角，另一條直角邊所對的角度為空間直線與X軸所成的角，斜邊為實際長度。

二、典型習題

由直角三角形的構成可知，該部分內容涉及四個基本作圖問題：

已知直線的兩投影，求直線與投影面的夾角和線段的實長；

已知直線的一投影及其與投影面的夾角，求直線的投影；

已知線段的一投影及其實長，求線段的投影；

已知線段的實長及其與投影面的夾角，求直線的投影。

其中第3和4可以合成一種情況，下面我們以習題方式進行講述，以加深學生對該方法的理解。

習題1 已知直線AB的兩投影，見圖4，求直線AB對V面的傾角和線段的實長。

解：有兩種解法，求解過程見圖4。

方法一：在H投影面上作圖，這里直線AB的水平投影已知，可以直接得到Y坐標差。過b點作OX軸的平行線，與a＇a相交與m，則ma的長度為Y坐標差，延長使mn=a＇b＇，連接na，得直角三角形nma、。這里na為AB的實長，直角邊ma所對的夾角為空間直線AB與V面所成的傾角β。

方法二：在V投影面上作圖，過a＇做直線a＇k垂直于a＇b＇，并使a＇k=am，連接kb＇，同樣可得直角三角形，三角形的各邊及角度含義同法一。

習題2 已知線段CD=45mm及水平投影，求其正面投影。

分析：由已知條件，由于直角三角形的斜邊已知、一直角邊已知，可得直角三角形。另一直角邊即為兩端點對H面的距離之差△Z，從而可以求出V面投影，求解過程如圖5。

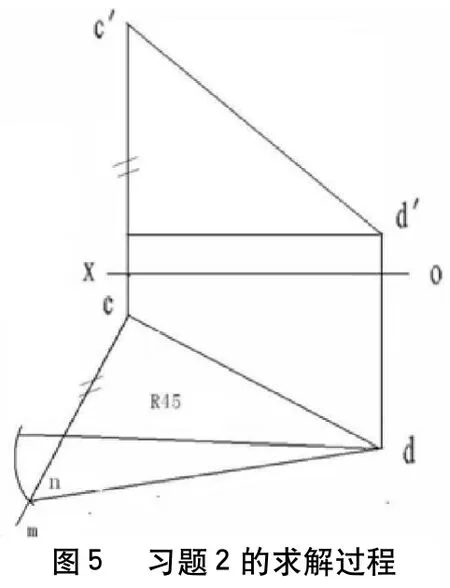
作圖步驟：

（1）以cd為一直角邊，過c點作一直線cm垂直于cd；

（2）以d點為圓心，以45為半徑，作一圓弧與直線cm相交于n點，得直角三角形，cn的長度即為空間直線CD的Z坐標差；

（3）根據投影關系，得到直線CD正面投影，即c＇d＇。

習題3 已知直線AB的投影a＇b＇，與V面的傾角β=30°，求其水平投影。

分析：由直角三角形的構成圖可知，若傾角為β，則該直角三角形的兩條直角邊一定是線段在V面的投影和兩端點對V面的距離之差。a＇b＇已知，傾角已知，該直角三角形可以得到。另一直角邊即為兩端點對V面的距離之差△Y，從而可以求出H面投影，求解過程見圖6。

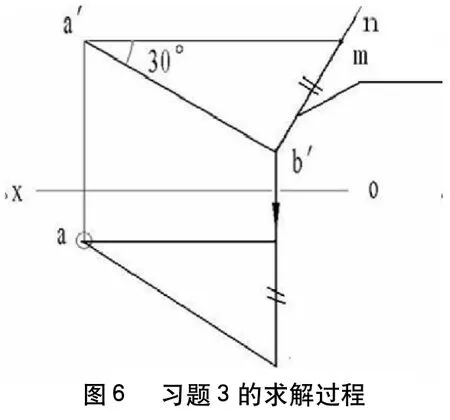
作圖步驟：

（1）首先，過b＇作一直線b＇n垂直于a＇b＇；

（2）過a＇點作與a＇b＇成300的直線，與直線b＇n交于m點，則b＇m即為△Y；

（3）根據投影關系，得到直線AB水平投影，即ab。

三、結論

以學生為中心，發揮學生的想象空間，從日常生活中所見到的一些事物開始，探討求一般位置直線實長及其對投影面傾角求解的必要性，總結實長、傾角和夾角的求解規律。即在投影圖上求線段的實長和傾角的方法是：以線段在某個投影面上的投影為一條直角邊，以線段的兩端點到該投影面的距離差為另一條直角邊作直角三角形，該直角三角形的斜邊就是所求線段的實長，而此斜邊與投影的夾角，就是該線段對該投影面的傾角。

[1]黎孟珠,石相莉.用換面法與直角三角形法求一般位置平面實形的比較.桂林航天工業高等專科學校學報[J].2006;(2):13～14

[2]楊衛紅.直角三角形法求作直線實長和投影的應用.山西建筑[J].2005;31(8):16～17

[3]何銘新,千克強.機械制圖[M].第四版.北京：高等教育出版社.1997

[4]朱淑芳,蔡雨林.機械制圖[M].西安:西北工業大學出版社.1992

[5]李澄,吳天生,聞百橋.機械制圖[M].北京:高等教育出版社.1996

A novel instruction way for solving general line’s length and its obliquity angle between projection planes

HU Shaoxing1ZHANG Aiwu2LIU Jinghua1WANG Yunqiao1
1.School of Mechanical Engineering and Automation, Beihang University, Beijing 100191,China; 2. Ministry of Education Key Laboratory of 3D Information Acquisitionand Application,Capital Normal University, Beijing 100037,China

Basing on numerous observation of many mechanical parts and components, the importance of solving general line’s length and its obliquity angle between projection planes is discussed. A novel method for solving general line’slength and its angles between projection planes and projection axle is proposed. A generalized method for solving space line’s length and its angles between projection planes and axles is also given. Author’s teaching experiments indicate that this method can not only make students understand and master right triangle method but also can stimulate students’ interests of engineering drawing.

O221

A

10.3969/j.issn.1001-8972.2011.16.123

胡少興(1972~),男,副教授,博士。主要研究方向三維激光、逆向工程及智能控制等。