基于單片FPGA的諧振式光纖陀螺數字系統設計與實現

姚靈芝，馬慧蓮，金仲和

(浙江大學信息與電子工程學系，杭州 310027)

諧振式光纖陀螺(Resonator Fiber Optic Gyro，RFOG)是一種基于Sagnac效應的高精度新型傳感器，其敏感器件光纖環形諧振腔(Fiber Ring Resonator，FRR)可以采用很短的光纖或集成光學的方法實現，因而在小型化和集成化上具有獨特的優勢［1－2］。由于Sagnac效應是一種極其微弱的效應，信號檢測技術在RFOG中占有重要的地位。相比于模擬電路，基于數字電路的檢測系統具有穩定性好、抗干擾能力強、處理速度快和體積小等優勢。因此，系統的數字化是RFOG向高精度和小型化發展的必經之路。

本方案以單片現場可編程門陣列(Field Programmable Gate Array，FPGA)為核心硬件單元，利用調相譜檢測原理［3］，設計了基于正負斜率組合鋸齒波相位調制的諧振式光纖陀螺全數字閉環處理系統，包括調制信號的產生、信號的同步解調以及數字反饋控制等功能。重點實現了基于比例積分(Proportion Integration，PI)控制技術的諧振頻率伺服回路、相位調制器(Phase Modulator，PM)的復位電壓漂移補償回路和第二閉環反饋控制回路。三個回路的設計和實現，使諧振式光纖陀螺在鎖頻精度、檢測精度和動態范圍等方面得到一定的提高和改善。另外，以前的PM復位電壓漂移補償回路和第二閉環反饋控制回路方案都是在開環檢測系統的基礎上通過增加儀器或器件來實現的，增加了整個檢測系統的復雜程度和體積。而本方案將整個檢測系統集成到單片FPGA中，為諧振式光纖陀螺的小型化和集成化提供了一條技術途徑。

1 RFOG基本原理

RFOG是基于Sagnac效應的光學傳感器，通過檢測由Sagnac效應引起的非互易諧振頻率差測量旋轉角速度［1］。基于正負斜率組合數字鋸齒波相位調制技術的諧振式光纖陀螺系統結構如圖1所示。

圖1 正負斜率組合數字鋸齒波調制的RFOG系統框圖

鋸齒波相位調制的方式可以等效為對輸入到相位調制器的激光中心頻率進行移頻［4］，利用正負斜率組合鋸齒波的相位調制，可以實現雙頻率調制效果。系統中所用光纖均采用保偏光纖，光纖激光器(Fiber Laser，FL)的中心波長和線寬分別為1550 nm和50 kHz。由FL輸出的激光經光纖耦合器C1后被分成功率相等的兩束光波，分別通過LiNbO3相位調制器PM1和PM2，由正負斜率組合的數字鋸齒波進行相位調制后進入FRR，形成順時針(Clockwise，CW)和逆時針(Counter Clockwise，CCW)方向的兩束諧振光波，最后分別由光纖環形器CIR1和CIR2耦合到光電探測器(Photodetector，PD)PD1和PD2。根據光電探測器輸出光強與諧振頻率偏差的關系［5］，PD探測到的信號經過FPGA進行信號處理，最終得到RFOG的旋轉角速度。

單片FPGA上實現的數字信號處理過程主要包括第一閉環、第二閉環和相位調制器復位電壓反饋控制環路。第一閉環是通過比例積分反饋將激光器中心頻率鎖定在諧振腔CCW路的諧振頻率之上，減小由于激光器中心頻率和諧振腔諧振頻率波動造成的影響。第二閉環首先依據Sagnac效應產生的CCW和CW路的諧振頻率偏差產生等效移頻鋸齒波調制信號，通過將該調制信號疊加于原先施加在PM2上的正負斜率組合鋸齒波上，從而跟蹤鎖定CW路的諧振頻率，等效移頻鋸齒波信號即比較器輸出端可反映RFOG的轉動信息。根據光纖環形諧振腔對不同復位電壓的響應特性［6］，相位調制器復位電壓反饋控制回路通過PI反饋控制將復位電壓控制在相位調制器的全波電壓上，從而動態、實時實現CW和CCW環路的最佳載波抑制。

2 全數字化RFOG系統設計和實現

2.1 諧振頻率伺服回路

諧振式光學陀螺的調制解調方式必須至少鎖定其中一個方向傳播的光波，利用頻率伺服回路使激光器的輸出光頻率始終處于諧振狀態，通過間接探測另一方向傳播光波與激光器的頻率差得到RFOG的旋轉角速度。頻率跟蹤鎖定技術將直接影響陀螺的實際檢測精度。在圖1所示RFOG系統中，鎖相放大器(Lock-in Amplifier，LIA)LIA1解調輸出諧振腔CCW方向光波，經PI控制器后反饋控制激光器中心頻率，使得激光器中心頻率跟蹤鎖定諧振腔CCW方向光波諧振頻率。與基于一階慣性環節實現的激光器頻率跟蹤鎖定方案相比［7］，基于PI控制器的諧振頻率伺服技術，有利于消除鎖定殘差和提高鎖頻環路的精度［8－9］。

PI控制器通過對誤差信號e(t)進行比例和積分運算，并將運算結果進行加權相加得到控制器的輸出u(t)，其數學表達式可以表示為:

式中u(t)為PI控制器的輸出信號，e(t)為輸入誤差信號，Kp為比例系數，Ti為積分時間。

對式(1)進行離散化，以求和運算代替積分運算后可在FPGA中實現全數字PI控制器。

將激光器中心頻率鎖定在光纖環形諧振腔諧振頻率上后，觀察鎖相放大器輸出信號。如圖2所示，在500 s內輸出信號的波動約為5 mV，信號的波動即反映鎖定環路的控制精度［8］。根據實際系統測試得到的標度因數為77.5 mV/(°/s)，可以計算得到對應角速度檢測精度約為8.7°/h。

圖2 CCW路鎖定后解調輸出信號

2.2 相位調制器復位電壓反饋控制回路

背向散射噪聲是RFOG的主要噪聲之一。T.J.Kaiser等人對背向散射噪聲進行了測試分析［10］，給出了計算腔內背向散射光波產生的陀螺輸出噪聲的經驗公式為:

式中c為真空中的光速;λ0為真空中的光源波長;N為載波抑制的個數，N=0、1、2分別表示CW/CCW環路沒有施加載波抑制、其中一路施加載波抑制以及雙路同時施加載波抑制;D為FRR的直徑;L為FRR的光纖長度;σ表示FRR腔內等效散射系數，可以通過對諧振腔背向散射特性進行具體測試獲得［11］;ΔV=Va－Vopt，其中Va表示施加在相位調制器上的調制電壓幅度，Vopt表示最佳載波抑制時所對應的最佳調制電壓幅度值，(ΔV/Vopt)表示載波抑制比。

為了避免在PD輸出端引入背向散射噪聲，需要對載波分量進行抑制。基于正負斜率組合鋸齒波調制的光場，其載波分量的表達式為:

式中M=π·Va/Vπ為調相系數，Va為鋸齒波電壓幅度(即復位電壓的一半)，Vπ為相位調制器的半波電壓。

根據式(3)，從抑制背向散射引入的噪聲出發，當調相系數M=π時，載波分量A0=0，此時載波幅度Va等于相位調制器半波電壓Vπ。另外，為了實現鋸齒波的線性相位調制，同樣需要載波電壓等于相位調制器的半波電壓［6］。利用自外差系統測試光載波抑制比與相位調制器上調制電壓間的關系［12］，結果如圖3所示。實測的載波抑制比與理論值基本吻合，而在最佳調制指數(M=π)附近發生偏差，這可能是由測試系統背景光功率波動及測試光源頻率噪聲等因素引起。由圖3可知，通過調整鋸齒波復位電壓比較容易實現45 dB的載波抑制比。考慮到實際LiNbO3相位調制器半波電壓隨溫度的變化率約為 500×10－6V/℃［13］，溫度變化時，正負斜率組合鋸齒波不精確的復位電壓施加到相位調制器上會給系統引入附加噪聲［14］。這就需要設計反饋控制回路使加載在PM上調制波形的復位電壓動態、實時保持在調制器全波電壓數值上。

圖3 鋸齒波調制指數與光載波抑制比關系

考慮到實際鋸齒波復位時間不為零，因此FRR輸出光場存在對復位信號的瞬態響應過程，且FRR產生的瞬態響應和拖尾信號特性依賴于復位電壓［8］。以鋸齒波調制頻率為參考頻率對不同復位電壓下的拖尾進行方波同步解調，得到如圖4所示的結果。可以看到，當調制電壓峰峰值(2Va)在5.75 V～6.15 V變化時，解調輸出信號與調制電壓峰峰值成近似線性關系，并且當調制電壓峰峰值為5.92 V時，解調輸出信號為0，因此該相位調制器的全波電壓(2π電壓)為5.92 V。利用解調輸出信號和調制電壓峰峰值的線性關系以及解調輸出零點，將拖尾的解調信號通過PI控制器處理后反饋到調制信號發生器的增益控制端，從而對施加在相位調制器上的正負斜率鋸齒波幅度進行實時反饋控制。初始復位電壓小于2π電壓和大于2π電壓的實驗結果如圖5所示。由圖可知，研制的反饋控制回路技術，經短暫振蕩后能夠將調制鋸齒波峰峰值較快鎖定到相位調制器的2π復位電壓上。

圖4 非理想鋸齒波2π復位電壓的解調輸出

圖5 不同復位電壓下反饋加入前后誤差信號輸出

2.3 第二閉環反饋控制環路設計

通過對PM調制波形進行反饋控制將激光頻率鎖定在CW路的諧振頻率上，稱之為第二閉環。這樣兩路激光鎖定在各自的諧振頻率上，從而可以得到反映陀螺轉動角速度的諧振頻差信號。第二閉環的加入能夠使陀螺始終工作在解調曲線零點附近的線性區，有利于增大陀螺信號的動態范圍，同時可有效抑制兩路互易性噪聲的影響。

第二閉環的原理是在PM上疊加一個等效移頻鋸齒波，該等效移頻鋸齒波斜率體現RFOG旋轉引起的Sagnac頻差信號，其結構如圖6所示。鋸齒波斜率由臺階持續時間τ和臺階高度step共同決定。在選定τ的情況下，通過改變臺階高度即可實現鋸齒波斜率的改變。將CW和CCW兩路解調信號通過比較器后，對鋸齒波的臺階高度作±1 LSB(DAC的最小改變量)的改變，這樣調制波形斜率變為±fm，CW±Δfs(Δfs為1 個 LSB 對應的頻率改變量)。通過對臺階高度量進行累加，得到移頻鋸齒波。再對比較器的輸出Δstep信號進行數字式積分，即可得到頻差信號為:

圖6 移頻調制光路模型

圖7 移頻測試曲線

在CCW路鎖定的情況下，將各種斜率不同的移頻鋸齒波分別疊加到正負斜率組合鋸齒波上，然后對光進行相位調制。觀察兩路解調信號的差值電壓變化，測試結果如圖7所示。可以看出，移頻鋸齒波的臺階高度每變化±1 LSB，輸出電壓信號變化±58.1 mV。根據實驗標度因數為 77.5 mV/(°/s)，且1°/s對應774 Hz頻差，單位移頻鋸齒波的等效移頻量為580.25 Hz。將陀螺系統放置于轉臺上，觀察加入反饋環路前后CW和CCW兩路解調差值信號的變化，實驗結果如圖8所示。可以看到，加入反饋回路后，信號鎖定到0附近，補償了因轉動引起的開環信號量，順利實現了閉環功能。

圖8 第二閉環模塊功能測試

3 系統測試

陀螺數字閉環系統以單片FPGA為核心進行設計，其框圖如圖9所示，主要包括調制波形發生器、數字鎖相放大器、PI控制器、相位調制器全波電壓控制、PM移頻控制、信號處理等模塊。根據實際測試結果，研制的諧振式光纖陀螺輸出信號的標度因數為77.5 mV/(°/s)。圖10為轉速為1°/s時，陀螺輸出信號測試結果。其中上面曲線為RFOG輸出信號，下面曲線為Analog Devices公司的MEMS陀螺ADXRS401(標度因數為15 mV/(°/s))的輸出信號。

在積分時間為30 s的情況下，對陀螺信號測試2 h，陀螺輸出如圖11所示，計算得到零偏穩定性為159.3°/h。該結果一方面受限于激光器頻率鎖定環路性能，激光器的中心頻率和諧振腔諧振頻率不穩定，微弱的Sagnac效應信號淹沒于激光器的頻率噪聲之中，雖然激光器頻率鎖定環路抑制了大部分的激光器頻率噪聲，但仍有殘余的波動引入到陀螺信號中;另一方面，溫度的波動導致FRR的兩個本征偏振態各自所對應的諧振光波發生疊加與干涉效應，引起諧振曲線的不對稱性和本征偏振態之間的干涉，導致諧振頻率點的檢測誤差，從而限制了RFOG的檢測精度。

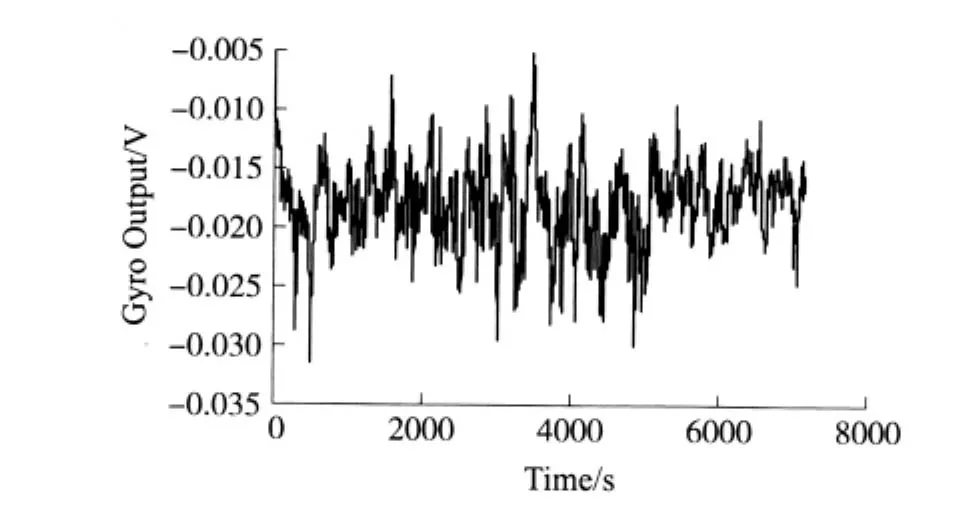
圖11 陀螺零偏穩定性測試

4 結語

RFOG相比于目前發展已經比較成熟的干涉式光纖陀螺，具有小型化方面的優勢，而數字信號檢測系統的精度直接影響陀螺的測試精度。本文基于正負斜率組合鋸齒波數字相位調制技術，設計了諧振式光纖陀螺雙閉環數字檢測系統。采用全數字信號處理技術，將整個陀螺檢測系統集成到單片FPGA中。通過測試，驗證了激光器閉環鎖定環路、2π電壓反饋控制環路和第二閉環功能的正確性，有利于諧振式光纖陀螺的小型化和集成化發展。后續工作中，將圍繞提高激光器頻率鎖定精度和第二閉環的精度、克服溫度變化引起的漂移等方面作進一步的研究，以提高FROG的檢測精度。

［1］Ezekiel S，Balsmo S K.Passive Ring Resonator Laser Gyroscope［J］.Appl.Phys.Lett.，1977，30(9):478－480.

［2］Ezekiel S.Optical Gyroscope Options:Principles and Challenges［J］.Optical Fiber Sensors，2006，paper MC1.

［3］張旭琳，馬慧蓮，周柯江，等.調相譜檢測技術下諧振式光纖陀螺實驗研究［J］.傳感技術學報，2006，19(3):800－803.

［4］Harumoto M，Hotate K.Resonator Fiber Optic Gyro Using Digital Serrodyne Modulation［J］.J.of Lightwave Technol.，1997，15(3):466－473.

［5］Hotate K，WANG Xi-jing，HE Zu-yuan.Resonator Fiber Optic Gyroscope with Digital Serrodyne Scheme Using a Digital Controller［J］.SPIE，2009，7314:02－01－02－08.

［6］Strandjord L K，Sanders G A.Effects of Imperfect Serrodyne Phase Modulation in Resonator Fiber Optic Gyroscopes［J］.SPIE，1994，2292:272－282.

［7］楊志懷，馬慧蓮，鄭陽明，等.諧振式光纖陀螺數字閉環系統鎖頻技術［J］.中國激光，2007，34(6):814－819.

［8］鮑慧強，毛慧，馬慧蓮，等.諧振式微型光學陀螺鎖頻精度分析［J］.浙江大學學報(工學版)，2010，44(1):94－98.

［9］楊雪峰，鄭陽明，馬慧蓮，等.諧振式光纖陀螺環路鎖頻技術研究［J］.傳感技術學報，2007，20(5):990－993.

［10］Kaiser T J，Cardarelli D，Walsh J.Experimental Developments in the RFOG［J］.SPIE，1990，1367:121－126.

［11］馬慧蓮，鮑慧強，王世軍，等.二氧化硅光波導環形諧振腔的背向散射特性研究［J］.中國激光，2010，37(1):105－109.

［12］MA H L，HE Z Y，Hotate K.Reduction of Backscattering Induced Noise by Carrier Suppression in Waveguide-Type Optical Ring Resonator Gyro［J］.J.Lightwave Technol.，2010，Digital Object I-dentifier:10.1109/JLT.2010.2092751.

［13］張維敘.光纖陀螺極其應用［M］.北京:國防工業出版社，2008:117－118.

［14］李如春，馬慧蓮，金仲和，等.數字調制諧振式光纖陀螺中階梯波復位誤差的分析［J］.中國激光，2007，31(9):1107－1111.