多維力傳感器耦合分析及解耦方法的研究*

曹會彬，孫玉香，劉利民，馮 勇，王以俊，葛運建，*

(1.中國科學院合肥智能機械研究所，合肥 230031;2.中國科學技術大學，合肥 230026)

多維力傳感器是機器人實現智能化應用最重要的傳感器之一［1－4］。根據應用的場合不同，能夠設計成不同維數(1維－6維)的傳感器，從而測量三維空間的全力信息(3個力分量和3個力矩分量)。由于力傳感器在機械設計中要求體積小，結構緊湊、功能強等特點，這同時也帶來了多維力傳感器的共性問題，即維間耦合問題。消除維間耦合是多維傳感器準確測量的核心，也是機器人實現智能化控制的重要前提［5－8］。

目前常用的傳感器靜態解耦的主要方法［9］:一是基于線性標定的靜態解耦算法。假設傳感器為線性系統的前提下，通過對六維力傳感器各方向進行實驗標定，進而確定標定矩陣。二是基于最小二乘法線性擬合的靜態解耦算法。根據最小二乘法，依據標定數據進行線性擬合，可得到廣義外力各分別單獨加載時，力分量與各電橋輸出電壓之間的線性回歸方程［10－11］。

對于多維力傳感器的解耦問題并沒有統一的處理方法，本文以我們研制的六維腕力傳感器為依托，提出了一種基于神經網絡的多維力傳感器的解耦方法［12］。通過對解耦后數據分析，證實了該方法解耦的可行性和優越性。這樣工程實現時可以大大提高機械手的控制精度，滿足機器人智能控制的要求。

1 多維力傳感器的耦合分析

多維力傳感器的耦合從產生的原因上分為兩種:結構性耦合和誤差性耦合。以我們研制的六維力傳感器為例，結構如圖1所示(六維力傳感器上膜測量三維力矩:Mx，My，Mz;下膜測量三維力:Fx，Fy，Fz)。

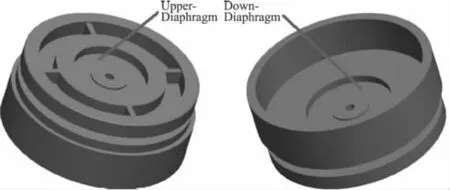
圖1 六維力傳感器結構圖

1.1 結構耦合

結構性耦合產生的原因主要是因為彈性體是一體化結構，在設計上某些方向必然存在耦合，例如Mx(繞X軸的力矩)與Fy(沿Y軸的受力)和My(繞Y軸的力矩)與Fx(沿X軸的受力)，其它方向是不存在這種耦合的，這些可以從有限元分析中得到。由于產生的原理相同，存在結構性耦合的以Mx和Fy為例，如圖1所示。不存在這種耦合的以Mz和Fx，Fz，Mx為例，如圖 2 所示。

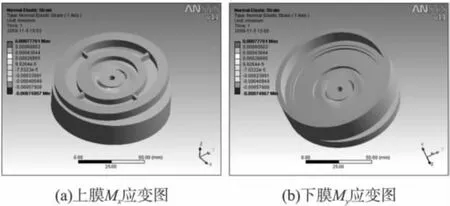
圖2 有限元分析圖Mx－Fy

從圖2(a)可以看出，在上膜施加力矩Mx時，在下膜Fy方向上有明顯的應變現象如圖2(b)所示。從圖3(a)可以看出，在上膜施加力矩Mz時，上膜和下膜沒有明顯的應變，如圖3(b)、3(c)、3(d)所示。

圖3 有限元分析圖Mz－Mx－Fx－Fz

1.2 誤差耦合

誤差性耦合產生的原因主要是制造工藝和貼片水平的限制，而誤差性耦合在有限元分析中是不存在的，事實上誤差性耦合幾乎存在于所有的多維力傳感器中。下面以研制的六維腕力傳感器為例進行分析。

在上膜My施加力矩，方法是同一種力矩施加5次，施加大小為0，6 kg×5 cm，12 kg×5 cm，18 kg×5 cm，其它五維經A/D轉換后的數值如表1所示，解耦前后各維數據如圖4所示。

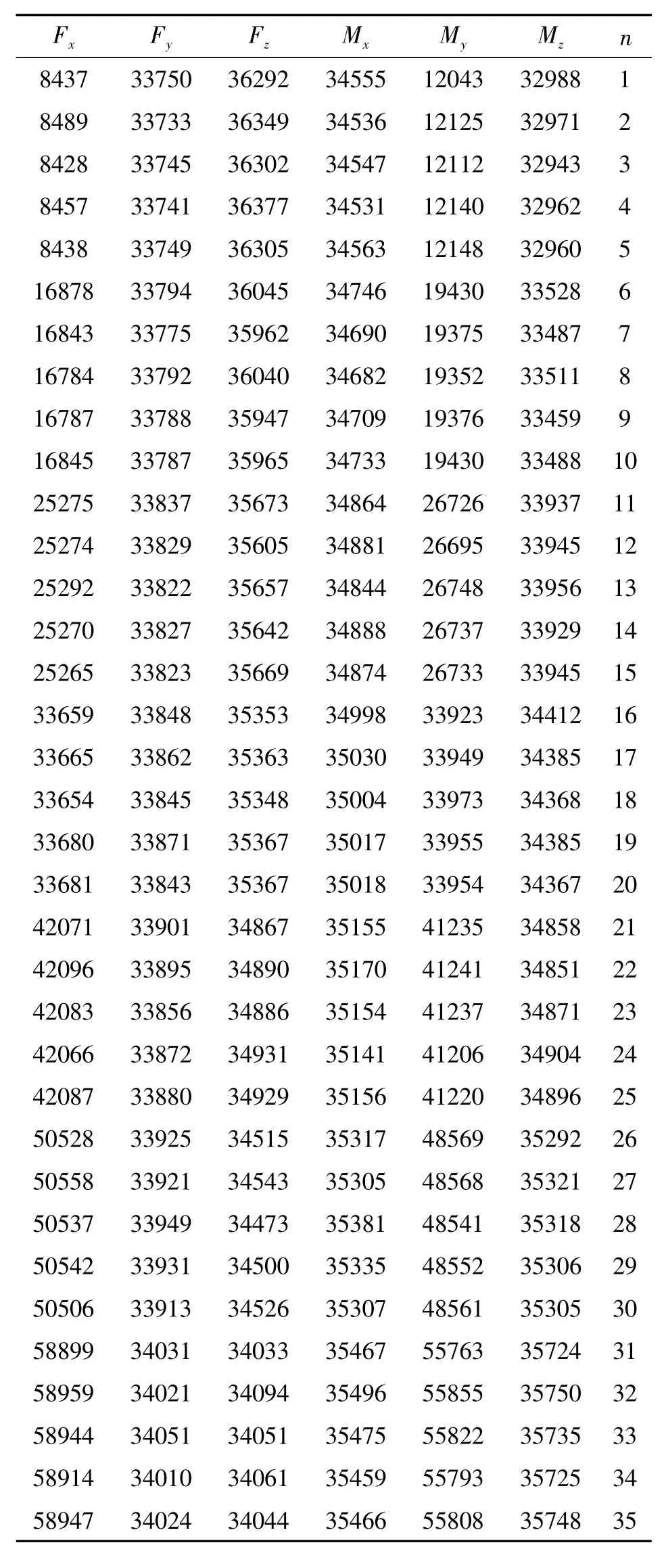
表1 沿X軸施加力測得數據

從表1數據可以看出施加力矩My時，其它五維都有不同程度的輸出。存在這結構耦合和誤差耦合現象。經過解耦以后，結構耦合和誤差耦合都有很大程度的提高，如圖4所示。

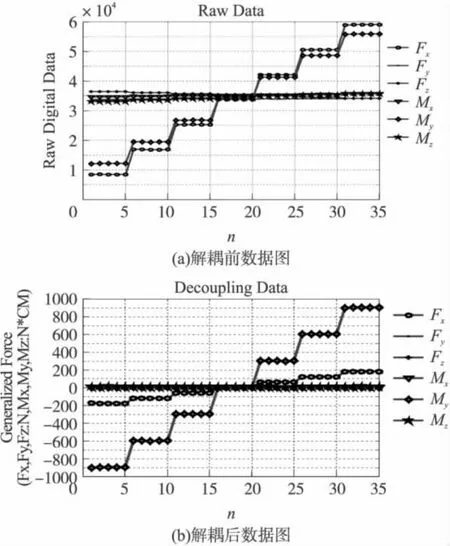
圖4 數據關聯示意圖

2 解耦方法研究

2.1 標定－樣本數據

神經網絡依靠學習樣本來確定網絡中的向量W值，一個學習樣本是一組輸入輸出數據。為了使經學習后得到的網絡具有更好的性能，也就是說能準確反映輸出量和輸入量之間的關系，所收集的數據必須包含問題的全部模式，所以我們采用的標定方法與文獻［5］相同。

為了確保標定－樣本數據的準確性和可靠性，在硬件設計上采用高精度的12位A/D采集的控制器和精密低噪聲放大器，軟件設計上采用數字低通濾波器(傳感器機械頻率120 MHz左右)和移動平均法的數據處理方式。

2.2 解耦－網絡訓練

六維腕力傳感器各維之間都存在著耦合，耦合的程度可以用網絡的權值來表示，如圖5所示。其中Nx，Ny，Nz，Nmx，Nmy，Nmz是在某一方向施加力或者力矩時，經過數據采集卡采集的原始數字量(采集范圍是0 ～4 095)，Fx，Fy，Fz，Mx，My和Mz是解耦后各維的真實受力數值，w(i，j)(1≤i，j≤6)是網絡訓練后的權值，表示第j維對第i維的影響程度，也就是耦合度。(1≤k≤6)為偏差矢量。

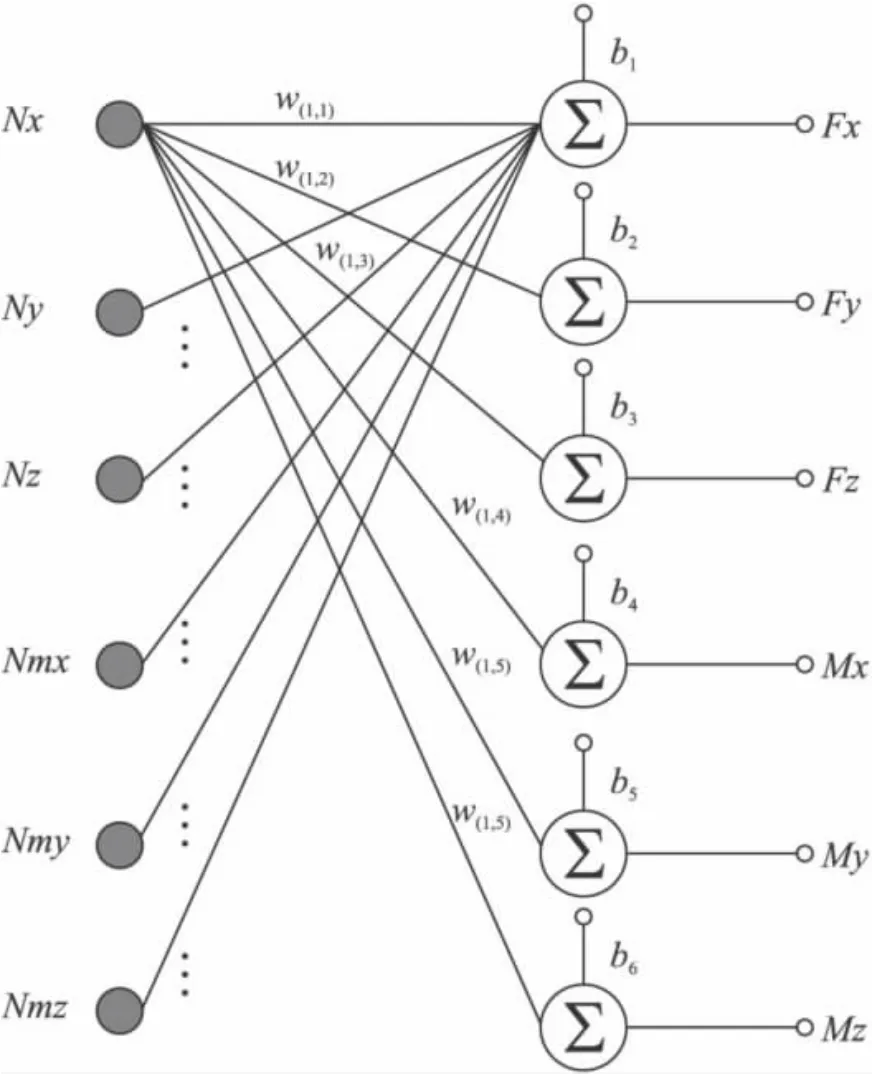
圖5 六維網絡訓練圖

在解耦之前通過標定得到加載力和采集數字量之間的關系為:

其中F表示各方向施加的標準廣義力(包括沿各軸的力和繞軸的力矩)，這里

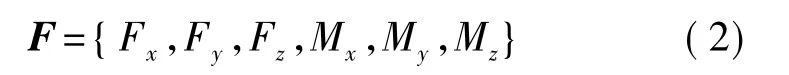
N表示通過數據采集卡采集到的數字量，這里

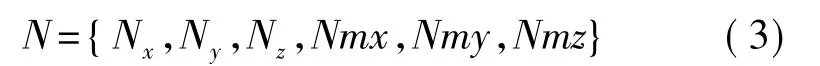
W是一個6×6的解耦矩陣，數據大小表示各維之間耦合的程度。其中主對角線w(i，j)(i=j，1≤i，j≤6)表示在某維單獨受力時力與標定數字量的相關系數，其它系數w(i，j)(i≠j，1≤i，j≤6) 表示第j維對第i維的影響程度，即耦合系數。

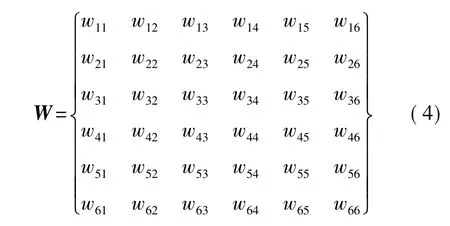
B是網絡訓練的偏移量:

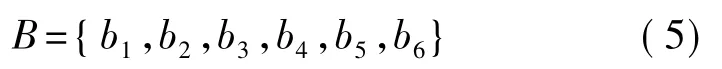
神經網絡解耦的優勢就是能夠把所有標定的有效數據進行訓練，得到一個最優的解耦矩陣。

解耦算法具體流程如圖6所示。

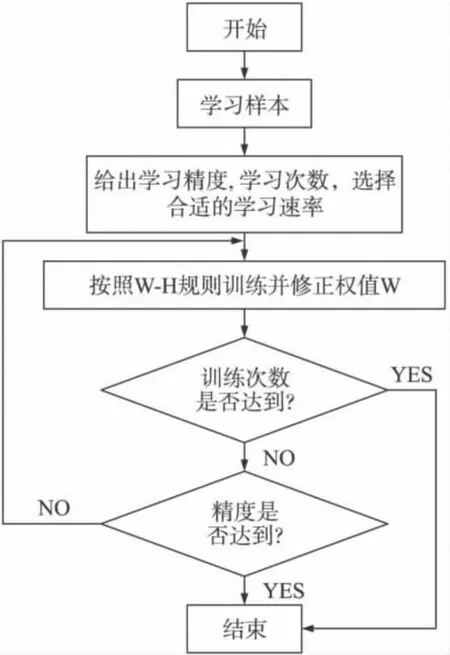
圖6 解耦算法流程圖

3 實例及分析

以我們研制的一款小量程的六維腕力傳感器為例，標定－樣本數據見附表1。標定過程以Mx為例如下:

(1)在上膜Mx施加力矩，力大小為6 000 g，力臂距離為5 cm，采集并且保存經過數據卡輸出的六路數字量，Fx，Fy，Fz，Mx，My和Mz，采集次數為5次。

(2)增加砝碼重量到12 000 g，力臂距離不變，采集并且保存經過數據卡輸出的六路數字量，Fx，Fy，Fz，Mx，My和Mz，采集次數不變。

(3)以此類推，最后完成實驗，獲得標定數據。其它維的標定過程與Mx相同。

獲取標定數據以后，根據3.2解耦－網絡訓練解耦算法，獲取解耦矩陣。在訓練過程中，網絡訓練次數不同，訓練的權值和偏差值不同，如下所示。

(a)訓練500次后的權值和偏差值

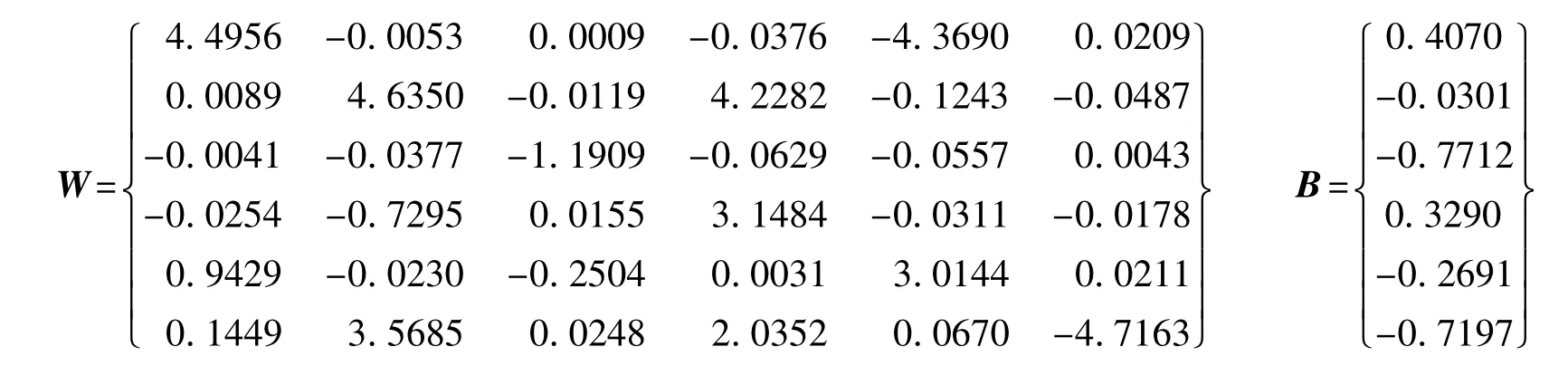
(b)訓練700次后的權值和偏差值

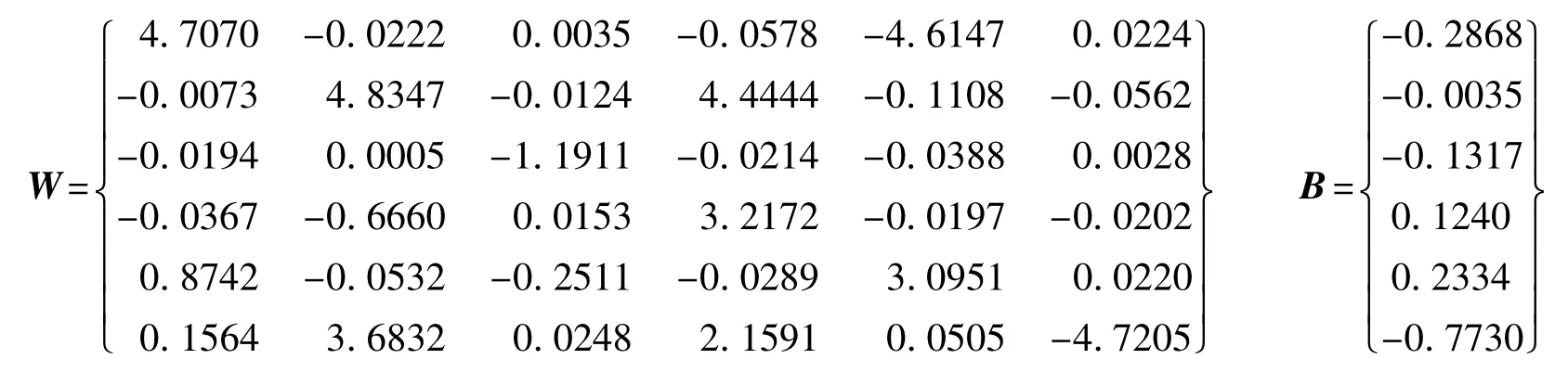
(c)訓練1 000次后的權值和偏差值

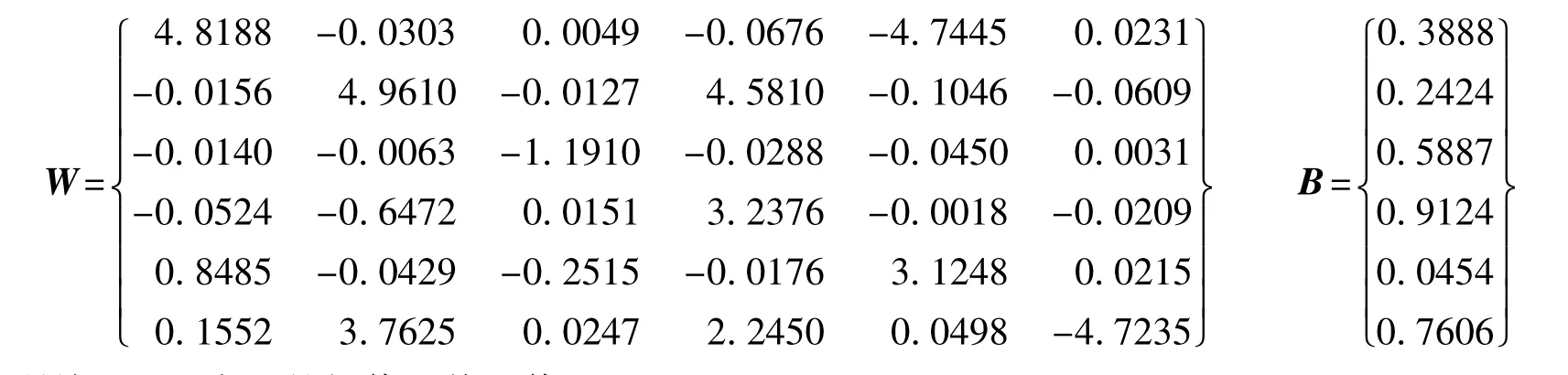
(d)訓練3 000次后的權值和偏差值

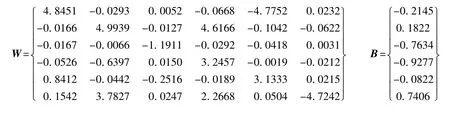
(e)訓練5 000次后的權值和偏差值

訓練后的誤差值也就不同。如表2所示。

表2 不同訓練次數的誤差和

由傳統靜態解耦方法［9］得到的方差和為sse=3.5641×105。由表2和表3可知，隨之訓練次數的增大，權值在變化，精度也在提高。以傳統解耦方法為基準點，訓練 500、700、1 000、3 000 和 5 000 后，方差和減少了 6.78%、21.23%、24.18%、24.34%、24.33%。總之只要在多維力傳感器誤差允許的范圍內，訓練的權值和偏差值都是有效的。

4 結論

力傳感器各維之間的耦合程度是由它的結構決定的。如何能夠定量的表示各維之間耦合程度是傳感器能夠應用的重要前提。本文提出的基于線性神經網絡解耦方法，是在準確獲取樣本數據的前提下，利用神經網絡的自適應性和學習性進行訓練得到網絡的權值和偏差值，也就是耦合矩陣。最后通過具體實例驗證了神經網絡訓練的優越性，對以后多維力的工程應用具有重要的指導意義。

［1］Yong Yu，Takashi Chaen，Showzow Tsujio.Hign-Stiffness and High-Sensitivity 3-Axis Force Sensor Using Strain=Deformation Expansion Mechanism，International Conference on Intelligent Robots and System J.Magn.Beijing，China，pp.4417－4422，October，2006，［Proceedings of the 2006 IEEE/RSJ］.

［2］Zang Xiaohui，Gao Fen.Design of New-Style Six-Dimension Force Sensors System for Robot Finger［J］.Journal of Transducer Technology，2003，22(9):22－25.

［3］Yao Zhihui，Zhang Fuxiang，Chen Hua.Novel Decoupled Six-Axis Robot Sensor［J］.Journal of Harbin Institute of Technology，2004，36(2):160－162.

［4］徐科軍，李成.多維腕力傳感器靜態解耦的研究［J］.合肥工業大學學報，1999，22(2):1－6.

［5］王建波，呂震中.基于INA的機器人六維腕力傳感器的解耦研究［J］.測控技術，2002，21(9):5－7.

［6］Jiang Zhaohui，Kohno M R.Robotic Manipulation of Flexible Objects Based on Vibration Control Using Force Sensors［C］//2002 IEEE International Conference on Systems，Man and Cybernetics，Hammamet，Tunisia，2002，4:6.

［7］Jianhe Lei，Liankui.Application of Neural Network to Nonlinear Static Decoupling of Robot Wrist Force Sensor［C］//Proceedings of the 6th World Congress on Intelligent Control and Automation，2006，pp.5282－5285.Martin T Hagan，Howard B Demuth，Mark Beale.Neural Network Design［M］.Beijing:China Machine Press，2002.8.

［8］Tommy C P Lo，Philip C H Chan.Design and Calibration of a 3-D Micro-Strain Gauge for in Situ on Chip Stress Measurements［C］//IEEE，ICSE’96 Proc.，1996:252－255.

［9］張景柱，郭凱.六維力傳感器靜態解耦算法應用研究［J］.傳感器與微系統，2007，26(12)58－62.

［10］LI Minggang.Calibration and Linerarization Method for Microcontroller—Based Sensor System［J］.Measurement＆ Control，1996，29(1):75－78.

［11］許德章，吳仲城，葛運建，等.機器人六維腕力傳感器耦合矩陣的確定與攝動分析［J］.儀器儀表學報，2005，26(1):7－11.

［12］叢爽.MATLAB工具箱的神經網絡理論與應用［M］.中國科學技術大學出版社，2003.