大輸出微控制力矩陀螺的設計*

常洪龍，白 濱，焦文龍，謝建兵，秦子明，苑偉政

(西北工業大學微/納米系統陜西省重點實驗室，西安 710072)

控制航天器姿態的執行機構有噴氣執行機構、飛輪、磁力矩器和重力桿等。控制力矩陀螺(Control Moment Gyroscope，CMG)屬于飛輪的一種，其基本工作原理是根據角動量守恒原理，依靠飛輪(即CMG中的轉子)和航天器(即CMG中的框架)之間的角動量交換實現輸出力矩的目的［1］。和其他幾種執行機構相比，CMG能夠精確連續地輸出力矩，具有功耗低、無污染、壽命長、高穩定性及指向精度高等優點［2－3］。

傳統的CMG輸出力矩可達到100 Nm～1000 Nm［4］，但因質量太大，通常在幾十到上百千克之間，并不適用于微米衛星、納米衛星等微小型航天器。而基于微機電系統(MEMS)技術的微控制力矩陀螺(Micro Control Moment Gyroscope，MCMG)具有傳統CMG的功能，同時降低了體積、重量和功耗等指標，并且相比于微推進器技術［5－6］，不存在燃料耗盡的問題。美國華盛頓大學的Reiter等人提出了一種微控制力矩陀螺的方案，其設計輸出力矩為2.3×10－12Nm［7］。如此小的控制力矩是MCMG本身尺寸小所帶來的固有特點，也是阻礙MCMG在微小型航天器上應用的重要因素。

本文提出了一種新型MCMG的設計方案，對其結構設計、寄生力矩消除、工藝實現等問題進行了分析，單個 MCMG的控制力矩輸出可達1.28×10－6Nm，相比于Reiter等人的設計，其輸出力矩增加了56萬倍，通過陣列組合有望得到更大的力矩輸出，增強小衛星的敏捷性［8］，在微小航天器的姿態控制中得到實際應用。

1 結構方案及工作原理

微控制力矩陀螺(MCMG)與微機械振動式陀螺(Micro Coriolis Vibratory Gyroscope，MCVG)一樣，都是利用科氏效應［9］。不同的是MCVG是利用科氏效應來敏感輸入角速率，是一個傳感器，而MCMG則利用科氏效應來輸出控制力矩，是一個執行器。

圖1為一個典型的傳統控制力矩陀螺的原理圖。轉子的轉動形成沿x軸的動量矩h，若框架帶動轉子繞z軸以速率δ進動，沿y軸就會輸出一個力矩N。

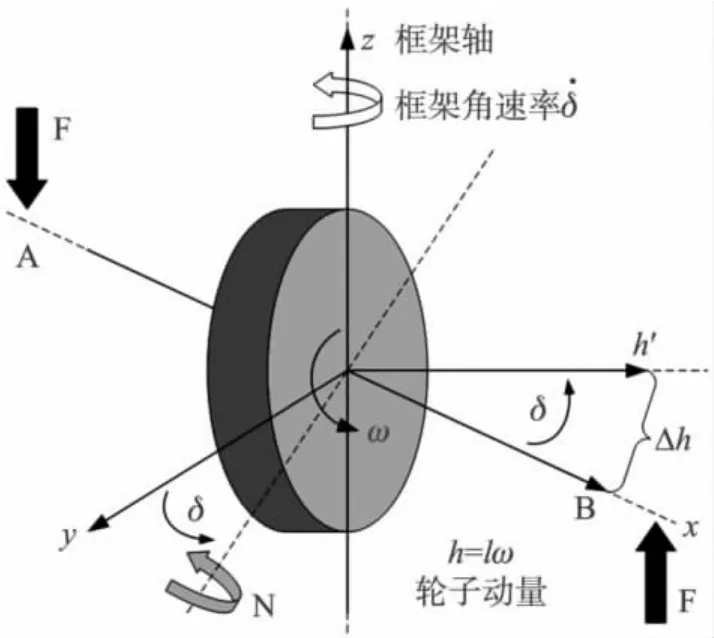
圖1 傳統控制力矩陀螺的工作原理

MCMG與傳統CMG的不同在于MCMG用振動代替了轉動。本設計所提出的MCMG結構如圖2所示。驅動轉子(圖2(c))角振動產生沿z軸的動量矩。同時，玻璃上的矩形金屬電極與SOI片上基板層(Handle Layer)之間的電容驅動整個SOI結構繞x軸轉動(圖2(d))，改變了轉子的動量方向，于是輸出沿y軸的控制力矩。

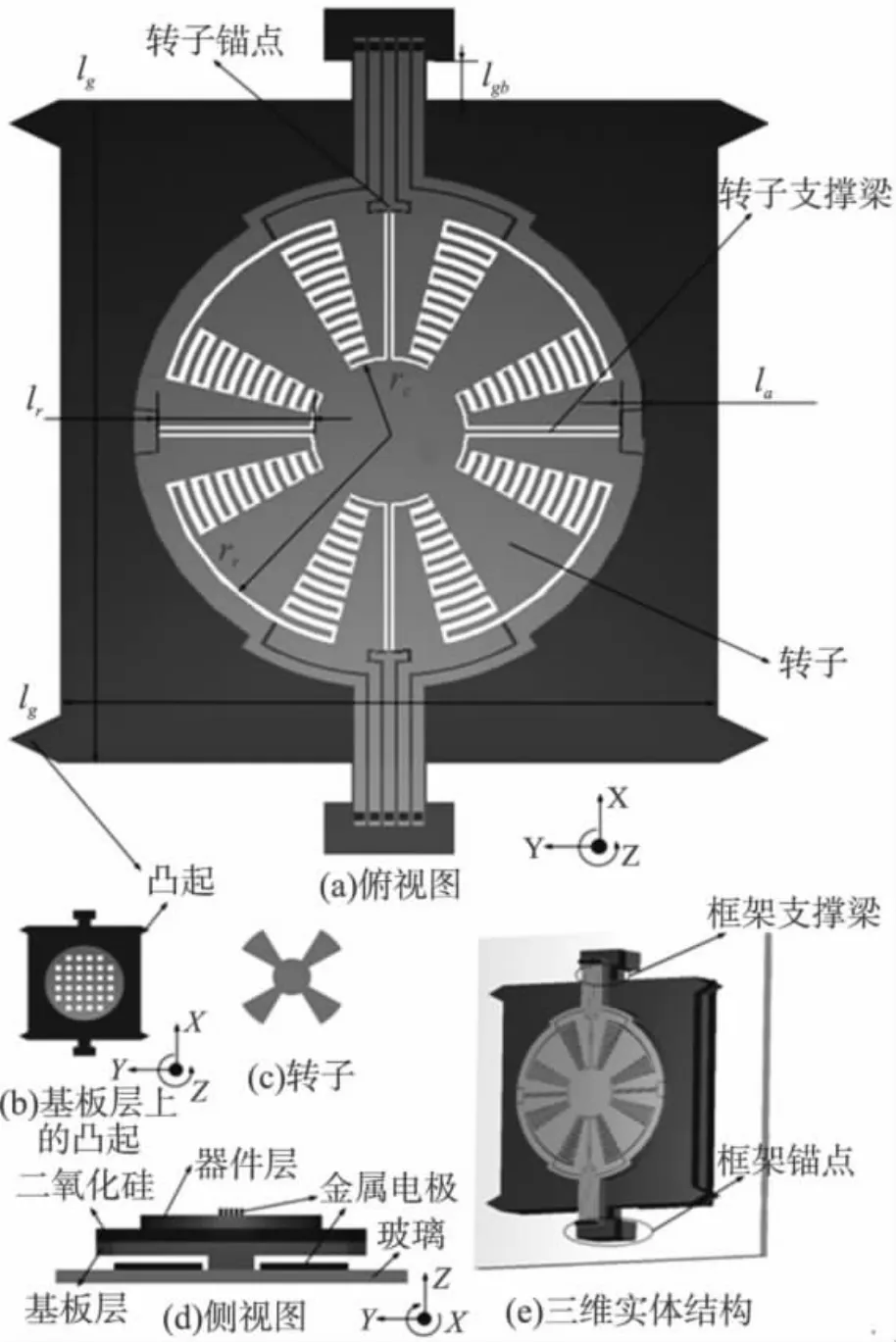
圖2 微控制力矩陀螺結構示意圖

1.1 轉子驅動

如圖3所示，微控制力矩陀螺的轉子采用弧形梳齒進行驅動，固定梳齒和與轉子固連的活動梳齒之間的電位差產生靜電驅動力矩。當V2=0(或V1=0)，活動梳齒接地時，屬于單邊驅動，轉子受到的驅動力矩為［10］

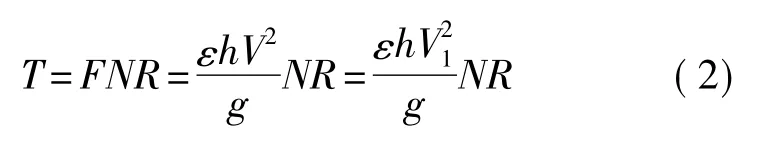
式中，F表示單個活動梳齒受到的靜電力，N為梳齒個數，R為梳齒平均半徑，ε表示介電常數，h表示梳齒高度，V表示活動梳齒與固定梳齒的電壓差，g表示梳齒間距。可見，驅動力矩雖與位移無關，但與電壓的平方成正比，即呈非線性關系。

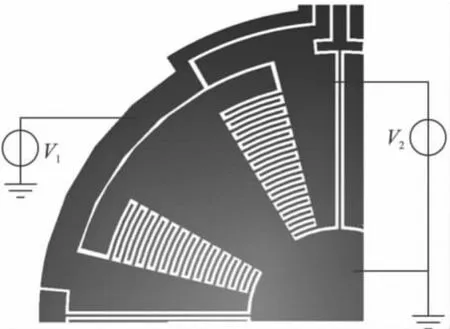
圖3 采用弧形梳齒驅動的轉子示意圖

為了使力矩與電壓之間成線性關系，采用雙邊驅動加電方式，即使V1=Vd+Va，V2=Vd－Va，此時轉子的驅動力矩為

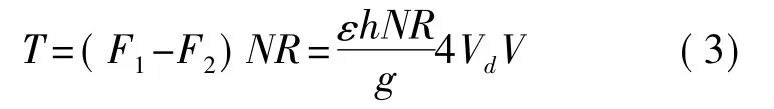
式中Vd、Va是驅動電壓的直流分量和交流分量的幅值，其余符號含義同上式，此時，力矩與電壓成線性關系，正弦變化的交流分量產生正弦變化的力矩。

轉子的動力學方程為

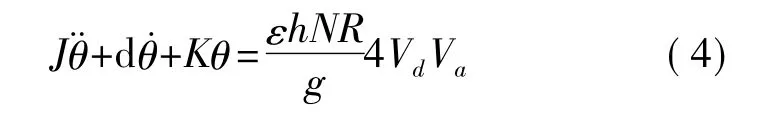
式中J表示轉子轉動慣量，d表示阻尼系數，K表示轉子的轉動剛度，θ表示轉角，其余符號含義同前。

1.2 框架驅動

如圖4所示，MCMG的框架采用平行板電極進行驅動，下電極和框架之間的電位差產生靜電驅動力矩。左邊的下電極電位為V1，右邊的下電極電位為V2，框架電位為0。當V2=0(或V1=0)時，屬于單邊驅動，框架的驅動力矩為

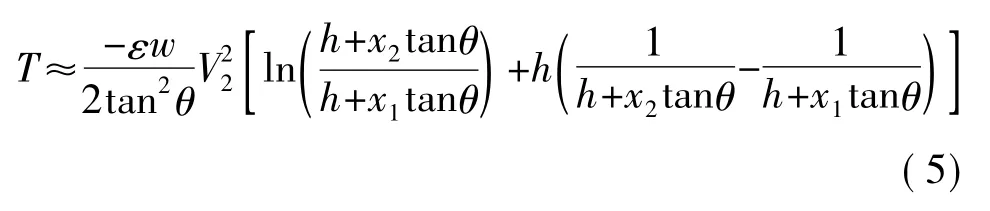
式中，T表示驅動力矩，θ表示介電常數，w表示下電極寬度，ε、h、x1、x2含義見圖 4。

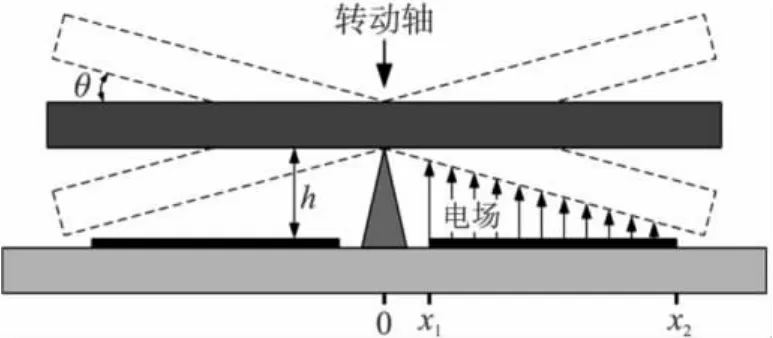
圖4 平行板扭轉驅動原理圖

在小位移時，tanθ≈θ，根據泰勒展開，忽略高次項，驅動力矩可表示成

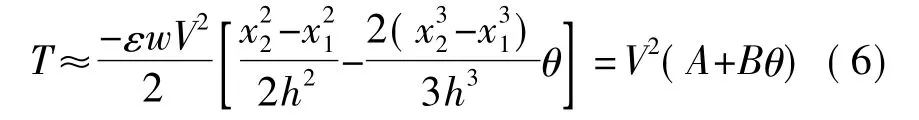
式中A和B是標記符號，其它符號含義同前。可見，驅動力矩不僅與電壓的平方成正比，呈現非線性關系，而且與位移有關。

膨潤土是自然界分布最為廣泛的粘土礦產資源之一，其應用范圍也日益廣泛。我國的膨潤土資源非常豐富，總儲量居世界前列。新疆發現的巴里坤膨潤土礦在質量和規模上都令人矚目，有著獨特的地質背景和較高的品位。

為了線性化驅動電壓與電壓的關系，采用類似于梳齒的雙邊驅動消除二次方的影響，得

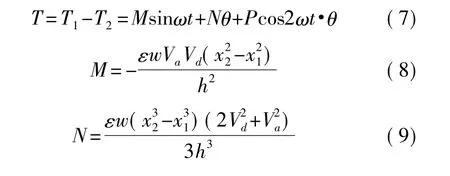
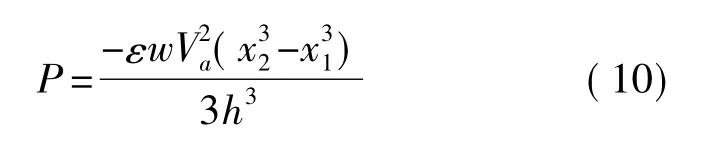
式中T是質量塊受到的總力矩，T1、T2表示左右兩個電極分別產生的力矩，Vd表示驅動電壓直流分量，Va表示驅動電壓交流分量幅值，ω是其角頻率，M、N、P是標記符號，其余符號含義同前。此時框架的動力學方程為

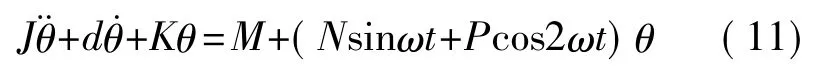
由上式及式(8)、式(9)、式(10)可得

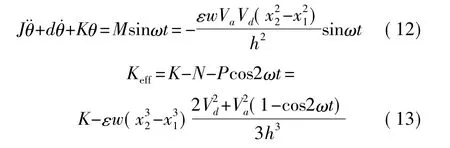
式中，J表示框架轉動慣量，d表示阻尼系數，K表示框架的轉動剛度，Keff為等效轉動剛度，其余符號含義同前。

由式(11)可看出在平行板驅動力矩中，除了包含隨電壓交流分量按正弦規律變化的分量M外，還包含與角位移成正比的時變項。前一項是希望得到的驅動力矩，后一項是不希望得到的力矩，其減小了等效轉動剛度，降低了諧振頻率，而且隨時間變化。為了減小后一項隨時間的變化，可增大直流電壓與交流電壓幅值的比例，此時Keff變化較小，正弦變化的Va產生正弦變化的驅動力矩。本設計中二者比值為2。

由于靜電驅動力矩與角位移成非線性關系，梁的回復力矩與角位移成線性關系，當角位移達到一定值時，框架會突然吸到下電極上，此現象稱為吸合。如圖5上圖所示，吸合條件為 βΘcr=0.4404，β=L/L0，Θcr=θ/Θ0。本設計采用圖5中下圖所示方案，將下電極向中間移，使β≤0.440 4，這樣就避免了吸合的發生。

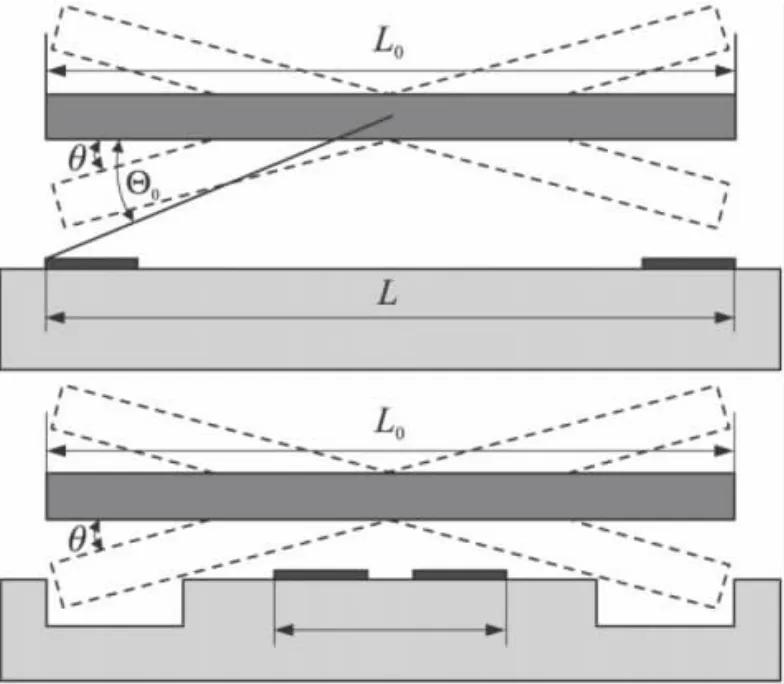
圖5 框架驅動的電極配置示意圖

1.3 設計參數及計算結果

表1為所設計的MCMG參數及取值。表中符號的含義已在前文中解釋過，下標g、r分別代表框架和轉子，a、d分別代表驅動電壓中的交流和直流部分，z代表平移模態。krz/kz，kgz/kg代表z軸平移模態和y軸旋轉模態之間的剛度比。梳齒的間隙、齒寬、齒間重疊角、總梳齒數、轉子的扇葉跨角分別為3 μm、4 μm、6°、312 個、30°，工作氣壓為100 Pa，根據以下參數可得單個MCMG的輸出力矩為1.28×10－6Nm。

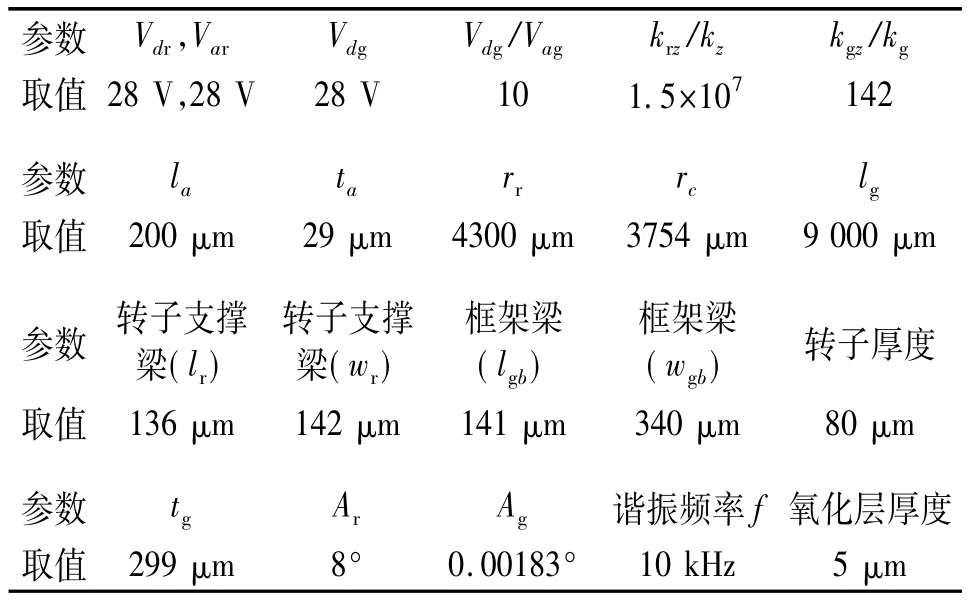
表1 微控制力矩陀螺參數

2 工藝方案

第2步，釋放二氧化硅。

第3步，在玻璃片上濺射金屬，再通過剝離(Liftoff)形成金屬電極，然后進行硅－玻璃鍵合。

第4步，在SOI硅片正面刻蝕出所需的器件結構，即第2次DRIE。

最后，劃片，打線，形成最終器件。

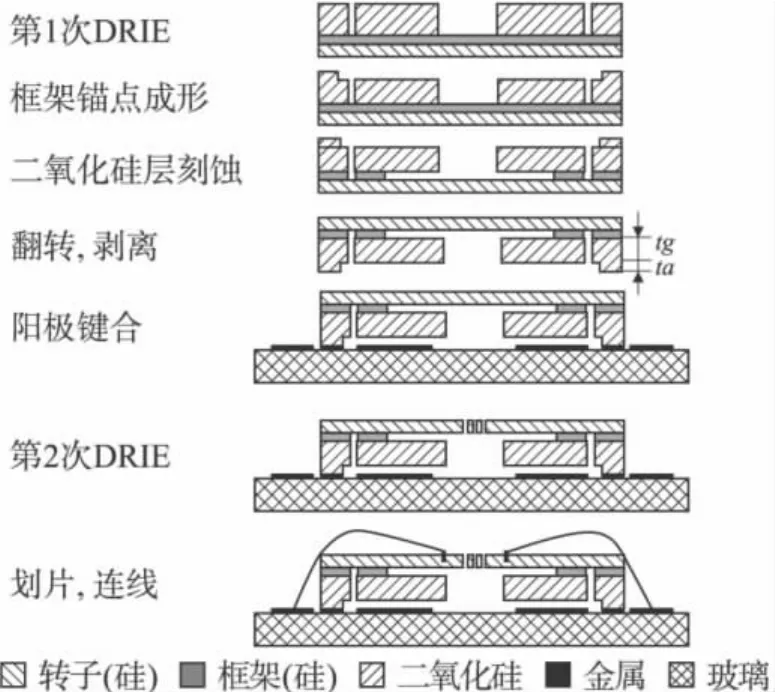
圖6 MCMG的工藝流程示意圖

3 微控制力矩陀螺的應用

單個MCMG的動量矩包括轉子振動形成的動量矩和框架振動形成的動量矩兩部分，二者方向垂直。框架的振動雖然保證了轉子動量矩方向的變化，但由于自身動量矩的變化，也輸出了一個力矩，即所謂的寄生控制力矩，其功能類似于慣性輪，需要加以消除，為此采用差動的方式。圖7中A、B兩個力矩陀螺結構完全相同，轉子和框架的驅動電壓相位相反，這樣，左右兩個陀螺有效輸出力矩方向相同，相互疊加，無效輸出力矩方向相反，相互抵消。

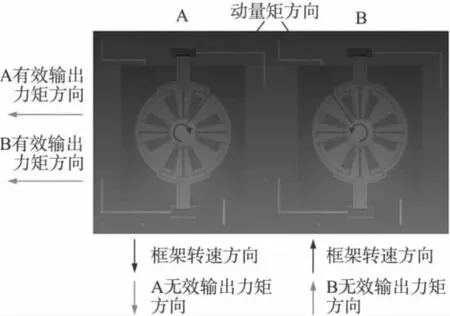
圖7 差動MCMG對消除寄生力矩示意圖

在實際方案的實施中，可通過四個MCMG所構成的陣列單元來進行，每兩個MCMG的電壓相位依次相差90°，這樣除了可消除寄生控制力矩，還能使得總體的力矩輸出得到平滑和穩定。

此外，通過設置MCMG陣列還可滿足微型衛星姿態調整的要求。假設微小型空間飛行器為邊長0.4 m，質量19.37 kg的正方體，其繞對稱軸的轉動慣量為0.57 kg·m2，單個微控制力矩陀螺的輸出力矩為1.28 μN·m 的恒定值，陀螺陣列大小為2×50×9，陀螺陣列效率為0.8，受到值為10－4Nm的嚴重干擾力矩［11］，則完成16°大范圍機動［12］需要的時間t為

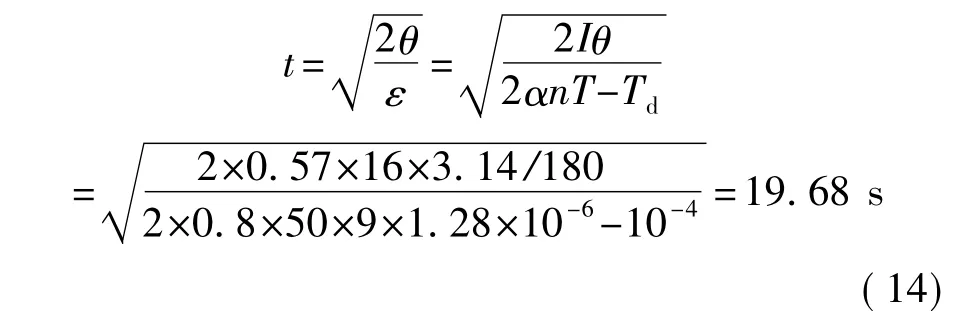
式中，θ為角度，ε為角加速度，I為轉動慣量，α為效率，n為單個陣列中的陀螺個數，T是單個陀螺的輸出力矩，Td是干擾力矩。

4 結論

與傳統的姿態控制執行機構相比，微控制力矩陀螺由于采用靜電驅動和振動方式，耗能少，幾乎沒有磨損，采用陣列配置后可使輸出力矩滿足靈敏小衛星的快速機動需求。

［1］Sanjay P Bhat，Pawan K Tiwari.Controllability of Spacecraft Attitude Using Control Moment Gyroscopes［J］.IEEE Trans.Automat.Control，2009，54(3):585－590.

［2］谷松，賈繼強，金光.快速機動小衛星執行機構研究［J］.光學精密工程，2008，16(8):1541－1541.

［3］湯亮，陳義慶.雙框架控制力矩陀螺群的建模與分析［J］.航空學報，2008，29(2):424－429.

［4］Roser X，Sghedoni M.Control Moment Gyroscopes(CMG’s)and their Application in Future Scientific Missions［C］//Proceedings of the 3rd ESA International Conference on Spacecraft Guidance，Navigation and Control Systems，Noordwijk，Netherland.1997:523－528.

［5］徐超，李兆澤，萬紅.MEMS固體微推進器中Cr薄膜點火電阻的研究［J］.傳感技術學報，2006，19(5):1411－1412.

［6］劉洪英，皮喜田，周承文.基于MEMS的消化道定點釋藥微系統研究［J］.傳感技術學報，2008，21(3):381－384.

［7］Reiter J，Bohringer K，Campbell M.MEMS Control Moment Gyroscope Design and Wafer-Based Spacecraft Chassis Study［C］//Proc.SPIE，1999:122－128.

［8］Bedrossian Nazareth S，Bhat Sagar，Kang We，et al.Zero-Propellant Maneuver Guidance［J］.IEEE Control Systems Magazine，2009，29(5):53－73.

［9］Bhatia V B.Classical Mechanics:With Introduction to Nonlinear Oscillations and Chaos［M］.Narosa Publishing House，1997:273－282.

［10］Yeh J A，Chen C，Lui Y.Large Rotation Actuated by in-Plane Rotary Comb-Drives with Serpentine Spring Suspension［J］.Journal of Micromechanics and Microengineering，2005(15):201－206.

［11］Robert Osiander，M Ann Garrison Darrin，John L Champion.MEMS and Microstructures in Aerospace Applications［M］.CRC Press，2005:2－5.

［12］Jaime Esper.Modular Adaptive Reconfigurable Systems［C］//AIP Conf.Proc，2005，746:1033－1043.