關于互易二端口網絡互連的討論

田社平，陳洪亮，張 峰

(上海交通大學電子信息學院，上海200240)

互易電路是一類較為特殊的電路，它是電路課程教學中較為重要的教學內容之一。互易二端口電路是互易電路的典型形式，其性質可由互易定理加以描述。二端口電路的互連亦是電路課程教學的重要內容。如果將互易二端口電路互連，互連后得到的二端口電路是否仍然滿足互易性?如果要滿足互易性則需設定什么條件?互易二端口電路的互連有何應用?這些都是筆者在教學過程中碰到的問題。

1 互易二端口電路的判定規則

二端口電路的參數矩陣元素間的關系可以用來判定一個二端口電路是否為互易二端口電路。如果已知二端口電路的開路電阻矩陣R，或電路電導矩陣G，或混合參數矩陣H和，或傳輸參數矩陣A和，則當二端口參數矩陣元素滿足如下關系時，該二端口電路為互易二端口電路［1]:

2 互易二端口電路互連的互易性

常見的二端口互連形式包括串聯、并聯、串-并聯、并-聯和級聯等。如果互連的二端口電路是互易的，則在各種互連形式下得到的總二端口電路的互易性具有下述結論:對互易二端口電路N1和N2，如果互連(串聯、并聯串－并聯、并－串聯和級聯)后N1和N2仍然滿足端口定義，則互連得到的總二端口電路也是互易的。以下分別予以證明。

(1)串聯和并聯

假設N1和N2的r參數矩陣分別為

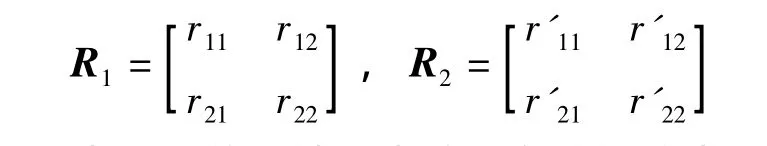
串聯后總二端口電路r參數矩陣為R。由于串聯后N1和N2仍然滿足端口定義，因此有［2]

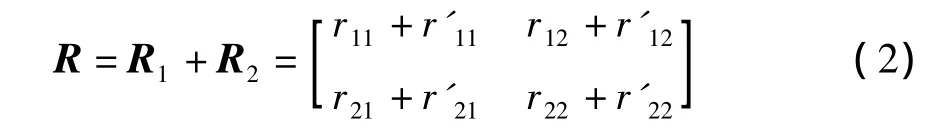
因N1和N2是互易的，由式(1)可得r21=r12，r'21=r'12，因此有

即R為對稱矩陣，因此串聯后總二端口電路是互易的。

同理，可證互易二端口電路N1和N2并聯后總二端口電路也是互易的。

(2)串－并聯和并－串聯

假設N1和N2的h參數矩陣分別為

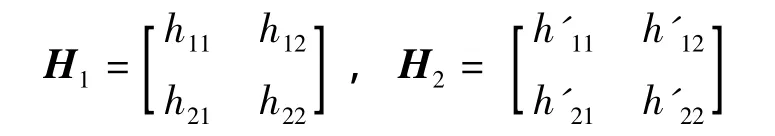
串－并聯后總二端口電路h參數矩陣為H。由于串－并聯后的N1和N2仍然滿足端口定義，因此有［2]

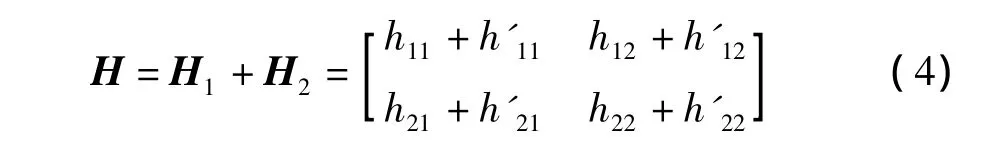
因N1和N2是互易的，由式(1)可得，h21=-h12，h'21=-h'12，因此有

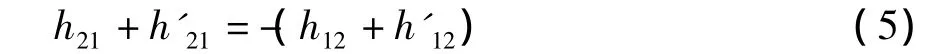
即H為對稱矩陣，因此，串－并聯后總二端口電路是互易的。

同理，可證互易二端口電路N1和N2并－串聯后總二端口電路也是互易的。

(3)級聯電路。

假設N1和N2的a參數矩陣分別為

級聯后總二端口電路a參數矩陣為A。由于級聯后N1和N2總是滿足端口定義，因此有［2]

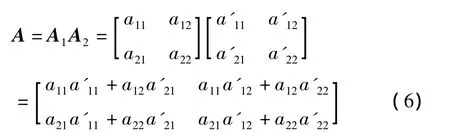
從而得到

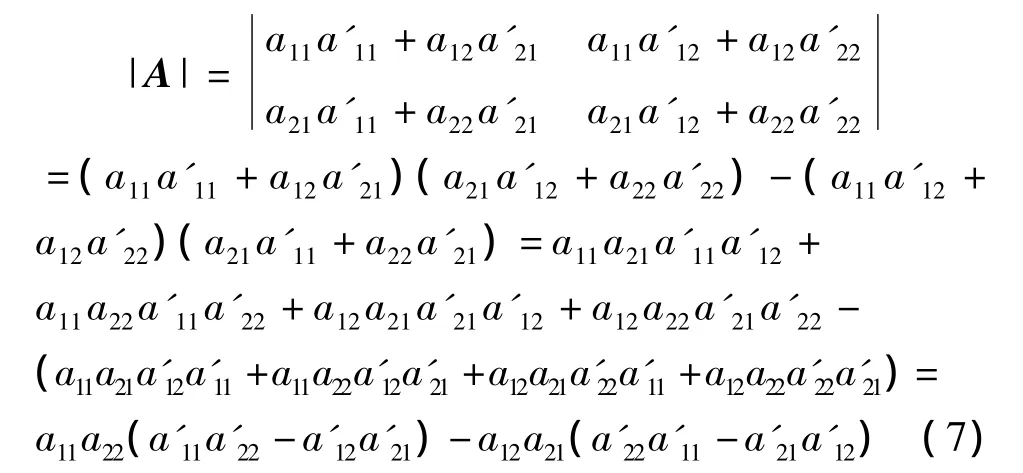
因N1和N2是互易的，由式(1)可得a11a22－a12a21=1，a'11a'22－a'12a'21=1，由該兩式及式(7)可得由式(1)可知，級聯后總二端口電路是互易的。由上述證明過程可知，對多個互易二端口電路的互連，上述結論仍然成立。

［例1]試判斷圖1所示電路是否為互易二端口電路。

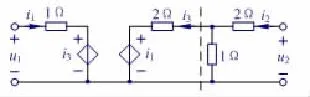
圖1 級聯二端口電路

解:將圖1電路看作兩個二端口電路(從虛線處斷開)的級聯，由于虛線右邊電路僅由電阻構成，因此該二端口電路為互易電路。虛線左邊二端口電路的r參數矩陣滿足互易條件，因此圖1電路為互易的。

我們也可通過求出圖1電路的參數矩陣進行判斷，但過程會復雜一些。

3 互易二端口電路互連的有效性判斷

二端口電路在串聯、并聯和串－并聯和并－串聯時存在有效連接(二端口電路互連后仍滿足端口定義)的問題［3]。如果要求互易二端口互連后總二端口電路仍然是互易的，則須保證互連是有效連接。如果互連不是有效連接，則可采用變壓器隔離法來實現有效連接，圖2給出了并聯二端口電路的變壓器隔離方法。

值得指出的是，變壓器可連接在二端口電路N1和N2的輸入、輸出端口的任一端口。對串聯和串－并聯和并－串聯二端口電路的變壓器隔離方法，可給出類似結果。

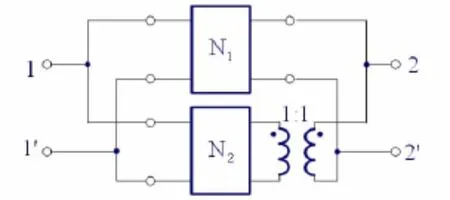
圖2 并聯二端口電路的變壓器隔離

4 對稱二端口電路的互連

如果互易二端口電路的兩個端口可以交換而端口的電壓和電流的數值不變，則稱該二端口電路是對稱的。對稱二端口電路的參數矩陣的元素除滿足式(1)之外，還滿足如下關系:

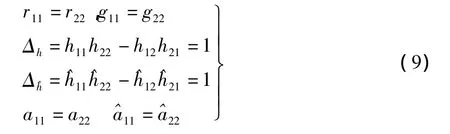
采取類似的推導方法，我們可以得到如下結論:對兩個對稱二端口電路N1和N2，如果互連(串聯、并聯和串－并聯、并－串聯、級聯)后N1和N2仍然滿足端口定義，則互連得到的總二端口電路也是對稱的。

5 結語

本文針對互易二端口電路互連的互易性進行了討論，并給出了一般性結論。盡管電路的互易性不具有普遍性，互易電路的性質(互易定理)的應用面也較窄，但筆者認為，通過對電路包括二端口電路互連的互易性進行深入討論，有助于加深學生對互易電路及二端口電路互連等概念的理解。本文的討論拓寬了電路教材中關于互易電路及二端口電路互連的教學內容，有助于電路課程的教學，可供從事電路教學的教師參考。

［1] 李瀚蓀.簡明電路分析基礎［M] .北京:高等教育出版社.2002

［2] 陳洪亮，張峰，田社平.電路基礎［M] .北京:高等教育出版社.2007

［3] 田社平，張峰，陳洪亮.雙口網絡有效互連的判據和實現［J] .南京:電氣電子教學學報，2005(5)