一種非線性PID控制器建模與仿真

厲兆慧，夏 洪

（東華理工大學 機械與電子工程學院，江西 撫州 344000）

由于PID控制器的簡單、有效以及不依賴于被控對象數學模型的特點，PID控制技術在控制實踐中的應用越來越廣泛。但是，傳統線性PID控制中，比例、積分和微分環節之間為線性組合，容易造成系統靜態與動態性能、跟蹤設定值與抑制擾動之間的矛盾。因此，有必要利用非線性特性來改造傳統的PID控制器，以獲得更高的控制性能。

本文通過分析PID各系數隨系統誤差信號的變化關系，分別給出了比例、積分和微分增益系數關于誤差信號的連續非線性函數。然后，用這3個函數代替傳統PID控制器的3個增益系數，從而獲得非線性PID控制器的可用模型。

通過對二階系統的數據仿真可以得出，非線性PID控制器可以改善傳統PID控制器在快速性和穩定性方面的缺陷，并且所設計的非線性PID控制器能大大降低系統階躍響應的上升時間，同時也證明了這類非線性PID控制器的有效性。

1 傳統的PID控制器

PID控制器具有簡單的控制結構，在實際應用中又較易于整定，因此它在工業過程控制中有著最廣泛的應用，大多數PID控制器是現場調節的，現在有很多不同類型的調節率，利用這些調節率，可以對PID控制器進行精確而細致的現場調節。

PID控制器的數學模型

其中，Kp為比例系數，Ti為積分時間常數，Td為微分時間常數，Ki為積分系數，Kd為微分系數，其中。

因此，PID控制器的設計就是確定PID控制器的3個參數，采用Ziegler-Nichols整定法則，通過實驗方法確定臨界增益和相應的周期，則PID控制器的參數計算公式為

對于簡單的PID控制器，上述參數一經整定，在整個過程中便要一直保持不變。這樣的控制器很難同時滿足跟蹤設定值和抑制擾動的要求，也無法適應過程特性的變化，而且傳統PID控制器中的線性組合常引起系統快速性與超調量之間的矛盾。

2 非線性PID控制器

要建立非線性PID控制器模型，最常用的方法是通過調整傳統PID控制器的系數Kp，Kd和來建立模型，而修改PID控制器系數最主要的方法還是根據系統輸出誤差e的大小來生成函數Kp(e(t))，Ki(e(t))和 Kd(e(t))，然后以這三個非線性函數來代替傳統PID控制器的系數。下面，可以通過分析系統的階躍響應曲線(見圖1)來構建非線性PID控制器的各環節的增益系數，從而獲得非線性PID控制器的可用模型。

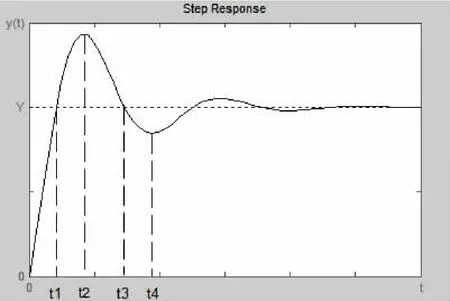
圖1 一般系統的階躍響應曲線

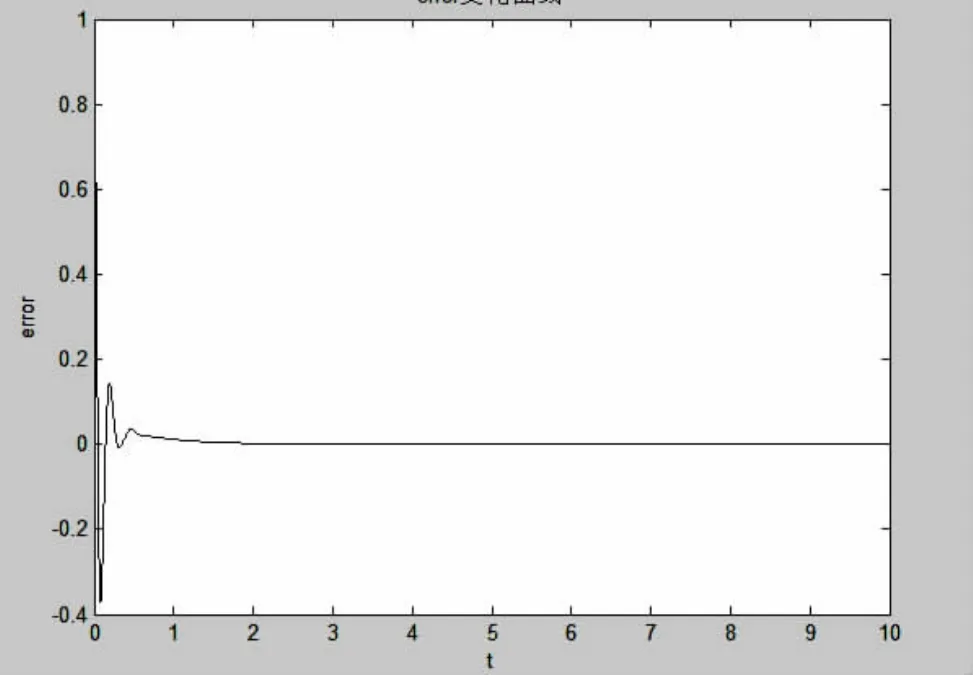
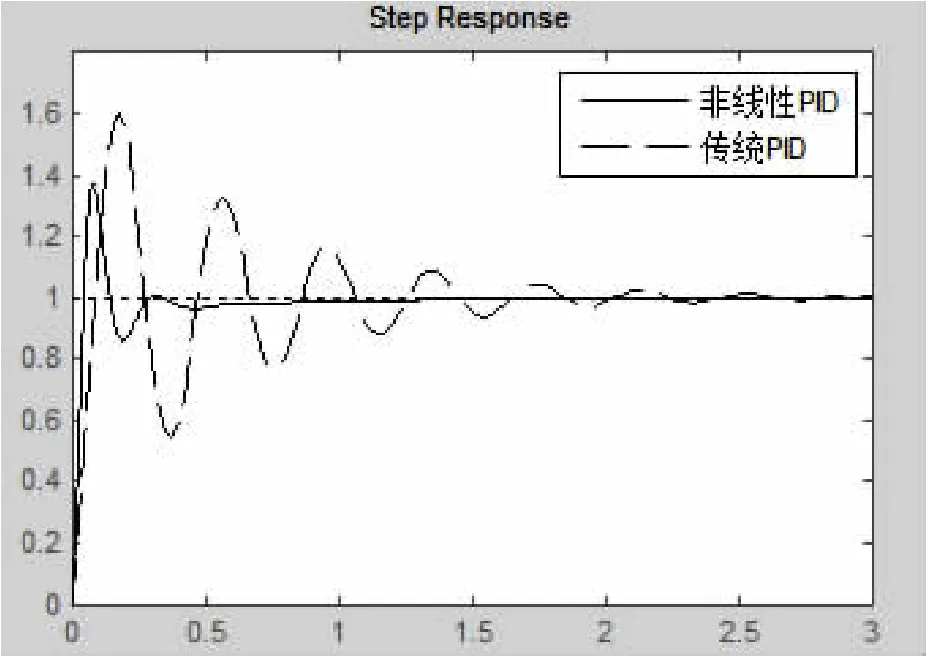
（1）比例系數Kp。比例系數的作用是能夠提高系統響應速度,減小超調。想要達到既快速又穩定調節的目的，就必須在遠離穩定值時，比例系數的絕對值應該大，而在穩定值附近時，比例系數的絕對值又應該很小。所以，在響應時間段0≤t≤t1，在初始時應該比較大，為了減小超調量，希望Kp隨著誤差e的減小而減小，在時間段t1

式中:ap，bp，cp為正實常數。 當 e→±∞ 時，取最大值 ap+bp，當e=0時，Kp取最小值ap，cp控制Kp的變化速率。

（2）積分系數Ki。積分環節的作用是消除系統的靜態誤差，如果積分系數過大會使系統的過渡過程變長。所以，當誤差信號較大時，希望Ki較小，以防止系統產生震蕩，有利于減小超調量；而當誤差較小時，希望Ki增大，以盡快消除系統的靜態誤差。即Ki絕對值與e(t)絕對值變化方向相反。由此，可以得出積分系數Ki可表示為：Kie(t))=aisech(bie(t))

式中:ai，bi為正實常數； 當 e→±∞ 時，Ki取最小值 0，當e=0時，取最大值ap；bi的決定了Ki的變化速度。

（3）微分系數Kd。微分環節可以抑制超調量，增加系統阻尼，能起到提前校正系統的作用，但是會使系統的響應速度變慢。在0≤t≤t1時間段，Kd應逐漸由小變大，這樣就可以在不影響系統響應速度的前提下，抑制超調的產生；在t1

式中:ad，bd，cd，dd為正實常數； 當 e→-∞ 時，Ki取最大值ad+bd，當 e→+∞ 時，取最小值 ad，當 e=0 時，Ki取值為 ad+bd/（1+cd）；dd決定了積分系數 Kd的變化速率。

由以上分析可知，如果非線性函數中的各項參數選擇合適的話，能夠使控制系統達到響應速度快，并無超調量的目的。由于非線性PID控制器中的各項增益系數能夠隨誤差e的變化而變化，因此其魯棒性也比傳統的PID控制器強。

（4）非線性PID控制模型。在得出上面各模塊的非線性函數Kp(e(t))，Ki(e(t))，Kd(e(t))之后,也就同時得出了非線性PID控制器的模型,即u(t)=[ap+bp(1-sech(cpe(t)))]e(t)+[aisech(bie(t))]

式中：ap，bp，cp，ai，bi，ad，bd，cd，dd均為正實常數。

3 仿真研究

為了驗證非線性PID控制器的有效性，利用MATLAB分別對傳統PID和非線性PID的單位階躍響應進行了數值仿真，被控對象為典型的二階系統，其傳遞函數為：

采用傳統的Ziegler-Nichols規則整定固定增益的傳統PID控制系數為:Ti=0.1，Td=0.025。

非線性PID控制器模型中的信號誤差e隨時間變化曲線如圖2所示，非線性增益系數Kp，Ki，Kd隨誤差信號e的變化曲線如圖3所示:

圖2 誤差e隨時間變化曲線

圖3 非線性系數隨誤差變化曲線

從圖 3可以看出 Kp，Ki，Kd的變化規律符合 PID控制原理，所以具有很好的仿真效果。在上述系數條件下，傳統PID控制器與非線性PID控制器的單位階躍響應如圖4所示。

圖4 非線性PID與傳統PID單位階躍響應比較圖

由圖4可見，非線性PID控制器的階躍響應速度明顯優于傳統固定增益系數的PID控制器的響應速度，非線性PID控制可以使系統快速穩定地收斂到給定的誤差范圍內，而傳統的PID控制不能穩定地收斂，系統存在大幅度的振蕩。可見，非線性PID控制比傳統的PID控制有更大的優越性和廣泛的適應性，可以應用于非線性系統中。

4 結語

本文利用一種非線性函數對傳統PID控制器進行改造的方法，通過分析傳統PID控制系數隨系統誤差e變化的關系，分別給出了比例、積分和微分增益系數關于誤差信號的二次非線性函數，得到了比較靈活的增益策略，大大簡化了3個增益系數的非線性函數模型。通過對二階系統的階躍響應仿真可以看出，所提出的非線性PID控制器比傳統固定增益的PID控制器具有更好的動靜態性能，并且對于某些被控對象具有比傳統PID更好的調節性能及更大的穩定域。上述算法簡單容易且實現，因此具有較高的實際應用價值。但是，如果從理論上分析其具體的適用范圍、參數整定規則等，有待于進一步的深入研究。

[1]郭彥青，姚竹亭，王楠.非線性PID控制器研究[J].中北大學學報，2006，27(5),423-425.

[2]蘇玉鑫，段寶巖.一種新型非線性PID 控制器[J].控制與決策，2003，18(1):126-128.

[3]Wang Q G，Lee T H，Fung H W.PID tuning for improved perfor mance[J].IEEE Transactions on Control Systems Technology，1999，7(4):457-465.

[4]劉金琨.先進PID 控制及其MATLAB仿真[M].北京：電子工業出版社，2002，11.