基于多尺度小波模極大融合的寬帶頻譜感知算法
王桂良,路友榮,韓 猛,徐 剛
(西南電子電信技術研究所,成都610041)
1 引 言
頻譜感知中能量檢測、匹配濾波、循環平穩特性檢測等技術主要針對窄帶信號[1]。對于寬帶頻譜感知,可利用中心頻點可調的窄帶濾波器通過多次窄帶頻譜感知來實現[2];另一種更為直接的結構是Z.Quan提出的利用多個窄帶濾波器組成濾波器組實現寬帶頻譜感知[3]。但上述方案分別會帶來時間上的巨大開銷以及設備復雜度的增加。
Z.Tian等人提出了一種基于小波分析的寬帶頻譜感知算法[4],他們利用小波邊緣檢測識別信號功率譜的奇異點,從而實現寬帶信號檢測,但他們的信號模型較為理想,對實際信號的適用性不高[5]。Almeida改進了Z.Tian的算法,提出了一種綜合不同尺度下連續小波變換結果的檢測手段,但沒給出信號模型及尺度因子的選擇方法,影響其算法實用性[6]。S.Chantaraskul等人在2009年設計了一套試驗系統,驗證了小波分析在寬帶頻譜監測中的有效性[7]。此外,李曉艷等人提出利用噪聲和信號奇異點具有不同Lipschitz指數的特點實現噪聲去除[8],該算法對噪聲奇異點的去除十分有效,但對于信號帶內起伏帶來的奇異性效果不明顯,虛警率較高。
本文在綜合各種實際因素建立信號模型的基礎上,提出了多尺度小波模極大融合算法,同時考慮帶寬與Lipschitz指數對信號功率譜小波變換模極大在不同尺度下傳播特性的影響,對不同帶寬的信號采取不同尺度的小波模極大進行分選,最后將分選結果融合形成檢測結果。實際信號測試表明,該算法能夠解決傳統手段對寬帶和窄帶信號無法兼顧的問題,并且能夠對由于存在同步、導頻等特殊序列而導致功率譜形狀不規則的信號實現有效檢測。
2 信號模型
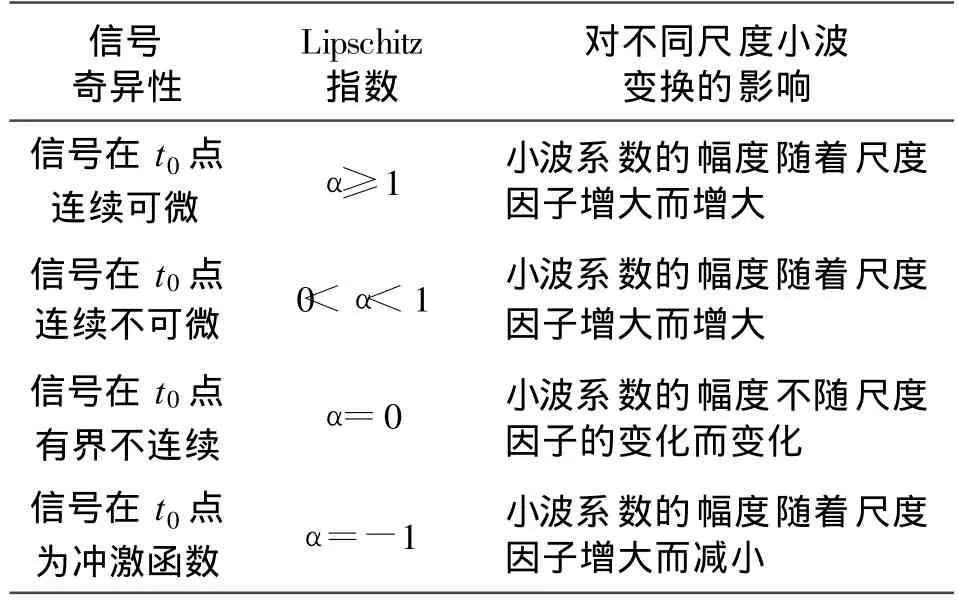
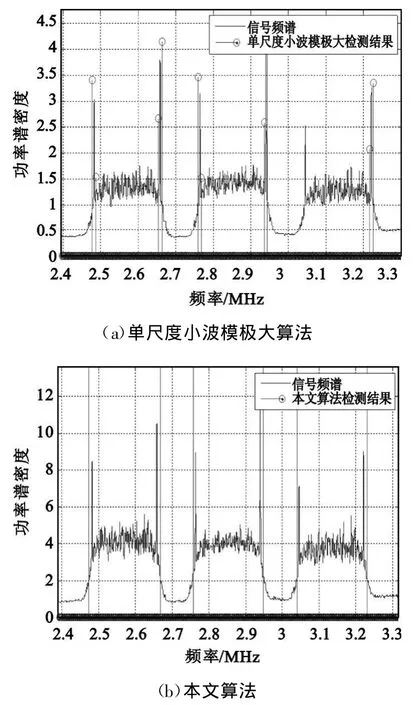
考慮帶寬為B的頻帶范圍[fa,fb],在該頻段內存在N個信號。設它們的頻率邊界位于 fa 由于理想低通濾波器無法實現,實際中人們往往使用升余弦濾波器對基帶信號進行脈沖成形,這導致信號功率譜邊緣是連續可微的。此外,成形濾波器帶內起伏、信道頻率選擇性衰落等原因還會造成信號存在帶內起伏。這些信號特征會給頻譜感知帶來負面影響:頻譜邊緣的光滑變化會導致小尺度下小波變換的系數較小,容易造成漏檢;信號的通帶起伏則會造成虛警、誤判。為充分考慮各種實際因素給寬帶頻譜感知帶來的影響,對信號模型作如下設定: (1)頻帶范圍[fa,fb]已知,信號數目 N以及它們各自的頻段Bn頻段未知,且這些參量在一次檢測中保持不變; (2)背景噪聲為加性高斯白噪聲,均值為零,雙邊功率譜密度為Sw(f)=N0/2, f。 (3)信號存在帶內起伏,且邊緣連續可微; (4)不同信號帶寬差異較大,用Bmin表示信號的最小帶寬,Bmax表示信號的最大帶寬,兩者比值在極端情況下滿足 頻譜感知需要解決的問題是如何準確估計[fa,fb]內信號個數N、每個信號的頻段范圍Bn及其載頻、信噪比等參數。在上述信號模型基礎上,頻譜感知可歸結為邊緣檢測問題,進而利用小波分析求解。 若平滑函數θ(x)可微,用ψ1(x)表示θ(x)的一階微分: 由平滑函數以及小波母函數定義可知ψ1(x)可作為小波母函數。信號 f(x)使用ψ1(x)為小波母函數在尺度s下的小波變換定義為 可證明 小波系數能夠反映信號的局部奇異性;同樣,不同類型的奇異性會對小波系數在不同尺度下的傳播造成不同影響,數學上往往采用Lipschitz指數來描述函數的奇異性。 定義1(一致 Lipschitz α) 設0≤α≤1,稱函數 f(x)在區間(a,b)為一致Lipschitz α的,當且僅當存在常數K使得對于任意(x0,x1)∈(a,b)有 信號的Lipschitz指數同小波變換結果沿不同尺度的傳播特性由如下定理給出。 定理1:設0<α<1,若函數 f(x)在區間(a,b)是一致Lipschitz α的,則存在常數K使得對于任意x∈(a,b),f(x)的二進小波變換結果滿足 由式(5)可以歸納信號奇異性對小波系數在不同尺度下傳播特性的影響,如表1表示。 表1 信號奇異性與Lipschitz指數的關系及其對不同尺度小波系數的影響Table 1 The relationship between singularities and Lipschitz exponent 依據文獻[4]模型,信號功率譜S(f)邊緣有界不連續,信號頻帶邊緣處Lipschitz指數 α=0,S(f)中信號邊緣處小波變換幅度不隨尺度因子變化。在文獻[4]模型基礎上單尺度小波模極大以及多尺度小波乘積都能取得較好的檢測效果。由本文信號模型可知實際信號功率譜 Sr(f)邊緣連續可微,Lipschitz指數α>0,小波變換的幅度隨尺度因子增大而增大。為取得更好的檢測效果,應用大尺度下的小波系數進行邊緣檢測。由模型條件5可知若平滑函數的尺度過大,會使得帶寬較小的信號被平滑掉,無法形成模極大而造成漏檢。同時考慮信號模型條件4、5情況下,合理的思路是對不同帶寬的信號采用不同尺度的小波變換結果進行檢測,基于此本文提出了多尺度小波模極大融合算法。 算法流程如圖1所示。 圖1 算法流程Fig.1 The algorithm′s whole process (1)功率譜估計 根據采樣頻率fs,頻率分辨率要求Δf等指標估計信號功率譜Sr(f)。 (2)功率譜離散二進小波變換 對Sr(f)進行離散二進小波變換,本文采用二次樣條函數近似高斯函數的一階微分作為小波母函數,對 Sr(f)進行離散二進小波變換采用M.Holschneider及 R.Kronland-Martinet等人提出的 à trous算法,如圖2所示。 圖2 快速二進小波變換的à trous算法Fig.2 Algorithm à trous for fast dyadic wavelet transform (3)劃分信號帶寬,確定相應小波變換階數 由于不同信號的帶寬跨度范圍事先未知,為保證不發生漏檢應當對的帶寬范圍進行全覆蓋劃分。以信號功率譜Sr(f)的長度 N=216為例,可按數量級對信號帶寬進行如圖3形式劃分,圖中數字為信號在功率譜中所占點數,換算為實際帶寬如表2所示。表2同時給出了檢測不同帶寬信號推薦使用的小波變換階數及相應小波濾波器gj的長度。 圖3 按數量級對信號帶寬進行劃分Fig.3 Compart signals into different subsets based on their bandwidth 表2 不同規格信號所對應的實際帶寬、小波變換階數及小波濾波器長度Table 2 The bandwidth,wavelet transform order and wavelet filter′s length of different types of signals (4)利用不同階數小波變換的模極大結果進行多尺度信號檢測 由信號模型條件4可知寬帶信號往往存在劇烈的帶內起伏,這種起伏在小尺度下易被誤判為窄帶信號,因此首先從大信號開始進行信號檢測,一旦判定為大信號將不再對該頻譜范圍進行小尺度下的信號檢測,從而避免出現寬帶信號的帶內起伏被誤判為窄帶信號的現象,整個流程如圖4所示。 圖4 多尺度信號檢測流程Fig.4 Multi-scale signal detection process (5)根據檢測結果,估計信號參數 完成信號檢測以后,可以根據檢測結果估計信號載頻fc、帶寬B以及信噪比(SNR)等參數。設第i個信號起始頻率f2i-1,結束頻率f2i,則信號帶寬Bi=f2i-f2i-1,載頻確定了各個信號的位置,同時也確定了“頻譜空穴”的位置,可據此估計噪聲功率 N0,進而采用文獻[4]的方法估計各個信號的信噪比。 下面通過實際信號的實驗驗證來證明該算法的有效性。 實際信號采樣率fs=93.3 MHz,要求頻譜分辨率Δf≤1 kHz,采用周期圖法用217點FFT運算估計其信號功率譜Sr(f),對Sr(f)采用本文算法進行檢測的結果如圖5所示。 圖5 本文算法的檢測結果Fig.5 Dectection result of the proposed algorithm 圖5中兩條相鄰直線確定了信號的起始和結束頻點,其幅度為對應位置處Sr(f)的小波變換系數。圖5(a)中可分辨的信號共有72個,應用本文算法可全部準確檢測。對于圖5(a)中5MHz存在的密集窄帶信號,檢測結果展開如圖5(b)所示,由圖可知對帶寬非常窄的信號該算法依舊具有良好的檢測性能。 圖6為存在同步序列的信號檢測結果,圖6(a)采用文獻[4]中方法,其算法將同步信息造成的尖峰誤判為窄帶信號;圖6(b)為本文算法的檢測結果,通過多分辨率分析的手段,將該信號識別為寬帶信號,有效解決了上述問題。 圖6 本文算法和傳統算法對存在同步信息的信號檢測性能對比Fig.6 Comparison of the proposed algorithm and traditional algorithm for signalswith synchronization information 圖7 3種算法性能對比Fig.7 Performance comparison among three algorithms 圖7給出了14組實際信號本文算法和兩種傳統算法的性能比較,可以看出本文算法有著更高的檢測率和更低的誤判率,且不會因信號惡化(如出現大量密集窄帶信號或者特殊譜形狀的信號)而導致檢測性能下降。 綜上所述,本文算法存在如下幾方面的優勢: (1)信號模型更加真實,考慮了成形濾波、帶內起伏以及信道不理想造成的不良影響; (2)對一些頻譜形狀特殊的信號(如存在導頻、同步信息的TDMA信號)具有良好檢測性能; (3)能夠兼顧寬帶和窄帶信號,檢測結果不受信號帶寬影響。 為滿足寬帶頻譜感知對檢測精度、檢測時間、設備復雜度等要求,本文分析了導致傳統頻譜感知算法性能下降的原因,將成形濾波器的平滑效應,通帶起伏、信道非理想等因素加入到信號模型中來,結合小波多分辨率分析思想,提出了一種多尺度小波模極大融合算法。對不同帶寬的信號采用不同尺度的小波變換進行檢測,并將不同尺度下的檢測結果融合得到最終結果。實際信號測試結果表明,這一算法能夠解決傳統手段對寬帶和窄帶信號無法兼顧的問題,且能對一些特殊頻譜形狀的信號進行檢測,檢測性能相對傳統算法有明顯提高。 [1]Haykin S.Cognitive Radio:Brain-Empowered Wireless Communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220. [2]Yucek T,Arslan H.A survey of spectrum sensing algorithms for cognitive radio applications[J].IEEE Communications Surveys&Tutorials,2009,11(1):116-130. [3]Quan Z,Cui S,Sayed A H,et al.Wideband spectrum sensing in cognitive radio networks[C]//Proceedings of 2008 IEEE International Conference on Communications.Beijing:IEEE,2008:901-906. [4]Zhi T,Giannakis G B.Compressed Sensing for Wideband Cognitive Radios[C]//Proceedings of 2007 IEEE International Conference on Acoustics,Speech and Signal Processing.Honolulu,HI:IEEE,2007:1357-1360. [5]Arslan H.Cognitive Radio,Software Defined Radio,and Adaptive Wireless Systems[M].New York:Springer,2007. [6]Almeida E,Carvalho P,Cordeiro P,et al.Experimental Study of a Wavelet-based Spectrum Sensing Technique[C]//Proceedings of the 42nd Asilomar Conference on Signals,Systems and Computers.Pacific Grove,CA:IEEE,2008:1552-1556. [7]Chantaraskul S,Moessner K.Implementation of Wavelet Analysis for Spectrum Opportunity Detection[C]//Proceedings of 2009 IEEE International Symposium on Personal,Indoor and Mobile Radio Communications.Tokyo:IEEE,2009:2310-2314. [8]李曉艷,張海林,胡飛.應用小波變換的認知無線電頻譜檢測[J].計算機工程與應用,2011,47(13):4-7.LI Xiao-yan,ZHANG Hai-lin,HU Fei.Spectrum sensing based onwavelet transformfor cognitive radio[J].Computer Engineering andApplications,2011,47(13):4-7.(in Chinese)3 多尺度小波模極大融合算法
3.1 小波邊緣檢測的理論基礎

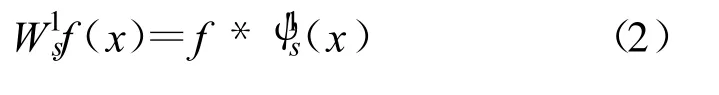
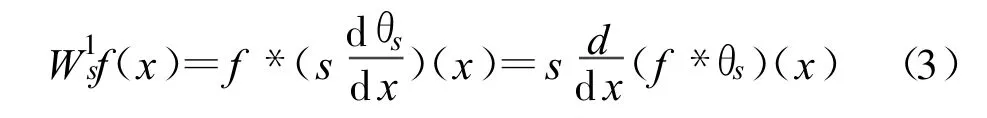
3.2 信號模型對小波系數在不同尺度下傳播特性的影響


3.3 算法步驟





4 測試驗證
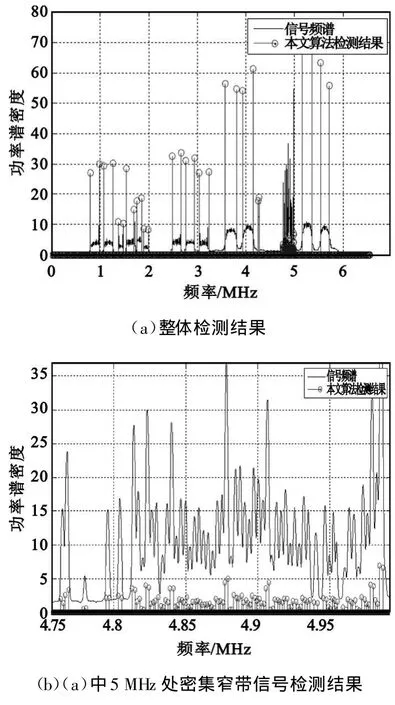

5 結 論

