基于分數(shù)階傅里葉變換的脈內信號調制方式識別

寧 輝,陳 超

(1.北京航空工程技術研究中心特設研究室,北京100076;2.空軍航空大學航空電子工程系,長春130022)

1 引 言

目前,大帶寬和復雜波形的雷達信號在軍事領域中得到了廣泛應用,常規(guī)的雷達脈沖描述字已很難準確描述這種雷達信號的特征。為了更加有效地檢測雷達信號,對雷達進行脈內特征的識別已經(jīng)成為一項緊迫而嚴峻的任務。近年來,在雷達信號脈內調制識別技術的研究領域,出現(xiàn)了許多較為新穎的識別算法和相關技術,主要包括瞬時自相關算法、瞬時頻率法、短時傅里葉分析、小波分析等[1-3]。上述這些方法在對線性調頻、相位編碼等信號進行脈內調制分析時,都取得了一定的效果,但都存在著缺陷[4,5]。

在目前的工程實踐當中,最為常用的脈內調制識別方法是瞬時自相關算法。該算法的原理簡單,易于工程實現(xiàn)。在簡單的信號環(huán)境下[6,7],該算法可以比較準確地識別出線性調頻信號、頻率編碼信號和相位編碼信號,在信噪比優(yōu)于10 dB的條件下,3種調制類型的識別率分別可以達到 97%、92%和91%。但是該算法的抗噪性能較差,隨著信噪比的降低,識別性能急劇下降;當信噪比降低至0 dB時,會產(chǎn)生嚴重的誤判,對線性調頻信號的識別率降為46%,而且無法對其它調制方式進行識別。

基于以上問題,本文通過分析不同調制方式在調頻斜率上的區(qū)別和特點,提出一種基于分數(shù)階傅里葉變換(Fractional Fourier Transform,FRFT)的脈內信號調制方式的識別算法。該算法可以在低信噪比下完成線性調頻信號、頻率編碼信號和相位編碼信號的識別,為日后的工程改進提供了一種新思路。

2 雷達信號的脈內特征

雷達信號的脈內特征可分為人為調制和附帶調制,本文研究的對象是人為調制。人為脈內調制包括頻率調制和相位編碼[2]。

2.1 頻率調制信號

為了提高距離分辨能力,常利用各種頻率調制方式來增大雷達信號的帶寬。頻率調制的方式較多,本文主要考慮在雷達信號中經(jīng)常使用到的線性調頻信號和頻率編碼信號。

線性調頻脈沖信號是一種脈內頻率調制信號。設初始頻率為f0,脈寬為 tp,帶寬為B,調頻斜率為k,幅度為A,線性調頻脈沖信號s(t)可以表示為

線性調頻信號的時域波形及其頻譜如圖1所示。

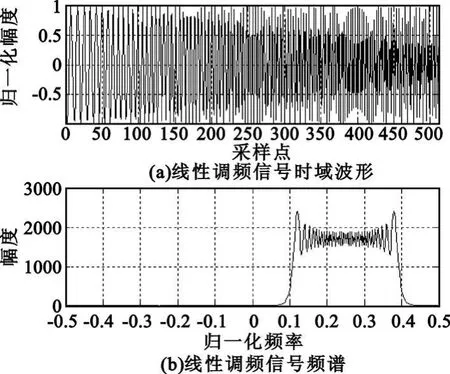
圖1 線性調頻信號的時域波形及頻譜Fig.1 Time domainwaveform and spectrum of LFM

頻率編碼信號可以看作是脈內離散頻率調制信號,頻率編碼信號的解析表達式如下:

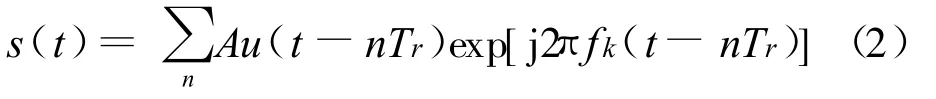
式中,fk為頻率碼組,子碼寬度為 Tr,幅度為 A。圖2為頻率編碼信號的時域波形及其頻譜。

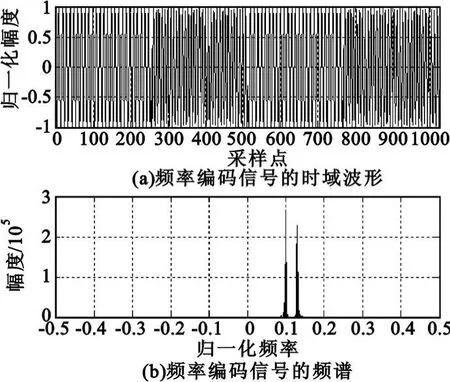
圖2 頻率編碼信號的時域波形及頻譜Fig.2 Time domain waveform and spectrum of frequency code signal

2.2 相位編碼信號

相位編碼信號由許多子脈沖構成,各個子脈沖的寬度相等,相位由一個編碼序列決定。如果子脈沖之間的移相值取0和π,即構成二相編碼信號;如果子脈沖之間的移相取兩個以上的移相值時,則構成多相編碼信號。相位編碼信號可以表示為

式中,f0為載頻,φ(t)為相位調制函數(shù)。圖3為二相編碼信號的時域波形圖及其編碼序列圖,其二進制編碼序列為[0101000011011]。

圖3 二相編碼信號時域波形及其相位編碼序列Fig.3 Time domainwaveform and phase-code sequence of two-phase-code signal

3 基于FRFT的脈內調制類型識別

3.1 FRFT的基本原理

設信號為s(t),其FRFT的定義為[8]

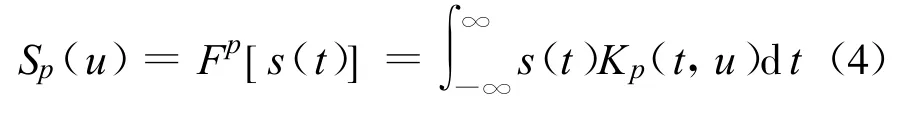
式中,p為 FRFT的階數(shù),Fp[]為 FRFT的算子,Kp(t,u)為FRFT的變換核,如式(6)所示:

近年來,人們對FRFT的快速數(shù)值運算進行了積極的研究,提出了很多FRFT的快速實現(xiàn)算法,其中H.M.Ozaktas[9]提出了分解型快速算法,該算法將FRFT分解為信號的卷積形式,其運算量小,在工程中得到了廣泛的應用。將分數(shù)階傅里葉變換的定義重寫如下:

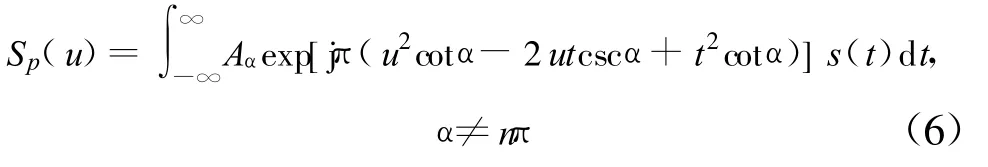
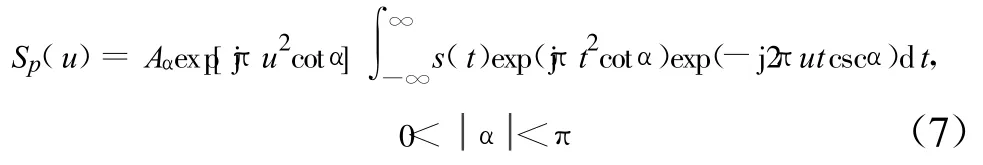
由上式可以看出,分解型快速算法將分數(shù)階傅里葉變換分為信號與線性調頻函數(shù)相乘、進行傅里葉變換、再與線性調頻函數(shù)相乘、乘以復數(shù)因子4個運算。利用以上過程,可以實現(xiàn)對FRFT的快速運算。若用FFT來實現(xiàn),則在信號長度為N時,計算復雜度僅為O(NlbN),這將大大提高運算速度[10]。

信號s(t)的分數(shù)階傅里葉變換Sp(u)可以看作是s(t)在以逆變核K-p(t,u)為基的函數(shù)空間上的展開,而該核是u域上的一組正交的chirp基[11]。線性調頻信號在適當?shù)姆謹?shù)階域中,將表現(xiàn)為一個沖激函數(shù),即分數(shù)階傅里葉變換的某個分數(shù)階域對給定的線性調頻信號具有很好的能量聚集特性,因此,FRFT多用于線性調頻信號的檢測。基于這個特性,本文將從線性調頻信號入手,逐步實現(xiàn)脈內調制類型的識別。

3.2 線性調頻信號的識別

通過觀察圖1～3發(fā)現(xiàn):線性調頻信號在其脈沖內部頻率發(fā)生了改變,變化的快慢由調頻斜率k決定;而頻率編碼信號和相位編碼信號在其碼元內部頻率不發(fā)生改變,可以認為它們是定頻信號,調頻斜率k為零。

信號經(jīng)FRFT后得到的模值為信號的時頻分布函數(shù)在與時間軸夾角成 α角度的軸線上的投影。若信號的調頻斜率與α滿足關系k=-cot α,即旋轉角度與信號調頻斜率匹配時,信號的時頻分布在 u軸的投影將出現(xiàn)一個尖峰,當旋轉角度與信號的調頻斜率不匹配時,信號變換為廣義的線性調頻信號,投影尖峰將不存在。因此,頻率編碼信號和相位編碼信號經(jīng)FRFT后,模值會在 α=π/2時(對應分數(shù)階次為1)出現(xiàn)尖峰,而線性調頻信號經(jīng)FRFT后得到的模值尖峰將不會出現(xiàn)在 α=π/2處[12]。

對線性調頻信號、頻率編碼信號以及相位編碼信號進行FRFT,取出每個分數(shù)階次中FRFT模最大值,這些最大值隨分數(shù)階次p的變化曲線如圖4～6所示。

圖4 線性調頻信號的FR FT模值隨分數(shù)階的變化曲線Fig.4 Curve of phase-code signal′s FRFT modular

圖5 頻率編碼信號的FR FT模值隨分數(shù)階的變化曲線Fig.5 Curve of phase-code signal′s FRFT modular

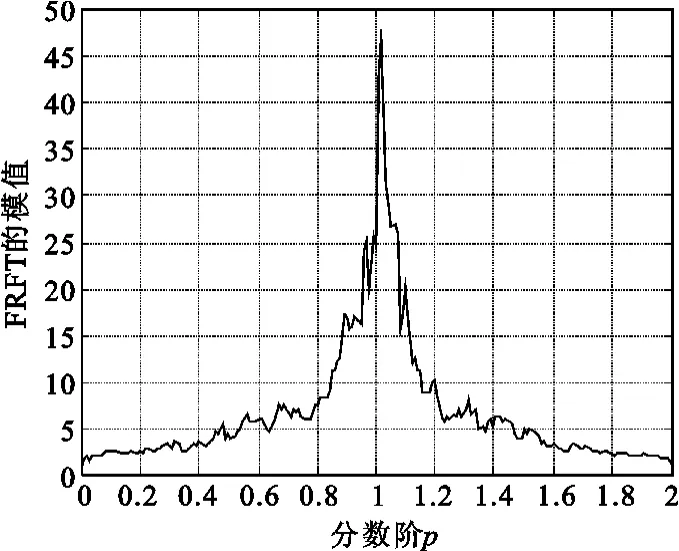
圖6 相位編碼信號的FRFT模值隨分數(shù)階的變化曲線Fig.6 Curve of phase-code signal′s FRFT modular

從圖中可以看出,曲線尖峰出現(xiàn)在不同的位置,這些位置反映了信號的調制類型。頻率編碼信號和相位編碼信號的FRFT模最大值在p=1處出現(xiàn)尖峰,且隨著p值偏離峰值點,幅度下降相對緩慢。而線性調頻信號的FRFT模最大值在與調頻斜率匹配的分數(shù)階次處出現(xiàn)尖峰,該峰值僅在對應的p值附近很窄的范圍內比較大,偏離峰值點后,幅值急劇下降。

此處,將頻率編碼信號和相位編碼信號統(tǒng)稱為編碼信號。從圖4～6中可以看出,線性調頻信號在p=1處的FRFT模最大值非常低,而編碼信號的FRFT模最大值在p=1處是明顯的尖峰,兩者幅度差距明顯。因此,依據(jù)信號在p=1附近FRFT模最大值的大小,可以實現(xiàn)線性調頻信號和編碼信號的區(qū)分。設信號在p=1附近的FRFT模最大值為S,設定門限St,當S>St時,將信號識別為編碼信號;當S≤St時,將信號識別為線性調頻信號。

3.3 編碼信號的識別

由于頻率編碼信號和相位編碼信號經(jīng)FRFT得到的模最大值在 p=1處同樣存在峰值,因此本文對上述兩種信號在分數(shù)階次p=1處進行FRFT。圖7和圖8為在信噪比為0 dB時,頻率編碼信號、相位編碼信號在 p=1處FRFT的波形圖。從圖中可以看出,相位編碼信號的FRFT僅存在一個峰值,頻率編碼信號的FRFT存在多個峰值,且峰值個數(shù)等于信號分布的頻率點數(shù)。根據(jù)峰值個數(shù)的不同,我們可以識別出這兩種編碼信號。當信號在p=1處的FRFT波形存在有兩個以上的峰值時,信號被識別為頻率編碼信號;當僅存在一個峰值時,信號被識別為相位編碼信號。

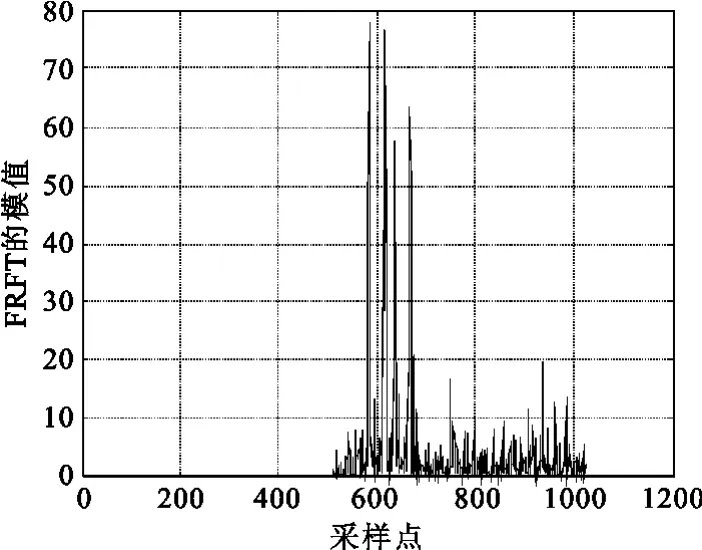
圖7 頻率編碼信號在 p=1處的FRFT波形Fig.7 Waveform of frequency code signal′s FRFT modular with p=1

圖8 相位編碼信號在 p=1處的FRFT波形Fig.8 Waveform of phase code signal′s FRFT modular with p=1

4 算法性能分析

為了驗證算法的有效性,本文在信噪比為-4～10 dB的條件下,對隨機生成的線性調頻信號、頻率編碼信號和相位編碼信號進行FRFT,并依據(jù)本文設計的方法進行調制方式識別。每個信噪比整數(shù)值點進行Monte-Carlo實驗500次,繪制識別概率曲線,如圖9所示。

圖9 識別概率曲線Fig.9 Curve of recognition probability

觀察圖9中的曲線可以發(fā)現(xiàn),在信噪比降為-2 dB時,FRFT仍可以較好地完成脈內信號調制方式的識別。該條件下,頻率編碼信號的識別率最高,接近90%;線性調頻信號次之,達到了85%;而相位編碼信號的識別率最低,為77%。產(chǎn)生錯誤的原因是由于噪聲的影響,隨著信噪比的降低,信號在p=1附近的FRFT模值不能正確反映出信號的頻率調制特征,造成識別錯誤。由于相位編碼信號在其相位突變處存在頻率的變化,在噪聲的影響下,信號在p=1處的FRFT波形出現(xiàn)多個峰值,因此被識別為頻率編碼信號。而頻率編碼信號可以看作是多個常規(guī)信號的組合,因而在識別過程中受噪聲影響較小,識別率較高。

將基于FRFT的調制方式識別結果與瞬時自相關算法的識別結果作比較,表1列出了信噪比為0 dB時兩種算法的識別結果,從另一個角度驗證了本文算法的有效性。通過本文的識別方法,可以大幅度提高低信噪比下線性調頻信號的識別概率(在0 dB時,從46%提高到了88%),并完成了低信噪比下頻率編碼信號和相位編碼信號的識別。

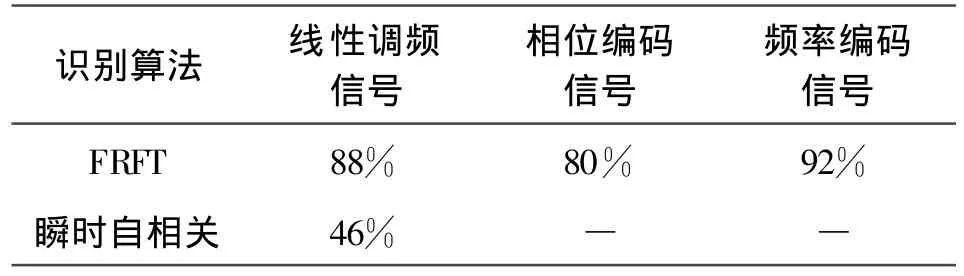
表1 信噪比為0 dB時脈內信號調制方式的識別概率Table 1 Recognition probability of radar intra-pulse signals modulation when SNR=0 dB

綜上,本文設計的基于FRFT的脈內信號調制方式識別方法能夠完成對3種常用脈內調制方式的識別,在信噪比優(yōu)于-2 dB的條件下,達到了較好的識別效果,具有一定的抗噪性能。識別過程中,所采用的FRFT僅是在分數(shù)階數(shù)p=1上進行的,省去了對所有分數(shù)階域的搜索,節(jié)省了識別時間和存儲空間,提高了效率。

5 結束語

雷達信號的脈內調制方式識別是參數(shù)估計的前期工作,其意義重大。現(xiàn)代雷達信號的脈內調制方式趨于復雜化、多樣化,本文所針對的3種調制方式屬于初級的脈內調制方式特征,它們還可以進一步劃分為二相編碼信號、四相編碼信號、V型調頻信號等細微的脈內調制方式[1]。從這個角度來講,本文設計的識別方法是一種初級的識別模型,在此基礎上如何進一步識別脈內信號的細微特征,構建一個完整的脈內調制特征識別系統(tǒng),將是本文后續(xù)工作的研究重點。

[1]Mark A Richards.雷達信號處理基礎[M].北京:電子工業(yè)出版社,2008.Mark A Richards.Fundamentals of Radar Signal Processing[M].Beijing:Publishing House of ElectronicsIndustry,2008.(in Chinese)

[2]Richard G Wiley.ELINT:The Interception and Analysis of Radar Signals[M].Norwood,MA:Anech House,2006.

[3]Kawalec A,Owczarek R.Radar emitter recognition using intrapulse data[C]//Proceedings of the 15th International Conference on Microwaves,Radar andWireless Communications.Warsaw,Poland:IEEE,2000:435-438.

[4]姜勤波,馬紅光,楊利鋒.一種新的雷達脈沖信號的非匹配檢測算法[J].現(xiàn)代雷達,2006,28(11):36-40.JIANG Qin-bo,MA Hong-guang,YANG Li-feng.A Novel Nonmatched DetectionAlgorithm of Radar Pulse Signal[J].Modem Radar,2006,28(11):36-40.(in Chinese)

[5]李振興,張國毅.基于調制域的雷達信號脈內特征提取新方法[J].電訊技術,2010,50(12):69-74.LI Zhen-xing,ZHANG Guo-yi.A New Intra-pulse Feature Extraction Approach for Radar Signals Based onModulation Domain[J].Telecommunication Engineering,2010,50(12):69-74.(in Chinese)

[6]鄒順.雷達信號分選與細微特征分析[D].西安:西北工業(yè)大學,2006:46-50.ZOU Shun.Analysis of Fine—feature for Radar Signal[D].Xi′an:Northwestern Polytechnical University,2006:46-50.(in Chinese)

[7]ZHANG Ge-xiang,HU Lai-zhao,JIN Wei-dong.Resemblance coefficient based intra pulse feature extraction approach for radar emitter signals[J].Chinese Journal of Electronics,2005,14(2):337-341.

[8]唐向宏,李齊良.時頻分析與小波變換[M].北京:科學出版社,2008.TANG Xiang-hong,LI Qi-liang.Time-frequency Analysis and Wavelet Transform[M].Beijing:Science Press,2008.(in Chinese)

[9]HaldunM Ozatkas,OrhanArikan,Alper M Kutay.Digital Computation of the Fractional Fourier Transform[J].IEEE Transactions on Signal Processing,1996,44(9):2141-2150.

[10]趙興浩,陶然,鄧兵,等.分數(shù)階傅里葉變換的快速計算新方法[J].電子學報,2007,35(6):1089-1093.ZHAO Xing-hao,T AO Ran,DENG Bing,et al.Ne w Methods for Fast Computation of Fractional Fourier Transform[J].Acta Electronica Sinica,2007,35(6):1089-1093.(inChinese)

[11]LIU Feng,HUANG Yu,TAO Ran,et al.Chirp-Rate Resolution of Fractional Fourier Transform inMulti-component LFM Signal[J].Journal of Beijing Institute of Technology,2009,8(1):74-78.

[12]QI Lin,TAO Ran,ZHOU Si-yong.Rejectionof Linear FM Interference in DSSS System Based on Fractional Fourier Transform[J].Journal of Beijing Institute of Technology,2005,14(2):158-161.