基于HFSS設計同軸腔調諧濾波器

賈建蕊,韓 軍

(中國電子科技集團公司第五十四研究所,河北石家莊050081)

0 引言

調諧濾波器既能夠實現頻率抗干擾又能夠滿足最佳收、發濾波器要求,其通帶頻率能夠隨著工作頻率要求的改變而相應改變,在通信系統抗干擾技術中的作用舉足輕重。腔體調諧濾波器設計主要存在以下2個難點:①在調諧過程中,濾波器的響應特性和絕對帶寬隨著中心頻率的變化而發生顯著變化,通帶內插損增大,阻帶抑制度下降;②在調諧過程中,中心頻率隨著耦合結構的變化呈非線性變化,耦合結構難以實現。在此根據濾波器設計的基本原理,利用HFSS進行預仿真,很好地克服了上述2個缺點,實現了實例設計。

1 總體設計

以L波段濾波器設計為例,主要設計參數如表1所示。

由于所設計的調諧濾波器的調諧范圍為1 300～1 600MHz,為了便于照顧整個頻段的相對帶寬,選擇中間點1 450 MHz為設計頻點。利用網絡綜合法,選取切比雪夫函數作為逼近函數,切比雪夫響應函數[1]。在通帶內是等波紋型的,通帶內損耗LAr要足夠小,取LAr=0.03。經查表計算確定濾波器階數n=4,對應的低通原型參數 gn可通過公式計算得:g0=1,g1=0.868 1,g2=1.275 4,g3=1.506 2,g4=0.735 1,g5=1.181 0。

表1 濾波器的技術參數

腔間耦合系數k及外界Qe值[2]的理論值可由式(1)和式(2)得到:

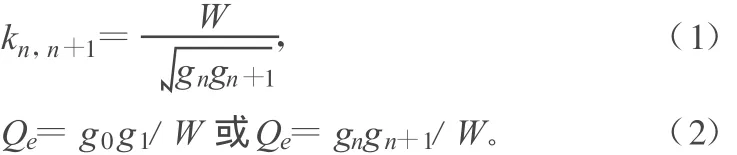
根據式(1)畫出整個調諧頻段的耦合系數k的曲線,如圖1所示,在后續仿真中,為了保證在整個頻段內絕對帶寬不變,要盡量使仿真曲線逼近圖1中的理論值曲線。

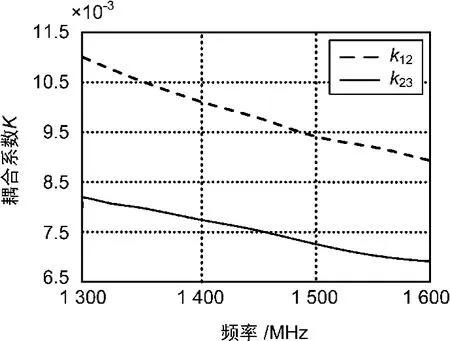
圖1 腔間耦合系數隨頻率變化曲線

根據式(2)計算設計頻點的外界 Qe值:Qe=109.17,以初步確定耦合環的位置及大小。畫出整個調諧頻段的Qe值曲線,如圖2所示,作為后續仿真中的標準。

圖2 外界 Q值隨頻率的變化曲線

2 微波結構設計及其仿真

2.1 腔體結構

根據工作頻段低和功率容量不大以及電調濾波器的實現難易程度,腔體選擇 λ/4同軸腔結構,通過改變內導體長度來改變工作頻率。工作頻率隨著內導體長度的增加,由高到低逐漸變化。

為了方便加工和調試,同軸腔的結構為外腔為方形內導體為圓形,并通過在腔內表面鍍銀來減小損耗增加Qe值。外腔橫截面為邊長為30 mm的正方形,當同軸腔的外、內導體直徑比為3.591時,同軸腔的Qe值最高,即同軸腔導體損耗最小,為了保證高Qe值和加工方便,選擇內導體直徑為10 mm。內導體頂端與腔體壁之間距離10 mm以上時,產生的端電容很微弱,對頻率不會有影響,因此腔體的高度選擇為65 mm。

在HFSS中建立單諧振腔模型,用本征模解求解仿真,仿真結果如圖3所示。根據仿真結果可以看到,調諧范圍大致在41～53 mm,可覆蓋1 300～1 600 MHz,調程約有 12 mm,每 25 MHz調程是0.1 mm,按照目前的加工情況,能夠較好地滿足調諧精度。

圖3 內導體與諧振頻率的關系

2.2 腔間耦合結構的選擇

耦合結構是整個濾波器的最關鍵部分。在微波腔體濾波器中,腔間的耦合大多采用側面上開孔進行耦合,在以同軸腔做為諧振單元的可調濾波器中,級間的耦合大多以腔間的側面孔來進行耦合,孔的形狀主要是圓形和矩形。采用矩形孔作為調諧濾波器的腔間耦合結構不僅可以極大地擴大濾波器的調諧范圍,保證其通帶帶寬在較大的調諧范圍內基本不變,而且還可以消除大帶寬濾波器中的大波紋效應。為了保證微波濾波器的調諧范圍及其在調諧范圍內通帶寬度基本不變,采用矩形孔作為調諧濾波器的耦合結構。

2.2.1 耦合孔位置的計算[3]

由于設計的是寬頻段調諧濾波器,耦合孔的位置應該位于電磁場最不敏感的地方。對于矩形耦合孔,其帶寬與調諧頻率的關系為:

式中,c為真空中光速;D為同軸腔體直徑;M為孔上的磁化強度;l為孔中心點距短路端的距離。

在頻點1 450 MHz,l=20.69 mm。

2.2.2 耦合孔大小的計算

根據前面計算的頻點的耦合系數,可以由下面公式計算腔間耦合孔的具體大小:

式中,r為耦合孔半徑;λ0為工作波長;b/a為內外導體半徑之比;l為耦合孔中心到短路端距離;D為外導體邊長;θ為電長度。

計算一腔、二腔和二腔、三腔之間耦合孔半徑分別為7.67 mm和7.08 mm,在同軸腔諧振器中,側面上的等面積小孔耦合近似相等,把圓孔轉化為等面積的方形孔,并計算出其邊長分別為13.6 mm和12.54 mm。

2.2.3 耦合孔的仿真

按照上面計算數據,在HFSS中建立2個相鄰的諧振腔模型,對耦合系數和頻率之間的關系進行全頻段仿真,發現按照計算出的耦合孔建模,整個頻段內耦合值都達不到理論值要求,尤其是低端相差較大。

對耦合孔的2個邊長進行漸近優化仿真,選擇耦合值最接近理論值的孔,優化后其仿真耦合系數曲線如圖4所示。可以看出優化后仿真結果與理論值相比,在低端比理論值略小,在高端比理論值略大,但從全頻段來看,已經和理論值曲線很接近。

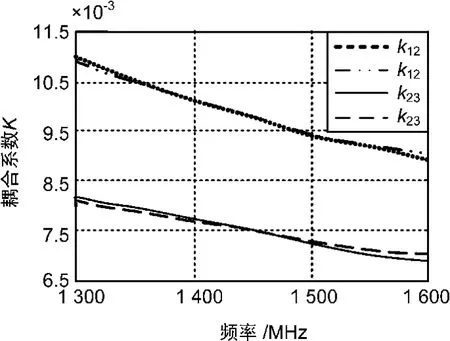
圖4 仿真耦合系數曲線

2.3 輸入輸出耦合結構的選擇

輸入、輸出端的耦合形式主要是環耦合,環的形狀主要有半圓環、矩形環和三角環[3]。矩形環耦合電抗的頻率特性比半圓環平坦,而且在頻率的高端也能提供足夠的耦合量,較之三角環和不規則形狀,尺寸比較容易確定。因此選擇矩形環作為輸入、輸出耦合結構,其結構圖如圖5所示。

耦合環的長度Δl的取值一般為λ/12～λ/6,選取Δl,利用式(7)[3]可計算耦合環的位置La。

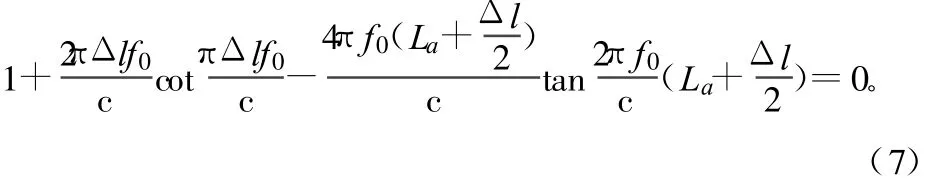
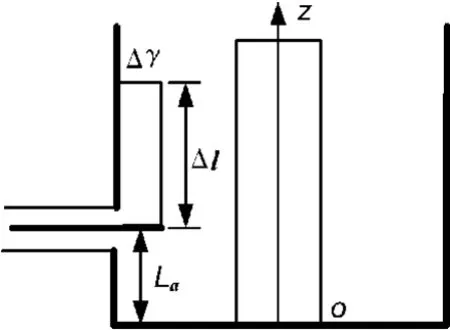
圖5 矩形耦合環結構

式中,Δl、Δγ和La的含義如圖5所示;c為真空中光速;f0為中心頻率(頻點),將 Δl和La代入式(8)[3],可求出Δγ。

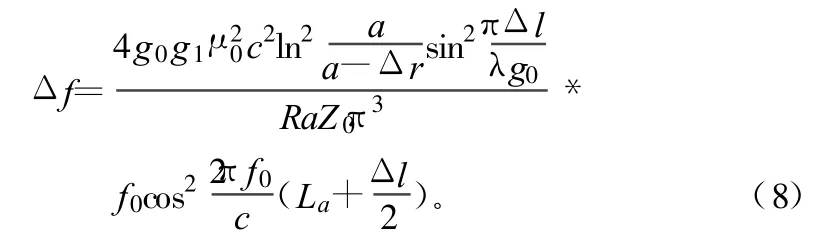
式中,Z0為諧振腔的特性阻抗;Ra為同軸電纜的輸入電阻。由式(8)計算得La=11 mm,Δγ=2 mm,Δl=31 mm。

按照計算數據,在HFSS中對其建模,用激勵解求解整個頻段內有載品質因數Q值,與理論值圖2進行對比,仿真結果與理論值有一定誤差。對耦合環優化后,結果與理論值較吻合。

2.4 綜合建模仿真

將上述確定的濾波器結構綜合起來,在HFSS中建立整個濾波器模型進行仿真優化。濾波器響應特性如圖6、圖7和圖8所示。

由圖6、圖7和圖8可以看出,在低端絕對帶寬比高端略微小一點,但總體來看,所設計濾波器能夠較好地滿足設計指標要求。

圖6 低端仿真結果

圖7 中間頻段仿真結果

圖8 高端仿真結果

3 結束語

以傳統的理論設計方法來設計同軸腔調諧濾波器,耦合結構的計算沒有非常精確的計算公式,需要經過多次對實物的修改和測試才能達到設計指標,而用HFSS仿真軟件結合設計原理的方法,以上過程只需在電腦上模擬仿真完成,最終能夠精確設計調諧濾波器。該設計方法提高了設計精度,加強了設計規范,縮短了設計周期,具有很高的參考價值。

[1]甘本祓,吳萬春.現代微波濾波器的結構與設計[M].北京:科學出版社,1973.

[2]王清芬,馬延爽.耦合系數法設計微波帶通濾波器及CAD實現[J].無線電通信技術,2008,34(1):43-44.

[3]姚 毅.寬范圍調諧微波濾波器耦合結構的研究[D].成都:電子科技大學碩士論文,1993:48-49.