基于遺傳算法與約束矩陣的工藝路線優化方法研究

王 軍 孟慶智

(燕山大學機械工程學院，河北秦皇島066004)

工藝路線的優化是CAPP(計算機輔助工藝過程設計)系統的關鍵技術與難點之一，是衡量CAPP系統智能化和實用化的一個重要標志，它在很大程度上決定了CAPP系統的應用水平［1］。其主要任務是按照工藝約束規則和一定的優化目標，對工件所有加工特征的加工方法進行排序，將得到的最優加工序列作為工件的工藝路線［2－3］。

工藝路線優化問題與其他優化問題不同，它求解的不是值優化而是排序優化，而且排序過程與機床、刀具、夾具、約束之間存在各種可能的聯系，這使得工藝路線排序成為一個極其復雜的組合優化問題，其優化目標和約束條件都難以用明確的解析式表達，因此工藝路線的決策和優化問題很難用傳統的優化算法來解決［4－5］。本文采用遺傳算法進行工藝路線的優化決策。它以優化變量的某種形式的遺傳編碼為運算對象，以基因交叉重組和變異為基礎進行全局搜索，不僅并行性高、魯棒性強，而且個體的適應度評價也可以不依賴于目標函數的恰好估值。

本文在對工藝路線優化問題進行分析的基礎上，建立工藝決策的數學模型，并利用約束矩陣來描述工藝約束關系，而且約束矩陣由系統自動生成，設計了用于保證加工元序列的滿足約束關系的算法，對基于遺傳算法的工藝路線優化決策方法進行了研究。

1 工藝路線優化決策的問題描述

進行工藝設計，首先要根據工件各特征的加工屬性(形狀、尺寸、公差和表面粗糙度)確定其加工方法，然后對所有特征的加工方法進行組合排序，這個過程就是工藝路線的優化過程。為了方便工藝路線的描述和遺傳操作，將工件特征的某個加工操作定義為加工元，由加工元編號、加工特征、加工方法，以及所使用的機床、刀具、裝夾方案組成。將加工元表示為

Op=(ID，Feature，Process，Machine，Tool，Setup)

其中:ID、Feature、Process、Machine、Tool、Setup 分別為加工元編號、加工特征、加工方法、所需的機床、刀具和裝夾方案。

設 O={Op1，Op2，…，Opn}為完成工件加工的所有加工元的集合。把工件某一工藝路線表示為

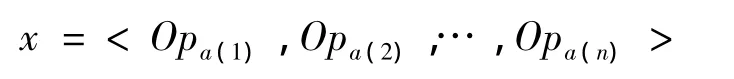
其中:{Opa(1)，Opa(2)，…，Opa(n)}={Op1，Op2，…，Opn}，x為以Opa(1)開始、Opa(n)結束的加工元序列。

工藝路線優化的過程實際上就是根據當前生產環境，生成一個最優化或接近最優化的加工元序列的過程。在生產過程中，常根據實際需要確定目標函數，例如生產成本最低、加工時間最短等，對工藝路線進行評價，那么可以確定目標函數的形式為minF(xi)，其中，F(xi)為xi這一工藝路線的優化評價函數。

在工藝路線的優化決策過程中，還必須滿足工藝約束，主要指對優化排序具有重要影響的加工方法之間的優先關系約束。將約束信息用矩陣A［n］［n］表示。

所謂最優工藝路線是指在滿足工藝約束的條件前提下，目標函數值最優的工藝路線。其中工藝約束主要是指對工藝路線的優化排序具有重要影響的加工方法之間的優先關系約束。在本文中將工藝約束信息用矩陣 A［n］［n］表示。

基于以上分析，工藝路線優化問題的數學模型可描述為:對于工件的加工元集合 O={Op1，Op2，…，Opn}，尋找一條加工工藝路線 x=＜Opa(1)，Opa(2)，…，Opa(n)＞，使其滿足工藝約束 A［n］［n］，且目標函數值最優，即minF(x)。

工藝路線的優化過程實際上就是將約束逐個作用到加工元集合上，使得加工元在一定的排列順序下，目標函數值最優。

2 工藝約束及其處理方法

2.1 工藝約束的描述

制定合理的工藝路線必須考慮工件加工特征之間和加工方法之間的優先關系約束，主要包括以下幾個方面:

(1)先粗后精 對于每個特征，粗加工工序應安排在精加工工序之前進行;對于整個工件，所有的粗加工工序應安排在所有精加工工序之前進行。

(2)先主后次 即先安排工作表面和裝配表面的加工，后安排次要表面的加工，而且次要表面安排在最后精加工或光整加工之前。

(3)先基準后其他 作為基準的特征應先加工，然后才加工其他表面。如當兩個特征之間存在形位公差時，包含基準的加工特征應當首先加工;加工階梯軸時，端面特征作為測量基準優先于外圓面加工。

(4)非破壞性約束 保證后面的加工不會破壞在前面加工過程中產生的屬性。例如在一個圓柱上加工螺紋和倒角時，倒角應先于螺紋加工。

(5)依賴約束 若某一特征的存在依賴于另一特征，則另一特征先于此特征加工。例如在一個平面上有一個孔特征，那么面特征要先于孔特征加工。

工藝路線必須滿足上述約束規則。在約束規則的作用下，加工元之間的優先關系約束表現為執行的先后次序。由于定性的、描述性的約束信息在計算機處理時比較復雜，不便于計算機的底層推理和簡化計算，本文通過工藝約束矩陣的方式描述加工元之間的優先關系約束，將定性的優先關系約束信息轉化為定量的、數字化的矩陣。

約束矩陣用A［n］［n］來表示，n表示加工元的個數。矩陣中元素aij代表兩加工元之間的先后關系，元素值按以下規則進行轉換:

2.2 約束矩陣的自動生成

系統根據優先關系約束原則，并結合加工元中的特征信息、加工方法信息、裝夾方案等信息，對加工元進行分類，屬于不同類別間的加工元具有相應的優先關系，系統按照約束矩陣轉換原則將矩陣中相應的元素賦值為1。

以先粗后精原則為例，首先遍歷所有加工元，根據各加工元的加工方法，將屬于粗加工階段、半精加工階段和精加工階段的加工元劃分到其相應集合;由先粗后精原則，有粗加工階段加工元集合中的元素優先于半精加工階段加工元集合中的元素，半精加工階段集合中的元素優先于精加工階段加工元集合中的元素;最后，根據約束矩陣轉換原則將以具有優先關系的兩個加工元為下標的元素賦值為1。在處理完由所有原則產生的加工元之間的優先關系后，工藝約束矩陣自動生成。

3 基于遺傳算法的工藝路線優化過程

3.1 基因編碼

基因編碼是應用遺傳算法的第一步，常用的二進制編碼無法表達工藝路線的排序優化問題。本文采用自然數字鏈進行基因編碼。為便于遺傳操作和約束矩陣的生成，將每一個基因對應工件加工元集合中的一個加工元，因此每個基因由6部分組成，分別對應加工元的6個組成部分。在程序中基因用如下的結構體來描述。其中加工元編碼與自然數字鏈一一對應，它是區分加工元的標志，代表加工元進行遺傳操作;基因中其他部分代碼也都用兩位十進制數表示，程序運行過程中需要根據這些代碼確定加工元間的優先關系和計算染色體的適應度值。

3.2 初始種群的產生

初始種群是根據工件加工元集合隨機生成的一組確定數量的加工元序列。初始種群中可能存在無效的即不滿足優先關系的加工元序列，需通過約束矩陣和加工元序列調整算法將它們轉化為有效的加工元序列，從而使初始種群中的染色體均符合優先關系約束。

3.3 適應度函數的確定

在工藝設計中，工藝路線一般是通過加工成本最低、加工時間最短等作為評價指標。本文以加工成本最小作為工藝路線的優化目標。加工成本包括機床成本、刀具成本、機床變換成本、刀具變換成本和裝夾變換成本。對一個工件的工藝過程來說，在確定各特征的加工方法及其使用的制造資源后，機床成本和刀具成本對每一種加工元序列都是一樣的。對不同的加工元序列，加工成本的不同主要體現在機床變換成本、刀具變換成本和裝夾變換成本。因此本文以總變換成本最小作為工藝路線的優化目標。總變換成本C、機床變換成本CM、刀具變換成本CT和裝夾變換成本CS分別表示如下

其中，N 表示加工元集合中加工元的個數;M［i］［i+1］、S［i］［i+1］、T［i］［i+1］分別表示某一加工元序列中第 i個加工元與第i+1個加工元的機床變換成本、裝夾變換成本和刀具變換成本，在本文中設 M［i］［i+1］、S［i］［i+1］、T［i］［i+1］分別為 20、8、1;mi、si、ti分別表示第 i個加工元中所使用的機床、裝夾方案和刀具。對于以上各式有

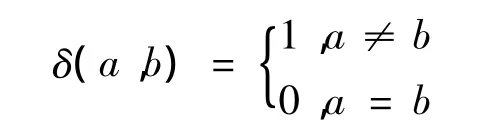
最優的工藝路線是具有最小變換成本的加工元序列，而遺傳算法是根據適應度對個體進行評價的，適應度值越大者為較優的個體，因此有必要建立適應度函數與目標函數的映射關系:

其中:Lj為第j條染色體，Cmax為工藝路線總變換成本的理論最大值，Cj為第j條工藝路線的總變換成本。

3.4 選擇

采用排序選擇算法和最佳個體保護策略相結合的選擇方法。排序選擇算子，即對種群中的個體按照適應度值的大小進行排序，然后基于一定的比例，將排在前面具有較高的適應度值的個體復制2份，中間具有稍高適應度值的染色體復制1份，排在最后適應度值較低的個體不復制，所有復制得到的個體構成交配池。排序選擇法保證了參與后代的繁衍和進化的是種群中的優良個體［6］。

采用最佳個體保護策略，是為了防止進化過程中最優個體由于參與交叉和變異而被破壞。即每次計算的最優個體除作為交配池的種子之外，還直接作為子代個體。最佳個體保護策略保證了每次計算結果至少不會比上一次差，使進化的方向總是向著最優值的方向逼近。

3.5 交叉

為保證交叉后的染色體有效，采用兩點交叉的方式進行交叉運算。具體步驟如下:

(1)首先在交配池中隨機選取兩個個體作為父代染色體P1、P2，并隨機生成兩個交叉點，這樣父代染色體被分為左半部分、中間部分和右半部分。

(2)將P1的左半部分和右半部分分別復制到子代染色體C1的左右兩半部分。

(3)在P2中劃掉與P1的左半部分和右半部分完全相同的基因，將P2中剩余的基因按照它們原來的順序依次復制到C1的中間部分，這樣就形成C1。

(4)采用同樣方法得到子代染色體C2。圖1為交叉過程。

由于父代染色體是有效的染色體，采用兩點交叉方法生成的子代染色體也是滿足優先約束的，因此不需要調整加工元序列。

3.6 變異

本文采用隨機交換染色體中的2個基因代碼的位置的變異運算。即在一定的變異率下，選擇一部分染色體，在單個染色體內部隨機進行2個基因的交換形成新的個體，如圖2所示。

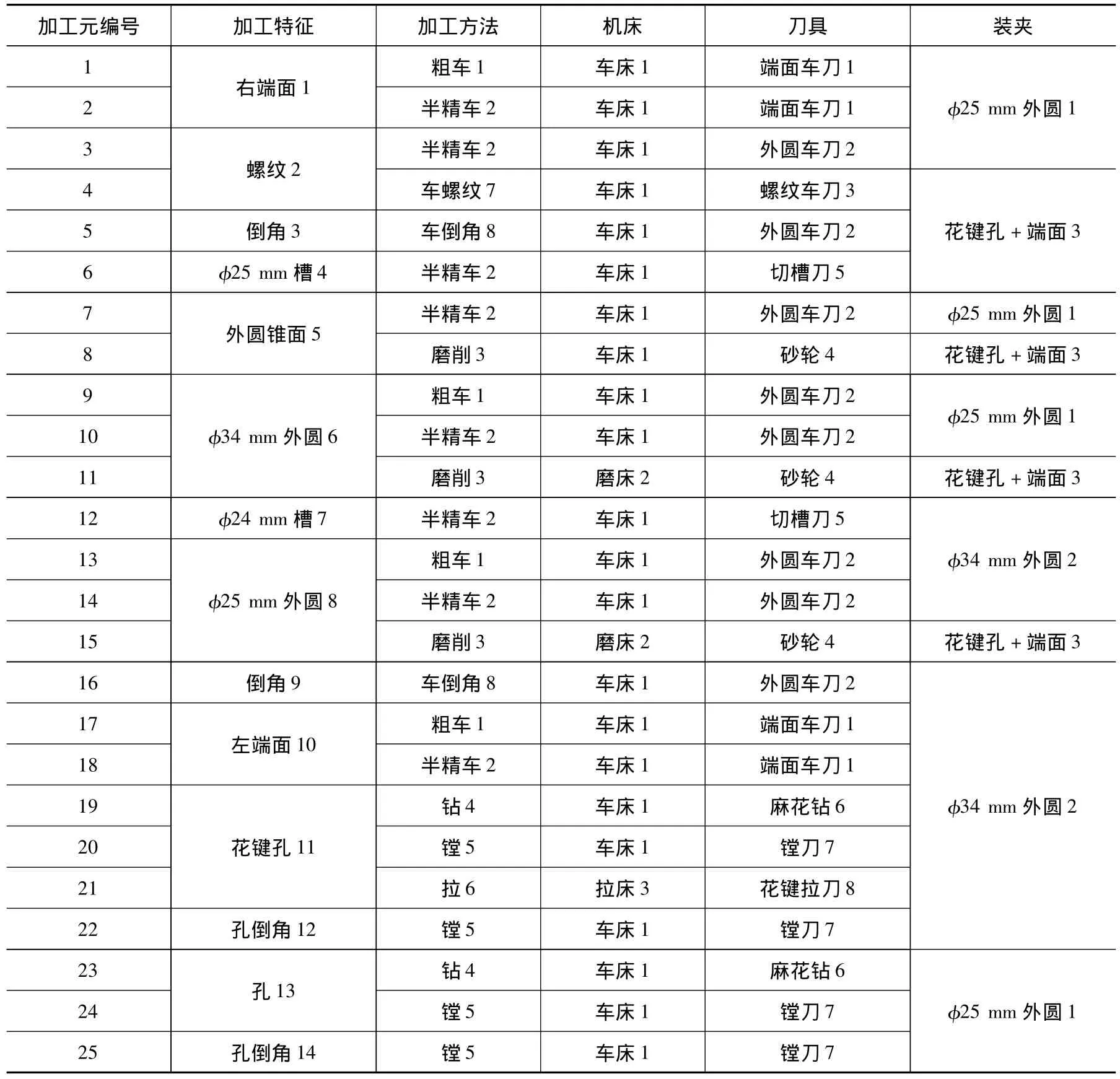
表1 基因編碼

由于交換2個基因后，可能會出現無效的即違反優先關系約束的染色體，因此，變異運算完成后，要判斷新生成的個體是否有效。如果無效，則需通過調整算法將其轉化為有效的染色體。在這里，只需調整兩個交換點之間的基因序列，因為交換位置以外的基因序列本身就滿足優先關系約束，只要保證交換點之間序列的有效性，就能保證整條染色體的有效性。

3.7 加工元序列有效性檢驗與調整算法

在初始種群生成和遺傳操作過程中，生成的加工元序列可能會不滿足優先關系約束。為了在遺傳算法運行過程中保證個體的有效性，須根據工藝約束規則確定的加工元優先關系約束矩陣對個體進行有效性檢驗和調整。

設某一個體表示的加工元序列為

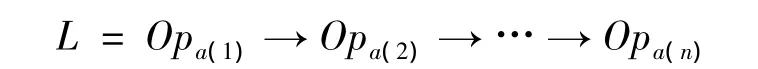
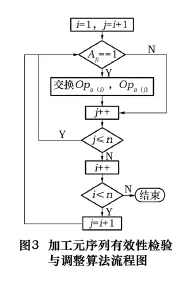
圖3為算法流程圖。

步驟1:遍歷加工元序列L，從Opa(1)到Opa(n)，設i=1，j=i+1;

步驟2:搜索約束矩陣，如果Aji=1，說明加工元Opa(j)優先于加工元Opa(i)，應互換Opa(i)和Opa(j)，并使j++。否則，直接使j++。

步驟3 判斷是否j≤n，如果真，則轉到步驟2;否則令i++，并轉到步驟4。

步驟4 如果 i＜n，令j=i+1，轉到步驟2，否則結束。

3.8 終止條件

為保證遺傳算法在保證具有較優解的基礎上正確退出，以連續迭代 1 000次，或最優個體的適應度值連續迭代200次保持不變為終止條件。

計算終止后，輸出適應度值最大個體對應的加工元序列，作為工件的工藝路線。

4 應用實例

以圖4所示的花鍵套工件為例來說明該算法的實現過程。

首先在明確各特征及其加工方法、定位基準和制造資源之后，進行基因編碼，如表1所示。

然后根據特征、加工方法、裝夾方案等信息和優先關系約束原則，確定加工元之間的優先關系，并建立描述優先關系的工藝約束矩陣。

設種群規模為80，交叉率為0.8，變異率取0.2，迭代次數達到1 000或最高染色體的適應度值經過200次迭代仍保持不變為終止條件。經過1 000次迭代，程序運行停止，得到適應度值最高的染色體的適應度值為393，其對應的工藝路線如表2所示。其中更換機床的次數為3次，更換夾具的次數為4次，更換刀具的次數為16次。該優化結果表明基于遺傳算法和約束矩陣的工藝路線優化算法是可行有效的。

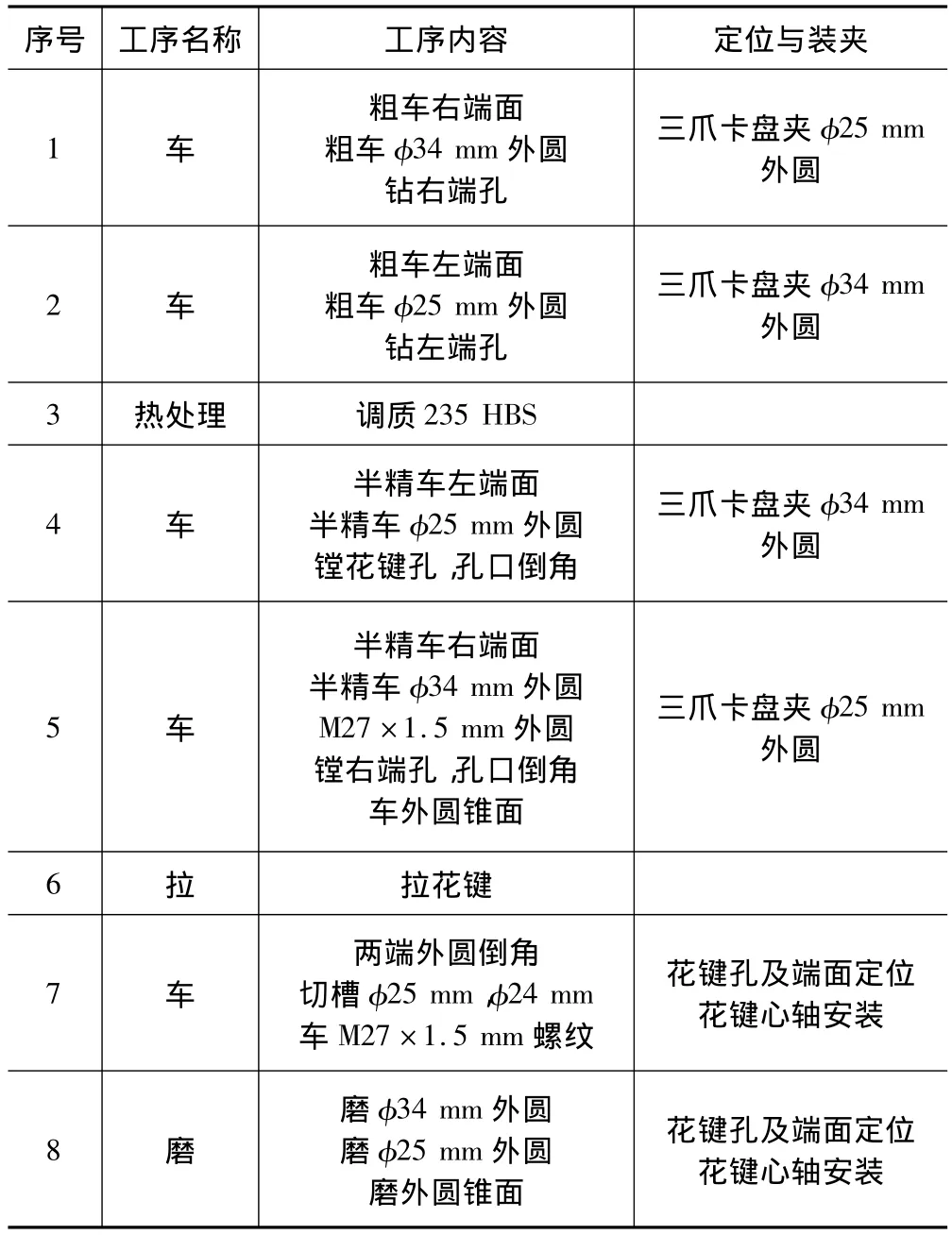
表2 最大適應度值染色體對應的工藝路線

5 結語

本文提出的基于遺傳算法和約束矩陣的工藝路線排序優化方法，是CAPP中解決工藝路線優化問題的有效實用方法。利用約束矩陣來描述加工元之間的優先關系，并由系統自動生成約束矩陣，開發了不依賴于特定規則的加工元序列有效性檢驗與調整算法，以總變換成本最小為優化目標，利用改進的遺傳算法對工藝路線排序進行啟發式全局尋優，實例驗證了該算法的可行性和有效性。

［1］邵新宇，蔡力鋼.現代CAPP技術與應用［M］.北京:機械工業出版社，2004.

［2］朱海平，肖詩旺，黃剛.基于遺傳算法的工藝過程排序研究［J］.華中科技大學學報:自然科學版，2006，34(3):50－53.

［3］劉連發，張振明，田錫天，等.基于遺傳算法的工藝路線優化決策方法研究［J］.機械制造，2008，46(526):59－62.

［4］王忠賓，王寧生，陳禹六.基于遺傳算法的工藝路線優化決策［J］.清華大學學報:自然科學版，2004，44(7):988－992.

［5］張國輝，蔡力鋼，高亮，等.基于改進遺傳算法的工藝路線優化［J］.機械設計與制造，2006(8):14－16.

［6］任慶生，葉中行，曾進，等.對常用選擇算子的分析［J］.上海交通大學學報，2004，34(4):564 －566.