規則波中船舶復原力和參數橫搖研究

魯 江,馬 坤,黃武剛

(大連理工大學工業裝備結構分析國家重點實驗室船舶工程學院,遼寧 大連 116024)

規則波中船舶復原力和參數橫搖研究

魯 江,馬 坤,黃武剛

(大連理工大學工業裝備結構分析國家重點實驗室船舶工程學院,遼寧 大連 116024)

為研究規則波中船舶復原力變化規律及其對參數橫搖的影響,首先,基于切片理論求解出船舶無橫傾時在波浪中時間序列垂蕩和縱搖運動,確定出波面與船體的相對位置;其次,利用三個坐標系之間的轉換關系進而確定規則波中船體各橫剖面左右舷與波面瞬時交點,求得各浸水剖面面積;然后對波浪壓力沿船長濕表面積分,得出規則波中船舶復原力的Froude-Krylov部分。同時,利用作用在橫傾船舶上的輻射力和繞射力,求出規則波中船舶復原力輻射力和繞射力部分。在復原力計算的基礎上,確定一個參數橫搖模型,實現波浪中參數橫搖計算。以一艘集裝箱船為例,研究了規則波中復原力變化以及參數橫搖規律,復原力變化幅度是影響參數橫搖的一個重要因素。

復原力;參數橫搖;Froude-Krylov假說;規則波;船舶

Abstract:In order to study the roll restoring variation inwaves and the effect of restoring variation on parametric rolling,firstly,the relative position of ship to waves is determined with heave and pitchmotionsobtained by a strip theory applied to an upright hull.Secondly,a general method for calculating intersections between ship and waves is presented base on transform of three coordinate systems and the instantaneous area of wet sections is calculated and then the nonlinear Froude-Krylov componentof restoring variation is calculated by integratingwave pressure up to wave surface.Thirdly,radiation and diffraction components are taken into account by using radiation and diffraction force actingon a heeled hull.And then a mathematical model for parametric rolling is developed based on the calculation of restoring variation.Finally,restoringmomentsand parametric rollingof a container ship in regularwave are studied and roll restoring variation isan essential fact for parametric rolling prediction.

Key words:restoringmoment;parametric rolling;Froude-Krylov;waves;ship

參數橫搖是波浪中船舶三種典型傾覆現象(純穩性喪失、參數橫搖、橫甩)之一,是波浪中船舶復原力變化引起的非線性現象。當橫搖頻率接近遭遇頻率一半時,橫搖會突然加劇,甚至導致船舶傾覆,其具體過程是船體從直立位置傾斜時復原力減少,向直立位置復原時復原力增加,復原力這種周期性變化使橫搖加劇。1998年,巴拿馬型C11級集裝箱船APL CHINA號在北太平洋海域迎浪時遭遇嚴重參數橫搖,橫搖角甚至達40°,損失400個集裝箱,其他貨物幾乎全部受到損壞[1],這次嚴重事故以及隨后的幾次參數橫搖事故促使人們要對IMO的完整穩性規則(intact stability code(IS code))進行重新評估,研究制定新的衡準代替現有的衡準,這個新的衡準中就包括三種典型傾覆現象之一的參數橫搖[2]。2008年7月～2009年3月,SAFEDOR(de-sign,operation and regulation for safety)組織了波浪中參數橫搖數值仿真方法研究,其中荷蘭、意大利、日本等16家研究機構參與了此次國際合作研究[3]。在國內,上海交通大學[4]、708研究所[5]和天津大學[6]等研究機構對參數橫搖也做了一些理論計算和實驗方面的研究。但提高波浪中復原力變化計算精度仍是參數橫搖研究的關鍵點,因為復原力變化的微小差異會導致參數橫搖最大橫搖角明顯不同[7]。考慮波浪中復原力的Froude-Krylov力、輻射力和繞射力三部分,進行時間序列復原力變化計算以及參數橫搖預報,研究復原力變化對參數橫搖的影響。

1 船舶運動坐標系及轉換關系

1.1 三種坐標系

船舶在波浪中復原力的計算及公式推導和坐標系的選取緊密相關,采用下述三種坐標系:①固定坐標系O-ξηζ,原點O位于靜止水面,ζ軸向下為正,用來描述波浪;②運動坐標系G-xyz,以船舶重心G為原點,x軸在中線面內,平行于基面,指向船艏為正,z軸向下為正;③參考坐標系G-x′y′z′,它是以船速V隨船一起運動的坐標系,在描述船舶前后、左右運動時,與靜水面平行,在描述船舶上下運動時,與靜水面垂直,但船舶發生旋轉運動時,本坐標系不隨船舶發生橫傾和縱傾,當船舶處于靜止平衡位置時和G-xyz重合。三種坐標系分別如圖1所示。

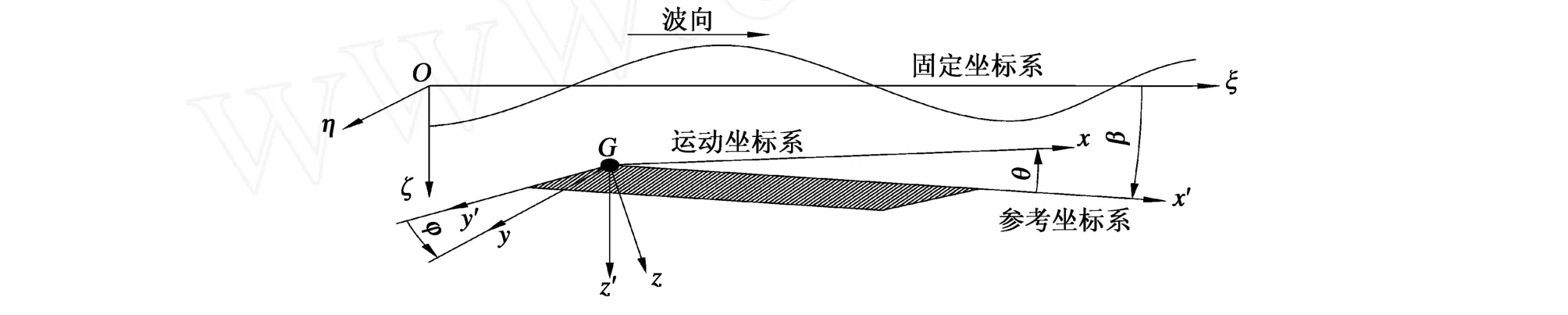
圖1 坐標轉換示意Fig.1 Transform between three coordinate systems

1.2 三個坐標系之間的轉換關系

1)當船舶橫傾φ角度時,參考坐標系G-x′y′z′與運動坐標系G-xyz之間的關系如圖2所示,轉換關系:

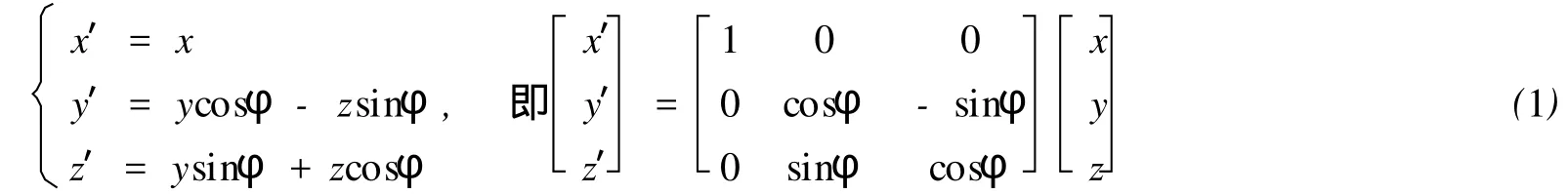
2)當船舶橫傾角為φ,縱傾角為θ,航向角為β時,假設船體重心G此時在固定坐標系O-ξηζ中坐標為ξ=ξG,η=ηG,ζ=ζG,固定坐標系O-ξηζ與運動坐標系G-xyz轉換關系:

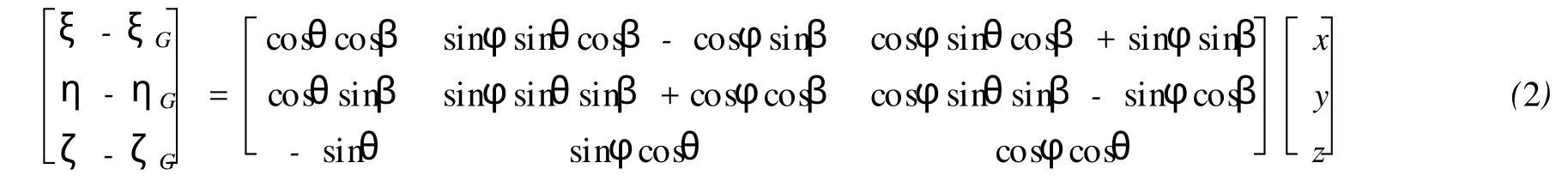
由于船在波浪中航行時縱傾角一般很小,因此,sinθ?θ、cosθ?1,并代入式(2)得:

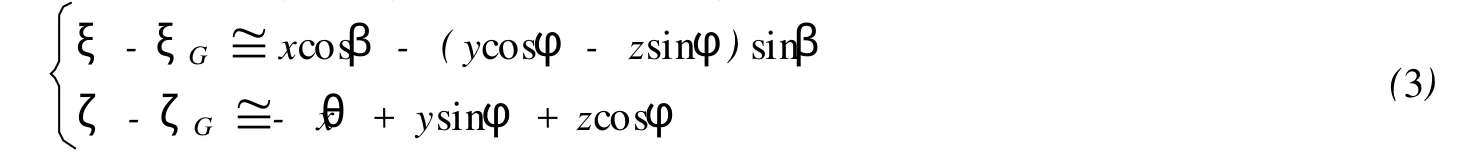
2 船體和波面相對位置的確定

2.1 船舶在規則波中的垂蕩ζG(t)和縱搖θ(t)求解

假設某一規則波振幅為a,波數為k,以波速c在固定坐標系O-ξηζ的ξ方向傳播,t時刻波形表達式:

船舶在規則波中垂蕩和縱搖運動通過下式垂蕩和縱搖的耦合方程求解:

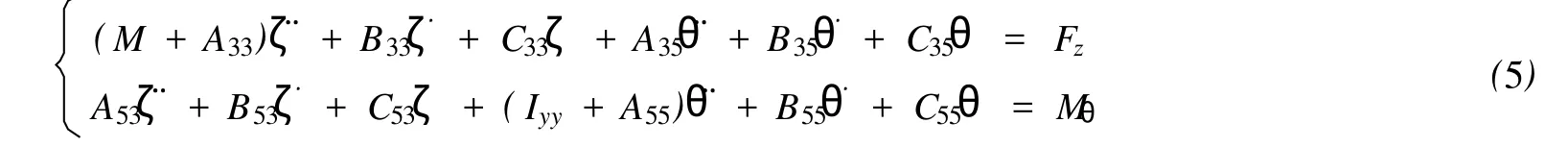
上述Aij是廣義附加質量系數,Bij是廣義阻尼系數。

各系數表達式[8]:

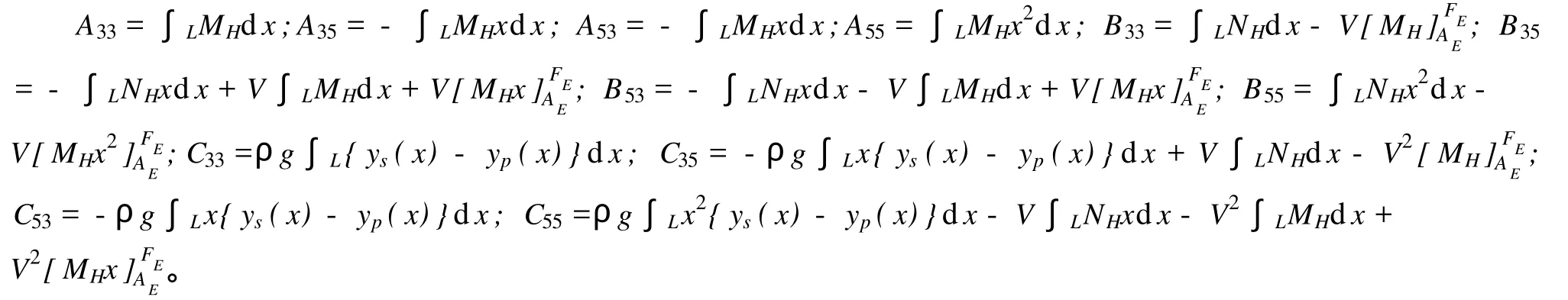
其中,ρ為流體密度,V為船速,L為船長,(AE,FE)為船尾和船首的x坐標,MH、NH為船體斷面垂蕩附加質量及衰減系數,(ys,yp)為船波交點處的y坐標。

上述垂蕩和縱搖的耦合方程求解還需求得波浪強制力Fz、Mθ,其表達式[9]:

利用OSM(ordinary strip method)求解波浪強制力和水動力系數,其中二維水動力系數利用日本船舶技術研究所的菅、原口[10]編寫的程序計算得到。

規則波中時間序列的垂蕩ζG(t)和縱搖θ(t):

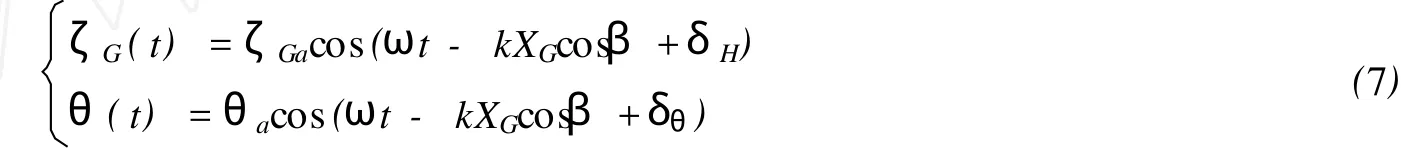
式中:ζGa,θa分別是垂蕩、縱搖振幅,δH,δθ分別是垂蕩、縱搖初始相位,XG是船舶重心在固定坐標系中前進的距離。

2.2 規則波中船舶左右舷與波面的瞬時交點求解

t時刻,在固定坐標系O-ξηζ下,設船體各橫剖面各點處的波高為ζw(i,j,t),船體各橫剖面各點ζ坐標為ζship(i,j,t),船體各橫剖面各點與水面的垂直距離為D(i,j,t),則:

如圖3所示,船-波交點(yp,zp),(ys,zs),也就是與水面的垂直距離D(i,j,t)為零的點。

首先給船體各個橫剖面的各個型值點進行編號,如圖4(c)所示,并求出t時刻各型值點在固定坐標系O-ξηζ下的ζ坐標,即ζship(i,j,t)。由于船-波交點(yp,zp),(ys,zs)與水面的垂直距離為零,則交點相鄰前后兩個型值點相對水面的垂直坐標必一正一負,從而可以在求得船-波一組或多組交點相鄰的前后型值點后,利用線性插值便可求出船-波交點(yp1,zp1),(ys1,zs1),(yp2,zp2),(ys2,zs2),……,然后可計算出各浸水橫剖面面積A(x)及其面積心(yB(x),zB(x))。

3 波浪中復原力計算

3.1 規則波中復原力之Froude-Krylov部分的計算

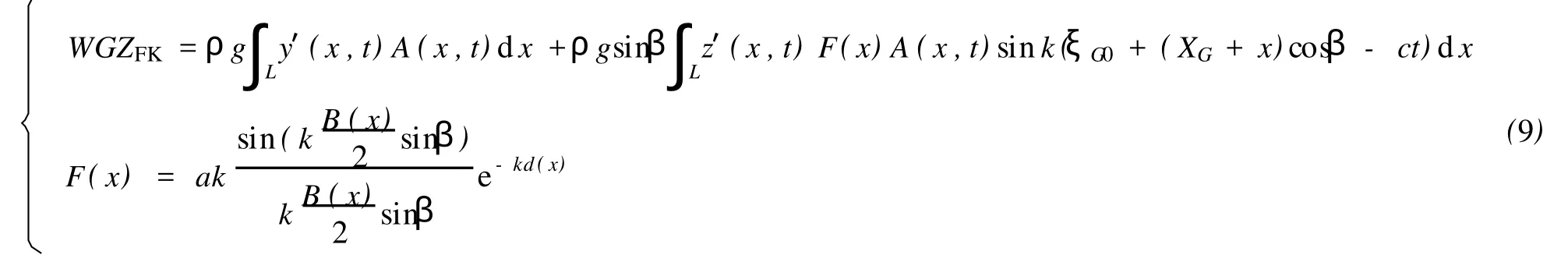
式中:F(x)為各橫剖面的壓力梯度系數;B(x)取船舶靜水中直立狀態時各橫剖面的水線寬;d(x)取船舶靜水中直立狀態時各橫剖面的吃水;A(x,t)為各橫剖面的浸水剖面面積;ξG0船舯在固定坐標系O-ξηζ的初始位置;y′(x,t),z′(x,t)為浸水橫剖面面積心在參考坐標系下的坐標,可根據式(1)求得。由式(9)沿船長積分得規則波中船舶的復原力臂。

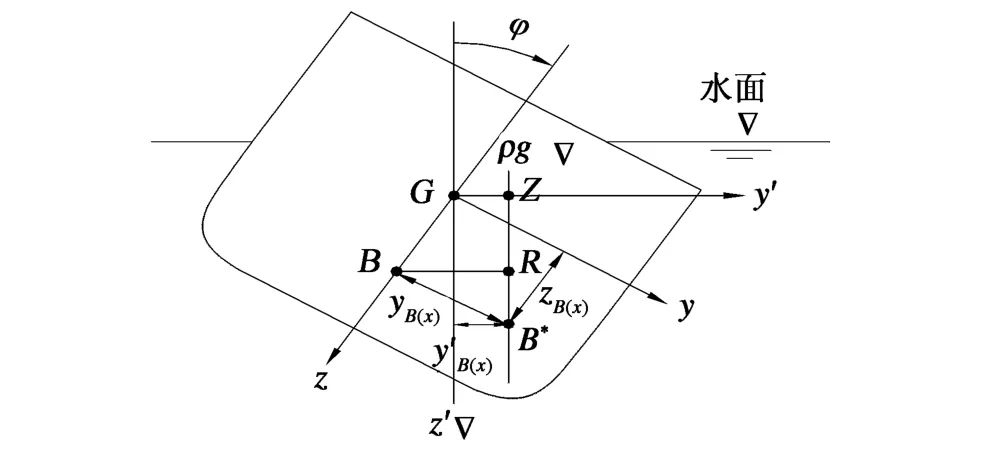
圖2 兩種坐標系下重心和浮心相互位置示意Fig.2 Center of gravity and center of buoyancy in heeled condition

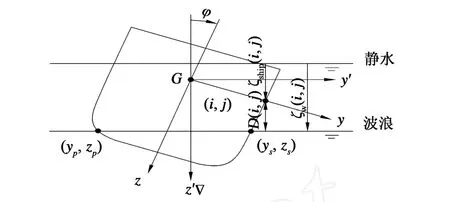
圖3 船波交點求解示意Fig.3 Solving the intersection between ship section and wave

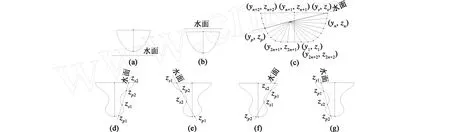
圖4 船波各種交點情況示意Fig.4 Casesof intersection between ship sections and wave

3.2 規則波中復原力之輻射力和繞射力部分的計算

波浪中橫蕩方向輻射力和繞射力以及橫搖方向輻射力矩和繞射力矩公式:

式中:W是排水量,KG是船舶基線到重心的距離,MXa是復原力之輻射力和繞射力部分的變化振幅,δMX是復

原力之輻射力和繞射力部分的變化的初始相位。

在計算復原力之輻射力和繞射力部分時船舶橫傾角度是10°,且和波高成線性關系,動態的復原力之輻射力和繞射力部分看作與橫傾角成線性關系。

波浪中復原力臂:

4 參數橫搖計算

為預報迎浪中參數橫搖,文獻[13]提出了幾種參數橫搖模型,其中梅田等[12]和Hashimoto等[7]拓展了一個簡單的時域參數橫搖預報模型,采用了與文獻[7,12]相同的數學模型,這個模型盡管是針對一個自由度的,但其計算復原力時,考慮了垂蕩和縱搖的耦合運動。

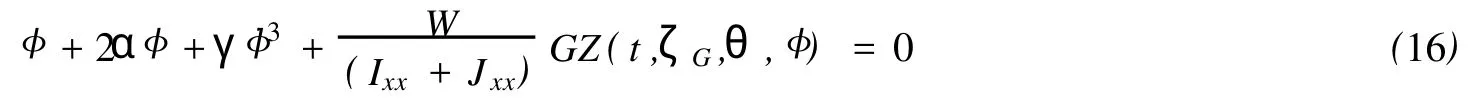
式中:φ為橫搖角,α為線性阻尼系數,γ為非線性阻尼系數,Ixx為橫搖慣性矩,Jxx為橫搖附加慣性矩。α和γ由船模自由橫搖衰減曲線得出。

5 計算實例

以ITTC A1集裝箱船為例計算其在波浪中復原力變化及參數橫搖,該船型的主要參數和型線如表1和圖5～7所示。

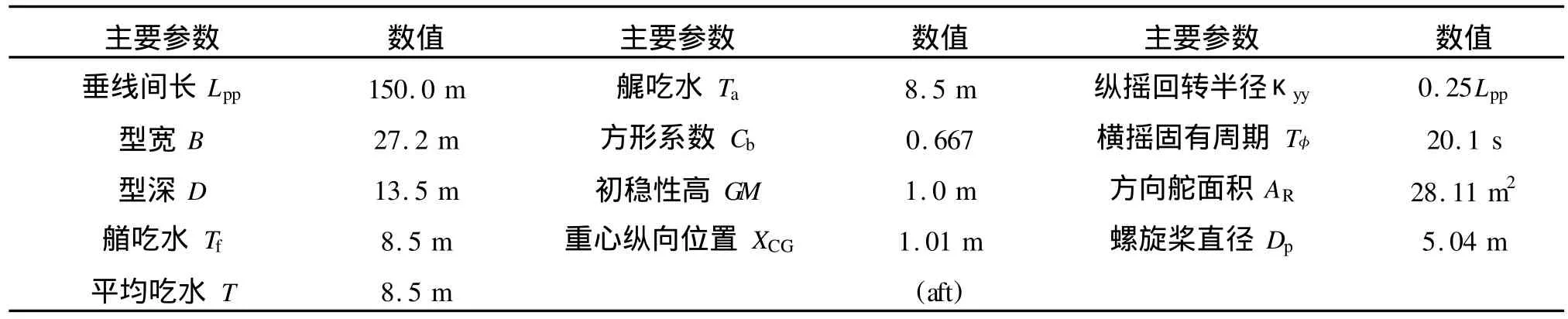
表1 A1集裝箱船主要參數Tab.1 Principal particulars of A1 containership

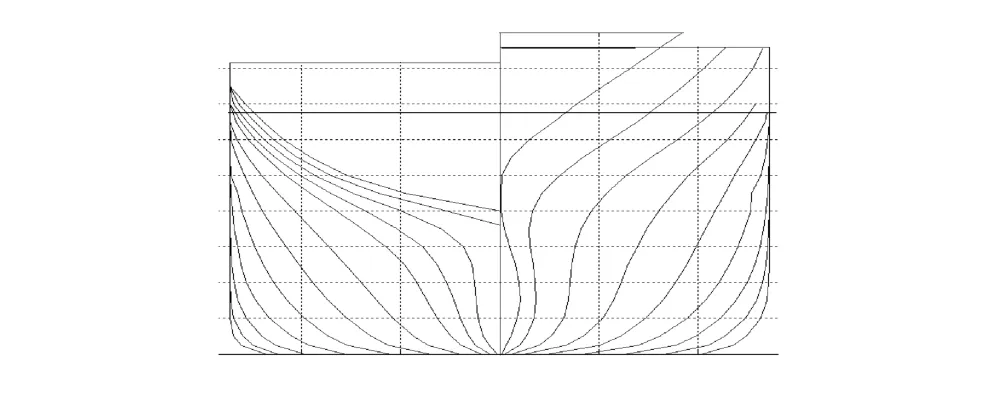
圖5 A1集裝箱船型線Fig.5 Linesof A1 container ship

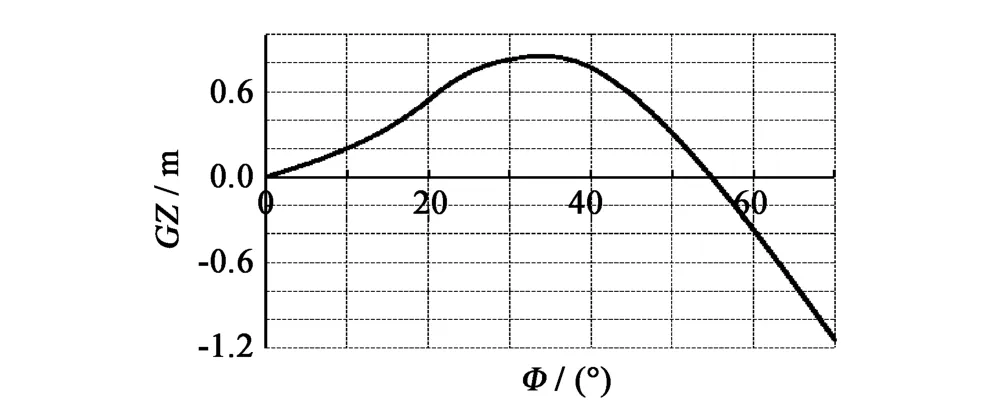
圖6 靜水中復原力臂曲線Fig.6GZcurve in stillwater

從圖8～10可以看出,迎浪中波陡較小時,初穩性高平均值變化和一階初穩性高振幅變化隨著波陡增加而增加,當波陡較大時,航速的不同而出現不同的變化趨勢。

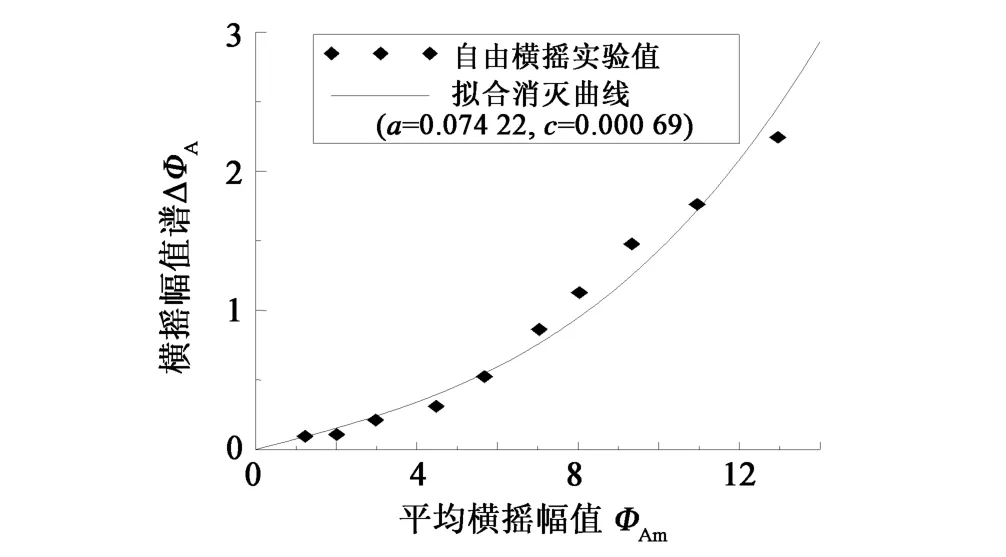
圖7 橫搖消滅曲線Fig.7 Extinction curve(a,care lineart and cubic extinction coefficients)

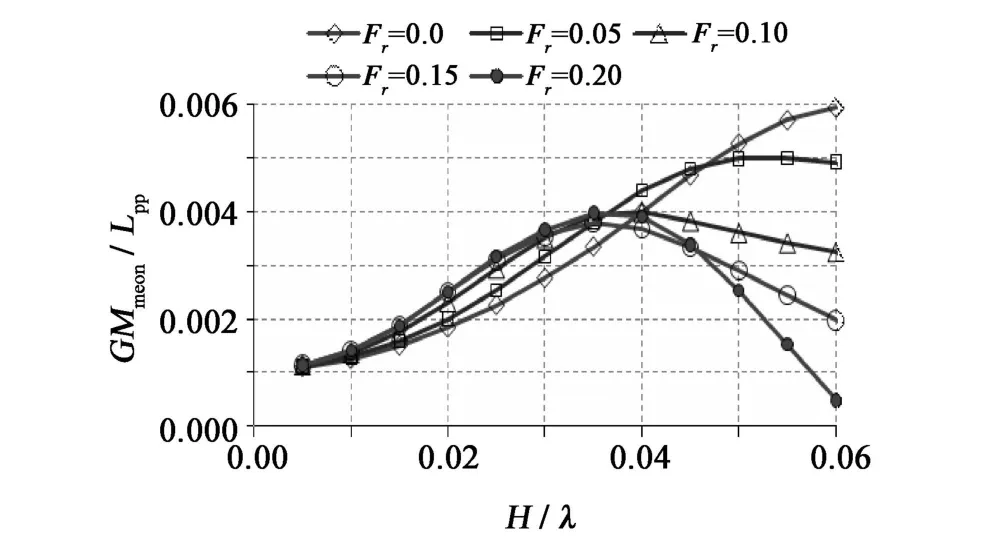
圖8 初穩性高平均值變化Fig.8 Mean of metacentric height variaion withλ/Lpp=1.0,β=180°

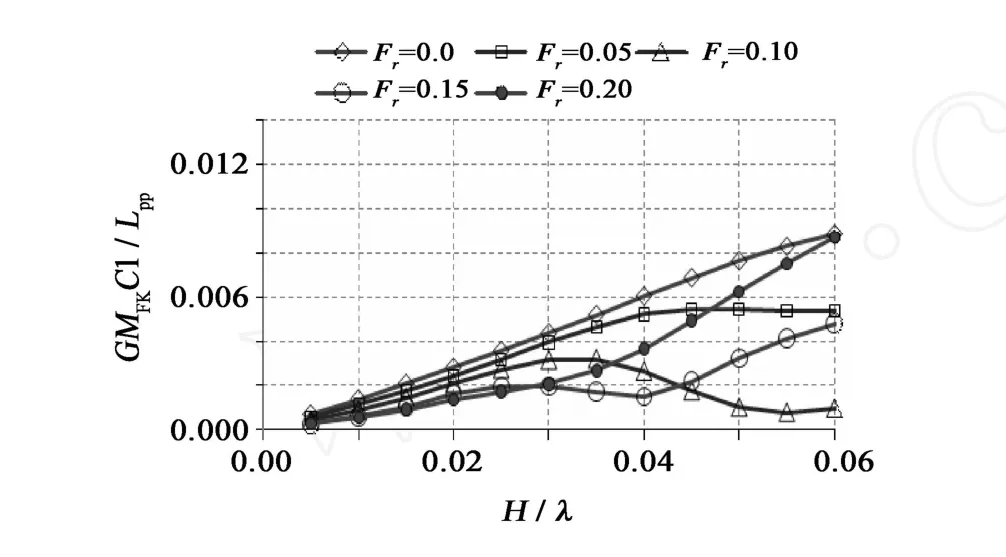
圖9 只考慮Froude-Krylov部分時的一階初穩性高振幅變化Fig.9 Considering part of Froude-Krylov amplitude of harmonic metacentric heightwithλ/Lpp=1.0,β=180°

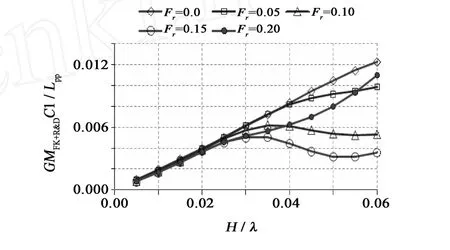
圖10 考慮Froude-Krylov部分、輻射力和繞射力部分時的一階初穩性高振幅變化Fig.10 Considering partsof Froude-Krylov,radiation and diffraction amplitudewithλ/Lpp=1.0,β=180°

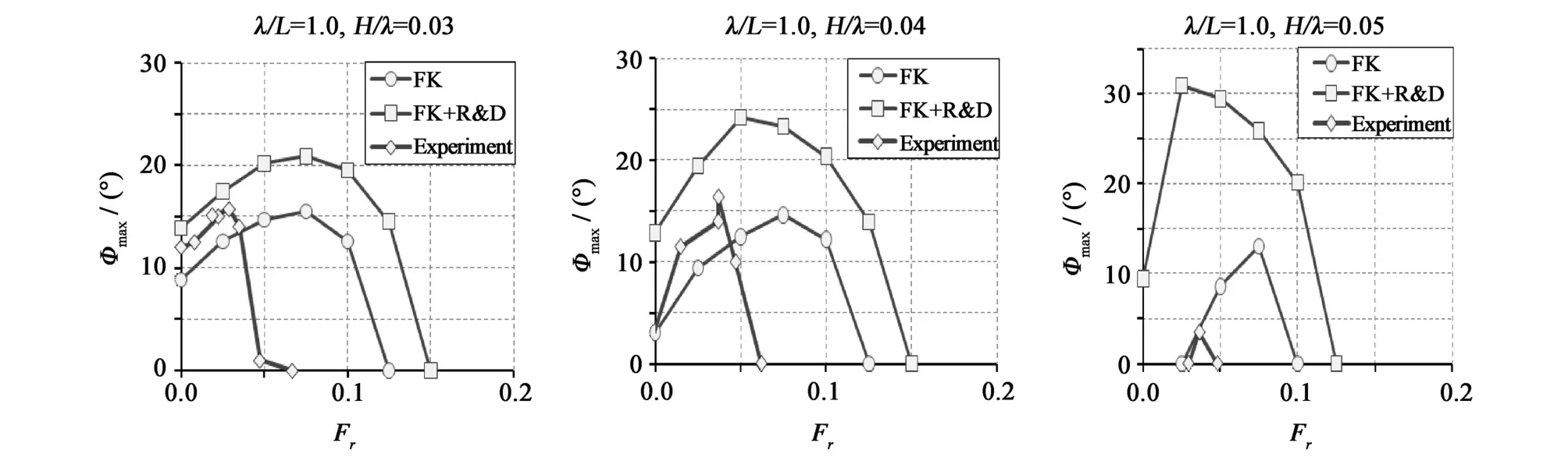
圖11 試驗和模擬計算的最大參數橫搖角比較Fig.11 Comparison in themaximum roll angle between experiment and simulationswithβ=180°

迎浪中同時考慮Froude-Krylov力、繞射力和輻射力影響的初穩性高振幅變化大于只考慮Froude-Krylov力的初穩性高振幅變化,這也是圖11中出現前者橫搖角和航速范圍大于后者的原因。傅汝德數Fr=0.0、0.05時,初穩性高振幅變化隨波陡增加而增加,但H/λ=0.05時參數橫搖角卻變小,其原因是此時初穩性高平均值變大。Fr=0.2時,初穩性高振幅變化隨波陡增加而增加,初穩性高平均值在大波陡時變得很小,但卻沒發生參數橫搖,其原因應該是此時遭遇頻率已跳出發生參數橫搖的頻率范圍。圖11中出現參數橫搖隨波陡增加而消失的現象,其原因就是穩性平均值增加和初穩性高振幅變小。波浪中初穩性高變化,即復原力變化是影響參數橫搖的一個重要因素。復原力變化的微小差異會導致參數橫搖發生的臨界值以及最大參數橫搖角的很大差異,復原力計算應該考慮繞射力和輻射力部分。此算例中只考慮Froude-Krylov部分的參數預報更接近試驗,文獻[12-13]中考慮繞射力和輻射力部分的參數橫搖預報更接近試驗,其采用的是巴拿馬集裝箱船型,繞射力和輻射力部分對參數橫搖預報的影響是否受船型影響有待進一步研究;此外動態的復原力之輻射力和繞射力部分看作與橫傾角成線性關系,在大角度橫搖時,此關系并不成立,這可能是考慮繞射力和輻射力部分時預報偏大的原因之一,有待進一步研究改進,根據橫搖角實時計算動態復原力之輻射力和繞射力部分。數值計算時沒有考慮船速對橫搖阻尼的影響,這可能是數值模擬和試驗差別較大的另一個原因,有待試驗測出有航速時的橫搖阻尼系數,再進一步驗證。假定復原力之輻射力和繞射力部分和波高成線性關系,復原力之輻射力和繞射力部分的變化隨波高增大而變大,這可能是導致波高較大時考慮繞射力和輻射力部分的參數橫搖預報值較大的原因之一。從圖11可以看出,數值模擬能夠評估參數橫搖發生的區域以及預報最大橫搖角。

6 結 語

1)數值模擬能夠評估參數橫搖發生的區域以及預報最大橫搖角,復原力平均值和振幅變化是影響參數橫搖的一個關鍵因素,進一步提高參數橫搖預報精度需提高復原力變化計算的精度,同時應把根據橫搖角實時計算的動態復原力之輻射力和繞射力部分考慮進去。

2)船-波相對位置直接影響復原力計算的準確性,為提高復原力計算的精確性,首先要保證垂蕩和縱搖計算的準確。為進一步提高評估復原力變化的精確性,還要計及縱蕩對船-波相對位置的影響,在計算縱蕩時應考慮波浪增阻對其影響。

3)波高超過某個臨界值后參數橫搖才會發生,但波高變大時會有參數橫搖消失的現象發生。

實際海況多為不規則波,為研究實際海況中參數橫搖現象,下一步將開展群波和長峰不規則波中參數橫搖預報研究。

志謝:本研究工作得到日本大阪大學Prof.N.Umeda的指導,并提供實驗數據,在此表示真摯感謝。

[1] FranceW L,LevadouM,Treakle TW,etal.An investigationof head-sea parametric rolling and its influenceon container lashing systems[J].Marine Technology,2003,40(1):1-19.

[2] Hashimoto H,Umeda N,et al.Predictionmethods for parametric rollingwith forward velocity and their validation[M].Final Reportof SCAPECommittee(part2),2008.

[3] SpanosD,Papanikolaou A.Benchmark study on numerical simulationmethods for the prediction of parametric rollof ships inwaves[C]∥10th Inter.Conf.on Stability of Ships and Ocean Vehicles.2009.

[4] Fan J,Gu X,Miao G,et al.Parametric rollingof a ship in Longitudinal Seas under random waves[C]∥6th Osaka Colloquium on Seakeeping and Stability of Ships.2008.

[5] Yang S,Fan S,Nie J,etal.Experiment and numerical investigationon parametric rolling in regular headwaves for large containership[C]∥6th Osaka Colloquium on Seakeeping and Stability of Ships.2008.

[6] 唐友剛,李紅霞,鄺艷香.船舶參數激勵非線性隨機橫搖運動分析[J].中國造船,2008,49(4):12-18.

[7] Hashimoto H,Umeda N,Sakamoto G.Head-sea parametric rolling of a car carrier[C]∥Proceedingsof the 9th International Ship Stability Workshop.2007.

[11] Lee M C,Kim K H.Predictionofmotion of ships in damaged condition inwaves[C]∥Second International Conferenceon Stability of Ships and Ocean Vehicles.1982:13-26.

[12] 梅田直哉,橋本博公,坂本玄太,等.波浪中で復原力變動推定に關お研究[C]∥關西造船協會春季講演會.2005,24:17-19.

[13] Umeda N,Hashimoto H,et al.Comparison study on numerical prediction techniques for parametric roll[C]∥27th Symposium on Naval Hydrodynamics.2008.

Research on roll restoring variation and parametric rolling in waves

LU Jiang,MA Kun,HUANGWu-gang
(School of Naval Architecture Engineering,State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116024,China)

U661.22

A

1005-9865(2011)01-0061-07

2010-03-22

中國留學基金資助項目(2008606031)

魯 江(1980-),男,山東人,博士生,從事船舶波浪穩性和參數橫搖研究。E-mail:lujiang1980@yahoo.com.cn

對入射波壓力沿船體濕表面進行積分可得復原力之Froude-Krylov部分GZFK,其采用下面公式計算: