深部洞室圍巖分區破裂化的沖擊破壞機制研究

陳建功 ，周陶陶 ，張永興

（1. 重慶大學 土木工程學院，重慶 400045；2. 重慶大學 山地城鎮建設與新技術教育部重點實驗室，重慶 400045）

1 引 言

分區破裂化是指在深部巖體工程中開挖洞室或坑道時，會在圍巖中產生交替的破裂區和非破裂區的現象[1]。20世紀70年代 Adams和Jager在南非Witwatersrand金礦2 000～3 000 m深處采場采用鉆孔潛望鏡觀測到頂板間隔破裂現象，并排除了分區破裂化現象的產生是由于爆破引起的，即不論是在鉆爆法施工的巷道還是采用機械化施工的巷道中，只要條件滿足，巷道圍巖都會產生此現象[2－3]。俄羅斯科學院(原蘇聯科學院)西伯利亞分院Shemyakin等于20世紀80～90年代對分區破裂化現象進行了深部礦井現場試驗研究、實驗室模擬研究、理論分析以及現象的應用研究[4－7]。Курленя和 Опарин[8]在對大量試驗數據的分析和理論研究基礎上，發現各破裂區的半徑服從某種規律，給出了各破裂區的半徑和厚度表達公式，但該公式僅適用于特定礦區。近年來，隨著深部工程的不斷增加，深部一些新的巖石力學現象不斷出現，中國的學者開始關注并開展了深部圍巖特性的研究[9]。在淮南礦區的深部礦井巷道圍巖鉆孔中用鉆孔窺測儀觀察到了分區破裂化效應的存在[10]；通過實驗室模擬試驗也獲得了分區破裂化現象[11－12]；通過數值計算再現了均勻介質巖體中的巷道圍巖分區破裂化現象[13－14]。在這些研究中，有的僅考慮了基于莫爾–庫侖強度理論的剪切滑移破壞，并未得到明顯的分區破裂化效應。

錢七虎院士在國內率先介紹了國外學者關于分區破裂化現象研究的成果，研究了深部巖體工程響應的特征，并且界定了“深部”巖體的范圍[15]，提出深部圍巖分區破裂化現象是一個與空間、時間效應密切相關的科學現象，用傳統的連續介質彈塑性力學不能完全解釋清楚。認為分區破裂化效應的產生，一方面是由于高地應力和開挖卸荷導致圍巖的“劈裂”效應；另一方面是由于圍巖深部高地應力和開挖面應力釋放所形成的應力梯度而產生的能量流。Shemyakin認為，深部巷道圍巖在卸荷條件下裂縫的產生，是在應力集中導致的最大支撐壓力作用處，由于巷道自由面的影響，產生徑向拉伸變形并達到圍巖的極限應變，導致第1個破壞區中裂縫的張開，以及圍巖向著巷道自由面位移的發展導致了“偽掌子面”，即“偽自由表面”的形成，從而引起圍巖再次發生應力重分布。應力重分布將導致第2個“偽自由表面”的形成，從而進一步引起圍巖內應力的重分布。上述過程不斷發展，一直延續到圍巖重分布的應力達不到圍巖的破壞條件為止。這種對分區破裂化機制的解釋僅僅是定性的。本文試圖從應力波波前不連續間斷面角度來探討分區破裂化的形成機制，進而定量確定圍巖中各個破壞區厚度以及半徑關系。

2 分區破裂化的沖擊破壞機制

在高地應力下巖體受到擾動時，其力學性能首先表現為彈性和脆性，然后隨著變形的發展才表現為黏塑性。所以在開挖瞬間，圍巖應力重分布由圍巖的彈性性質決定，首先在圍巖壓力的靜力作用下產生應力重分布，然后因開挖擾動產生的徑向應力波（P波）向圍巖內部傳遞，此波波前就是一個壓力間斷面，其兩側分別是此間斷面位置的靜力解和動力解，因動力解隨時間收斂于靜力解，且其值始終小于靜力解，當此間斷面處的壓力降滿足沖擊波產生的條件時就產生沖擊破壞，在波前徑向壓力降峰值處附近形成一環狀破裂帶，如圖1所示。這也是為什么破壞區巖石很粉碎，不同于其他破壞形式的原因。由于沖擊波以超聲速傳播，其沖擊破壞在瞬間完成，相當于在原來的介質內又形成了一個新的開挖界面，又會重復出現這樣的沖擊破壞區，這種沖擊破壞一直進行到圍巖內由所產生的波前徑向壓力降不滿足沖擊條件時為止。上述斷續的沖擊破壞過程使洞周圍巖內產生交替的破壞及未破壞區域，即分區破裂化現象。

圖1 波前徑向應力分布Fig.1 Distribution of radial stress at wave front

3 球形洞室開挖的徑向應力分析

對于無限介質中一半徑為r0的球形洞室，假設巖體處于靜水壓力p0狀態，其開挖問題可分為兩個分問題的疊加，一是在無窮遠處作用有原巖應力p0，在洞室內壁上作用有一個均布壓力p0，即由原巖應力所引起的應力和位移；二是無原巖應力的作用，在開挖瞬間t=0時刻，在洞室內壁上突然作用一均布拉力p(t)所產生的應力和應變。兩者之和為開挖瞬間圍巖介質的應力場和位移場，見圖 2。第1個問題比較容易解答，問題2歸結為在球形腔內壁上突然作用一均布拉力p(t)所引起的瞬態動力學問題。

問題1的彈性力學解：

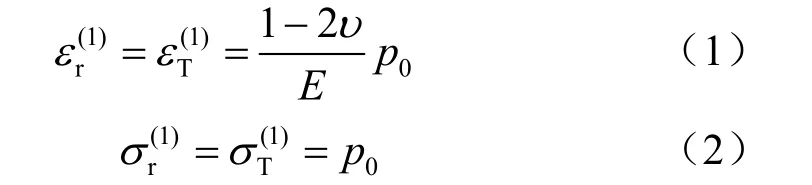
問題2歸結為在洞室內壁上突然作用一均布拉力p(t)所引起的瞬態動力學問題。

式中：H(t)為Heaviside單位階躍函數，滿足：

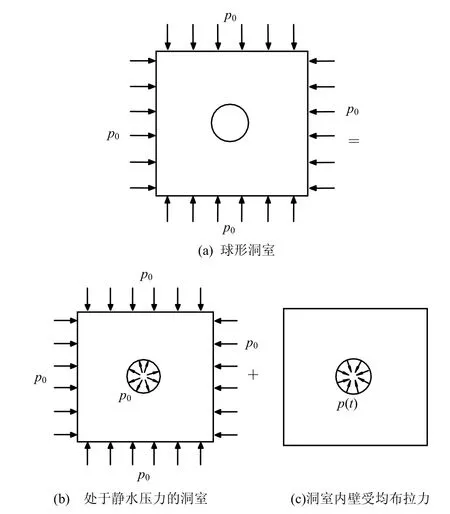
圖2 球形巷道開挖過程的力學模型分解Fig.2 Two parts from mechanical model of spheric tunnel during excavation process

在球對稱拉力p(t)的作用下圍巖介質產生具有球對稱性的無旋波，而不會產生彌散波，也就是只有p波，不產生s波，設位移函數為φ，應滿足波動方程：

式中：cd為縱波波速，為拉梅常數，ρ為介質密度；t為時間變量，在球對稱坐標系（r,θ,?）下，上式可簡化為

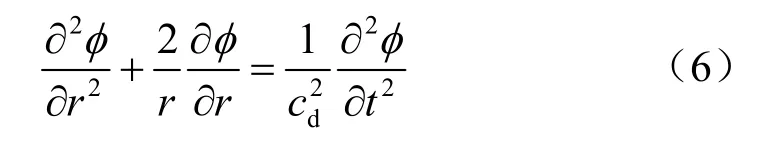
問題相應的邊界及初始條件如下：

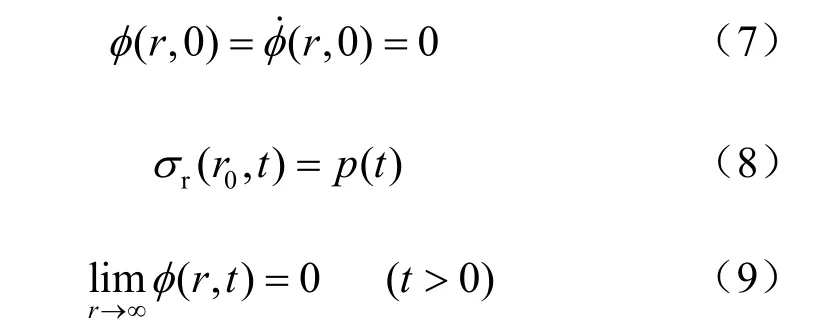
由彈性動力學理論，上述問題的位移勢解為

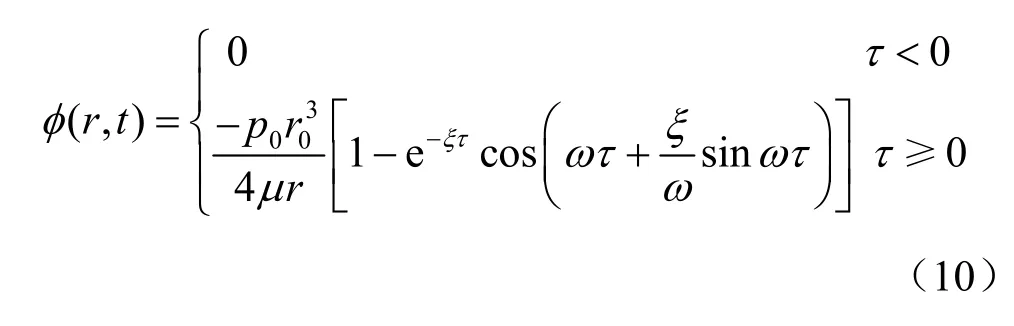
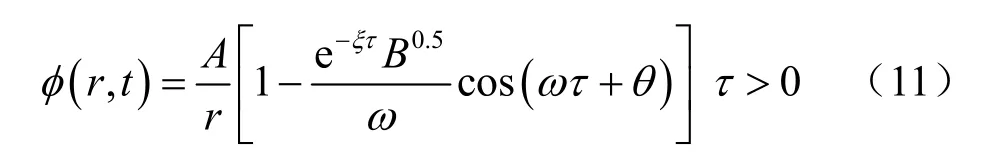
徑向位移為

由彈性理論，應力張量在球坐標中的分量為

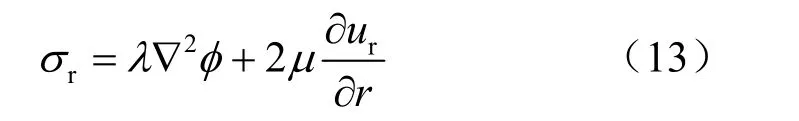
將式（6）、（12）代入式（13）得：

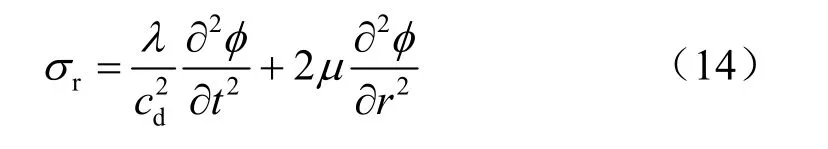
將式（11）代入式（14）得到問題2的徑向應力為

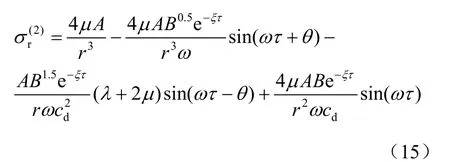
這樣可以得到在空間球對稱下球形洞室開挖的圍巖動態徑向應力場為

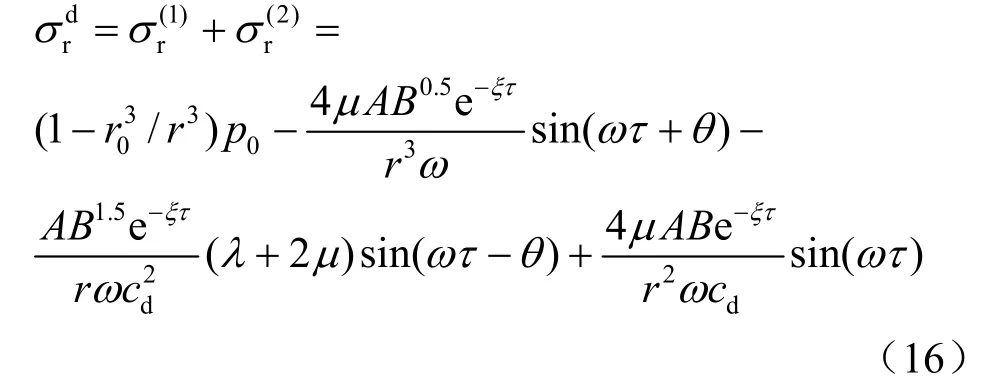
把τ=0代入式（16），得到波前應力為

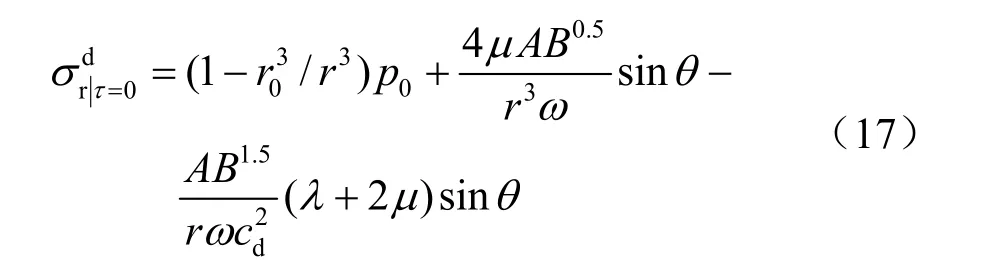
無限大空心球腔內側壓力為 0，外側受均布壓力p0作用下的靜態徑向壓力場為

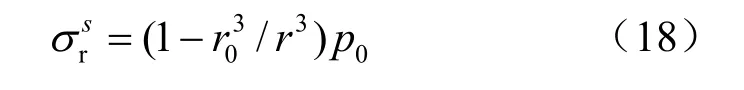
波前應力降：

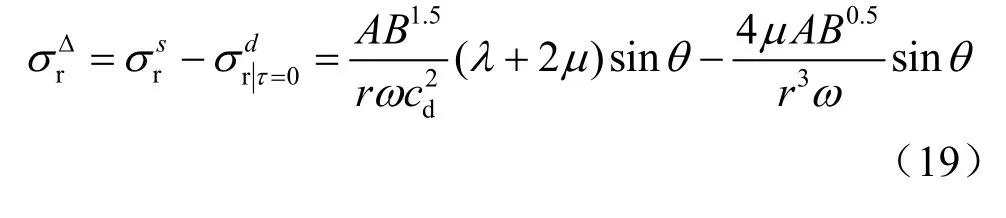
由上一節分析可知，在波前徑向應力降峰值附近會沖擊破壞，破裂區中心半徑位于波前徑向應力降峰值處，由得：

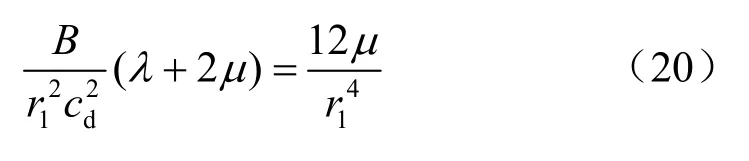
在第1個破裂區產生之前，未擾動圍巖內的靜態徑向應力為：

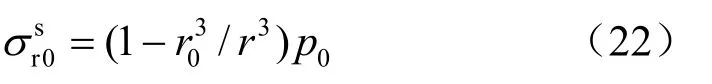
第1個破裂區產生后，形成新的偽開挖面時，由于是沖擊壓縮破壞，沖擊波向開挖面方向傳播，故忽略破裂區圍巖的殘余支撐壓力。此偽開挖面處的卸荷壓力Δp可由下式得到：

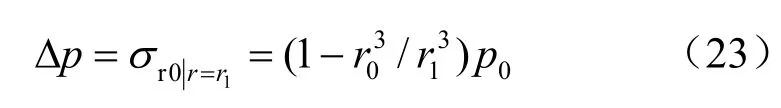
要分析此時的動態徑向應力場，同樣可分成兩個子問題。問題1為第1個破裂區產生之前未擾動圍巖內的靜態徑向應力；問題2為在球形腔內壁上突然作用一均布拉力Δp所引起的動態徑向應力場由式（15）可得：

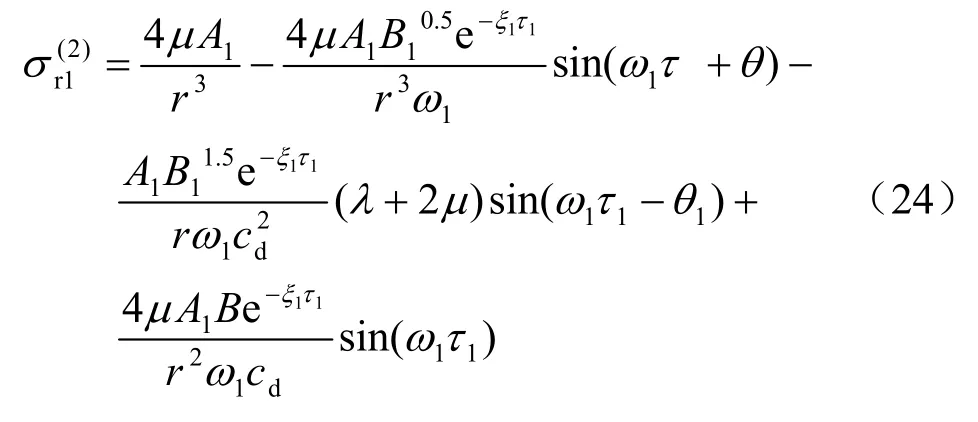
動態徑向應力場為

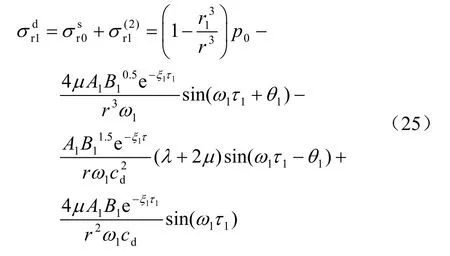
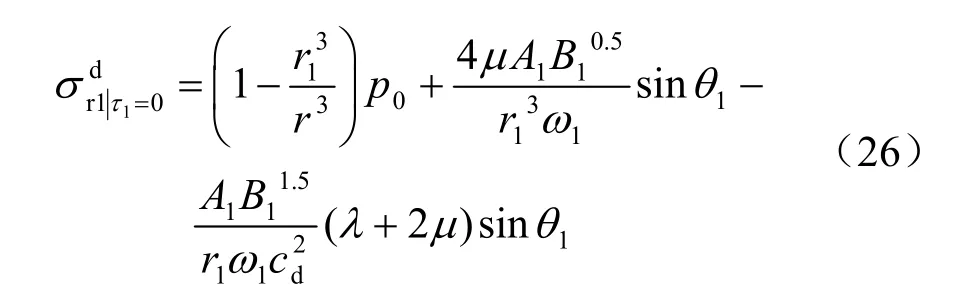
當第1個破裂區產生瞬間，未擾動圍巖內的靜態徑向應力又得到重分布，由下式表示：

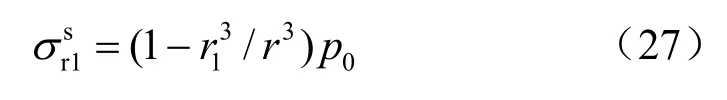
波前應力降為

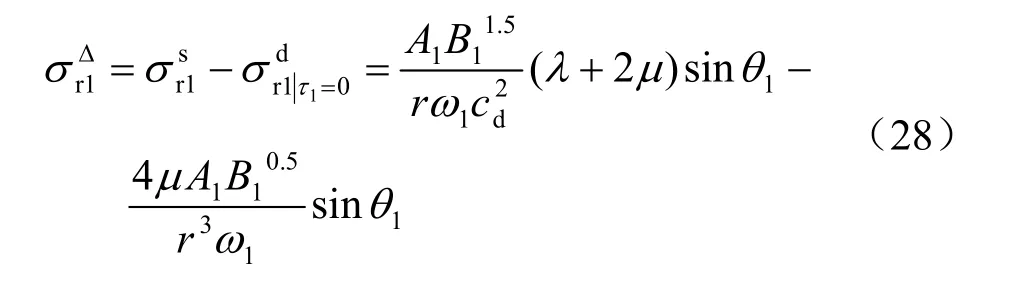
同樣在波前徑向應力降峰值附近會沖擊破壞，破裂區中心半徑r2位于波前徑向應力降峰值處，由得：

由于式（19）和式（28）具有相同的形式，可以得出以下結論：

①發生各次分區破裂化時，波前徑向應力降可以用下面的統一公式計算：

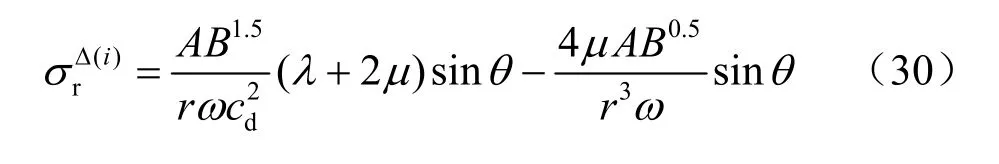
②破裂區半徑只取決于開挖面半徑，同樣，第1個破裂區產生后形成新的偽開挖面時，所產生的第2個破裂區半徑也只取決于第1個破裂區半徑，其比值也為可見球形洞室開挖產生分區破裂化時，巷道半徑及各破裂分區半徑成等比數列，等比值為即：

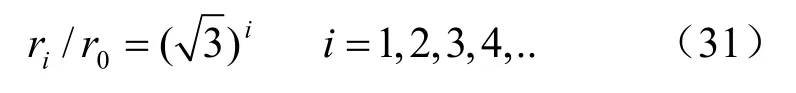
式中：i為破裂區的編號。

比較接近，等比值的不同主要源于本文所采用的球形洞室作為分析模型，而文獻[15]是針對圓形巷道而言。

4 圍巖分區破裂化的沖擊本構方程和破壞準則

早在20世紀60年代，著名巖石力學專家耶格和庫克在他們的經典著作《巖石力學基礎》中提出，應力或應變并不一定是結構破壞的位移原因，Duvall等曾總結了許多研究者的工作，認為質點的振動速度也會使結構產生破壞的原因，其結論是如果質點速度達到0.2m/s時就會發生大的結構破壞，如果質點速度小于0.025 s，則無破壞。根據本文提出的沖擊破壞機制，沖擊破壞的本構模型應結合質點速度、間斷壓力降，由動量守恒定律給出，破壞準則取決于質點速度的限定值。

4.1 沖擊本構方程

波陣面的運動是波動傳播的一種極限形式，在波陣面兩側的運動是不連續的。波陣面前方的質點處于靜止狀態，波陣面后方的質點處于運動狀態，其兩側的一些物理量必定是不連續的，因而波陣面是間斷面。在一級間斷面上，物質的變形梯度和速度是不連續的間斷面即為沖擊波，間斷面上除滿足幾何相容和運動相容條件外，還必須滿足動力相容條件。這里引入動力守恒方程：

式中：a、b為巖石常數，可通過試驗確定，將上式代入式（32）得：

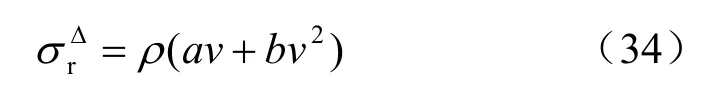
上式即為沖擊荷載下的本構方程。

4.2 沖擊破壞準則

由式（34）可以根據波前壓力降得到沖擊波作用下巖石質點振動速度，當此振速超過某一數值時，即產生沖擊破壞。設一沿x方向以波速為D傳播的沖擊波且函數：

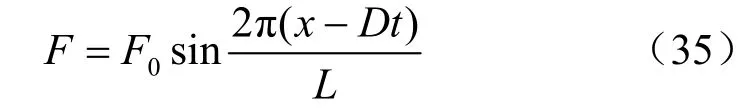
代表此方向的波長為L、振幅為F0的簡諧波，若F為位移，則此波的質點速度為

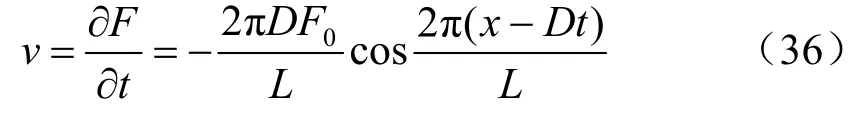
由此引起的應變為

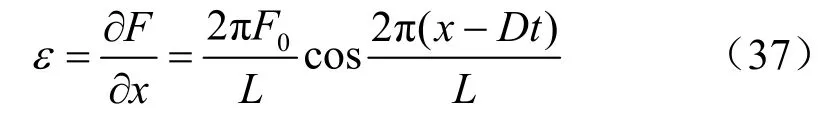
比較式（36）、（37），質點的速度和應變有以下關系：

將式（33）代入式（38）得：

因為沖擊破壞表現為巖石的瞬間壓縮破壞，采用最大壓應變強度準則：

式中：εcr為巖石單軸抗壓強度相對應的極限壓應變。

沖擊荷載下的本構方程式（34）也可表示為

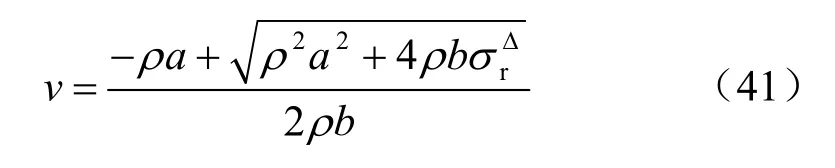
忽略壓應力的負號，由式（39）、（40）、（41）得：

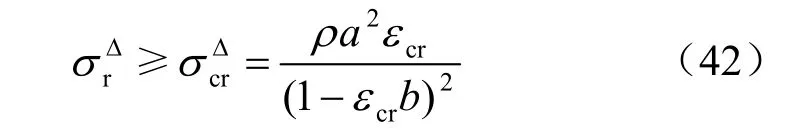
為產生沖擊破壞的臨界壓力降，式（42）即為巖石沖擊破壞準則。

5 算例分析

設球形洞室的半徑為 r0= 2.5 m，圍巖主要為砂質泥巖，原巖應力為p0=35 MPa，彈性模量E=5.25 GPa，密度ρ=2.57 g/cm3，泊松比 υ= 0.276，極限壓應變εcr=1.5×10-3，砂質泥巖巖石常數a= 1 850 m/s 、b=1.60。根據式（16）計算結果得出，圖3動態徑向應力場，圖中徑向拉應力為正，從圖中可以看出，在洞周附近，徑向拉應力急劇下降，遠離洞周時，波前應力衰減速度比較平緩。圖4為波前徑向應力動、靜力曲線和波前壓力降曲線。由圖可知，波前動應力隨半徑的衰減速度比靜應力要快，這樣導致在波前產生壓力降，此壓力降在某一位置有一峰值導致沖擊破壞。

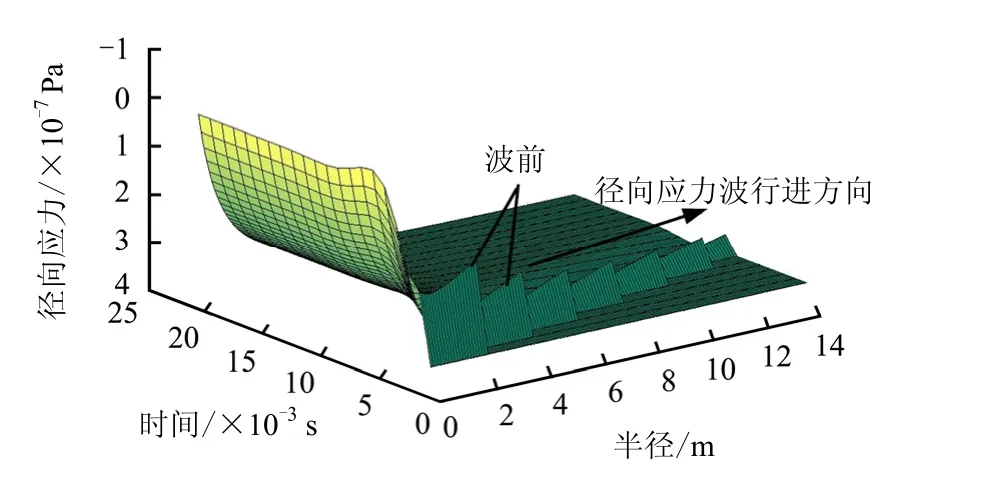
圖3 球形洞室開挖過程的圍巖徑向應力擾動場Fig.3 Disturbed field of radial stress in surround rock during excavation process

波前壓力降曲線與臨界壓力降線相交于兩點，分別為內、外邊界點，兩點之間的區域即為第1破裂區。計算得內邊界點半徑r1i=3.90 m、r1o=4.85 m。

通過計算可以得到另外兩個破裂區的范圍，具體見表1。

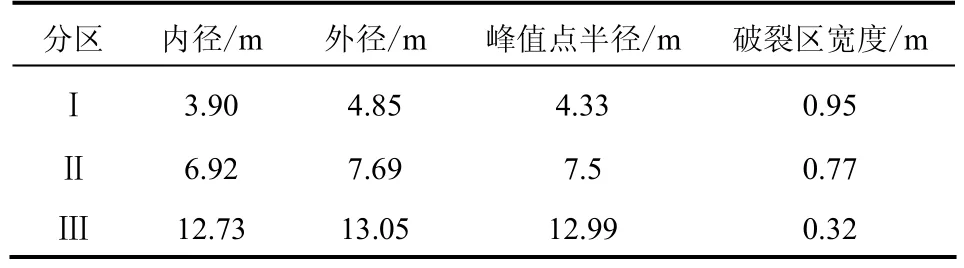
表1 破裂區寬度Table 1 The widths of fractured zones

6 結 論

深部洞室圍巖分區破裂化現象是由于巖體開挖引起的圍巖應力重分布過程中，徑向應力產生了間斷面，當此間斷面壓力差滿足產生沖擊波條件時，即產生沖擊破壞，當此沖擊波衰減很快，其傳播距離無法達到圍巖內壁時，所產生的是局部分區破裂，而不會產生巖爆。當間斷面的條件達不到產生沖擊條件時，圍巖受力變形狀態就屬于淺部圍巖的情況。

（1）推導了洞室開挖瞬間圍巖徑向應力場的動力學理論解，得到了發生各次分區破裂化時，波前徑向應力降的統一計算公式。

（2）根據質點速度、間斷面壓力降，由動量守恒定律推導了圍巖分區破裂化的沖擊本構方程和破壞準則，得到了產生沖擊破壞的間斷面壓力降臨界值計算公式。

（3）在球形洞室及等應力條件下，當產生分區破裂化現象時，各破裂區半徑只取決于開挖面（或偽開挖面）的半徑，且成等比數列，等比值為 3。

[1]錢七虎. 非線性巖石力學的新進展—深部巖體力學的若干問題[C]//中國巖石力學與工程學會編.第八次全國巖石力學與工程學術大會論文集. 北京: 科學出版社,2004: 10－17.

[2]CLOETE D R, JAGER A J. The nature of the fracture zone in gold mines as revealed by diamond core drilling[R]. [S. l.]: Association of Mine Managers, 1972.

[3]ADAMS G R, JAGER A J. Petroscopic observations of rock fracturing ahead of stope faces in deep-level gold mine[J]. Journal of the South African Institute of Mining and Metallurgy, 1980, 80(6): 204－209.

[4]SHEMYAKIN I, FISENKO G L, KURLENYA M V, et al.Zonal disintegration of rocks around underground workings I. Data of in-situ observations[J]. Soviet Mining Science, 1986, 22(3): 157－168.

[5]SHEMYAKIN I, FISENKO G L, KURLENYA M V, et al.Zonal disintegration of rocks around underground workings II. Disintegration of rocks on models of equivalent materials[J]. Soviet Mining Science, 1986,22(4): 223－232.

[6]SHEMYAKIN E I, FISENKO G L, KURLENYA M V,et al. Zonal disintegration of rocks around underground workings III. Theoretical notions[J]. Soviet Mining Science, 1987, 23(1): 1－6.

[7]SHEMYAKIN E I, FISENKO G L, KURLENYA M V,et al. Zonal disintegration of rocks around underground workings IV. Practical applications[J]. Soviet Mining Science, 1988, 24(3): 297－302.

[8]КУРЛЕНЯ М В, ОПАРИНВН. Проблемы нелинейной геомеханики Ч.1[J]. ФТПРПИ, 1999, (3): 12－23.

[9]李德忠, 李冰冰, 檀遠遠. 礦井深部巷道圍巖變形淺析及控制[J]. 巖土力學, 2009, 30(1): 109－112.LI De-zhong, LI Bing-bing, TAN Yuan-yuan. Analysis and control of distortion of surrounding rock of roadway at deep ground of mine[J]. Rock and Soil Mechanics,2009, 30(1): 109－112.

[10]李術才, 王漢鵬, 錢七虎, 等. 深部巷道圍巖分區破裂化現象現場監測研究[J]. 巖石力學與工程學報, 2008,27(8): 1545－1553.LI Shu-cai, WANG Han-peng, QIAN Qi-hu, et al. In-situ monitoring research on zonal disintegration of surrounding rock mass in deep mine roadways[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(8): 1545－1553.

[11]顧金才, 顧雷雨, 陳安敏. 深部開挖洞室圍巖分層斷裂破壞機制模型試驗與分析[J]. 巖石力學與工程學報,2008, 27(3): 433－438.GU Jin-cai, GU Lei-yu, CHEN An-min. Model test study on mechanism of layered fracture within surrounding rock of tunnels in deep stratum[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 433－438.

[12]陳旭光, 張強勇. 高應力深部洞室模型試驗分區破裂現象機制的初步研究. [J]. 巖土力學, 2011, 32(1): 84－90.CHEN Xu-guang, ZHANG Qiang-yong. Mechanism analysis of phenomenon of zonal disintegration in deep tunnel model test under high geostress[J]. Rock and Soil Mechanics, 2011, 32(1): 84－90.

[13]周小平, 錢七虎. 深埋巷道分區破裂化機制[J]. 巖石力學與工程學報, 2007, 26(5): 877－885.ZHOU Xiao-ping, QIAN Qi-hu. Zonal fracturing mechanism in deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 877－885.

[14]唐春安, 張永彬. 巖體間隔破裂機制及演化規律初探[J]. 巖石力學與工程學報, 2008, 27(7): 1362－1369.TANG Chun-an, ZHANG Yong-bin. Discussion on mechanism and evolution laws of fracture in rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(7): 1362－1369.

[15]錢七虎. 深部巖體工程響應的特征科學現象及“深部”的界定[J]. 華東理工學院學報, 2004, 27(1): 1－5.QIAN Qi-hu. The characteristic scientific phenomena of engineering response to deep rock mass and the implication of deepness[J]. Journal of East China Institute of Technology, 2004, 27(1): 1－5.

[16]戴俊. 巖石動力學特性與爆破理論[M]. 北京: 冶金工業出版社, 2002.