飽和土結構性參數演化規律及其簡化模型研究

胡 偉，韓建剛，李光范

（海南大學 土木建筑工程學院，海口 570228）

1 引 言

土的結構性是土顆粒空間排列和粒間聯結作用的力學效應[1－2]。實踐表明：絕大多數天然土體都具有一定的結構性，且這種結構性對土體的工程特性有著很大的影響[3]。土體結構性研究的關鍵是要找到一個合適的定量化指標，建立巖土微結構與宏觀力學效應之間的定量表達關系，發現巖土結構性及其所反映出的宏觀力學效應的變化。文獻[4]建議了根據原狀土、飽和原狀土和重塑土的壓縮試驗，基于壓縮應變來定義和測定土結構性定量參數，把這類結構性參數歸為應變型。文獻[5]中使用的是孔隙比，也應屬于這一類型。文獻[6]中建議對原狀土、飽和原狀土以及相同含水率和干密度的重塑土進行三軸試驗，依據它們的應力-應變曲線，以得到的給定應變條件下不同結構狀態土各自的主應力差定義的綜合結構勢來反映擾動、浸水和加荷作用下的結構性變化。把這類結構性參數歸為應力型，文獻[7]中對動荷載作用下土體結構性參數的定義也屬于這一類型。文獻[8－9]中把非均勻的結構性土體看成由膠結塊和軟弱帶組成的二元介質材料。為了定量的評價受荷中兩者各自所起的作用，引入了剪切抗力分擔率系數，此系數是對不同的試樣達到破壞狀態時軟弱帶所發揮的剪切抗力的比率。顯然這里定義的結構性參數對應于土體的破壞狀態。為了得到結構性參數加載全過程的定量評價，本文以飽和黃土為研究對象，引入兩類超固結比的概念，在對原狀飽和黃土、重塑飽和黃土進行三軸不排水剪切試驗的基礎上，將應力分擔率推廣到任意變形下的情形，定義了結構性發揮系數，并給出了其計算模式及相應的理論計算公式。

2 結構性量化試驗研究

表1 結構性飽和黃土指標Table 1 Property indexes of structural saturated loess

考慮到工程實際，定義兩類超固結比：第1類是前期固結壓力不同，當前固結圍壓相同而形成的第1類超固結狀態β1，如圖1中的A、B點所示。

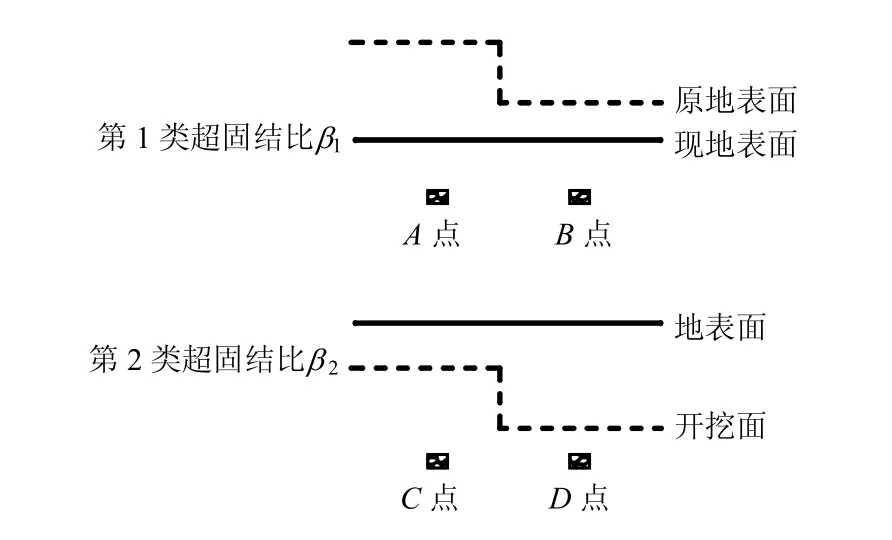
圖1 兩類超固結比定義示意圖Fig.1 Sketch maps of two over-consolidation ratios

此類固結比適用于由于開挖而引起的超固結狀態，當前應力狀態清楚的；第2類是前期固結壓力相同，當前固結圍壓不同而形成的第2類超固結狀態β2，如圖1中的C、D點所示。此類超固結比適用于液化引起的似超固結狀態，前期固結壓力是已知的。

試驗中，第1類超固結比試樣通過加載到不同圍壓，固結后卸載到相同的當前圍壓獲得不同的超固結比β1，如4個試樣分別在50、75、100、200 kPa圍壓下固結后均卸載至50 kPa，得到的第1類超固結比分別為：β1=1、β1=1.5、β1=2.0、β1=4.0；第二類超固結比試樣通過加載到相同圍壓，固結后卸載到不同的當前圍壓獲得不同的超固結比β2，如4個試樣先均在 100 kPa圍壓下固結后分別卸載至100、66.7、50、25 kPa得到的第2類超固結比分別為：β2=1、β2=1.5、β2=2.0、β2=4.0。將對應的飽和原狀黃土和完全重塑飽和黃土三軸剪切試驗所得的應力水平-應變水平曲線繪制在同一 σi- ei坐標下，如圖2所示，其中應力水平σi、應變水平ei分別定義如下：

在圖2所示的 σi-ei關系圖中，對應相同的應變水平ei，飽和原狀黃土對應的應力水平為σis，完全重塑飽和黃土為σir，則定義應力分擔率系數如下：

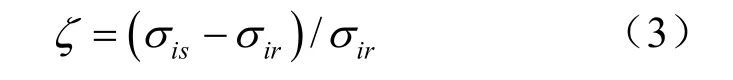
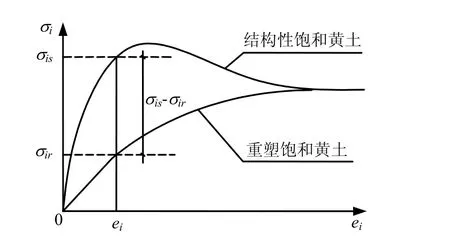
圖2 應力分擔率計算原理Fig.2 The calculation of stress share ratio

ζ表示相同圍壓下不同應變水平時土體結構性在抵抗剪切變形中的貢獻比例，它是應變水平ei的函數，即 ζ= f(ei)。如果針對不同圍壓下進行類似的定義，則可以得到相同應變水平不同圍壓時ζ的變化規律。

圖3中給出了3種圍壓下正常固結試樣的典型ζ- ei曲線。試驗中以應變水平10%為破壞標準，即此時土體的結構性被完全破壞，應力分擔率為 0。從圖中可以看出，應力分擔率隨應變水平的變化曲線明顯分為兩個階段：第1階段幾乎表現為線性增長，也就是此階段結構性是處于線性發揮狀態；當應變達到一定值后，應力分擔率出現峰值，隨后結構性開始發生破壞，進入到第2階段。在此階段內，應力分擔率隨著變形的增長而減小，呈雙曲線變化，變化速率先快后慢，最終趨于 0，土體退化為完全重塑狀態。上述變化規律表明，在很小變形下，結構性強度就能被充分發揮出來，并達到峰值，隨即又被迅速破壞。這也意味著結構性對變形初期土體力學性能的影響是相當顯著的，隨著變形的增大，其影響也越來越小。從圖中還可以看出，固結圍壓越小，應力分擔率的峰值越大。這表明固結壓力對結構性有破壞作用，固結圍壓越小，結構性的影響則相對越大。

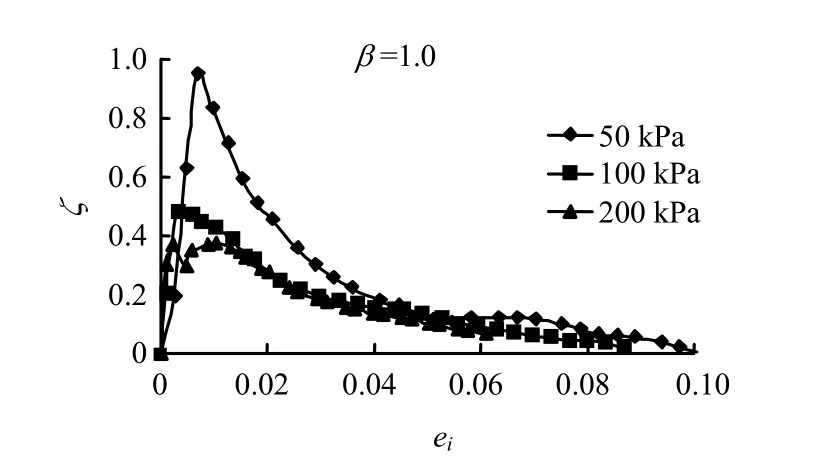
圖3 正常固結土ζ -ei 關系曲線Fig.3 ζ -ei curves of normal consolidated soil

3 結構性演化計算模型

上述定義的應力分擔率系數雖然很好地反映了結構性的演化規律，但在不同情況下這種規律并不具有歸一性，不便于實際應用。對應力分擔率2階段變化特點的進一步分析可知，土體結構性的破壞具有相應的應變閾值，在變形未達到該閾值之前發生卸載的話，土體的結構性是能完全恢復的，在下一次再加載中結構性仍能發揮到其最大值；當變形超過閾值后，土體的結構性就已部分被破壞，在后期的加載中，已無法發揮出其最大值。據此定義結構性發揮系數η如下所示，其中ζmax為應力分擔率峰值。

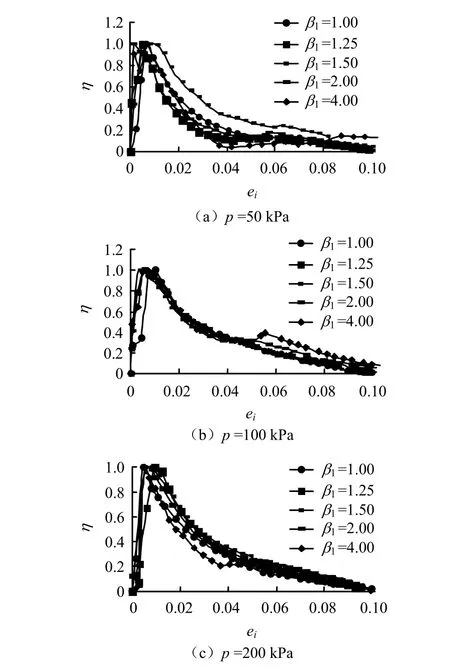
圖4 不同第1類超固結比下η -ei變化規律Fig.4 η -ei curves under different first types of over-consolidated ratios

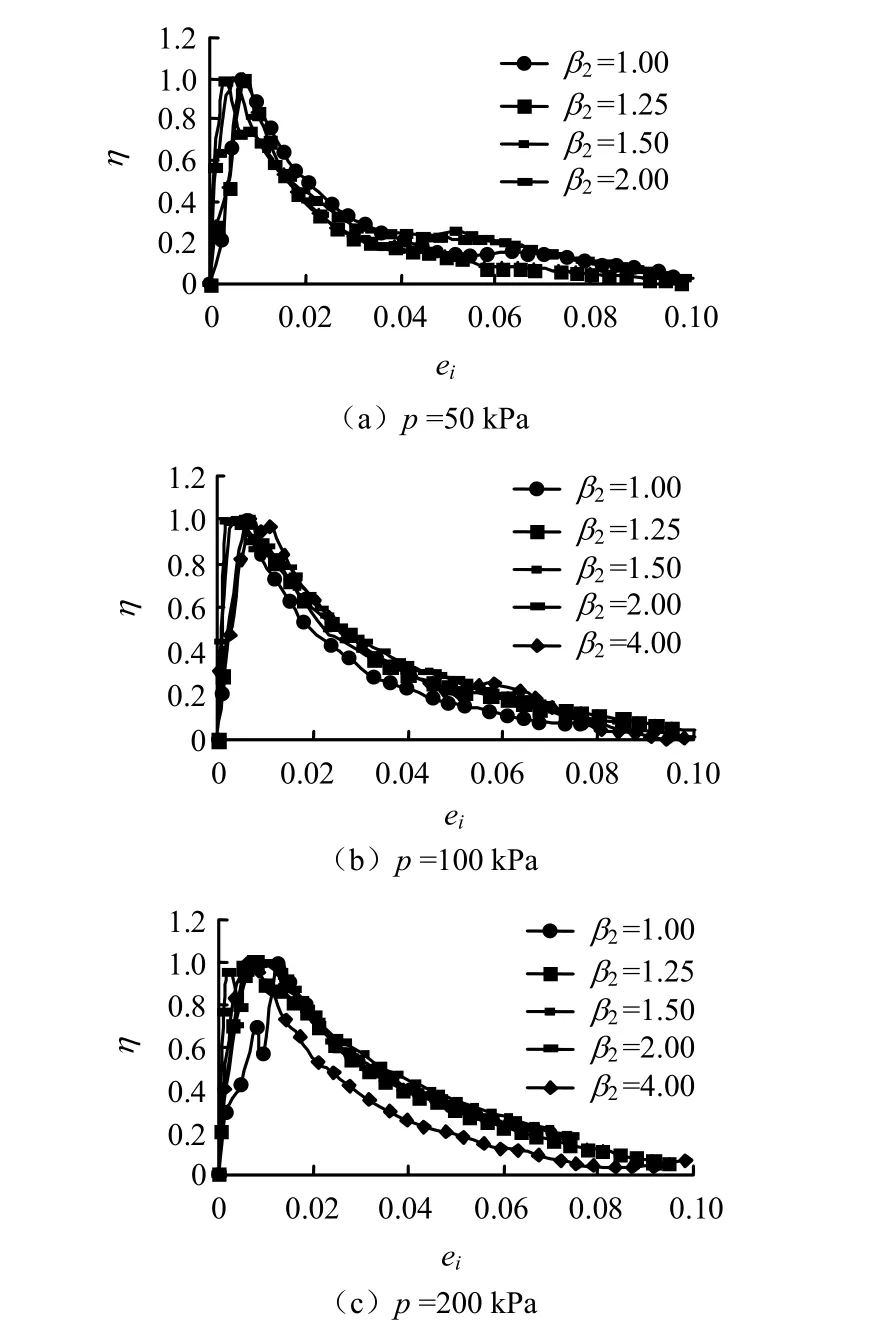
圖5 不同第2類超固結比下η -ei變化規律Fig.5 η -ei curves under different second types of over-consolidated ratios

不同圍壓、兩類超固結比下結構性發揮系數隨變形水平的變化規律如圖4、5所示。從圖中可以看出：結構性發揮系數隨應變水平的變化分為兩段：峰值應變之前，η呈線性增長；峰值之后，則隨著變形的增大呈對數規律減小。上述規律對于不同的圍壓下的不同超固結比，都具有很好的穩定性。圖6為3種圍壓的兩種不同類型超固結比試樣的結構性發揮系數隨變形水平的變化規律。從圖中可以看出，兩類超固結比下，結構性發揮系數的變化規律也具有較好的歸一性，故可以用同一計算模式進行計算。這也意味著當第一類超固結土樣當前圍壓和第2類超固結土樣前期固結壓力相同時，兩者結構性演化規律的的模擬計算中所不同的是應力分擔率的峰值ζmax不一樣，結構性發揮系數計算模式是相同的。

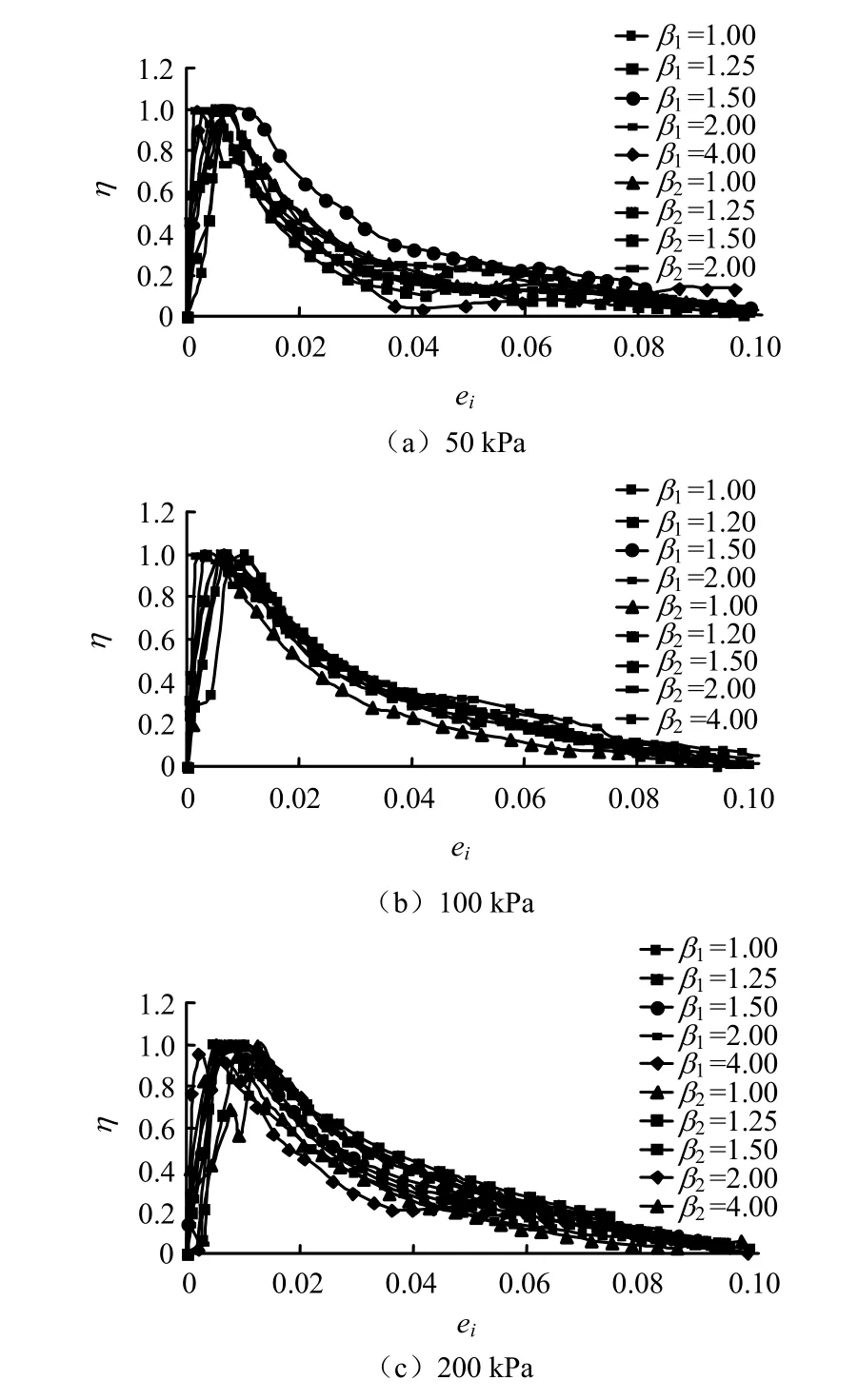
圖6 相同圍壓、兩類超固結比下η -ei變化規律Fig.6 η -ei curves under different two types of over-consolidated ratios

綜合上述分析可知，結構性發揮系數的演化規律可采用如圖7所示的計算模式。

相應的理論式如式（5）所示，其中獨立的參數只有2個，即結構性初始破壞應變閾值ei,sta、結構完全破壞應變值ei,ult，其余3個參數a、b、c均為計算參數。

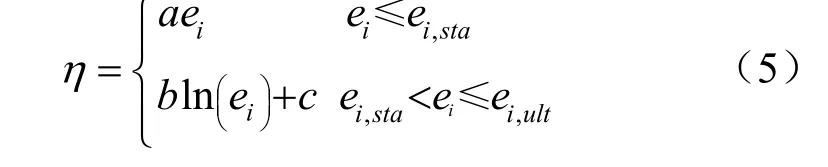
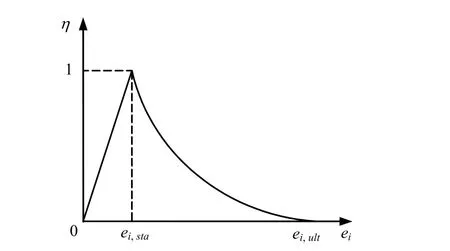
圖7 η 計算模式Fig.7 The calculation model of η

25個試驗結果的統計如圖8所示，離散系數為0.067 7，由此可知，對于給定的土樣，應變閾值ei,sta具有較好的穩定性。本次試驗土樣ei,sta平均值為0.655%，即當 ei＜ 0.655%時，η呈線性增長；此時ηmax= 1；結構性完全破壞時對應的應變水平取ei,ult= 10%，即當 ei≥ 10%時，η=0；當0.655%＜ei＜ 10%時，由一對數曲線來確定。根據邊界條件可以確定出 a=152.7、b=-0.367、c=- 0.845。則任意應變水平下結構性應力分擔率由一個3段式函數確定：

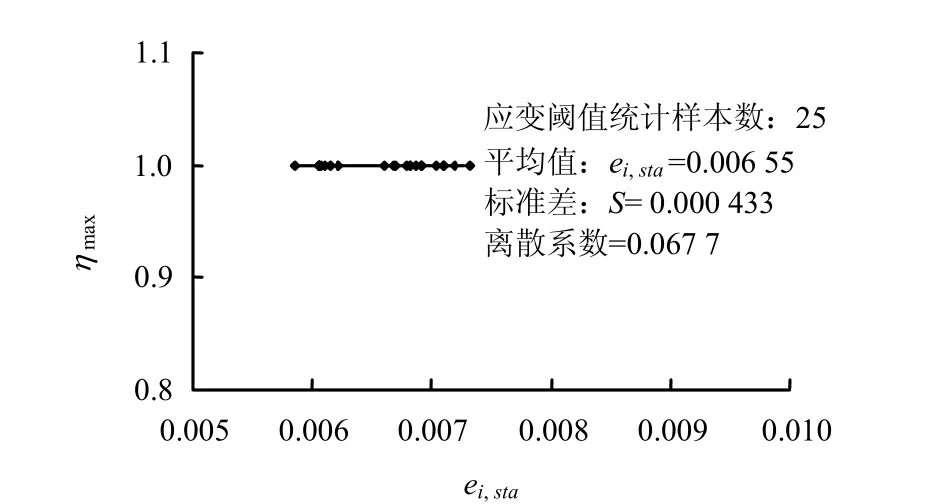
圖8 應變閾值統計Fig.8 The statistics of strain threshold value

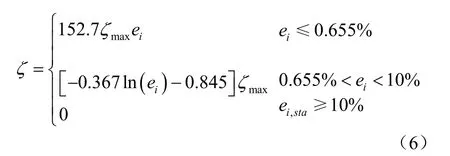
4 計算模型驗證

由式（6）可知，如果土體破壞標準事先確定的話，確定應力分擔率的演化規律也僅需2個參數，即結構性初始破壞應變閥值ei,sta和該應變水平對應的應力分擔率峰值ζmax。應力分擔率一旦確定，若重塑土的應力-應變關系表示為 σi= f(ei)，則結構性土體的應力-應變關系可表示為

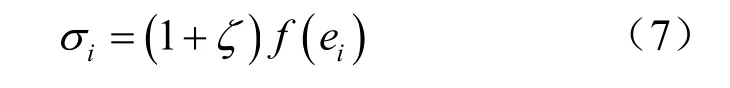
圖9為不同圍壓下(50，100，200 kPa)重塑土、結構性土的應力-應變試驗曲線和公式計算曲線的對比圖。從圖中可以看出，計算和試驗曲線符合得較好，這證明了本文提出的結構性量化計算模式的有效性。

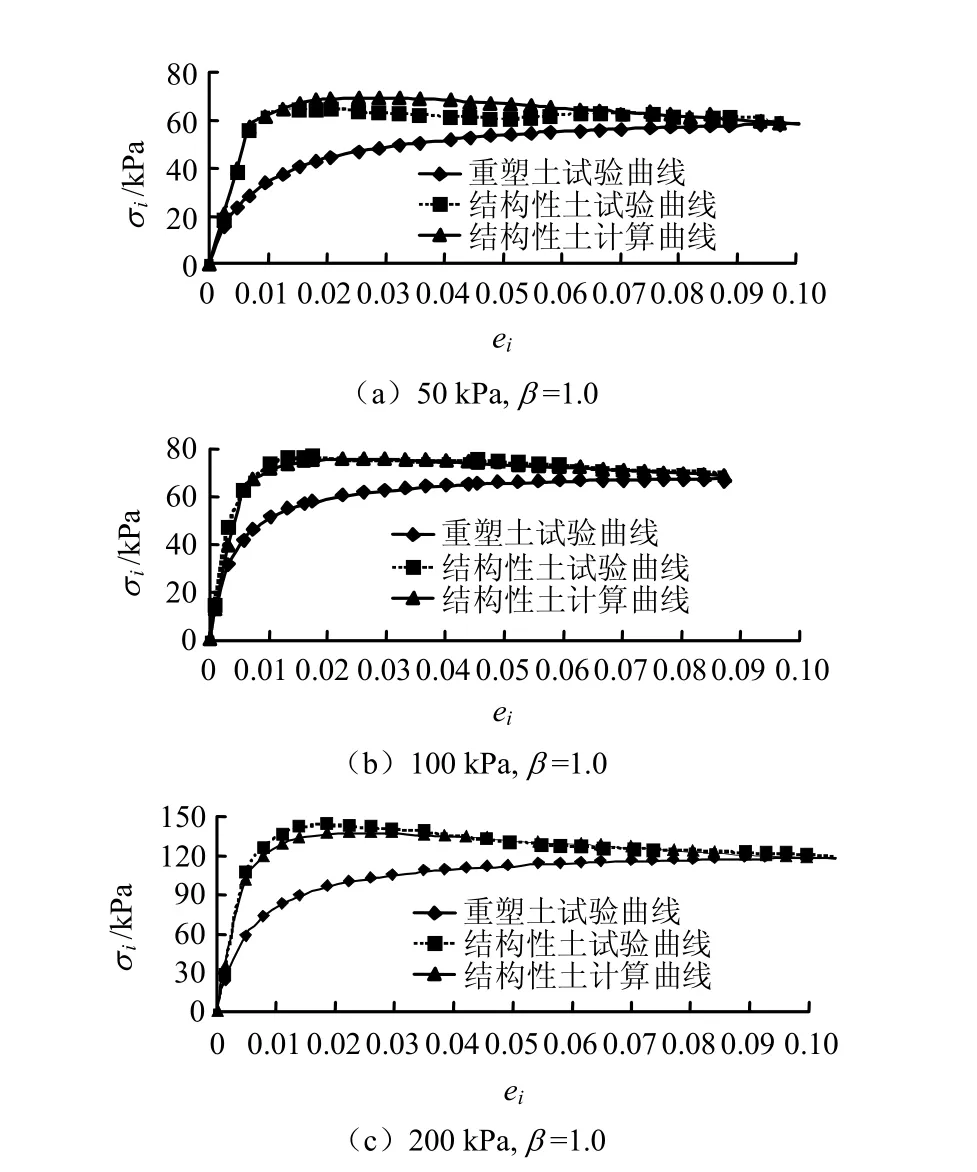
圖9 應力-應變試驗、計算曲線對比Fig.9 Comparison between test’s stress-strain relationships and calculation ones

5 結 語

結合工程實際，本文引入了兩類超固結比的概念，對不同圍壓下的兩類不同超固結比飽和原狀、重塑黃土試樣進行三軸固結不排水剪切試驗。結合應力分擔率的定義對試驗所得的應力-應變曲線進行整理，獲得了應力分擔率隨應變水平呈兩階段特征的變化曲線。進一步引入結構性發揮系數的概念對應力分擔率曲線進行歸一化處理，并由此提出了結構性的計算模式和相應的理論計算公式。理論公式為一個3段式函數，形式簡單、參數少且具有較好的穩定性。對比分析表明：公式計算和試驗結果具有很好的一致性，證明了本文提出的結構性量化計算模式的有效性。

[1]邵生俊, 周飛飛, 龍吉勇. 原狀黃土結構性及其定量化參數研究[J]. 巖土工程學報, 2004, 26(4): 531－536.SHAO Sheng-jun, ZHOU Fei-fei, LONG Ji-yong.Structural properties of loess and its quantitative parameters[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 531－536.

[2]寧樹軍, 張樹光. 土的結構性對路基穩定的影響[J]. 沈陽大學學報, 2002, 14(4): 46－48.NING Shu-jun, ZHANG Shu-guang. Effect of soil’s configuration to roadbed stabilization[J]. Journal of Shenyang University, 2002, 14(4): 46－48.

[3]劉用海, 朱向榮, 吳健, 等. 寧波軟土結構性成因及其對工程特性影響的研究[J]. 工業建筑, 2008, 38(3): 68－71.LIU Yong-hai, ZHU Xiang-rong, WU Jian, et al. Genetic analysis of soft soil structure and experiment on its influence engineering properties in Ningbo area[J].Industrial Construction, 2008, 38(3): 68－71.

[4]謝定義, 齊吉琳, 朱元林. 土的結構性參數及其與變形-強度的關系[J]. 水利學報, 1999, 10: 1－6.XIE Ding-yi, QI Ji-lin, ZHU Yuan-lin. Soil structure parameter and its relations to deformation and strength[J].Journal of Hydraulic Engineering, 1999, 10: 1－6.

[5]陳存禮, 胡再強, 高鵬. 原狀黃土的結構性及其與變形特性關系研究[J]. 巖土力學, 2006, 27(11): 1891－1896.CHEN Cun-li, HU Zai-qiang, GAO Peng. Research on relationship between structure and deformation property of intact loess[J]. Rock and Soil Mechanics, 2006,27(11): 1891－1896.

[6]駱亞生, 謝定義. 復雜應力條件下土的結構性本構關系[J]. 四川大學學報(工程科學版), 2005, 37(5): 14－18.LUO Ya-sheng, XIE Ding-yi. Structural constitutive relation of soils under complex stress conditions[J].Journal of Sichuan University (Engineering Science Edition), 2005, 37(5): 14－18.

[7]陳存禮, 高鵬, 何軍芳. 考慮結構性影響的原狀黃土等效線性模型[J]. 巖土工程學報, 2007, 29 (9): 1130－1136.CHEN Cun-li, GAO Peng, HE Jun-fang. Equivalent linear model of intact loess considering structural effect[J].Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1130－1136.

[8]劉恩龍, 沈珠江. 結構性土的強度準則[J]. 巖土工程學報, 2006, 28(10): 1248－1252.LIU En-long, SHEN Zhu-jiang. Strength criterion for structured soils[J]. Chinese Journal of Geotechnical Engineering , 2006, 28(10): 1248－1252.

[9]劉恩龍, 沈珠江. 結構性土的二元介質模型[J]. 水利學報, 2005, 36(4): 391－395.LIU En-long, SHEN Zhu-jiang. Binary medium model for structured soils[J]. Journal of Hydraulic Engineering,2005, 36(4): 391－395.

[10]楊振茂, 趙成剛, 王蘭民. 飽和黃土的液化的試驗研究[J]. 巖石力學與工程學報, 2005, 24(5): 864－871.YANG Zhen-mao, ZHAO Cheng-gang, WANG Lan-min.Testing study on saturated loess liquefaction[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(5): 864－871.