基于強度穩定綜合理論的加筋板極限強度分析

馮亮，佟福山

(哈爾濱工程大學船舶工程學院，黑龍江哈爾濱150001)

加筋板在船舶與海洋平臺等結構中被廣泛應用，其幾何結構與承壓性能均優于板和梁.長期以來，國內外的學者通過各種方法不斷研究其極限的承壓能力，希望得出簡便而準確的計算方法，來解決船舶設計師們的設計難題.

在探索解決結構極限強度問題的過程中，強度穩定綜合理論(combined theory of strength and stability，CTSS)在20 世紀80 年代由羅培林［1］提出.從文獻［1-7］來看，CTSS方法在梁柱和球殼的極限強度計算上已經有很好的應用，但對于其他結構的應用性如何還未得到證明.

本文用CTSS的方法來解決加筋板的極限強度問題，并將其結果與有限元法、規范和Paik經驗公式相比較，進而證明運用CTSS方法可以解決加筋板的極限強度問題.

1 船用鋼材HT32的特性

本文的研究是基于船用鋼材HT32.該材料特性參數［8］:彈性模量 E=206.01GPa，泊松比 v=0.3，比例極限 σp=190.512 MPa，屈服極限 σs=340.2 MPa(據文獻［9］該高強度鋼材的屈服極限名義值為315 MPa，平均值為340.2 MPa).由衍生比例定律可知［6-7］，材料的相對應力 -應變曲線和相對應力-切影應變曲線可用如下四參數冪函數方程來描述:

通過現代繪圖軟件Auto CAD的精確取值得出其相對應力應變曲線、切影應力應變曲線和切線模量因子曲線擬合后如圖1所示.圖中分別給出擬合數據的參數值，從剩余殘差平方和、相關系數的平方數值來看曲線擬合非常完美，說明衍生比例定律所提出的材料四參數冪函數的數學表達式在鋼材HT32上得到了體現.

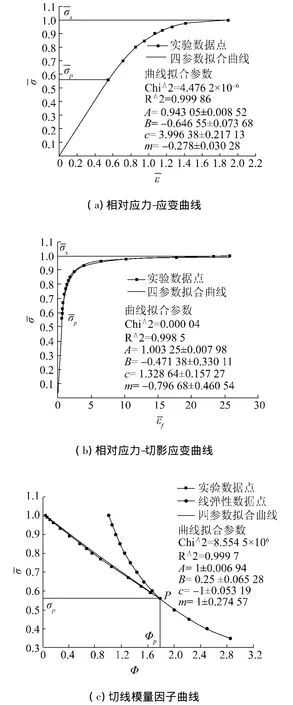
圖1 鋼材HT32響應曲線Fig.1 Response curves of steel HT32

2 CTSS對結構極限強度的求解方法

CTSS是以強度利用率函數即切線模量因子曲線方程來對結構極限強度問題進行求解的.它分為2個部分:1)通過采用材料的切線模量因子曲線來解決結構的物理非線性問題;2)通過采用結構的綜合因子n來解決結構由于橫向強度和初始缺陷所引起的幾何非線性問題.

以鋼材HT32為例，圖1(c)中以P點為界右邊的雙曲線部分表示結構處于線性階段屈曲，左邊表示結構處于非線性階段屈曲，很多鋼材在非線性階段近乎是一條直線，即c=-1，m=1，圖1(c)的非線性階段可用=1-0.25Φ代表可以得到保守且理想的效果.于是，其強度利用率函數近似可以表示為

對于一般的材料均可以用四參數方程統一:

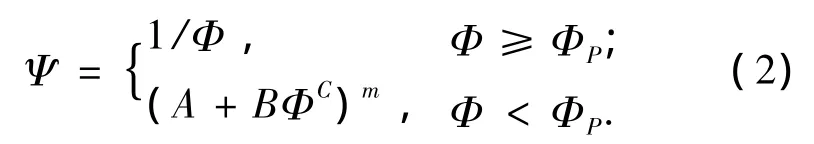
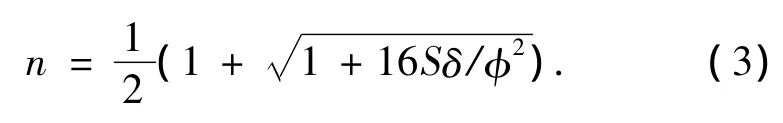
取n=1，即不考慮結構的橫向強度和初始缺陷的計算結果，代入方程(1)計算得

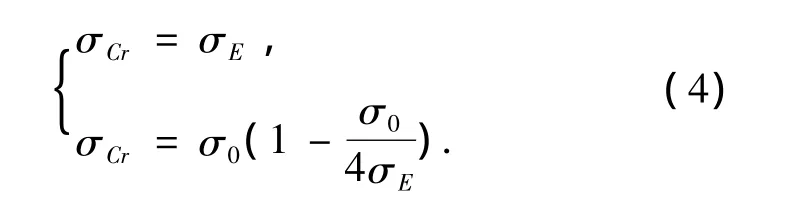
根據文獻［10］對船舶結構受壓時臨界應力σc做了如下規定:

式中:ReH為材料的屈服應力，N/mm2;σE為理想彈性屈服應力，N/mm2.

與方程(4)對比看出中國船級社對于結構屈曲的校核準則與CTSS的方法是同一的，只是出于保守的考慮用σ0/2代替σp作為彈性與非彈性的分界點.根據文獻［7］CT.3和鋼材HY-130的非線性階段近似于Ψ=1-0.2ΦP分別為0.77 和0.71.可以看出對于其他普通鋼材來說，按照CTSS的方法計算的結果能體現不同材料的不同特性，結果更加準確，而按照規范公式校核的結果更加偏于保守.

3 船用加筋板屈曲計算分析

3.1 加筋板的屈曲模式

加筋板受壓時通常有4種失效模式即:加強筋間板的失穩、加強筋的腹板的局部屈曲、加筋板結構的整體屈曲以及加筋板的梁柱失穩.其中第1種失效模式是由于加筋板有高強度的加強筋;而與此對應的第3種失效模式是由于加強筋尺度過小而產生的;第2種失效模式是由于加強筋腹板的高厚比較大而產生的;當加強筋和板的剛度相差不大時加筋板容易發生第4種失效模式.本文將按照以上4種屈服模式用CTSS的方法計算對應的極限強度，取最小者作為該加筋板實際的極限強度.

3.2 船體結構的結構系數

1)船體縱骨的結構系數.

根據文獻［10］無轉動的柱屈服模式，縱骨的理想彈性屈曲應力:

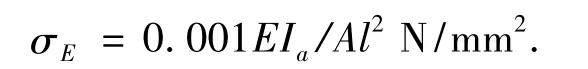
結構系數:

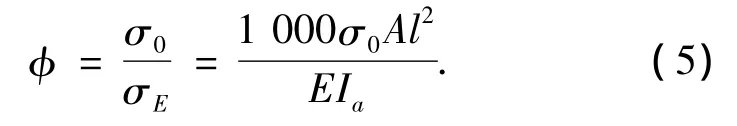
2)船體受壓板格理想(彈性)屈曲應力.

根據文獻［10］船體受壓板格理想彈性屈曲應力:

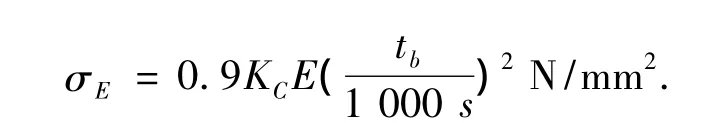
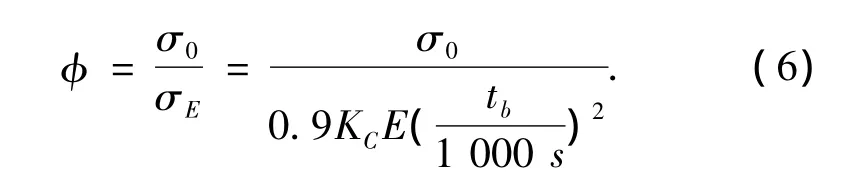
3)船體縱骨腹板理想(彈性)屈曲應力.

根據文獻［10］船體縱骨腹板理想彈性屈曲應力:

對于縱骨面板的要求:bf/tf≤15，即要求面板的寬度(對于T型材為面板的半寬)與面板厚度的比小于等于15.

結構系數:

4)加筋板整體理想(彈性)屈曲應力.

根據文獻［11］由能量法得出加筋板整體理想屈曲應力:

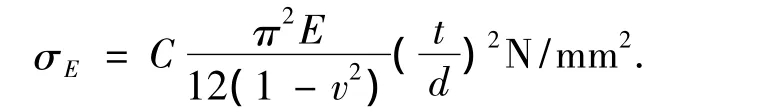
結構系數:

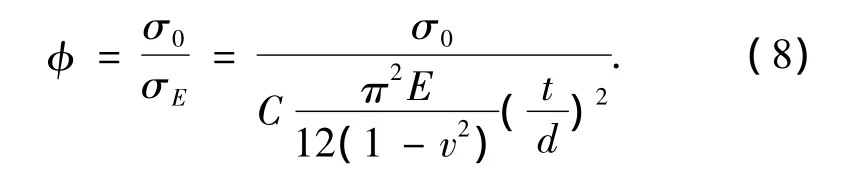
3.3 CTSS的計算實例與比較分析

表1是船舶中加筋板結構的典型尺寸，代表了一些的船舶結構樣式.

表1 7種典型船舶加筋板的尺寸Table 1 Seven kinds of typical sizes of stiffened panels

按照文獻［12］，經過巴普考維奇分析，可取帶板寬度be=0.44b.將船體結構各部分的結構系數算式(5)～(8)代入式(1)，在不考慮結構的橫向強度和初始缺陷情況下，即取綜合因子n=1時的計算結果如表2.

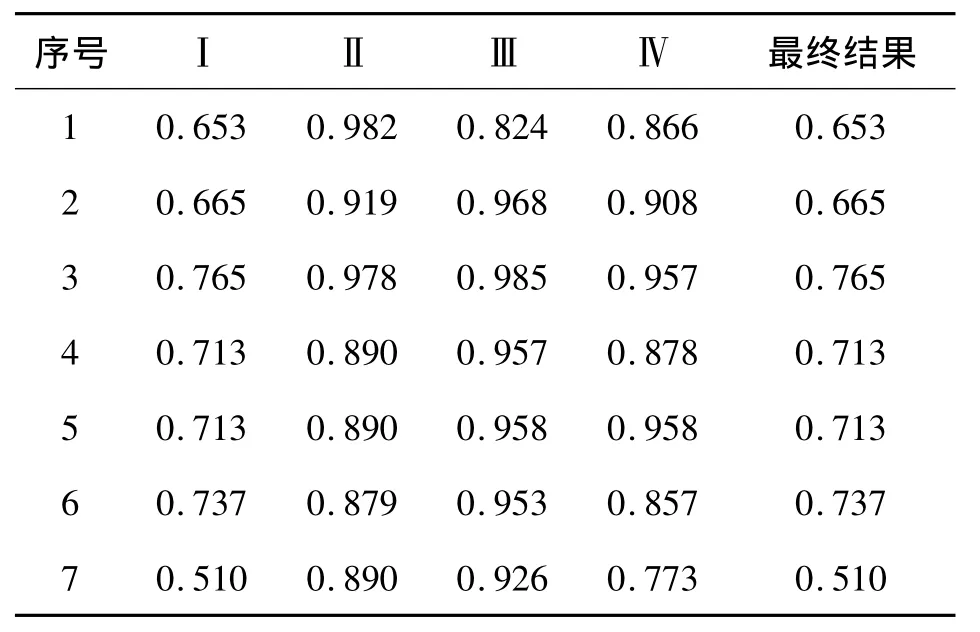
表2 CTSS計算結果Table 2 Calculation results of CTSS

如果按照文獻［10］中取be=b，根據計算得出這7組加筋板的第1種失效模式的數值將減少，但最終結果不變，這也體現了規范對板的有效寬度取值的保守性.

表2的結果與有限元和CCS的計算結果對比如表3.

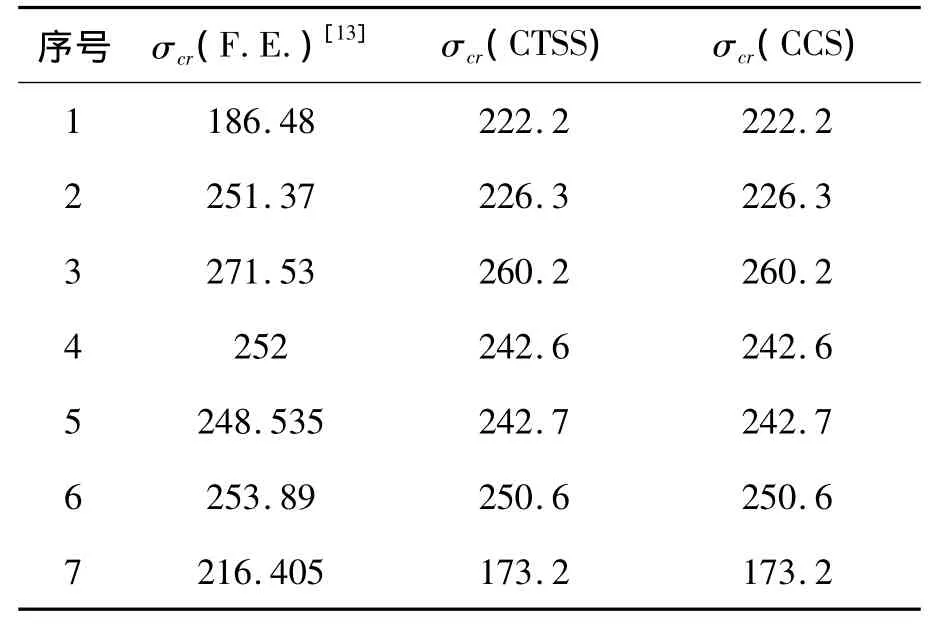
表3 加筋板極限強度計算結果比較Table 3 Comparison of calculation results MPa

從計算結果可以看出，幾種算法相差不超過10%.其中CTSS與CCS對于HT32這種鋼材的結構的計算結果相同，但對于其他材料CTSS可以給出與材料性能相符的計算結果，而CCS的計算結果更偏于安全.有限元法對計算復雜結構有著獨特的優勢，但相比CTSS，它的結果會隨著很多客觀因素變化，很不穩定.

3.4 含通常程度初始缺陷的加筋板極限強度的分析

Paik等［14］在130次有通常程度初始缺陷的加強筋破壞性試驗基礎上，提出受壓縮筋板格(鋼質)的極限強度經驗公式:

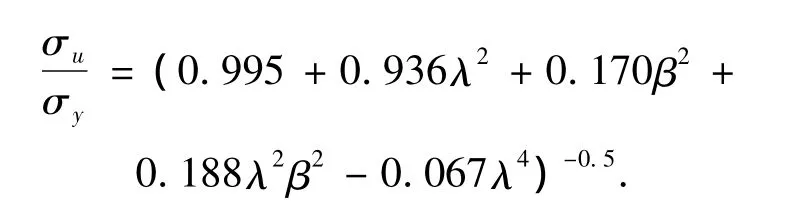
CTSS通過綜合因子n來修正橫向強度與初始缺陷對于結構極限強度的影響，表達式如式(3).對于通常程度的初始缺陷，取綜合因子n=1.15.修正后的結果與式(9)對比如表4.

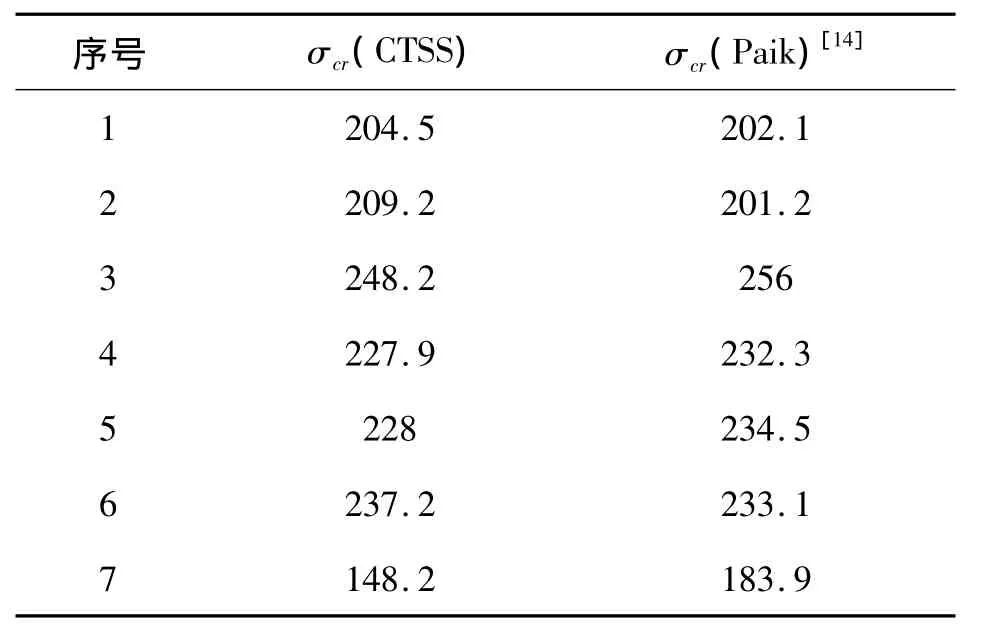
表4 含通常程度初始缺陷的加筋板極限強度計算結果比較Table 4 Comparison of calculation results with initial deflection MPa

由表4可知，前6組CTSS的計算方法與文獻［14］公式在計算結果上相差不超過4%，第7組差別相對較大是由于這2種算法對加筋板結構變化的敏感性不同所致.本文考慮了多種的失效模式，在結構的變化上更能體現優勢，所以可信度相比較高.

由于加筋板屬于組合結構，很多誤差在計算時會形成累積，所以上述方法在計算結果上有些偏差，但這幾種算法的趨勢是一致的，并且有很高的吻合程度.

4 結論

1)本文基于CTSS所提出的結構穩定性計算方法，對船舶加筋板結構進行計算分析，通過與有限元法，規范以及Paik經驗公式相比較，說明該方法適用于船舶加筋板結構的極限強度解算，拓展了CTSS方法的應用范圍.

2)通過與規范公式的整理比較，使得CTSS方法更具可信度，也從側面拓展了規范的應用范圍.

本文針對加筋板極限強度的計算只是CTSS方法應用上的拓展，缺少嚴密的理論推導是本文的不足之處，此工作還需力學工作者的進一步研究.

［1］羅培林.結構強度穩定綜合理論的梗概和意義［J］.機械強度，1986(5):56-61.LUO Peilin.Outline and significance for combined theory of strength and stability［J］.Journal of Mechanical Strength，1986(5):56-61.

［2］羅培林.應力應變六參數方程及其在結構穩定性的計算和實驗中的應用［J］.中國造船，1981(3):66-74.LUO Peilin.The stress-strain six parameters equation and its use in evaluating theoretically and experimentally the structural stability［J］.Shipbuilding of China，1981(3):66-74.

［3］羅培林.材料應力應變圖的相似性及其表達形式和應用［J］.哈爾濱船舶工程學院學報，1984(1):9-22.LUO Peilin.Application and expression forms of thematerial stress-strain similarity［J］.Journal of Harbin Shipbuilding Engineering Institute，1984(1):9-22.

［4］羅培林.用極限分析方法分析梁柱和球殼的穩定性［J］.哈爾濱船舶工程學院學報，1981(2):21-50.LUO Peilin.Stability analysis of columns and spherical shells by using limit analysismethod［J］.Journal of Harbin Shipbuilding Engineering Institute，1981(2):21-50.

［5］熊志新，佟福山.鈦合金深潛器耐壓球殼極限強度的切線模量因子算法［J］.哈爾濱工程大學學報，2010(2):178-181.XIONG Zhixin， TONG Fushan. Finding the ultimate strength of the titaniumalloy spherical pressure shell of a deep-sea submersible using the method of tangent modulus factor［J］.Journal of Harbin Engineering University，2010(2):178-181.

［6］羅培林.Hooke＇s Law(胡克定律)的革新與“強度穩定綜合理論”的創建和發展［J］.哈爾濱工程大學學報，2008，29(7):641-650.LUO Peilin.The establishment and development of a combined theory of strength and stability based on innovative Hooke＇s Law［J］.Journal of Harbin Engineering University，2008，29(7):641-650.

［7］張志平.廣義切線模量理論［D］.哈爾濱:哈爾濱工程大學，2005:11-44.ZHANG Zhiping.Generalized tangent modulus theory and its applications［D］.Harbin:Harbin Engineering University，2005:11-44.

［8］雒高龍，張淑茳，任慧龍.船用鋼應力-應變關系的數學表達及其在計算加筋板屈曲應力中的應用［J］.造船技術，2006(3):13-18.LUO Gaolong，ZHANG Shujiang，REN Huilong.Mathematical expression for stress-strain ofmarine steel and its application for beamcolumn buckling of stiffened plates［J］.Marine Technology，2006(3):13-18.

［9］束長庚，周國華.船舶結構的屈曲強度［M］.北京:國防工業出版社，2003:84-85.SHU Changgeng，ZHOU Guohua.Buckling strength of shipstructures［M］.Beijing:National Defense Industry Press，2003:84-85.

［10］中國船級社.鋼質海船入籍規范［M］.北京:人民交通出版社，2009:59-61.China Classification Society.Steel shipcitizenshipnorms［M］.Beijing:People＇s Traffic Publishing House，2009:59-61.

［11］李衛華.板架結構穩定性綜合分析及其計算程序系統的研制［D］.武漢:武漢理工大學，2002:81.LIWeihua.A synthesis analysis of stability of structures of grillage and the design of its programsystem［D］.Wuhan:Wuhan University of Technology，2002:81.

［12］陳鐵云，陳伯真.船舶結構力學［M］.北京:國防工業出版社，1984:287-289.CHEN Tieyun，CHEN Bozhen.Structual Mechanics for Ships［M］.Beijing:National Defence Industrial Press，1984:287-289.

［13］ZHANG Shengming，IMTAZ K.Buckling and ultimate capability of plates and stiffened panels in axial compression［J］.Marine Structures，2009(22):791-808.

［14］PAIK JK，THAYAMBALLIA K，KImB J.Advanced ultimate strength formulations of shipplating under combined biaxial compression/tension，edge shear，and lateral pressure loads［J］.Marine Technology，2001，38(1):9-25.