拉壓性能不同鋼箱梁的純彎曲彈塑性分析

劉偉龍

工程中常用的一些金屬材料，它們的拉伸與壓縮性能存在差異，即所謂的“S-D效應(yīng)”[1］。在過(guò)去的工程實(shí)踐中，人們認(rèn)為材料是拉壓同性的，按Mises準(zhǔn)則或Tresca準(zhǔn)則對(duì)塑性材料進(jìn)行彈塑性分析時(shí)往往不考慮拉壓性能的不同[2］。

近年來(lái)，考慮材料拉壓性能不同的強(qiáng)度分析，在國(guó)內(nèi)外文獻(xiàn)中開(kāi)始引起關(guān)注[3-6］。本文為了便于工程計(jì)算與應(yīng)用，在研究鋼箱梁的彈塑性性能時(shí)，將鋼箱梁的材料本構(gòu)關(guān)系簡(jiǎn)化成拉壓屈服極限不同的理想彈塑性模型，對(duì)彈塑性發(fā)展全過(guò)程進(jìn)行研究，得到了依賴(lài)于拉壓比γ的彈性、塑性極限彎矩的計(jì)算公式以及彎矩與曲率之間的關(guān)系。通過(guò)幾何參數(shù)變化，這些公式還適用于槽形、∏形等鋼梁的彈塑性分析。

1 彈性、塑性極限彎矩

鋼箱梁截面幾何尺寸如圖1所示。當(dāng)整個(gè)截面處于彈性狀態(tài)時(shí)，橫截面上的正應(yīng)力分布如圖2a)所示。圖2a)中σst表示材料鋼材的拉伸屈服極限。

當(dāng)截面上的拉應(yīng)力達(dá)到σst時(shí)，彈性極限彎矩為:

當(dāng)M＞Me時(shí)，中性軸偏離形心，偏離距離為e，如圖2b)所示。圖2b)中σst表示材料鋼材的壓縮屈服極限，令γ=σst/σsc≤1。這一階段梁的受拉層纖維的應(yīng)變繼續(xù)增大，應(yīng)力值保持為σst，塑性區(qū)逐步擴(kuò)大。當(dāng)受壓層纖維的最大壓應(yīng)力達(dá)到σsc時(shí)，受壓層纖維也逐漸進(jìn)入塑性狀態(tài)。根據(jù)如圖2c)所示應(yīng)力分布圖，建立靜力平衡條件，即:

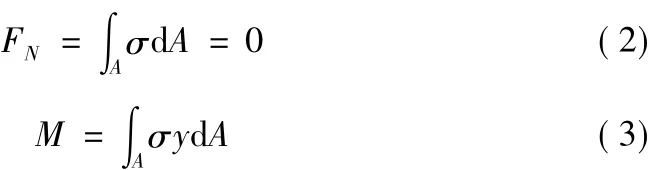
整理可得:

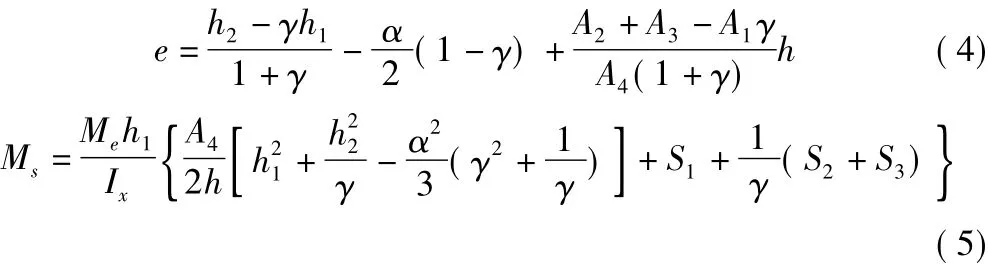
其中，Ai，Si分別為底板、頂板及兩懸臂板的面積和凈距，i=1，2，3;A4為兩腹板的面積;Ix為截面的慣性矩。在式(5)的推導(dǎo)過(guò)程中，考慮到偏心距是一個(gè)較小的量，略去了含有e2，e/h及e/h1的項(xiàng)。

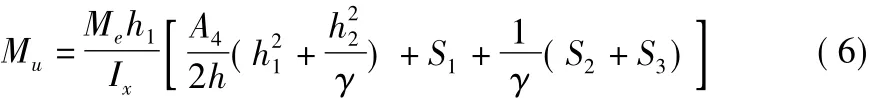
2 彎矩—曲率的關(guān)系

當(dāng)M≤Me時(shí)，材料處于彈性狀態(tài)，彎矩與曲率成正比，即:

其中，E為材料的彈性模量。

當(dāng)M＞Me時(shí)，材料逐漸進(jìn)入彈塑性狀態(tài)，由如圖2c)所示的幾何關(guān)系可知:

進(jìn)一步聯(lián)立式(1)，式(7)以及式(8)，可得:

將式(9)代入式(7)消去α，得到彎矩與曲率之間的關(guān)系:

3 數(shù)值結(jié)果與幾何參數(shù)分析

1)鋼箱梁橫截面幾何尺寸為 h=250 cm，b1=b2=b3=240 cm，t1=35 cm，t2=t3=25 cm，t4=30 cm，材料抗拉屈服極限σst=300 MPa，彈性模量 E=2.0 ×105MPa。取 γ =σst/σsc=0.75時(shí)，計(jì)算可得 e為 h的7.2%，Mu/Me=1.394，塑性極限彎矩為2.078×106kN·m。與材料的σst和σsc相等的情況相比較，塑性極限彎矩提高16.67%。顯然考慮材料的拉壓性能不同能更充分地發(fā)揮材料的潛力。

2)參數(shù)分析。

表1 塑性極限彎矩的參數(shù)分析

如表1所示，本文得到的彈性極限彎矩計(jì)算公式、塑性極限彎矩計(jì)算公式以及彈塑性階段的彎矩與曲率之間的關(guān)系經(jīng)過(guò)一定的參數(shù)變化，還適用于∏形、槽形、矩形等鋼梁的分析。例如，取t1=t2=t3=0，則如圖1所示箱梁截面轉(zhuǎn)化為寬為B=2t4、高為h的矩形截面。由式(1)，式(6)化簡(jiǎn)可得:彈塑性階段的彎矩與曲率之間的關(guān)系為

3)進(jìn)一步令γ=1，上述公式還可以進(jìn)一步蛻化到σst與σsc相等時(shí)的一般情況。

4 結(jié)語(yǔ)

本文對(duì)純彎曲狀態(tài)下的鋼箱梁進(jìn)行彈塑性極限分析，得到了依賴(lài)于拉壓比γ的彈性極限、塑性極限彎矩計(jì)算公式。通過(guò)一定的幾何參數(shù)變化，這些公式同樣適用于∏形、槽形、矩形等鋼梁的彈塑性分析。令γ=1，所得公式可進(jìn)一步用于拉壓性能相同時(shí)鋼箱梁彈性極限彎矩與塑性極限彎矩的求解。由數(shù)值分析結(jié)果可知，考慮材料拉壓性能不同時(shí)，鋼箱梁的塑性極限彎矩比不考慮拉壓強(qiáng)度不同時(shí)的塑性極限彎矩有所提高，充分地發(fā)揮了材料的潛力。而以往采用材料拉壓性能近似相同的假設(shè)，對(duì)塑性材料進(jìn)行彈塑性分析是保守可行的。

[1]Theocaris PS.A general yield criterion for engineering materials[J］.Depending on Void Growth Mechanics，1986(21):97-105.

[2]范欽珊.材料力學(xué)[M］.北京:高等教育出版社，2000.

[3]呂桂英.拉壓性能不同金屬材料的非經(jīng)典塑性本構(gòu)理論及實(shí)驗(yàn)研究[D］.哈爾濱:哈爾濱工業(yè)大學(xué)博士學(xué)位論文，1987.

[4]龐寶君，張澤華.拉壓性能不同材料厚壁圓筒與厚壁球殼的極限分析[J］.力學(xué)與實(shí)踐，1996，18(1):92-95.

[5]馮西橋，劉信聲.拉壓性能不同對(duì)厚壁圓筒安定性的影響[J］.力學(xué)與實(shí)踐，1995，17(5):28-30.

[6]馬景槐.拉壓異性強(qiáng)化材料高壓容器的自增強(qiáng)分析[J］.石油化工設(shè)備，2001，30(1):1-4.