基于能量耗散的混凝土單軸受拉損傷模型
唐仁忠 劉鳳麗 孫從亞
0 引言
當前的結構設計是以強度的極限承載力為基礎的,實際工程中混凝土構件裂縫的形成大多是由于材料的拉應力或拉應變達到相應的極限值而引起的,因此對混凝土的受拉進行研究不但具有一定的理論意義,而且有重要的實際價值。
混凝土的破壞基本原理是微開裂,也即微裂縫的形成、擴展、貫通的過程,這一過程反映了混凝土的力學性能和應力—應變關系的響應,因此用損傷理論分析混凝土的破壞過程是合適的。國內外學者利用損傷理論對混凝土的損傷行為作了大量工作,提出了一些有效的混凝土損傷模型[1],國外的有Kachanov損傷模型、Loland受拉損傷模型、Mazars損傷模型等;國內主要有分段線性模型和分段曲線模型等。
混凝土是一種單軸抗壓強度遠大于抗拉強度的材料,在單軸受拉狀態下近似彈脆性材料。因此,本文基于Najar損傷理論[2],從量耗散的角度提出一種由高斯積分算法計算損傷的混凝土單軸受拉損傷模型。
1 損傷模型
從熱力學角度看,損傷變量表示物質內部結構的不可逆的變化過程,因此是一種內變量,用這種內變量來描述損傷的演變發展。借助Kachanov的“連續度”的概念,連續介質損傷力學將材料的損傷描述為有效受力面積的減少,于是經典損傷變量被抽象為:
其中,A為材料受損前的截面面積;ˉA為受損后的有效受力面積;D=0為無損狀態;D=1為完全破損狀態。
基于Najar損傷理論的損傷變量定義為:
其中,W0為無損狀態應變能密度,W0=E0·ε2/2;Wε為損傷狀態下的應變能密度,Wε=σ·ε/2,σ,ε分別為損傷狀態對應的應力和應變。對于式(2),當Wε=W0,D=0;當 Wε?W0,D→1;當0 <Wε<W0,0<D<1,故用式(2)描述混凝土的損傷發展是合理的。
在Najar損傷理論中,損傷狀態的應變能按線性求得,即Wε=σ·ε/2,圖1中陰影部分,其顯然要比實際的小,從而由其計算得的損傷就要比實際的大。損傷狀態下應變能的計算精確與否直接關系到損傷逼近真實的程度。文獻[3]從能量耗散角度提出分段線性損傷模型;文獻[4]用辛普生積分法從能量耗散角度研究損傷,模型都較Najar線性方法有所提高。辛普生積分法較分段線性法精度有所提高,但辛普生積分法只適用于積分區域端點在內的積分點等間距分布,因此對積分點的選取有所限制;同時對于n個積分點,辛普生積分法的精度為n-1。因此本文提出應用高斯積分法計算損傷狀態下的應變能,高斯積分算法適用于積分點不等間距的情況,更重要的是在n個積分點上,高斯積分算法的精度可以達到2n-1次,這樣在相同的積分點數情況下可以更好的逼近實際值,從而用其計算損傷狀態下的應變能更精確,損傷更接近真實損傷。
若將待積分應變區間分成N個小區間,對每個小區間應用高斯積分法,將在每個小區間算得的應變能求和就得能到整個損傷狀態的應變能密度:

將式(3)代入式(2)可得:
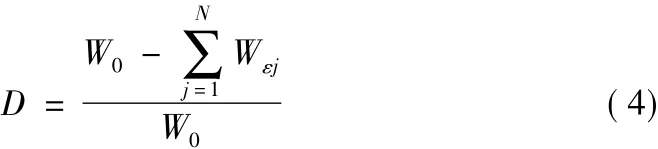
由上式對已知的單軸受壓的應力—應變關系,在劃分的足夠小的應變區間上,編制計算機程序就可得到損傷隨應變的變化規律,進而可以直觀地描述混凝土的損傷演變過程。
2 損傷模型驗證
選取GB 50010-2002混凝土結構設計規范推薦的單軸受拉應力—應變關系式[5]:
當x≤1時:

當x>1時:

其中,x=ε/εt,εt為與 ft對應的峰值應變,y= σ/ft,ft為混凝土單軸抗拉強度;at為單軸受拉應力—應變關系曲線下降段參數,具體可以查閱GB 50010-2002混凝土結構設計規范中表C.2.2。
由圖2可知,除Loland模型[6]接近直線外,其余模型都是外凸的,損傷演化趨勢是一致的;從圖形的走勢來看,Mazars模型[7]最陡,損傷演化得相對最快,Loland模型演化得相對最慢,而本文模型介于分段曲線與分段線性模型二者之間且比較平緩光滑,因此應用Mazars模型和分段線性模型描述高強度脆性混凝土受拉損傷演化較為合適,Loland模型可用以描述低強度混凝土的損傷演化,本文模型與分段曲線模型比較適合描述中強度混凝土的損傷演化。
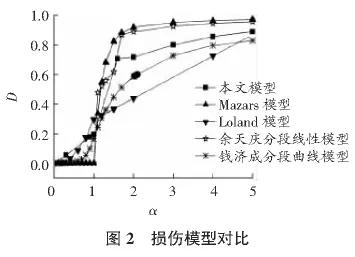
本文模型在初始段估計的損傷值偏大,這在一定程度上與本模型從開始加載就考慮損傷的發展有關,從損傷曲線的形狀可知本文基于能量耗散理論建立的損傷模型是合理的。
3 結語
通過與已有單軸受拉損傷模型的對比可以得出:本文基于Najar損傷理論,從能量耗散的角度提出的混凝土單軸受拉損傷模型是合理的,模型能夠合理的解釋混凝土的損傷發展。模型采用了高斯積分算法計算損傷,結果的精度相對更精確。但是,模型只選取了強度為C30的混凝土進行了理論驗證,應該從試驗和實際應用的角度對模型的有效性做進一步驗證。
[1]董毓利.混凝土非線性力學基礎[M].北京:中國建筑工業出版社,1997.
[2]Krajcinovic D,Lemaitre J.Continuum damage mechanics theory and applications[M].New York:Springer Verilag,1987:233-294.
[3]趙 雷,陳 虬.混凝土構件的一種新分段線性損傷模型[J].重慶交通學院學報,1996,15(1):27-33.
[4]王中強,于志武.基于能量損失的混凝土損傷模型[J].建筑材料學報,2004,7(4):365-369.
[5]GB 50010-2002,混凝土結構設計規范[S].
[6]Loland K E.Continuous Damage Model for Load-response Estimation of Concrete[J].Cement and Concrete Research.Pergamon Press,1980,1(10):395-402.
[7]Mazars J.Continuous Damage Theory-Applicationto Concrete[J].Journal of Engineering,1980,115(2):345-365.

